可变生成多项式与输入位宽的并行CRC

张 强

(思科系统(中国)研发有限公司,上海200233)

可变生成多项式与输入位宽的并行CRC

张 强

(思科系统(中国)研发有限公司,上海200233)

介绍了两种LFSR类型的CRC且比较了它们的特性,然后以II型LFSR为基础,分两步先后推导出任意m比特的直接并行计算以及如何进行连续m比特的计算,即得到可变生成多项式与输入位宽的并行CRC算法,最后举例给出基于CCITT-16协议的4比特输入位宽的VHDL程序实现代码并给出仿真验证结果。由此对于给定的生成多项式与输入位宽,通过提出的算法用C语言或者硬件电路描述语言可以实现快速简单的并行CRC计算。

循环冗余校验 线性反馈移位寄存器 并行算法

0 引 言

CRC全称为Cyclic Redundancy Check,中文名称为循环冗余校验,由W.Wesley Peterson于1961年发明,编码和解码方法简单,检错能力强,在通信领域广泛地用于实现差错控制,例如发送端根据传送的m位二进制码序列,用一定的规则产生一个校验用的r位监督码(CRC码),附在原始信息后面,构成一个新的二进制码序列共m+r位,然后发送出去。接收端根据信息码和CRC码之间所遵循的生成规则进行校验,以确定传送中是否出错[1]。这个规则,在差错控制理论中称为生成多项式。

随着高带宽数据处理与数据传输的发展,串行CRC早已不能满足现代通信系统的需求,因此高阶次生成多项式与高输入位宽的并行CRC被广泛使用,目前主要有查表法[2]和并行矩阵法[3]。查表法虽可实现快速CRC计算,但需消耗硬件电路中宝贵的存储资源,甚至是不能实现的,例如对输入位宽为32比特的数据做CRC-32的并行查表计算,需要消耗的存储资源为232×32比特,即16G字节的存储空间。而并行矩阵法可以用简单的异或逻辑快速实现并行CRC,但目前流行的算法中多以2的幂次输入位宽进行推导,比如8、16和32,且多项式幂次也为偶数。文中将对任意多项式阶次与任意输入位宽的并行矩阵法进行推导。

1 串行算法

1.1 多项式除法

对于信息串“11100110”,设信息多项式为M(x)=x7+x6+x5+x2+x1。若生成多项式G(x)=x3+ x1+1,则M(x)×x3除以G(x)的余数项R(x)={M(x)×x3}mod{G(x)}=x2,即CRC码为“100”。对于多项式除法的逻辑实现,需要将多项式除法和电路模型对应以方便实现CRC计算。线性反馈移位寄存器(LFSR)是很好的电路模型[4]。

1.2 LFSRI型

LFSR由r个D触发器和异或门以及一个反馈电路组成,其中r为生成多项式的最高阶次。如图1所示,I型中系数Gi(i=0,1,…,r-1)决定Yr-1是否作为反馈参与寄存器Yi-1和输入串行比特D的异或运算。

图1 I型线性反馈移位寄存器Fig.1 LFSR I

1.3 LFSR II型

由系数Gi决定输入D与Yr-1的异或结果是否作为反馈参与寄存器Yi-1的异或运算。

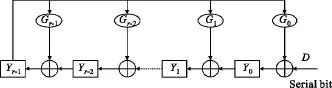
图2 II型线性反馈移位寄存器Fig.2 LFSRII

1.4 类型比较

I型与II型对比如表1所示。

表1 I型与II型对比Table 1 Comparison of between type I and II

2 并行CRC算法

2.1 m个比特的并行计算

设m位比特串B={Dm-1,Dm-2,…,D1,D0},生成多项式系数G={Gr-1,Gr-2,…,G1,G0},则余数项R(x)={B×xr}mod{G(x)}={(Dm-1×xm-1+Dm-2×xm-2+,…,D1×x1+D0)×xr}mod{G(x)}。令Ri={Di×xi× xr}mod{G(x)}且0≤i≤m-1,即Ri等于比特串{Di,左移r位后除以G的余数项,则总的余数项为,由II型LFSR可知Ri需i+1次的移位运算,令j为移位运算的次序且1≤j≤i+1,则Ri,j,r为Ri经过j次移位后第r位比特的结果,通过II型的电路计算可得:

由Ri,1和Ri,j可知,Di首先进入II型电路,后续对进入‘0’的运算,都是将Yr-1中的结果不断的对电路做式(2)中的线性反馈异或运算[5]。因Ri,1中的每一比特均有Di乘数因子,所以最终的Ri,i+1中的每一比特必有Di因子和一个由多项式系数经过运算得出的系数因子Hi,r,则Ri表示为:

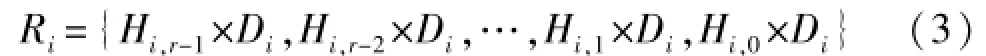
考察式(3),若Di=0,则Ri=0,若Di=1,则

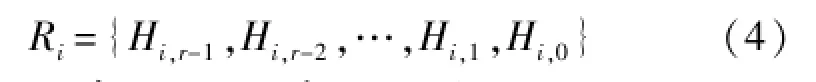
由式(1)知,Di=1时,Ri,1={Gr-1,Gr-2,…,G1,G0}；因系数Gi为常数,所以将Ri,1代入式(2),通过循环迭代,得到Ri,i+1,即Ri。从式(4)可见,Hi,r已求出,则Ri最终由变量Di确定。

将式(2)迭代中的每个结果保存,得到m个Hi={Hi,r-1,Hi,r-2,…,Hi,1,Hi,0}；则

由式(5)可知,H矩阵为已知,将任意m位比特串B={Dm-1,Dm-2,…,D1,D0}输入,通过矩阵运算可立即得到CRC结果R。

2.2 连续m个比特的并行计算

对于连续的并行输入,需对连续的前后两次m比特并行计算进行分析,才能达到连续处理并行数据的目的。

设B[n]为并行数据中的第n个m位比特串,生成多项式G的次数为r,设Br[n]为B[n]除以G的余数,即Br[n]=(B[n]×xr)mod(G)。

则n个m位比特除以G的余数为:

算法为:

a)用2.1节的算法快速计算得出B[n-1]的余数Br[n-1]。

b)将Br[n-1]与B[n-2]异或。

c)异或后的结果重复a)中的快速计算。

2)若r＜m,则

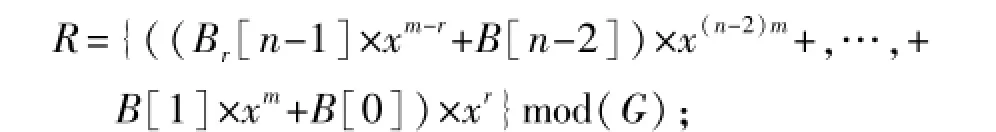
算法为:

a)用2.1节的算法快速计算得出B[n-1]的余数Br[n-1]。

b)将Br[n-1]左移m-r位且右边补‘0’后与B [n-2]异或。

c)异或后的结果重复作a)中的快速计算。

3)若r＞m,则

令Brm[n]为Br[n]的高m位,Br-m[n]为Br[n]的低r-m位,即

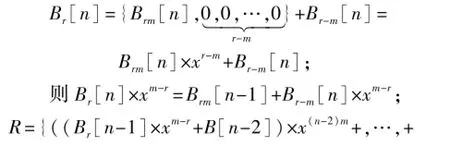
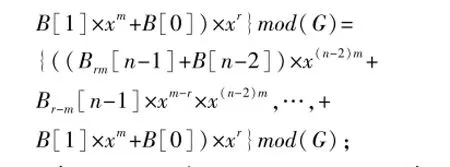
令B′r[n-2]为Brm[n-1]+B[n-2]除以G的余数,类似B[n-1]项的计算,得

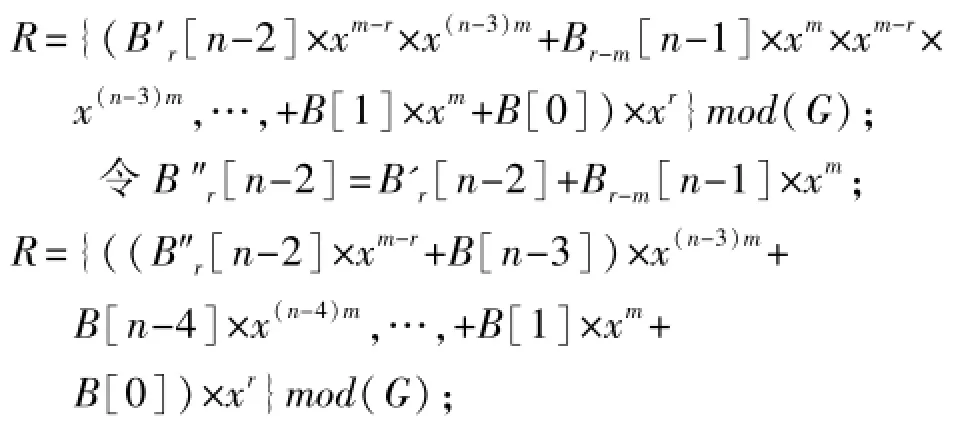
可见R中的最高阶次为(n-3)m,与计算B[n-1]项后相比阶次降低了1。

a)用2.1节的算法快速计算得出B[n-1]的余数Br[n-1]。

b)Brm[n-1]与B[n-2]异或后重复做a)中的计算得B′r[n-2]。

c)B′r[n-2]与{Br-m[n-1],异或得B″r[n-2]。

d)对B″r[n-2]和B[n-3]重复做b)中的计算。

3 VHDL设计举例

对CCITT-16标准,其生成多项式G(x)=x16+ x12+x5+1,输入位宽4 bit,VHDL实现代码为:

4 仿真验证

将十进制数据串“0123456789”转换成十六进制的ASCII码值,即“0x30313233343536373839”,然后每个时钟周期将上述结果中的数据以4 bit为单位从左端依次赋值给变量D,令Y初值为0。如图3所示,仿真最终的结果为0x9C58。

图3 CCITT-16协议的4 bit输入位宽CRC仿真Fig.3 CRC simulation for 4 bit data with CCITT-16

5 结 语

文中给出可变生成多项式与输入位宽的并行CRC算法,只需将生成多项式系数G代入公式即可得系数矩阵H,每组输入比特向量与矩阵相乘可得CRC计算结果；对连续的并行计算,须根据2.2节中的三种情况进行判断,把前次的结果与下次的输入比特关联运算,所得结果才能作为下一次CRC运算的输入。由此实现连续并行计算的一种通用算法。可见,与通常的并行CRC算法相比,文中不对多项式阶次与输入位宽做约束,只需将使用的多项式阶次与输入位宽作为参数,即可运用文中的算法快速得到并行CRC的逻辑运算电路。

[1] 刘伟,王俊芳,王立莹,等.千兆以太网MAC中CRC算法的设计与实现[J].通信技术,2012,45(07):32-34,37.

LIU Wei,WANG Jun-fang,WANG Li-ying,et al.CRC Algorithm Design and Develop ment in Gigabit Ethernet-MAC[J].Communications Technology,2012,45(07):32 -34,37.

[2] 李剑锋.新的高性能CRC查表算法[J].计算机应用, 2011(06):181-182,121.

LI Jian-feng.New Table Look-up Algorithm for High-Performance CRC[J].Computer Application,2011(06): 181-182,121.

[3] CAMPOBELLO G,PATANE G,RUSSO M.Parallel CRC Realization[J].IEEE Transaction on Computers,2003, 52(10):1312-1319.

[4] 王新梅,肖国镇.纠错码-原理与方法[M].西安:西安电子科技大学出版社,2001.

WANG Xin-mei,XIAO Guo-zhen.Correcting Code-Theory and Method[M].Xi′an:Xi′an University of E-lectronic Science and Technology Press,2001.

[5] PEREZ A.Byte-Wise CRC Calculation[J].IEEE Micro, 1983,N(06):40-50.

ZHANG Qiang(1978-),male,M.Sci., senior hardware engineer,majoring in FPGA algorithm research and development in communication system.

Parallel CRC Algorithm with Variable Generator and Data Width

ZHANG Qiang
(Cisco Systems China R&D Center,Shanghai 200233,China)

The paper describes two methods of LFSR and compares their features.Then based on type II of LFSR,it derives in two steps the calculation of‘m’bits parallel data in one clock cycle and the execution of continuous parallel calculation.So the whole algorithm for variable generator and data width can be realized.Finally,an example based on CCITT-16 and 4 bit data width is provided by using VHDL,and the simulation result also given.Therefore for certain generator and data width,parallel CRC could be completed quickly and easily by C or hardware description language.

CRC；LFSR；parallel algorithm

TN918

A

1002-0802(2014)03-0335-04

10.3969/j.issn.1002-0802.2014.03.020

张 强(1978—),男,硕士,高级硬件工程师,主要研究方向为通信系统中FPGA实现算法的研究与开发。