基于DFT变换的彩色图像平滑滤波

汤全武，史崇升，吴 佳

（宁夏大学物理电气信息学院，宁夏银川750021）

0 引 言

常见的图像平滑的方法可以归纳为以下几类方法:邻域平均法、多图平均法、中值滤波法和频域低通滤波法等［1，2］，而这些方法主要是针对二维的灰度图像进行处理，即使涉及到彩色图像的平滑，通常也是将彩色图像转化成灰度图像，再利用上述方法实现平滑滤波，或者利用imfilter函数，采用线性空间滤波器对RGB图像或HSI图像的亮度分量进行平滑滤波，专门用于彩色图像的平滑滤波方法研究的比较少。文献［3］根据人眼视觉系统的空间模糊特性、人眼视觉感知中的彩色细节失明及同时对比特性出发，确定初始高斯模板和高斯权值矩阵，实现对图像的平滑；文献［4－7］等通过选择不同的全局固定带宽或者局部自适应带宽，将Mean Shift算法运用于图像的平滑与分割中，文献［8］在此工作基础上之上，又根据图像颜色分布的丰富程度定义了自适应空域带宽，并利用最小化局部方差函数和最大化频域结构相似度函数获得自适应值域带宽，通过定义采样点权重，克服了图像过平滑问题，取得了较好的结果；文献［9］基于HSI彩色空间对图像进行平滑，能够有效消除图像噪声影响和改进图像质量。在上述彩色图像平滑方法中，有采用空间滤波，将Mean Shift算法应用于彩色图像平滑，将RGB图像转换到其他彩色空间并对图像进行平滑处理，但并未涉及到利用频域滤波方法对图像进行平滑。因此，本文提出了一种新的彩色图像平滑滤波的方法，即DFT平滑滤波算法。

1 彩色图像的离散傅里叶变换

一幅彩色图像就是彩色像素的一个M×N×3数组，其中每一个彩色像素点都是在特定空间位置的彩色图像相对应的3个分量，可以看成是一个由3幅灰度图像形成的“堆”。频域滤波方法只能对二维图像进行滤波，不能直接对彩色图像进行处理，但若将彩色图像的各分量进行提取，其分量图像均为M×N的数组，则可对彩色图像进行频域滤波［10］。

令f（x，y）表示一幅M×N×3彩色图像的分量，其中x＝0，1，2，…，M－1和y＝0，1，2，…，N－1。f（x，y）的二维离散傅里叶变换可表示为

其中，μ＝0，1，2，…，M－1和ν＝0，1，2，…，N－1。

设给定h（h，y）表示一个M×N的函数，其中h＝0，1，2，…，M－1和y＝0，1，2，…，N－1。h（h，y）的二维离散傅里叶变换可表示为

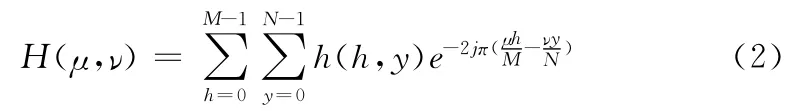
其中，μ＝0，1，2，…，M－1和ν＝0，1，2，…，N－1。这里，我们通常将H（μ，ν）称为滤波传递函数。

空间域和频域线性滤波的基础都是卷积定理，该定理可以写为

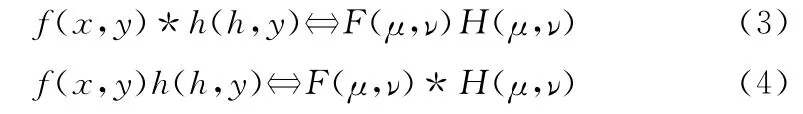
其中，符号“＊”表示两个函数的卷积，双箭头两边的表达式组成了傅里叶变换对。在滤波的问题上，通常采用式（3），则f（x，y）滤波图像f1（x，y）可表示为

其f1（x，y）对应的二维傅里叶变换为

将式（6）带入到式（5）中，并结合式（1）和式（2）可得滤波图像f1（x，y）的表达式为

至此，完成了对彩色图像分量f（x，y）的频域滤波，将彩色图像的其他分量分别进行频域滤波，再将分量滤波图像用cat函数级联，即可实现彩色图像的平滑滤波。

2 DFT平滑滤波算法的设计

2.1 基本思想

令Sxy表示彩色图像中以（x，y）为中心的邻域的一组坐标。在该邻域中，彩色图像向量的平均值为

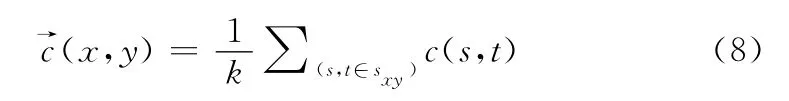
其中，k是邻域中像素的数量。同时，它也遵从

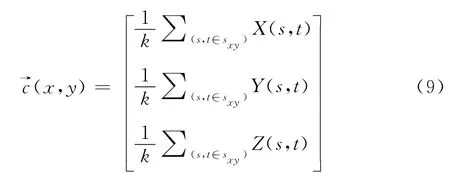
其中，X、Y、Z分别表示Sxy在（x，y）的3个分量。对比式（8）和式（9），我们可以得到这样的结论:用邻域平均的平滑可以在每个图像平面的基础上执行。如果邻域平均直接在彩色向量空间执行，那么结果是相同的。彩色图像是三维空间图像，不能直接进行频域滤波，但根据以上结论，我们可以对彩色图像的各分量分别进行频域滤波。因为其分量图像是二维图像，对分量图像进行DFT离散傅里叶变换，并利用卷积定理，即式（3）可实现分量图像在频域的滤波，将滤波的分量图像进行离散傅里叶逆变换，可转换至对应分量图像的平面。再将各分量的滤波图像利用cat函数进行合成，则可实现使用频域滤波器平滑彩色图像的方法。

2.2 算法的实现

该算法首先提取彩色图像的各分量，若待平滑的图像为RGB图像，提取的分量分别为红、绿、蓝分量图像；若要从非RGB彩色空间对图像进行平滑，就使用相应的转换函数将RGB图像转为其他空间的彩色图像，再提取图像的分量图像。然后分别对每幅分量图像进行DFT频域滤波，其中滤波器是利用fspecial函数产生的大小为16×16像素的‘average’滤波器。最后将各分量的滤波图像进行合成。具体实现算法的流程框图如图1所示。

图1 DFT平滑滤波流程

DFT平滑滤波算法的核心功能编程如下:

clear all

clc

fc＝imread（′bld.tif′）；%读入RGB图像

w＝fspecial（′average′，16）；%产生尺寸大小为16×16像素的‘average’滤波器

%RGB图像各分量的提取

fR＝fc（:，:，1）；

fG＝fc（:，:，2）；

f B＝fc（:，:，3）；

%将RGB各分量归一化

f R＝mat2gray（f R）；

fG＝mat2gray（fG）；

fB＝mat2gray（fB）；

%获取各分量的填充参数

PQR＝paddedsize（size（f R））；

PQG＝paddedsize（size（f G））；

PQB＝paddedsize（size（fB））；

%生成对各分量进行滤波的频域滤波器

HR＝freqz2（w，PQR（1），PQR（2））；

HG＝freqz2（w，PQG（1），PQG（2））；

HB＝freqz2（w，PQB（1），PQB（2））；

%将各分量的频域滤波器中心频率移到四个角

WR＝ifftshift（HR）；

WG＝ifftshift（HG）；

WB＝ifftshift（HB）；

%对RGB各分量图像进行频域滤波

ffR＿filtered＝dftfilt（f R，WR）；%对R分量

ffG＿filtered＝dftfilt（fG，WG）；%对G分量

ffB＿filtered＝dftfilt（fB，WB）；%对B分量

%RGB各分量滤波图像的合成；

f RGB＿filtered＝cat（3，ffR＿filtered，ffG＿filtered，ffB＿filtered）

其中，paddedsize和dftfilt函数是自定义函数。paddedsize函数的功能为:假设函数f（x，y）和g（x，y）的大小分别为A×B和C×D，通过对f和g补零，用于计算满足等式P≥A＋C－1和Q≥B＋D－1的最小偶数值；dftfilt函数实现频域滤波。

2.3 评价标准

本文采用均方误差（MSE）、峰值信噪比（PSNR）值和相关测度K［11］作为平滑彩色图像结果的客观评价标准。

均方误差MSE用来表示滤波图像与原始图像之差平方的期望值，其离散形式为

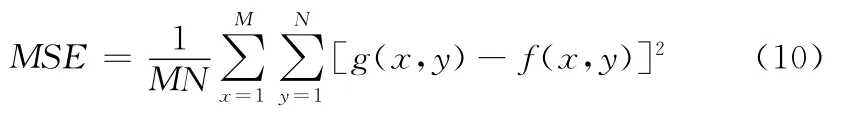
式中，f（x，y）、g（x，y）分别为原始图像的分量、滤波的分量图像在点（x，y）上的灰度值，M、N分别是x方向、y方向图像像素点的个数。

峰值信噪比PSNR反映滤波图像的失真程度，一般它的值越大就表示滤波图像的质量越好，其定义为

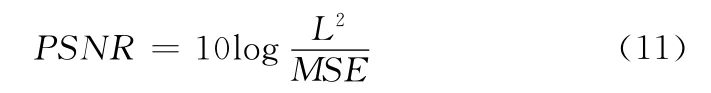
式中，L是滤波图像分量的灰度取值范围。

相关测度K值即表示滤波的分量图像和原始图像分量的相似程度，其定义为

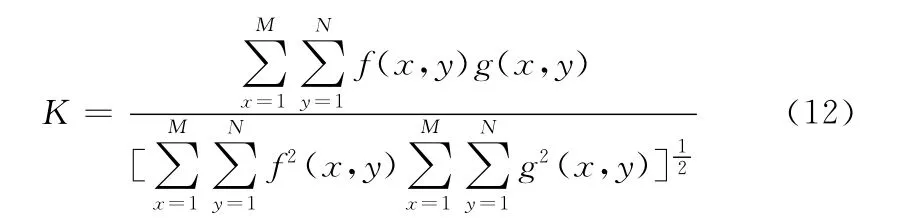
整幅图像的均方误差MSE、峰值信噪比PSNR值和相关测度K值取R、G、B三通道的均值。

3 仿真实验与结果

3.1 实验安排

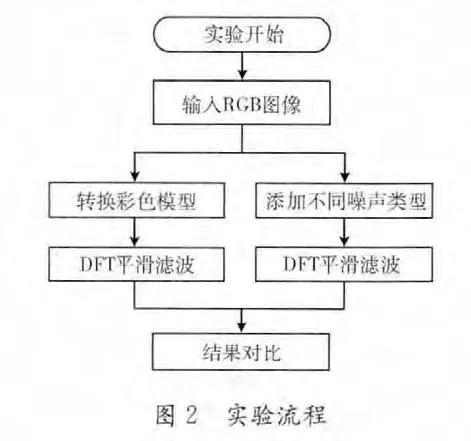
实验选用的彩色图像来源于参考文献［10］，其特征为8位无符号整形RGB彩色图像，TIFF格式，尺寸1197x1197，如图3（a）所示。实验分成两步:对输入的RGB图像加入不同的噪声类型，高斯噪声和椒盐噪声，比较采用DFT平滑滤波算法对两种常用噪声的滤波效果；将输入的RGB图像转化为不同的彩色空间，包括NTSC、HSV、HSI、YCbCr、CMY模型，采用DFT平滑滤波，比较对不同彩色空间图像的滤波效果。其流程如图2所示。

3.2 实验结果

对图3（a）加入均值为0，方差为0.01的高斯噪声，效果如图3（b）所示，并采用DFT平滑滤波，平滑结果如图3（c）所示；对该图加入噪声密度为0.05的椒盐噪声，效果如图3（d）所示，同样也采用DFT平滑滤波，平滑结果如图3（e）所示。

图3 DFT平滑滤波对加躁彩色图像的滤波效果

从图3可看出:DFT平滑滤波算法很好的消除了给RGB图像加入的高斯噪声和椒盐噪声，其结果均能较为清晰的看到图像的边缘和细节信息，获得了较好的平滑滤波效果，表1和表2的数据更加精确地表明了这一直观判断。

从表1和表2可看出:使用DFT平滑滤波算法对图3（a）平滑之后，图像及其分量的峰值信噪比PSNR值和相关测度K值均明显的增大，说明该算法对高斯噪声和椒盐噪声均具有良好的抑制作用；使用该算法对图3（a）平滑之后，图像的均方误差MSE值略高于加躁图像的MSE值，说明采用DFT平滑滤波算法对图像进行平滑，其过程付出了一定的细节模糊代价。

表1 对高斯噪声平滑结果的评价参数比较

表2 对椒盐噪声平滑结果的评价参数比较

将图3（a）转化成NTSC、HSV、HSI、YCbCr、CMY模型，分别采用DFT平滑滤波，平滑结果如图4所示。

图4 DFT平滑滤波算法对不同彩色空间模型的滤波效果

对比图3（a）和图4（a）－（f），可看出:DFT平滑滤波算法适用于对RGB、NTSC、HSV、HSI彩色图像的平滑，而对YCbCr、CMY图像的平滑效果很差；DFT平滑滤波算法对HSV、HSI、YCbCr和CMY彩色图像进行平滑滤波，会产生无意义的颜色，比如图4（c）和（d）中花杂的顶部出现了绿色边缘，而图4（e）和（f）表现的更为明显，这是由于对HSV、HSI、YCbCr和CMY图像的所有分量进行DFT频域滤波，改变了相关分量间的相对关系，从而使平滑图像产生了无意义的颜色。对HSV和HSI彩色图像使用DFT平滑滤波算法，局部虽会产生无意义的颜色，但根据人眼视觉特性，对彩色图像的细节分辩能力不强，远低于对亮度细节的分辩能力，即所谓的彩色细节失明［12］，DFT平滑滤波算法也可作为平滑HSV和HSI图像的一种方法。

图4（c）－（f）在排版中转为灰度图像，不能反映采用文中滤波算法对HSV、HSI、YCbCr和CMY图像进行平滑滤波之后的颜色变化，读者可自行运行程序进行验证。

4 结束语

通过实验可知，采用DFT平滑滤波算法对加入高斯噪声和椒盐噪声的彩色图像均具有良好的滤波效果，其适用于RGB、NTSC、HSV、HSI彩色空间模型图像的平滑滤波。

本文针对彩色图像的平滑滤波问题，提出了一种新的平滑滤波算法。传统的滤波算法基本上都是针对灰度图像的，而对彩色图像平滑滤波的方法通常限于采用线性空间滤波器或转换至其他的彩色空间模型进行平滑处理，本文利用DFT变换实现了基于频域滤波方法对彩色图像的平滑滤波，并且对该算法的去噪效果进行了分析，明确了其对彩色空间模型的适用范围，对丰富彩色图像平滑滤波的方法具有重要的促进作用。

［1］HAN Baoli，LIU Yangtao.Research and improvement of the image smoothing algorithm［J］.Computer Knowledge and Technology，2009，5（30）:8540－8542（in Chinese）.［韩宝立，刘杨涛.图像平滑算法的研究与改进［J］.电脑知识与技术，2009，5（30）:8540－8542.］

［2］YANG Huiyun，ZHANG Youhui，HUO Liling，et al.Application of Bayes decision and neighborhood averaging method on image denoising［J］.Computers Engineering and Application，2010，46（9）:149－151（in Chinese）.［杨会云，张有会，霍利岭，等.Bayes理论和邻域平均法在图像去噪中的应用［J］.计算机工程与应用，2010，46（9）:149－151.］

［3］LI Xuewei，ZHANG Xinrong.Automatic edge and detail preserving smoother for color image［J］.Computer Engineering and Applications，2010，46（3）:172－174（in Chinese）.［李雪威，张新荣.保持边缘和细节的彩色图像自动平滑［J］.计算机工程与应用，2010，46（3）:172－174.］

［4］Li P F，Wang S R，Jing J F.The segmentation in textile printing image based on mean shift［C］//Proceedings of the 10th Conference on Computer－Aided Industrial Design and Conceptual Design，2009:1528－1532.

［5］Wang Z Y，Boesch R，Waser L，et al.Mean shift segmentation applied to ADS40 data for automatic forest detection［C］//Proceedings of the International Conference on Information and Automation，2009:1099－1103.

［6］Jimenez－Alaniz J R，Pohl－Alfaro M，Medina－Banuelos V，et al.Segmenting brain MRI using adaptive mean shift［C］//Proceedings of the 28th IEEE Conference on Engineering in Medi－cine and Biology Society，2006:3114－3117.

［7］Mayer A，Greenspan H.An adaptive mean－shift framework for MRI brain segmentation［C］//IEEE Transactions on Medical Imaging，2009:1238－1250.

［8］WANG Yan，SUN Yi.Adaptive Mean Shift based image smoothing and segmentation［J］.Acta Automatica Sinica，2010，36（12）:1637－1644（in Chinese）.［王晏，孙怡.自适应Mean Shift算法的彩色图像平滑与分割算法［J］.自动化学报，2010，36（12）:1637－1644.］

［9］YANG Wenbin，XU Faqiang.Color imgage smoothing based on color space transformation［J］.Science ＆Technology Information，2009（35）:524－523（in Chinese）.［杨文兵，许法强.基于颜色空间转换的彩色图像平滑处理［J］.科技信息，2009（35）:524－523.］

［10］Rafael C Gonzalez.Digital image processing using MATLAB［M］.Beijing:Publishing House of Electronics Industry，2012.

［11］CHEN Yunlong，WANG Ping，WANG Peng.Degradation image restoration algorithm based on nonlinear iteration［J］.Computer Engineering，2010，36（4）:202－204（in Chinese）.［陈云龙，王平，王鹏.基于L－R非线性迭代的降质图像复原算法［J］.计算机工程，2010，36（4）:202－204.］

［12］LI Xuewei，ZHANG Xinrong.On edge－preserved Gaussian smoothing filtering algorithm［J］.Computer Applications and Software，2010，27（1）:83－84（in Chinese）.［李雪威，张新荣.保持边缘的高斯平滑滤波算法研究［J］.计算机应用与软件，2010，27（1）:83－84.］