基于DSP的混沌语音加密解密系统

葛秀梅， 仲伟波， 李忠梅， 范东升

(江苏科技大学 电子信息学院,江苏 镇江 212003)

0 引 言

随着Internet的普及及其传输速率的提升，网络传输语音已成为可能，但Internet的开放性对语音通信的安全提出了更高的挑战。语音信号具有数据量大、能量分布不均匀、冗余性高的特点[1]，而混沌系统根据少量参数就可以产生满足密码学基本特性的混沌序列，且混沌序列具有短期内可预测但长期不可预测的特点，非常适合作为加密密钥并已引起诸多学者的关注[2]。虽然近年研究发现基于混沌流同步加密的方法存在安全方面的问题[3]，但混沌加、解密技术已成为目前加解密的应用研究的热点[4-5]，并被成功用于语音和图像加解密中[6-12]。本文把混沌序列作为密钥，利用其他加密算法对语音进行加密以有效避免混沌流密钥带来的失密危险。

TI的5509A DSP由于其低功耗和快速计算能力常被用于语音信号处理中,本文基于该芯片设计并实现了一种混沌密钥语音加密系统，发送端先由根密钥产生混沌加密密钥，然后根据约定的IDEA(International Data Encryption Algorithm)加密算法对语音数据进行加密，加密后的语音密文经过传输到达接收端。发送端同时也将根密钥加密发送到接收端，接收端根据根密钥和混沌系统自动生成解密密钥。接收端根据计算出来的解密密钥对接收到的语音密文进行解密得语音明文。经测试，本文所给出的混沌语音加密系统具体较好的安全性和稳定性，可用于语音保密通信中。

1 混沌密钥及加密算法

系统中混沌语音加、解密可分为混沌密钥产生和IDEA加解密算法两部分。混沌密钥的产生是将Henon映射和改进后的Logistic映射级联生成初始混沌序列，然后对其进行非线性变换得到IDEA加密算法所需的128 b加密密钥。IDEA是James Massey和来学嘉提出的数据块加密算法，数据块长度为64 b，密钥长度为128 b[13]。IDEA算法相对来说是一个比较新的算法，其安全性研究也在不断进行，虽然已发现IDEA也存在诸多弱点，但目前已在PGP，SSL等工程中大量应用，仍不失为当前最优秀加解密算法之一[14]。

系统采用的Henon映射为：

(1)

其中：a=1.4；b=0.3。由于Henon序列取值在[-1.3,1.3]，在DSP的C代码中采用double类型保存所得的映射序列。系统根据用户输入初值x0,y0进行2 000次Henon映射迭代计算得到长度为2 000的迭代序列，将序列最后一个分别与第1 800个和第1 900个值相乘并取其小数部分，得到d1=(x1999*x1799)mod1，d2=(y1999*y1799)mod1，其中d1,d2∈(0,1)。

系统采用的改进的Logistic映射为:

xn+2=rxn+1(1-xn+1)+(4-r)xn(1-xn)

(2)

其中，xn∈0,1，当r∈[0,1.284 9)∪(3.477 6,4]时除个别点外系统都处于混沌状态，且迭代结果中不存在空白窗、稳定窗以及(0,1)范围分布不均匀等安全问题[15]。改进的Logistic映射的初值x0=d1,x1=d2，经过2 000次迭代后，将最后16个值保存在数组d[16]={x1984,x1985,…,x1999}中。

为得到IDEA加密算法所需的128 b二进制密钥，需将所得到的混沌序列d[16]作如下非线性变换：将区间[0,1]分成256个子区间，每个区间依次用0到255之间的整数表示，混沌序列d[16]中某元素落在第i个区间中，将其置换成整数i并标识该区间；若落入的区间i已标识过，则将i加1模256，直到得到新的整数为止。如此迭代，即可获得一个有16个不重复的序列{a0,a1,…,a15}，其中ai∈{0,1,…,255}，将其中元素用二进制数表示，即可得128 b二进制密钥。由于DSP的C语言规范中unsigned char数据类型长度为16 b，将上面得到的16个8 b密钥合并组成{b0,b1,…,b7}，其中b0=a0≪8+a1,…,b7=a14≪8+a15。

IDEA算法是一个分组长度为64位，密钥长度为128 b的分组加密算法，由于系统采用的5509A是16 b的定点处理器，为方便和效率考虑，将明文分成四个16 b的子分组：x1,x2,x3和x4并将其用unsigned short数据类型表示，这4个子分组作为第一轮的输入并进行运算，每一轮的输出作为下一轮的输入，经过8轮运算之后，得到最终的输出变换：y1,y2,y3,y4，将y2,y3两组交换，得到最终的四个密文子分组，最后将这四个子分组重新连接到一起产生密文。IDEA解密过程和加密过程一样，只是参与运算的密钥不同而已。IDEA具体每轮的计算过程如图1所示。

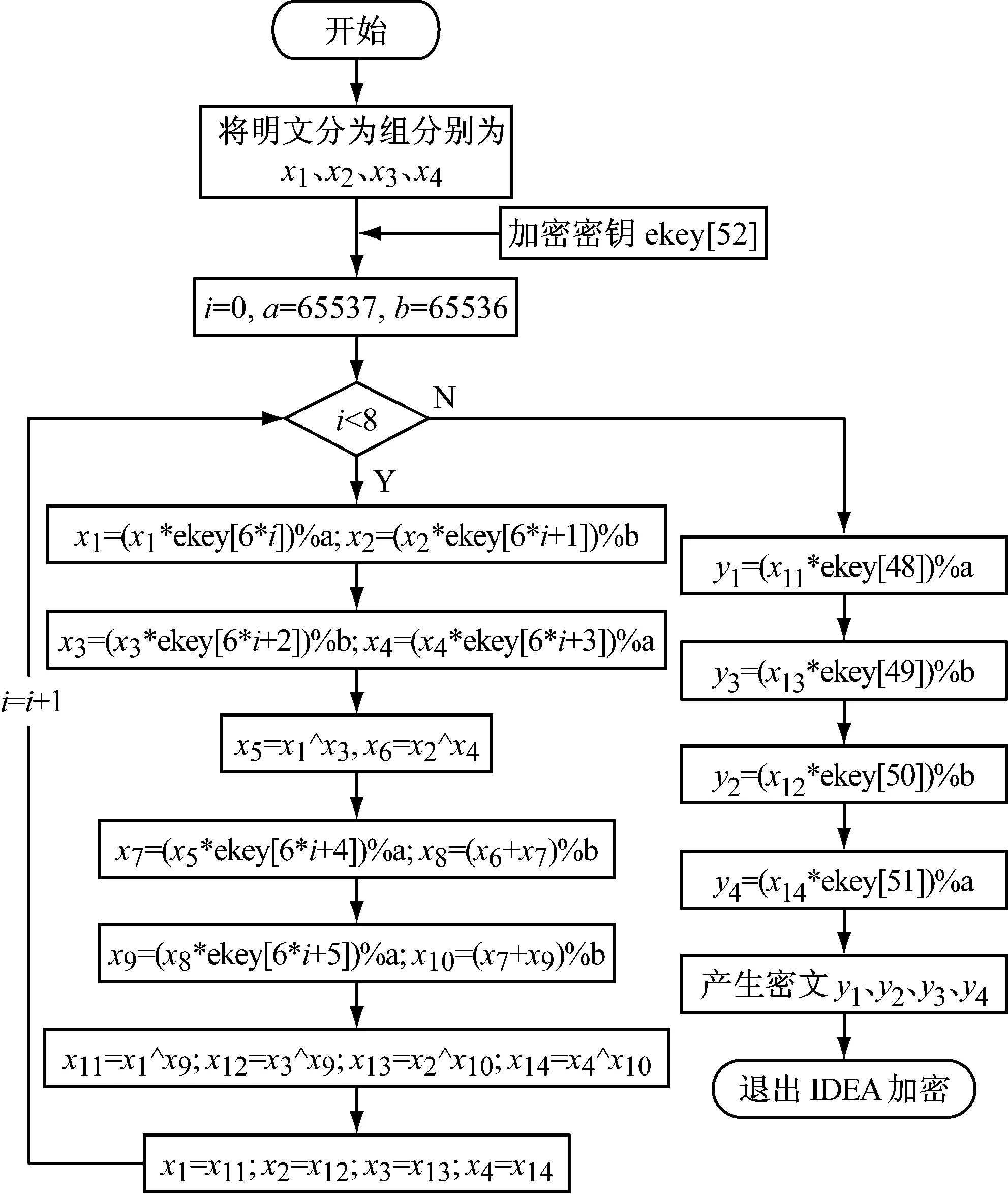
图1 IDEA加密流程图

由IDEA加密算法可知，在整个加密运算中总共需要52个16 b二进制子密钥，这52子密钥是根据128 b二进制混沌密钥生成的。52个加密密钥在DSP中实现过程如图2所示。由IDEA算法可知其加密过程和解密过程相同，所不同的是参与运算的密钥，52个解密密钥可由加密时所使用的52个加密子密钥计算得到，在DSP中实现过程如图3所示。其中inv()函数中要对65 537求余，因此该函数中所有变量的数据类型都为long，最后将inv()函数返回的数据强制转换为unsigned short类型，由于返回数据的取值在unsigned short类型表示的范围，强制类型转换不会产生错误。

2 语音加、解密的实现与测试

本文设计实现的混沌语音加、解密系统以DSP5509A为核心，使用CCStudio和XDS100V2仿真器进行开发调试。DSP5509A完成语音信号的加密解密算法并控制整个系统的运行，音频编解码芯片TLV320AIC23用来完成语音数据的采集和回放，模拟语音信号经过麦克风输入或线输入，通过TLV320AIC23使之转换为PCM码，PCM编码通过多通道缓冲串口McBsp进入DSP5509A，并存储在外扩SDRAM中。DSP5509A对语音PCM码数据进行混沌加密并将其通过以太网发送出去。接收端通过以太网得到语音数据密文和混沌根密钥，先根据混沌根密钥计算出IDEA解密密钥，然后把语音密文解密成明文。

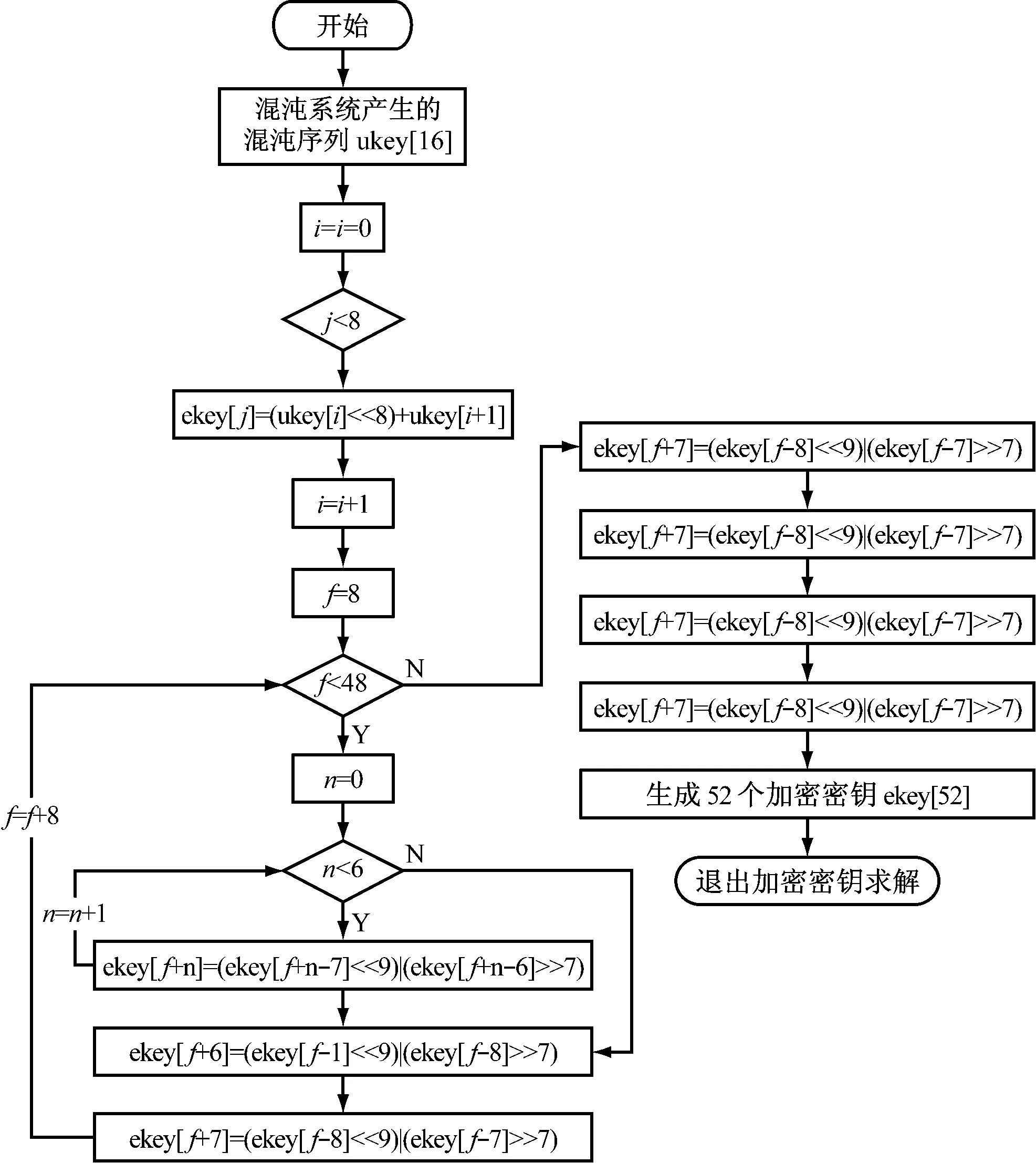
图2 加密密钥求解流程图

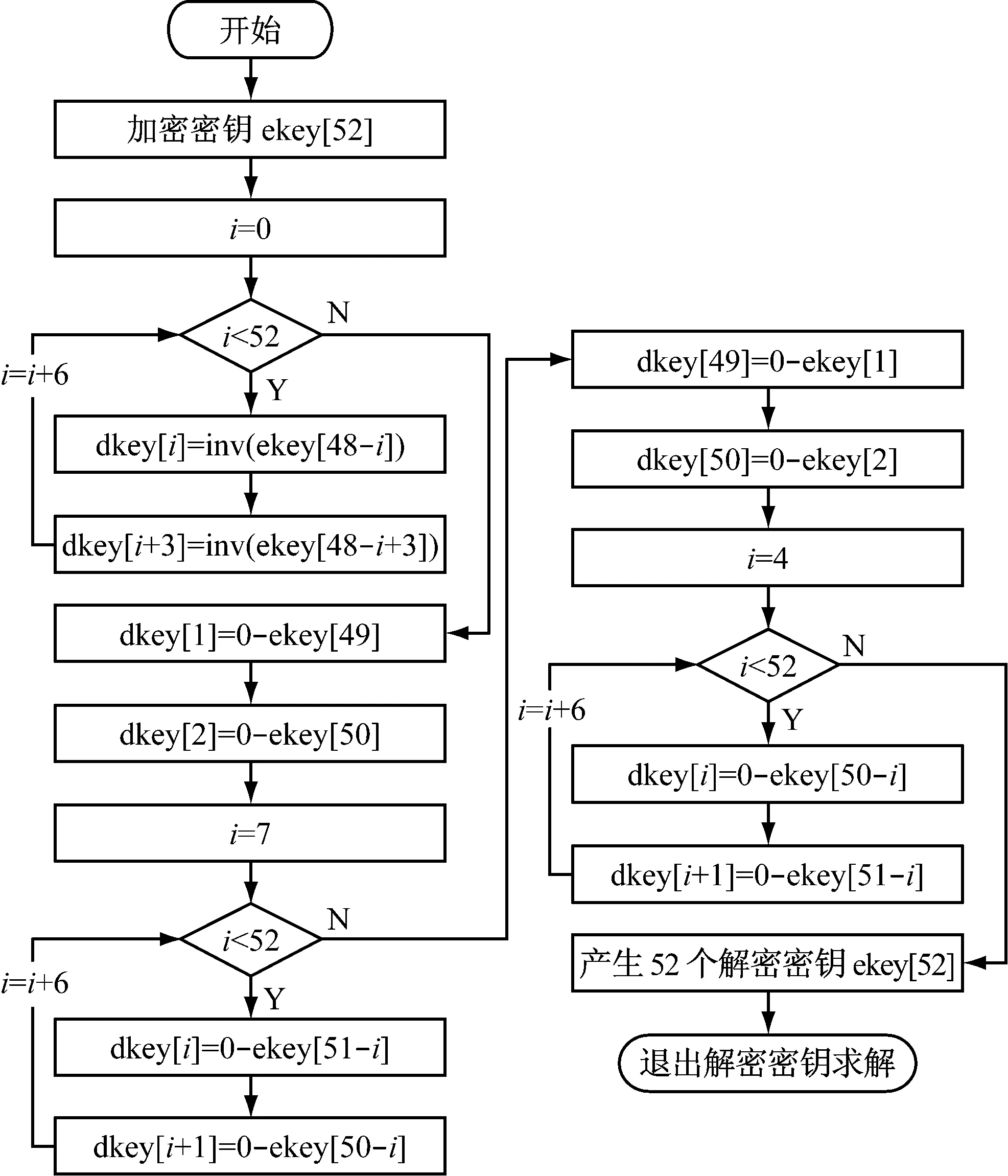
图3 解密密钥求解流程图

系统首先是初始化CSL库，设置系统DSP的工作频率为144 MHz，然后初始化IIC，主要包括设置地址模式为7 b地址模式、IIC传输速率为84 MHz、传输字节中包含16 b及打开数据环路模式，通过IIC对AIC23进行配置和管理，AIC23复位后设置AIC23的采样率为44.1 kHz。配置EMIF为全EMIF接口模式，并初始化DSP的外部SDRAM。对McBsp0的初始化后，打开McBsp0与AIC23进行数据交换。

为验证所设计的语音加、解密方案的可行性和代码的正确性与可靠性，先在CCS上进行算法的调试验证，采集从PC播放的音乐数据，随机保存200个连续数据，如图4(a)所示，对其进行混沌加密，加密结果如图4(b)所示，此次加密中使用的混沌根密钥，也即Henon映射的初值为0。将加密密文和根密钥通过以太网发送到接收板，接收板根据根密钥计算出解密密钥并对数据密文进行解密，解密后结果如图4(c)所示，解密结果与其明文完全一致。若在解密过程中使用的根密钥与加密根密钥不一致，解密结果则与原明文相差甚远，如图4(d)所示。

图4(a) 原始语音信号

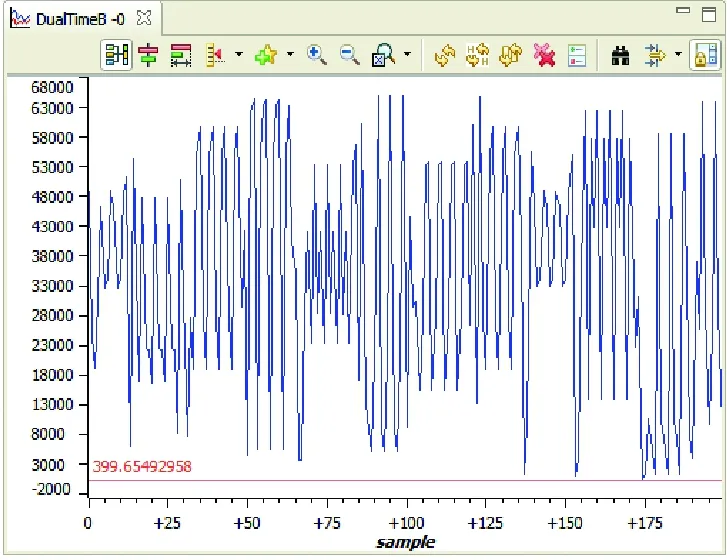
图4(b) 加密语音信号

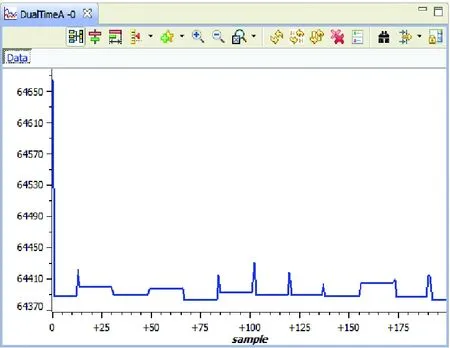
图4(c) 解密语音信号 图4(d) 错误解密语音信号

从以上结果可知，本文给出的基于混沌密钥的IDEA加解密方法适合网络语音加、解密，加密后的语音数据量不变，但数据本身变化很大，对语音网络传输不会造成带宽上的压力，同时也证明了本文给出的基于混沌密钥的语音加、解密算法对密钥的敏感性和有效性。

本文设计实现的语音混沌加、解密系统实物图如图5所示。图中左边的DSP板卡是加密端，右边的板卡是解密端，从PC机播放的wav格式的语音通过线输入传送到DSP板卡进行加密处理后，加密后的数据包经过以太网传送到另一端，另一端对语音包和根密钥包进行解密，由线输出连接到音响。

图5 混沌语音加解密系统实物图

3 结 语

本文中将混沌密钥和IDEA加密算法相结合进行语音加、解密处理以提供网络语音的安全性，混沌密钥的生成采用了Henon映射和改进的Logistic映射两种混沌映射级联迭代，将迭代结果经过非线性替换形成IDEA加密密钥，采用IDEA加密算法对语音信号进行了加解密。经多次加、解密测试表明，本文中设计实现的混沌加密系统能够满足语音传输的实时性要求，使得该系统具有一定的民用价值和军用价值，尤其在物联网、海上捕鱼渔船之间的通信、多媒体通信等方面有着广泛的应用。但在语音传输的过程中，语音会出现丢包现象，说明该系统还有待进一步优化，才能达到更好的加密效果。

[1] 陆 洋，张 超，陆建华,等. IEEE802.11无线局域网接入环境下语音传输容量[J]. 清华大学学报(自然科学版), 2008, 48(1): 39-42.

LU Yang, ZHANG Chao, LU Jian-hua,etal. Voice transmission capacity under the IEEE802.11 wireless LAN access environments[J]. Journal of Tsinghua University (Natural Science), 2008, 48(1): 39-42.

[2] 杨义先，钮心忻. 应用密码学[M]. 北京:北京邮电大学出版社, 2005: 295-360.

[3] 尹汝明，袁 坚，山秀明,等. 混沌密码系统弱密钥随机性分析[J]. 中国科学：信息科学, 2011, 41(7): 777-788.

YIN Ru-ming, YUAN Jian, SHAN Xiu-ming,etal. Weak key randomness analysis of chaotic cryptosystems[J]. Science China: Information Sciences, 2011, 41(7): 777-788.

[4] 陈铁明，蒋融融. 混沌映射和神经网络互扰的新型复合流密码[J]. 物理学报，2013, 62(4): 1-7.

CHEN Tie-ming, JIANG Rong-rong. A new composite stream cipher of chaotic mapping and neural network mutual interference[J]. Acta Physica Sinica, 2013, 62(4): 1-7.

[5] 樊 雷,茅耀斌,孙金生,等.一种结合猫映射与Logistic映射的语音加密算法[J].控制与决策, 2004, 19(10): 1167-1170.

FAN Lei, MAO Yao-bing, SUN Jin-sheng,etal. A voice encryption algorithm combination of cat map and Logistic map[J]. Control and Decision, 2004, 19(10): 1167-1170.

[6] WANG Xing-yuan, TENG Lin. An image blocks encryption algorithm based on spatiotemporal chaos[J].Nonlinear Dynamics, 2012, 67(1): 365-371.

[7] E.Mosa, N.W.Messiha, O.Zahran. Encryption of speech signal with multiple secret keys in time and transform domains[J]. International Journal of Speech Technology, 2010, 13(4): 231-242.

[8] Long Jye Sheu. A speech encryption using fractional chaotic systems[J]. Nonlinear Dynamics, 2011, 65(1/2): 103-108.

[9] E.Mosa, Nagy W. Messiha, Osama Zahran. Chaotic encryption of speech signals[J]. International Journal of Speech Technology, 2011, 14(4): 285-296.

[10] 田丽平. 基于混沌映射的真彩数字图像安全通信[J].实验室研究与探索, 2006, 25(9): 1093-1095.

TIAN Li-ping. True color digital images for secure communication based on chaotic map[J]. Research and Exploration in Laboratory, 2006, 25(9): 1093-1095.

[11] Mirzaei, Yaghoobi, Irani. A new image encryption method: Parallel sub-image encryption with hyper chaos[J]. Nonlinear Dynamics, 2012, 67(1): 557-566.

[12] 汪永爱，王文海. 基于DSP嵌入式混沌密码话音通信系统的设计[J]. 实验室研究与探索,2007,26(12):64-66.

WANG Yong-ai, WANG Ji-hai. The design of voice communication system based on DSP embedded chaos password[J]. Research and Exploration in Laboratory, 2007, 26(12): 64-66.

[13] LAI Xue-jia, James L. Massey. A Proposal for a New Block Encryption Standard[J]. Proceedings of Advances in Cryptology, 1991, 389-404.

[14] Alex Biryukov, Jorge Nakahara Jr, Bart Preneel,etal. New Weak-Key Classes of IDEA. F. Bao, R. H. Deng, S. Qing. Lecture Notes in Computer Science[C]. Springer-Verlag, 2002: 315-326.

[15] 万佑红，李俊刚. 一种基于Logistic的改进混沌映射及其性能分析[J]. 信息与控制, 2012, 41(6): 675-680.

WAN You-hong, LI Jun-gang. The improvement and performance analysis of chaotic based on Logistic map[J]. Information and Control, 2012, 41(6): 675-680.