小半径、大深度隧道贯通测量的研究与实践
程远达,傅晓明
(上海市测绘院,上海 200063)
1 引言
在城市范围内,为节约土地资源一般采用地下隧道来满足轨道交通、公路工程和大型输水管道的需要,为减少对城市运营的影响,隧道绝大多数采用盾构法施工。隧道贯通测量的目的就是确保盾构按照设计的线路中心向前延伸,并准确进洞。一般的对采用盾构法施工隧道的设计,贯通区间长度≤1.5 km,工作井深度≤20 m,中心平面曲线半径不小于 500 m,这样条件的隧道工程在贯通测量作业时按规范中相关技术要求施测,取得较好贯通精度已有许多成功的案例。而当隧道设计长度加长至 2.5 km~2.8 km,工作井深度加深到 40 m,贯通区间中心线有多个半径小于500 m的曲线段,而且贯通测量中误差(≤±50 mm)的要求不变,按照规范规定的技术要求是难以满足工程贯通的需要,必须对贯通测量误差进行估算,并对贯通测量中的关键环节进行设计和控制。本文主要讨论小半径、大深度隧道贯通测量的精度研究,并在关键环节设计了针对措施和在实际工程进行应用实践。
2 隧道贯通测量的误差来源
隧道工程施工一般是盾构由一侧竖井开始,掘进至另一侧竖井结束,在盾构推进线路的纵向、横向及竖向会出现贯通误差,其中纵向贯通误差主要影响隧道中线的长度,而横向误差和高程贯通误差对工程的贯通影响最大,已有隧道工程贯通测量的经验证明高程贯通误差容易控制,因此控制好横向误差是贯通测量的关键。
从隧道贯通测量的整体工艺看,主要包含了地面控制测量、联系测量、地下平面控制测量、地下高程测量、盾构姿态测量和洞门测量等,因此贯通测量的误差主要来源如下几方面:①地面控制测量所引起的横向贯通中误差m1;②盾构出洞处竖井联系测量中误差m2;③地下导线测量所引起的横向贯通中误差m3;④盾构姿态的定位测量中误差m4;⑤盾构进洞处洞口中心坐标测量中误差m5。
《城市轨道交通工程测量规范》(GB50308-2008)规定,地面控制测量的中误差为±25 mm,联系测量的中误差为 ±20 mm,地下导线的测量中误差为 ±30 mm[5]。在贯通测量误差来源中,地面控制测量、盾构姿态和盾构进洞处洞口中心坐标测量的误差不受地下施工条件的影响,只有联系测量、地下导线测量随隧道的设计条件差异而采取不同的技术措施。工作井深度大,造成联系测量成果不稳定,而且联系测量的横向中误差≤±20 mm,其值又与隧道的长度相关,长度越长必然要求联系测量的起始边方位角精度高;当隧道区间长度长且中心线多个半径小于 500 m曲线段时,地下导线点的平均边长缩短、设站数随之增加,地下导线的累积误差明显增大。因此针对小半径、大深度隧道贯通测量必须控制好联系测量、地下导线测量这两个关键环节,通过研究贯通的误差,制订科学合理的技术方案以满足联系测量的中误差为±20 mm和地下导线的测量中误差为 ±30 mm的要求,实现盾构准确进洞。
3 关键测量环节的技术设计
在小半径、大深度隧道工程条件下,研究分析联系测量和地下导线测量工序的误差来源,正确估算测量误差,是制订科学合理的技术方案和措施的基础。
3.1 联系测量传递至井下起始边方向中误差的确定
联系测量的主要目的是把地面控制点的坐标准确

式中,mt为井下起始边的方向中误差,L为地下导线的长度,m2联系测量的中误差为 ±20 mm。
3.2 联系三角形测量的误差分析与观测指标设计
联系三角形法测量要满足井下起始边的方向中误差mt≤±1.65″的要求,对其测角测距的技术要求分析如下。联系三角形定向测量(如图1所示)是将工作井上的地面控制点(近井点A)和已知方向,通过3根竖直的钢丝组成左右三角形,通过测量井上井下的γ、γ'角和测站至钢丝的距离(a、b边)、钢丝间的距离(c边),按余弦定理校核三角形内符合,在满足限差要求后,计算α角和钢丝的方位角和坐标,将坐标准确地传递至井下地下导线起始点(A'),方位准确地传递至起始边。α按式(2)计算。传递至地下,作为地下导线的基准。目前应用较多的方法有陀螺定向法、钻孔投点法、联系三角形法和导线定向法。而要在工作井深度深的条件下取得高精度的坐标传递和方位传递,经常采用联系三角形法实施。联系测量的中误差≤±20 mm,一般可理解为联系测量坐标、方位传递对地下导线最远端点引起的横向误差,施工隧道长度的长度越长要求井下起始边方向中误差应越小。假使隧道长度为 2 500 m时,井下起始边方向中误差(mt)依据(1)式计算可得≤±1.65″。

图1 联系三角形定向示意图

为了确定角度γ与边长a、c边的测量误差对于角度α的影响,微分式(2)后可得:

式中ms为测距中误差,mβ1为井上或井下测边对α角引起的误差,ρ取206265。角度γ测量对α引起的误差为:

式中ma为角度γ的测角中误差。
根据误差传播定理,推出地下导线起始边方向中误差mt为:

依据式(3)、式(4)、式(5)地下导线起始边方向中误差为:

当联系三角形定向中距离测量选用Ⅰ级测距精度(1 mm±1 ppm×D)的仪器和反射片以取代钢尺量距时,其测距中误差ms为 1 mm,而γ角一般控制在1°以内,当ρ取206265,依据式(6)可计算a、c边长与角度测量中误差对起始边影响,结果如表1所示:

边长a、c和角度γ测量误差对起始边方向中误差的影响 表1
由此表1可见,联系三角形测量传递至井下起始边的方向中误差 mt≤±1.65″,必须将的值控制在0.5以内,且角度 γ的测角中误差应≤±0.71″,依据《精密工程测量规范》(GB/T15314-94)规定,测角采用0.5″级全站仪按9测回测量。
3.3 地下导线测量的误差分析与观测指标设计
地下导线测量中起始边对贯通误差的影响已在联系测量中考虑,在不考虑起始边方位影响的前提下,依据式[1](7)可知地下导线测量对隧道贯通横向误差主要来源于角度测量误差,边长测量误差对地下导线横向误差的影响较小。

式中:mβ为测角中误差,n为导线测站数,ρ取206265。
当地下导线的长度为2.5 km时,若地下导线的测量中误差 m3≤±30 mm,依据式(7)可计算导线测站数、导线边长和测角中误差的关系,如表2所示。

导线测站数、导线边长和测角中误差关系 表2
从表2中可以看出,当地下导线的设站数超过16时,测角中误差应≤±1″,根据《精密工程测量规范》(GB/T15314-94)的规定,介于二级(0.71″)与三级(1.41″)测角中误差之间,为确保地下导线的误差 ≤±30 mm,测角采用0.5″全站仪施测其测回数为9,测距采用I级测距精度(1 mm±1 ppm×D),往返各观测2测回。
4 工程实例中控制措施的应用
青草沙水源地原水工程是上海“十一五”重大民生工程,其中岛域输水隧道工程(如图2所示)由输水泵站接出2根φ5500原水管,设置了水库出水输水闸井(以下简称3号井)、输水管线中间盾构工作井(以下简称2号井)和长江过江管岛域工作井(以下简称1号井)等3个工作井,盾构推进施工分为东线和西线,由1号井出洞、2号井进洞(长度 2.5 km),2号井出洞、3号井进洞(2.8 km)。1号井井深约 40 m,2号井井深约 24 m,3号井井深约 18 m,此工程是一个典型的小半径、大深度隧道工程。

图2 岛屿段输水隧道工程示意图
4.1 联系测量控制措施
按照本文3.2确定的联系测量观测技术指标,采用TCA2003全站仪,测距使用Leica公司的标准反射片,测角分3组,共9测回。4条隧道联系三角形测量的成果统计如表3所示:
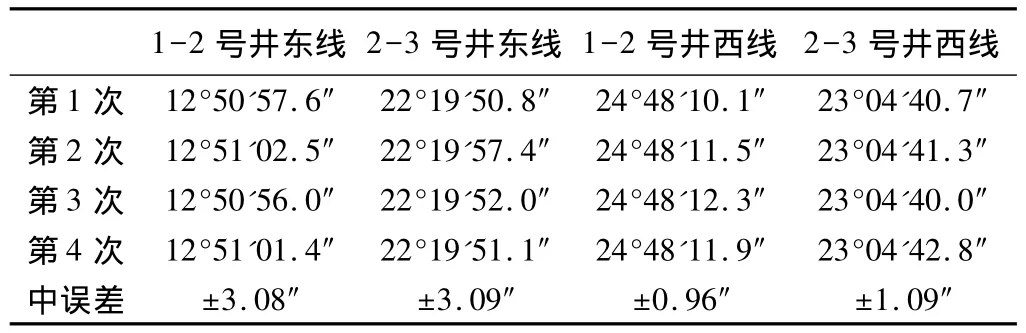
联系三角形起始边中误差计算表 表3
由表3可以看出,1-2号井东线、2-3号井东线联系三角形传递井下起始边的方向中误差超过了±1.65″,最终1-2号井东线贯通的误差为 8.7 cm,接近了规范规定的限差。为此根据本工程联系三角形测量的要求和现场条件分析误差来源,提出改进措施。自2-3号井东线第3次测量开始,把措施落实到实际测量环节中,自此起始边的方向中误差≤±1.65″,贯通误差(如表4所示)也满足 ±5 cm的要求,由此可见联系三角形测量过程中确定的联系测量观测指标是科学合理的,但保证观测指标与估算结果的一致,除规范规定的要求外加强的措施如下:
(1)工作井深度大,确保钢丝的垂直性与稳定性,选定φ0.5 mm钢丝,悬挂重锤的重量为 13 kg;
(2)在工作井大小确定的情况下,缩短近井点到O1钢丝的距离(约 9 m),减小a/c的值;
(3)改善观测的环境,如井上吊钢丝的架子高度增加 0.5 m,去除施工围栏对观测视线的干扰,同时用白纸作为钢丝观测的背景以提高角度观测的分辨力;
(4)保持观测过程中钢丝的稳定,如重锤在阻尼液中至少有1/5高出阻尼液面,井下工作面禁止施工人员来回走动,减少对钢丝干扰;
(5)选择合适的天气和观测时间,避免温度变化较大的时间段,避免太阳光线对钢丝的漫射;
(6)钢丝悬挂完毕后稳定 30 min,并比对井上、井下钢丝间距离,其较差小于 1 mm后,方可开始角度观测。

贯通误差统计表 表4
4.2 地下导线测量控制措施
地下导线测量的关键环节在于角度测量,采用TCA2003全站仪按左4右5共9测回进行自动观测,由于隧道深度深且线路中心的半径小,造成地下隧道测量环境不稳定,即使按照规定的技术要求观测,但很有可能造成实际的测角中误差大于0.71″或角度之间存在小值粗差,为此在工程中采取了一下的控制措施:
(1)地下导线的控制点全部设置为强制归心标,消除对点误差;
(2)隧道内弯道处每 200 m增加鼓风机,改善地下导线观测的环境,提高测角的稳定性;
(3)加强前后各次地下导线角度观测数据的对比分析,对角度异常的测站进行重复测量。以其中一条隧道最后一次地下导线(如图3所示)测量数据为例进行分析,如表5所示:
地下导线比对中与上次角度之差可以基本判断控制点的变动或角度异常,与上次角度之差的累积可以确定控制点的变动或角度异常的测站,从表5中可以看出,LK8点发生了变动,而测站LK6、LK11存在角度误差进行返工重测,经重测后角度的累积差为-0.8″,最后本条隧道平面贯通误差 8 mm。

图3 地下导线布设示意图

地下导线角度测量值分析 表5
5 结语
小半径、大深度隧道的贯通测量给测绘工作带来了新挑战,通过抓住联系测量和地下导线测量这两个关键,进行严密的精度估算并制定科学合理的观测技术指标,对测量的数据及时分析寻找异常,并结合现场条件制定可行的保障措施,不但可以克服小半径、大深度条件隧道给贯通测量精度带来的不利影响,而且可以获取高精度的测绘成果,为工程施工提供优质的测绘保障。
[1]张正禄.工程测量学[M].武汉:武汉大学出版社,2005.
[2]高绍伟.激光铅垂仪向上投点在地铁隧道工程中进行联系测量的实践[J].北京测绘,2008(2):57~60.
[3]王启善.特长距离高精度巷道贯通测量方案设计及精度分析[J].煤矿安全,2011,42(3):135~138.
[4]姚文强.国内长距离跨江隧道一次性掘进贯通测量关键技术研究[J].城市勘测,2012(3):118~121.
[5]GB50308-2008.城市轨道交通工程测量规范[S].
[6]GB/T15314-94.精密工程测量规范[S].

