Curvature Theory for Point-Path and Plane-Envelope in Spherical Kinematics by New Adjoint Approach

WANG Wei and WANG Delun*

Department of Mechanical Engineering,Dalian University of Technology,Dalian 116024,China

1 Introduction1

HUNT[1]indicated that the fixed and moving centrodes together form a logical starting-point,on which a theory of instantaneous planar kinematics of a lamina is built.But apart from limited success,nobody had yet succeeded in fully developing a unified axode-based theory of spatial kinematics.Although several papers[2–4]related to the spherical and spatial kinematics have been published and the axodes are referred to by some research work[5–11],the axodes did not play a due role.For a rigid body in spatial motion,the moving and fixed axodes are both ruled surfaces and contact tangentially along the instantaneous screw axis(ISA).A point,a straight line or a plane of the moving body is viewed as adjoint to the moving and fixed axodes,respectively,in the moving and fixed Cartesian frames.The planar Cesaro’s adjoint approach[12]is naturally extended to a spatial problem to reveal the kinematic invariants of the axodes and build the relationship of the axodes and the trajectory traced by the point,line or plane.Spherical motion cannot only be taken as the extension of plane motion but also be viewed as the special form of spatial motion.With regard to the spherical motion,the axodes are conical surfaces with their vertexes coincident at the rotation center.The geometrical properties of the axodes are totally reflected by spherical image curves of the straight generatrices.The spherical image curves of the axodes are spherical centrodes for spherical motion of the rigid body.Thus research on spherical kinematics can set up a bridge from the centrode-based planar kinematics to the axode-based spatial kinematics.

The spherical kinematics was previously studied by DOBROVOLSKII[13],CAPELLEN,et al[14],MULLER[15].VELDKAMP[16]extended the right-angle theorem from plane kinematics to spherical kinematics,and obtained the spherical Euler-Savary equation and Bobillier theorem.The instantaneous angular velocity vector and its derivative were applied to the spherical slider-crank mechanism by KAMPHUIS[17].YANG,et al[18],defined the characteristic numbers to describe the spherical curve to a given order.Then the points of the rigid body in spherical motion,whose loci have the same characteristic number,can be located.SODHI,et al[19],derived the algebraic equations of the axodes for the spherical 4R mechanism and determined the order is 16.DOWLER,et al[20–21],extended the multiply separated position concept to spherical kinematics and designed the four-bar spherical mechanism through Burmester theory.MCCARTHY[22]used the Euler parameters to define a kinematic mapping of the spherical displacement to a point on a hypersphere of unit radius.The instantaneous properties of spherical motion were reflected by the differential geometry of curves on a hypersphere.TING,et al[23–24],pioneered the study of the instantaneous kinematics of a plane in spherical motion through the canonical systems.CHIANG,et al[25–27],systematically studied the kinematics of spherical mechanism.Although the complicated and lengthy algebraic equations of the axodes for the spherical motion were derived[19],the kinematic invariants and the geometric significance haven’t been thoroughly demonstrated.Actually,the axodes can occupy an important fundamental place not only in the kinematics but also in the mesh principle of the gear transmission.For instance,the mesh principle of the parallel cylindrical gears was established on the centrode-based Euler-Savary equation.WANG,et al[28],extended the planar adjoint approach to spatial problems.On this basis,a new spherical adjoint approach is introduced to set up the systematical groundwork for the axode-based curvature theories of spherical motion.

This paper is structured as follows.Section 2 shows how to describe the spherical motion by the adjoint approach.The vector equations of the instant center are derived in a concise form.The kinematic meanings of the invariant-induced geodesic curvature are presented to reveal the intrinsic properties of the spherical centrodes in section 3.In section 4,the spherical centrodes are taken as original curves to study the point-path based on the Darboux frame and fixed point conditions.For the plane-envelope,the Frenet frame and the construction parameters can be utilized to locate the planes whose envelope surfaces have the higher order osculating properties with specific surfaces.The spherical four-bar linkage is taken as an example in section 6 to demonstrate the effectiveness of the spherical adjoint approach.

2 Spherical Adjoint Approach

The spherical relative motion of a rigid body to a fixed body can be described by the moving Cartesian coordinates{RO;im,jm,km}attached to the moving body to the fixed coordinates{RO;if,jf,kf}.If a reference line of the moving body through the sphere center O is chosen,the spherical motion of the rigid body can be viewed as the motion along with the line and the rotation about the line.In particular,the reference line is collinear with the coordinate vector kmof{RO;im,jm,km}.As shown in Fig.1,the direction angles of kmin{RO;if,jf,kf}are(θ1,θ2).The angular displacement θ3of the moving body relative to the fixed body about kmcan be defined by the inclined angle of coordinate vectors imand iton the coordinate plane RO-itjtof the Cartesian coordinate system{RO;it,jt,km},of which the coordinate vector itis determined by it=km×kf.The relative position relation of the moving and fixed coordinate systems is

where s and c are the abbreviations of sine and cosine.

With the spherical motion of the rigid body,the reference line traces a conical surface Skin{RO;if,jf,kf},which intersects with the spherical surface with radius R at spherical curve Γk.The vector equation of Γkin{RO;if,jf,kf}is

where s is the arc length of Γkand n(s)is the unit normal vector of the spherical surface at point Ok.

For a point P on the spherical surface of the moving body,it can be viewed as adjoint to the reference line.In the spherical adjoint approach,the conical surface Skis taken as original ruled surface and spherical curve ΓPtraced by P is spherical adjoint curve to Sk.Since Skis a conical surface,its geometrical characteristics can be totally reflected by Γk.As shown in Fig.2,we can set up the Darboux frame{Rk;α,n,v}on Γk,whose three coordinate vectors are

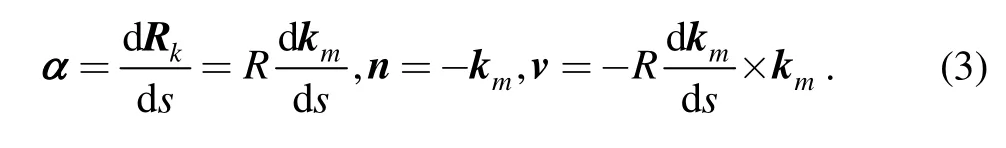
The differential formulas of{Rk;α,n,v}are

where invariant kgkis the geodesic curvature of Γk.

Fig.2.Spherical point-path adjoint to the original ruled surface

Based on the spherical adjoint approach,the vector equation of ΓPcan be described by{Rk;α,n,v}as

where(x1,x2,x3)are the relative coordinates of P in{Rk;α,n,v}.The position relation of{Rk;α,n,v}and{RO;im,jm,km}is

where θ is the angle between vectors α and im,and is function of the arc length s.The position vector of P in{RO;im,jm,km}is written in terms of the Cartesian coordinates(xPm,yPm,zPm)or the spherical coordinates(R,ξPm,ηPm)as

Taking the derivative of Eq.(5)with respect to the arc length s and substituting the so-obtained equation into Eq.(6),we have

where the variable with an overdot represents the derivative with respect to s,and similarly hereinafter.In particular,if P is a fixed point on the spherical surface in{RO;if,jf,kf},the relative coordinates(x1,x2,x3)must satisfy the spherical fixed point conditions A1=A2=A3=0.Using the chain rule of differentiation,we have dRP/ds=VP·dt/ds=0.It means P is a spherical instant center of the moving body and is defined as P0.Through Eqs.(8)and(9),the relative coordinates(x1,x2,x3)of P0in{Rk;α,n,v}at any instant can be determined by

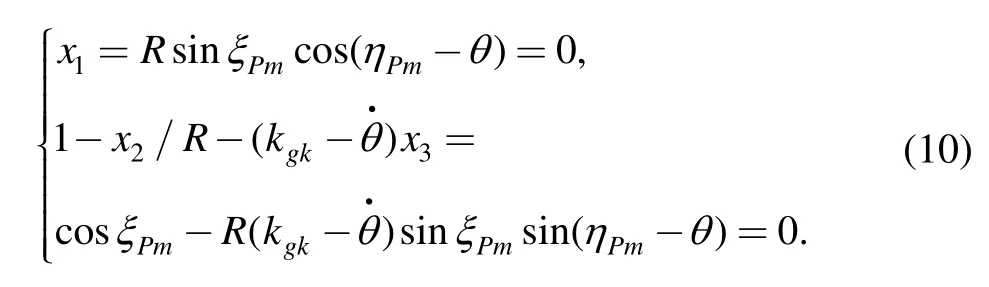
Then the condition equations of the spherical coordinates(ξP0,ηP0)of P0in{RO;im,jm,km}are

Through the above equation and the Darboux frame{Rk;α,n,v},we can see the instant center P0locates on the great circle on the normal plane of Γkat the point Ok.

3 Moving and Fixed Spherical Centrodes

MOZZI[30]firstly introduced the concept of ISA,and CHASLES[31]definitely pointed out the spatial motion of a rigid body is the composite of the rotation about the ISA and the translation along the ISA,or the screw motion.For spherical motion,the ISA is determined by the vector RP0and passes through the rotation center.As the motion of the rigid body,the ISA generates ruled surfaces Sfin{RO;if,jf,kf}and Smin{RO;im,jm,km},which are called the fixed axode and the moving axode respectively.The geometrical features of the two axodes can reflect motion features of the rigid body,or the axodes are geometric representation of the motion.

In the spherical adjoint approach,the axodes can be taken as original ruled surfaces to describe the kinematic properties of the rigid body.For spherical motion,both the axodes are conical surfaces with their vertexes at the rotation center and the geometrical properties of the axodes are totally reflected by the geodesic curvature of the spherical image curves of the straight generatrices.The fixed and moving axodes can be mapped onto unit sphere to obtain two spherical curves,which correspond to the fixed and moving centrode traced by the spherical velocity center respectively in the fixed and moving system,as shown in Fig.3.

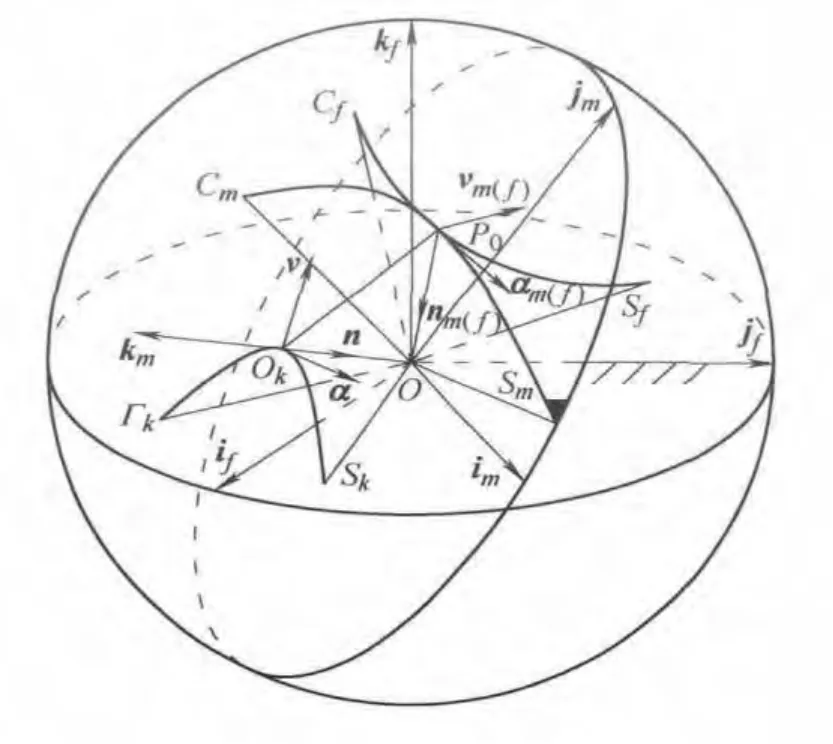
Fig.3 Spherical centrodes mapped by the two axodes

3.1 Spherical moving centrode and

its geodesic curvature

The relative coordinates(x1,x2,x3)of P0in{Rk;α,n,v}can be transformed into{RO;im,jm,km}and equation of the spherical moving centrode Cmcan be obtained.Through Eqs.(5),(8)and(11),the vector equation of Cmis

In{RO;im,jm,km},vector n is a fixed vector and vectors α=eI(θ),v=eII(θ)are vector functions of a unit circle on coordinate plane RO-imjm.Based on the properties of vector function of a unit circle,the derivatives of α and v with respect to θ are dα/dθ=v and dv/dθ=-α.Then the differential relationship between s and arc length σmof Cmis

Darboux frame{Rm;αm,nm,vm}of Cmis established as

The geodesic curvature kgmof Cmcan be calculated as

3.2 Spherical fixed centrode and its geodesic curvature

The instant velocity center of the rigid body in spherical motion forms spherical fixed centrode Cfin{RO;if,jf,kf}for all instants.According to Eq.(12),the vector equation of Cfis

Through Eq.(4),the differential relationship between s and arc length σfof Cfis

Comparing Eqs.(13)and(17),we find that the differential arc length of Cfis equal to that of Cm,or dσf=dσm=dσ.Thus Cmrolls on Cfon the unit sphere without sliding.Darboux frame{Rf;αf,nf,vf}of Cfis set up as

Comparing above equation with Eq.(14),we can see that{Rf;αf,nf,vf}of Cfcoincides with{Rm;αm,nm,vm}of Cmat the instant center.By taking derivative of the first expression of above equation with respect to σf,we have geodesic curvature of Cf,which is

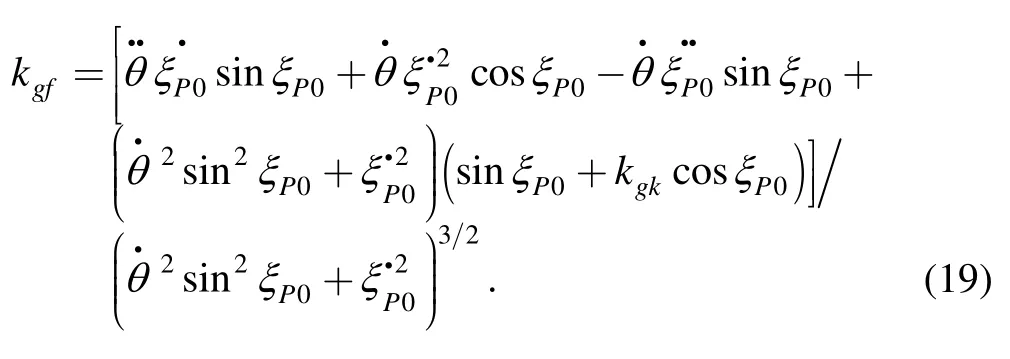
The induced geodesic curvature kg*of the spherical fixed and moving centrodes can be deduced by subtracting Eq.(15)from Eq.(19),that is

The relative coordinates of point Okin{Rk;α,n,v}are all zero,so the velocity vector of Okis obtained as

Since the spherical motion of rigid body can be viewed as the rotation around the ISA instantaneously,the velocity vector of Okcan be deduced in another way,that is

where ω is the angular velocity vector of the moving body around the ISA.Through Eqs.(21)and(22),the angular velocity ω is

The above equation demonstrates the kinematic meanings of the kinematic invariant-induced geodesic curvature kg*of the axodes(spherical centrodes).From Eqs.(13)and(17),Eqs.(14)and(18),we obtain the following conclusions:

For the relative spherical motion of the moving body to the fixed body,there exist a spherical moving centrode in the moving body and a spherical fixed centrode in the fixed body respectively.The two centrodes’Darboux frames are coincident with each other and the differential arc lengths of the two centrodes are equal.The spherical moving centrode rolls on the fixed centrode without sliding.

The above conclusions can be expressed as

4 Curvature Theory for a Point in Spherical Motion

4.1 Geodesic curvature of a spherical point-path

The moving and fixed axodes(spherical centrodes)together imply intrinsic properties of the spherical motion of a rigid body.Based on the axodes,the curvature theories for spherical motion can be established in an intuitive and concise way.Without loss of generality,we focus on point-path on the unit sphere.

For a point P of rigid body in spherical motion,it traces a spherical curve ΓPin{RO;if,jf,kf},which can be designated as an spherical adjoint curve to the fixed axode Sfor the spherical fixed centrode Cf,as shown in Fig.4.

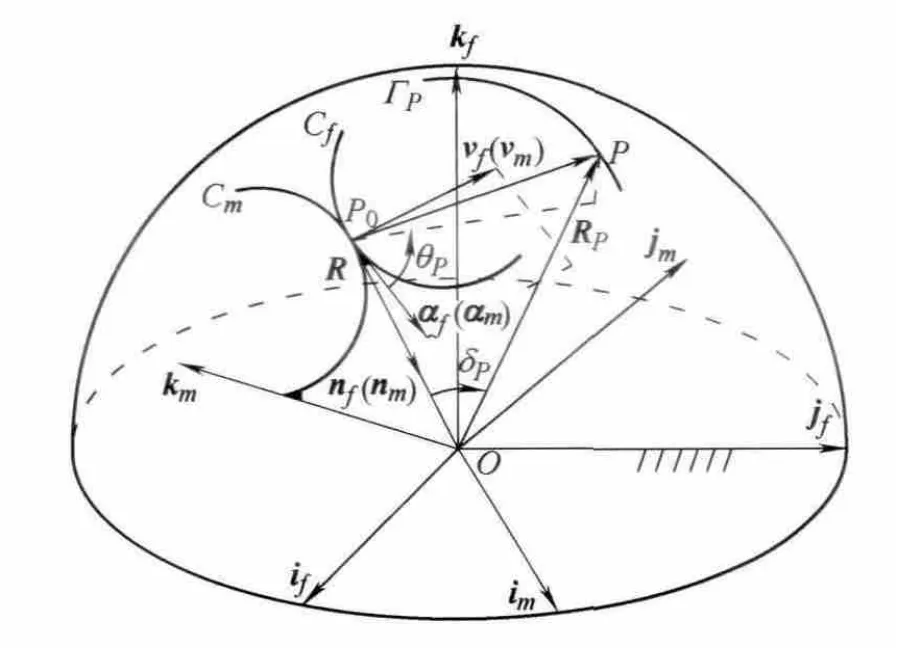
Fig.4 Spherical point-path adjoint to the spherical centrodes

Through the spherical adjoint approach,the vector equation of ΓPis

where(v1,v2,v3)are relative coordinates of P in{Rf;αf,nf,vf}of Cf.The first derivative of the vector equation of ΓPwith respect to σ is

In{RO;im,jm,km},point P can be regarded as adjoint to P0on Cm.The position vector of P is

where(u1,u2,u3)are relative coordinates of P in{Rm;αm,nm,vm}of Cm.Because point P is fixed on the moving body,its position in{RO;im,jm,km}does not change at all,or dRPm/dσ=0.Based on Eq.(9),coordinates(u1,u2,u3)meet the following spherical fixed point conditions:

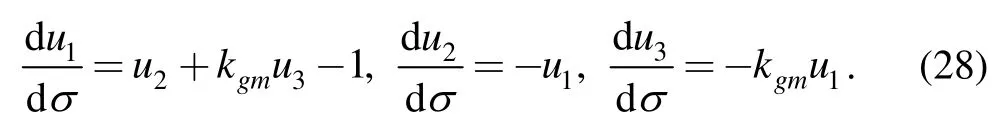
Because Eq.(24)holds true for the spherical moving and fixed centrodes at any instant,point P has the same relative coordinates and their change rates in the two Darboux frames of the centrodes.The condition equations are

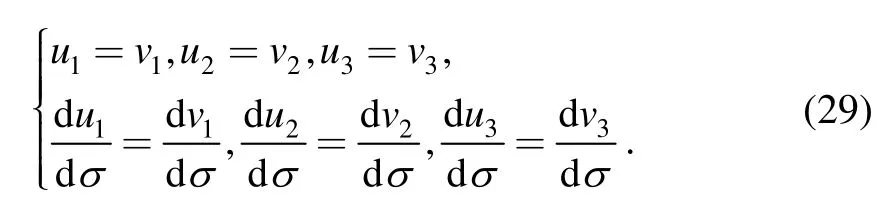
Substituting Eqs.(28)and(29)into Eq.(26),we can simplify the first derivative of the vector equation of ΓP,that is

Point P can also be described by coordinate parameters(δP,θP)in the Darboux frame,of which δPis angle between vectors RPand RP0,and θPis inclined angle of αfand projection vector of RPon coordinate plane Rf-αfnf.The relative coordinates of P in{Rf;αf,nf,vf}are

Substituting above equation into Eq.(28),we obtain

The Darboux frame{RP;αP,nP,vP}of ΓPis set up as

The relationship between arc length σPof ΓPand σ of the centrodes can be deduced from first expression of above equation,that is dσP=kg*sinδPdσ.

The geodesic curvature of ΓPis

If kgPis replaced by reciprocal of geodesic curvature radius ρg,the above equation can be rewritten as

4.2 Curvature theories for spherical point-path

As shown in Fig.5,the geodesic curvature center OPof ΓPis located on the binormal vector vPwith a distance ρgto point P.The inclined angle δ of vectors RPand ROPmeets equation tanδ=ρg.Then Eq.(35)can be rewritten as

The above equation is the Euler-Savary analogue for spherical motion.

If kgPof ΓPis equal to zero at an instant,we have

A spherical curve of the moving body can be determined by the above equation at any instant,which is called spherical geodesic inflection curve.Any point on the curve will trace a spherical trajectory curve in{RO;if,jf,kf},which contacts a great circle on the unit sphere to the second order.

The first derivative of kgPwith respect to σ can be derived through Eq.(34).By letting dkgP/dσ=0,we can obtain the condition equation as

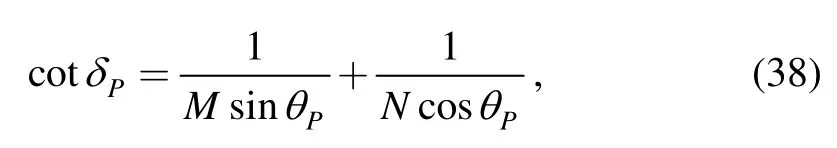
where

The above equation corresponds to a spherical curve at an instant,which is called spherical cubic of stationary curvature.The spherical path traced by any point on the curve contacts a spherical circle to the third order.

Letting kgP=0 and dkgP/dσ=0 hold true simultaneously,we obtain the intersection points of the spherical geodesic inflection curve and the spherical cubic of stationary curvature,which are called spherical Ball points.The spherical Ball points can be located through Eqs.(37)and(38).Combining the two equations,we have

where

Eq.(39)has eight solutions for the parameter δPand then eight spherical Ball points can be determined.But due to the symmetry of spherical motion,each spherical Ball point has the corresponding symmetrical one among the eight points about the sphere center.It means at most four spherical Ball points can be found at any instant.

By taking the second derivative of kgPwith respect to σ and letting it be zero,we have

At any instant,the parameters M,N and their derivatives have definite values,and not more than six values of θPcan be solved through the above equation.The points,whose parameters δP,θPmeet Eqs.(38)and(40)simultaneously,are called spherical Burmester points.The spherical path traced by any spherical Burmester point contacts a spherical circle to the fourth order.

If the parameter θPof point P is zero at an instant,P locates on the coordinate plane Rf-αfnf.Through Eq.(33),the Darboux frame{RP;αP,nP,vP}of ΓPis

The above equation indicates that vectors nP,vPboth lie on the common tangent plane Rf-αfnfof the moving and fixed axodes.The normal of the point-path ΓPis also located on the plane and tangent to the axodes.Based on the relational expression kP2=knP2+kgP2,the normal of ΓPperpendicular intersects with the ISA at point OP,which is just the curvature center of ΓP,as shown in Fig.6.

In particular,the base cone of an involute bevel gear is regarded as the fixed axode and the generating plane is taken as the moving axode.With the rolling of the generating plane on the base cone without sliding,a point P on the generating plane traces a spherical curve ΓP,which is just the spherical involute and has the analogue properties to the plane involute.Based on the spherical adjoint approach,the geometric properties of the spherical involute can be studied.For the meshing of two spherical involute bevel gears with spherical involute as the tooth curve,the transmission characteristics can be reflected by the two axodes-pitch cones,as shown in Fig.7.Thereby,based on the axodes,the meshing principle of the spherical involute bevel gear,similar to that of involute cylindrical gear can be developed.The general conjugation model for planar gearing transmission[32]can also be extended to spherical gearing transmission by the axode-based adjoint approach.

Fig.7 Meshing of two spherical involute bevel gear

5 Curvature Theory for a Plane in Spherical Motion

5.1 Vector equation and construction parameters of the plane-envelope

In this section,the spherical centrodes are still adopted to study the geometrical properties of the plane-envelope.

As shown in Fig.8,a plane T of the rigid body in spherical motion can be described by the unit normal vector n and the distance e from the sphere center O to the plane.The perpendicular from O to the plane intersects it at point P,whose position vector is

where(n1,n2,n3)are relative components of n in{Rf;αf,nf,vf}and there exists a relational expression n12+n22+n32=1.

With the spherical motion of the rigid body,T traces a family of planes in{RO;if,jf,kf}.By taking Cfas original curve and T as adjoint plane,we can write the vector equation of the family of planes as

where(a1,a2,a3)are the relative coordinates of any point on T in{Rf;αf,nf,vf}.The first derivative of n with respect to σ is

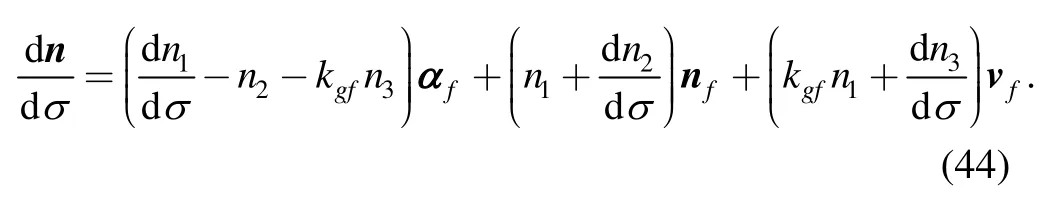
On the other hand,Cmcan be visualized as the original curve to describe the adjoint motion of T in{RO;im,jm,km}.Since T is inscribed in the moving body,the fixed plane condition dnm/dσ=0 should be satisfied.Based on Eq.(44),we have

Combining Eqs.(44)and(45),we have

For the family of planes,the envelope surface Slshould meet the following equations:

At any instant,a straight line L is determined by Eq.(47).It is the intersection line of two consecutive trajectory planes.Slis naturally a ruled surface with L as the generatrix.Through Eq.(47),the unit vector l of L is

The position vector RPof point P meets Eq.(47),so P lies on the generatrix L.The trajectory ΓPof P can be viewed as directrix of Sland the vector equation of Slis

The distance between the striction curve and the directrix of Slalong L,or striction directrix distance for short,is

The vector equation of the striction curve of Slis

The Frenet frame{ρl;E1,E2,E3}of Slis set up as

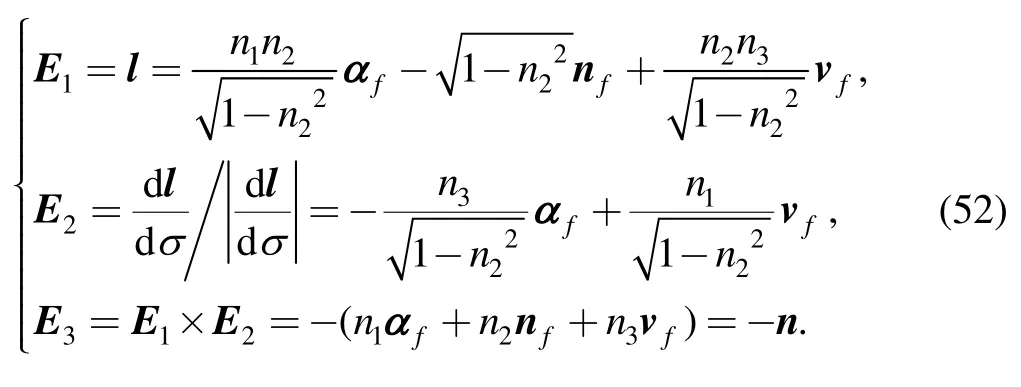
Based on the differential formulas of the Frenet frame,the construction parameters of Slare

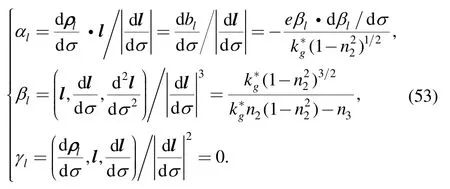
The construction parameters αl,βland γlare the kinematic invariants of Sland totally determine its geometrical properties[12].The distribution parameter γlof Slis zero confirms that Slis developable.Then Slcan only be a cylindrical surface,a cone,or a tangent surface.The characteristics of Sl,such as the contact or approximating conditions of Sland some specific developable ruled surfaces,can be revealed by αl,βland their derivatives.

5.2 Geometrical characteristic of the plane-envelope

5.2.1 Circular cylindrical surface

βlis the geodesic curvature of the spherical image curve of the generatrices of Sl.If βltends to infinity,a cusp exists on the spherical image curve.The three consecutive generatrices of Slare parallel.Through Eq.(53),the condition equation is

The unit normal vector n can also be described in{Rf;αf,nf,vf}by the parameters(δn,θn),of which δnis the angle between n and RP0,and θnis the inclined angle of αfand the projection vector of n on plane Rf-αfvf.A group of parallel planes are obtained through Eq.(54)at any instant.With the spherical motion of the rigid body,the three consecutive trajectory planes traced by any of the parallel planes are all tangent with a circular cylindrical surface.In particular,if the radius of the circular cylindrical surface is zero,the three consecutive trajectory planes intersect at a common straight line,which becomes a stationary generatrix of the plane-envelope.

For the osculating circular cylindrical surface of the plane-envelope,the direction vector of the axis is of course l and the position of the axis can be determined by a point A on it,whose position vector is RAin{RO;if,jf,kf}.A function f(σ)={RP－RA－[(RP－RA)·l]l}2－r2is defined to describe the deviations of the radius r of the circular cylindrical surface and the distances from the tracing plane to the axis.The condition equations f(σ)=df(σ)/dσ=d2f(σ)/dσ2=0 must be satisfied by the osculating circular cylindrical surface.Based on Eqs.(42)and(46),the radius r can be derived as e.It means the point A is coincident with the sphere center O.If a plane in spherical motion passes through the rotation center and the normal vector satisfies Eq.(54),the three consecutive trajectory planes intersect at a common line.

If the parameters δPand θPin Eqs.(37)and(38)are replaced by δn,θn,and the two equations are concurrently satisfied by the normal vector n of a plane in spherical motion,the four consecutive trajectory planes will be tangent with a circular cylindrical surface.At most four sets of such parallel planes can be located in the moving body.

5.2.2 Circular conical surface

When the three consecutive trajectory planes of the tracing plane in spherical motion tangentially contact with a circular conical surface along a generatrix,αlof the envelope ruled surface should be equal to zero[29].Through Eq.(53),we have

The condition e=0 indicates that the tracing plane passes through the rotation center.If this condition is not satisfied,the normal vector of the plane should meet Eq.(38)only with the parameters δP,θPreplaced by δn,θn.The vertex of the circular conical cone is just the striction point of the envelope surface at the instant.The direction vector of the axis is

When the four consecutive trajectory planes of the tracing plane tangentially contact with a conical surface,the construction parameters of the plane-envelope need to meet condition equations αl=dαl/dσ=0,which are

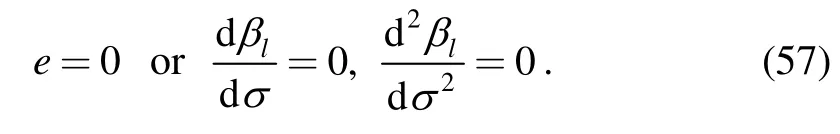
More strictly,if the conical surface is requested to be circular conical surface,the condition equations are αl=dαl/dσ=0,dβl/dσ=0.Through Eq.(53),we have

6 Kinematic Property of Spherical Four-Bar Linkage

6.1 Spherical adjoint motion of coupler link

A spherical four-bar linkage consists of four connecting rods,which can be viewed as segments of great circle on a spherical surface with radius R.The length of the connecting rod is defined by the central angle of the corresponding great circular arc.A spherical four-bar linkage ABCD is given in Fig.9 and the dimensions of the driving link AB,coupler link BC,driven link CD and the frame link AD are respectively l1,l2,l3and l4.The fixed Cartesian coordinate system{RO;if,jf,kf}is established on AD with the coordinate plane RO-ifkfcoplanar with plane OAD.The moving Cartesian coordinate system{RO;im,jm,km}is set up on BC with the coordinate vector kmcoaxial with the axis OB of the revolute pair and coordinate plane RO-jmkmcoplanar with plane OBC.The input rotation angle φ of link AB around axis OA is defined by the dihedral angle of plane OAB and plane OAD,while the rotation angle ψ of link BC around axis OB is defined by the dihedral angle of plane OBC and plane OAB.

For the spherical linkage,the axis OB of the revolute pair traces a cone,which intersects the spherical surface at a spherical curve ΓBin{RO;if,jf,kf}.The vector equation of ΓBis

The coupler point is always adjoint to the axis OB with the motion of the coupler link.The cone traced by OB is logically taken as original ruled surface to study the geometrical properties of coupler curve.The Darboux frame{RB;αB,nB,vB}of ΓBis set up as

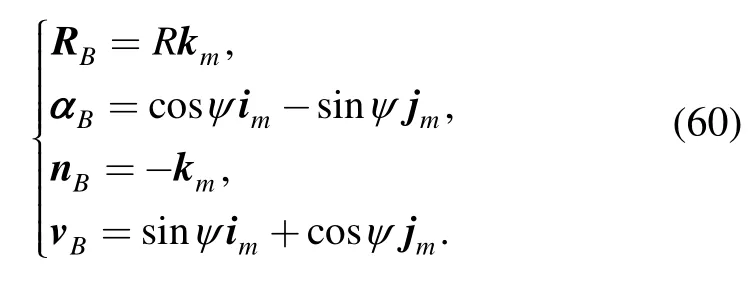
A coupler point P with spherical coordinates(R,ξP,ηP)in{RO;im,jm,km}traces a spherical coupler curve ΓPin{RO;if,jf,kf}.The vector equation of ΓPcan be written as

where(uP1,uP2,uP3)are the relative coordinates of P in{RB;αB,nB,vB}.They are

6.2 Moving and fixed spherical centrodes

For the spherical four-bar linkage,the angle θ in Eq.(6)is 2π-ψ.Based on Eq.(11),the position parameters of the velocity center P0of the coupler link meet

where the variable with a prime represents the derivative with respect to the arc length σBof ΓB,and similarly hereinafter.

During the motion period of the linkage,P0traces the spherical fixed centrode Cfin the frame link and the spherical moving centrode Cmin the coupler link.The vector equation of Cfis

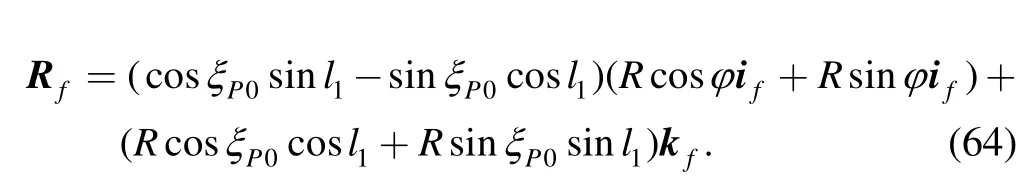
The geodesic curvature kgfof Cfis

The vector equation of Cmis

The geodesic curvature kgmof Cmis

The induced geodesic curvature kg*can be deduced by subtracting Eq.(67)from Eq.(65),that is

The link lengths of the spherical four-bar linkage on the unit sphere are designated as l1=π/6,l2=π/4,l1=π/3,l4=π/12.We can calculate the coordinates of the velocity center in{RO;if,jf,kf}and{RO;im,jm,km}by Eqs.(64)and(66)at any instant.The spherical centrodes Cmand Cfcan be drawn in Fig.10.At the instant φ=π/2,Cmand Cftangentially contact at the spherical instant center P0,which has the spherical coordinates(ξP0=0.970 7,ηP0=5.552 8)in{RO;im,jm,km}and Cartesian coordinates(0,－0.432 4,0.901 7)in{RO;if,jf,kf}.Through Eqs.(65)and(67),the geodesic curvatures kgfof Cfand kgmof Cmare respectively 2.495 9 and 1.102 3.Then the induced geodesic curvature kg*is 1.393 6.

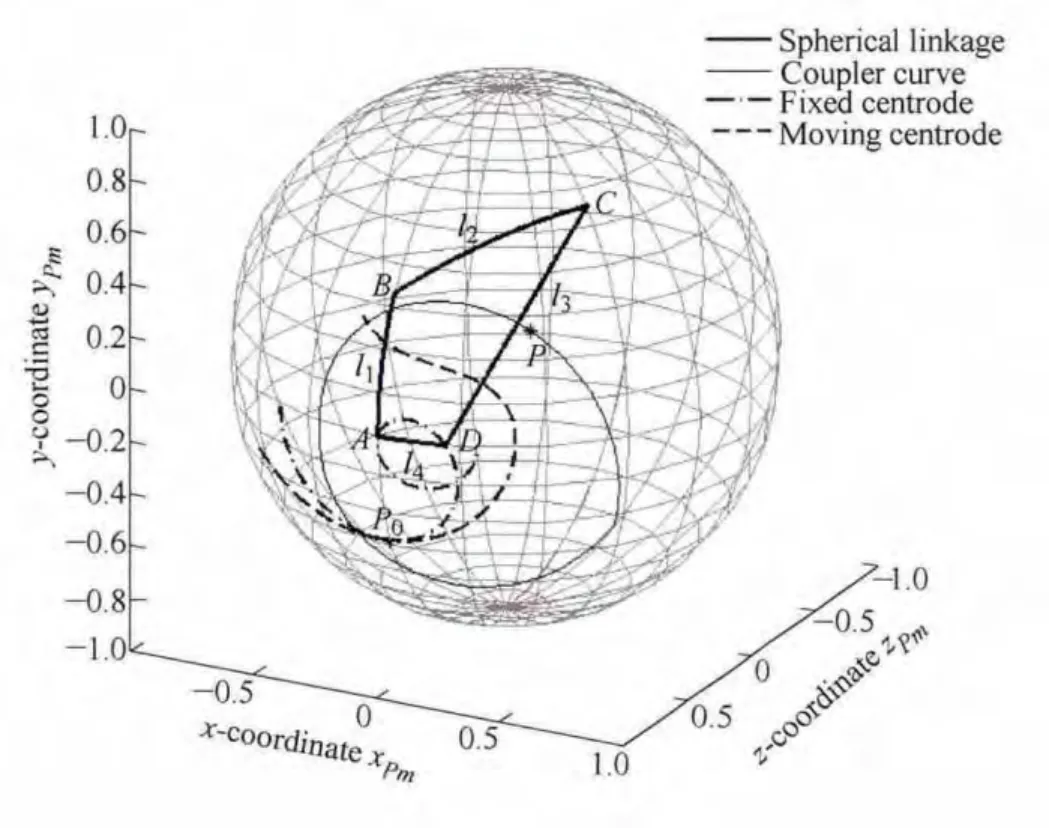
Fig.10 Spherical centrodes and coupler curve

6.3 Spherical geodesic inflection curve and ball curve

For the coupler point P with Cartesian coordinates(0.353 6,0.353 6,0.866 0)in{RO;im,jm,km},the spherical trajectory curve ΓPis depicted in Fig.10.The parameters(δP,θP)of point P in{Rm;αm,nm,vm}of the moving centrode are(1.033 6,0.846 6).Through Eq.(34),the geodesic curvature kgPof ΓPat φ=π/2 is 1.323 8.We have the following Euler-Savary equation:

When the rotation angle of the driving link AB is 2.5,the induced geodesic curvature kg*of the centrodes is 1.686 9.Based on Eq.(37),the equation of the geodesic inflection curve Γ1in the coupler link is

The geodesic inflection curve Γ1is drawn in Fig.11.

Similarly,when the rotation angle of the driving link is 3.1,the induced geodesic curvature is 2.181 0.The spherical geodesic inflection curve Γ2in Fig.11 has two branches.One branch is a closed curve,which starts from point P0and closes at point P1(δP1=0.580 3,θP1=－π/2).Another branch is an open curve,which starts from point P2(δP2=0.990 5,θP2=－π/2).The Cartesian coordinates of points P1and P2in{RO;im,jm,km}are respectively(0.918 6,0.294 1,0.263 8)and(0.883 1,0.456 6,－0.108 0).

Fig.11 Geodesic inflection curves

At the instant φ=2.928 0,the induced geodesic curvature is 2.As shown in Fig.11,the spherical geodesic inflection curve Γ3crosses itself at point P3(δP3=π/4,θP3=－π/2).The Cartesian coordinates of P3in{RO;im,jm,km}are(0.960 7,0.275 8,0.031 7).

At any instant,at most four spherical Ball point can be located in the coupler link.When the rotation angle φ is π/2,kg*is 1.393 6.Based on Eqs.(37)and(38),the equations of the spherical Ball points in the coupler link are

Through the above equation,we obtain two spherical Ball points PB1and PB2,whose coordinates parameters in{Rm;αm,nm,vm}are(δPB1=1.798 4,θPB1=0.311 3)and(δPB2=1.885 7,θPB2=2.718 7)respectively.The Cartesian coordinates of PB1and PB2in{RO;im,jm,km}are(0.290 5,0.936 3,0.197 1)and(－0.918 2,－0.389 8,0.071 0).

7 Conclusions

(1)The spherical adjoint approach provides a reliable instrument to study the axodes-based curvature theories of a point and a plane in spherical motion.The intrinsic connections among the point-path or the plane-envelope and the axodes(spherical centrodes)are revealed based on the spherical fixed point and plane conditions.

(2)Based on the adjoint approach,the kinematic meaning of the induced geodesic curvature of spherical centrodes for spherical motion is present.The geometrical properties of the point-path and plane-envelope are examined,which include the Euler-Savary analogue for the point-path and the osculating conditions of the plane-envelope and the cylindrical surface or the circular conical surface.

(3)The curvature theories of general spherical motion are directly applied to the spherical four-bar linkage to locate the specific characteristic points of the coupler link.The approach introduced in this paper can also be adopted to study the mesh principle of spherical bevel gears.

[1]HUNT K H.Kinematic geometry of mechanisms[M].Oxford:Clarendon Press,1978.

[2]BOTTEMA O,ROTH,B.Theoretical kinematics[M].New York:North-Holland Press,1979.

[3]MCCARTHY J M.An introduction to theoretical kinematics[M].London:The MIT Press,1990.

[4]CHIANG C H.Kinematics of spherical mechanisms[M].Cambridge:Cambridge University Presss,1988.

[5]SKREINER M.A study of the geometry and the kinematics of instantaneous spatial motion[J].Journal of Mechanisms,1966,1(2):115–143.

[6]BOKELBERG E H,HUNT K H,RIDLEY P R.Spatial motion—I:points of inflection and the differential geometry of screws[J].Mechanism and Machine Theory,1992,27(1):1–15.

[7]RIDLEY P R,BOKELBERG E H,HUNT K H.Spatial motion—II:acceleration and the differential geometry of screws[J].Mechanism and Machine Theory,1992,27(1):17–35.

[8]STACHEL H.Instantaneous spatial kinematics and the invariants of the axodes[C]//Proceedings of A Symposium Commemorating the Legacy,Works,and Life of Sir Robert Stawell Ball Upon the 100th Anniversary of A Treatise on the Theory of Screws,2000,July 9–11:1–14.

[9]DISTELI M.Über das analogon der savaryschen formel und konstruktion in der kinematischen geometrie des raumes[J].Zeitschrift für Mathematic und Physik,1914,62:261–309.

[10]DOONER D B,GRIFFIS M W.On spatial euler-savary equations for envelopes[J].ASME Journal of Mechanical Design,2006,129(8):865–875.

[11]SCHUTTER J D.Invariant description of rigid body motion trajectories[J].ASME Journal of Mechanisms and Robotics,2009,2(1):011004.1–011004.9.

[12]SASAKI S.Differential geometry[M].Tokyo:Kyolitsu Press,1956.(in Japanese)

[13]DOBROVOLSKII V V.On spherical coupler curves[J].Prikl.Mat.Mekh.,1947,8(6):475–477.(in Russian)

[14]CAPELLEN M W,DITTRICH G,JANSSEN B.Systematik und kinematik ebener und sphärischer viergelenkgetriebe[M].Köln und Opladen:Westdeutscher Verlag,1966.

[15]MULLER H R.Sphärische kinematik[M].Berlin:VEB-Verlag der Wissenschaften,1962.

[16]VELDKAMP G R.An approach to spherical kinematics using tools suggested by plane kinematics[J].Mechanism and Machine Theory,1967,2(4):437–450.

[17]KAMPHUIS H J.Application of spherical instantaneous kinematics to the spherical slide-crank mechanism[J].Journal of Mechanism,1969,4(1):43–56.

[18]YANG A T,ROTH B.Higher order path curvature in spherical kinematics[J].ASME Journal of Engineering for Industry,1973,95(2):612–616.

[19]SODHI R,SHOUP T E.Axodes for the four-revolute spherical mechanism[J].Mechanism and Machine Theory,1982,17(3):173–178.

[20]DOWLER H J,DUFFY J,TESAR D.A generalized study of three multiply separated positions in spherical kinematic[J].Mechanism and Machine Theory,1976,11(6):395–410.

[21]DOWLER H J,DUFFY J,TESAR D.A generalized study of four and five multiply separated positions in spherical kinematic—II[J].Mechanism and Machine Theory,1978,13(4):409–435.

[22]MCCARTHY J M.The differential geometry of curves in an image space of spherical kinematics[J].Mechanism and Machine Theory,1987,22(3):205–211.

[23]TING K L,BUNDUWONGSE R.Unified spherical curvature theory of point-,plane-,and circle-paths[J].ASME Journal of Mechanical Design,1991,113(2):142–149.

[24]TING K L,SONI A H.Instantaneous kinematics of a plane in spherical motion[J].ASME Journal of Mechanisms,Transmissions,and Automation in Design,1983,105(3):560–567.

[25]CHEN J S,CHIANG C H.On the coupler-great-circle envelopes of spherical four-bar linkages[J].Mechanism and Machine Theory,1988,23(5):393–399.

[26]CHIANG C H.Spherical kinematics in contrast to planar kinematics[J].Mechanism and Machine Theory,1992,27(3):243–250.

[27]FU T T,CHIANG C H.Simulating a given spherical motion by the polode method[J].Mechanism and Machine Theory,1994,29(2):237–249.

[28]WANG Delun,LIU Jian,XIAO Dazhun.A unified curvature theory in kinematic geometry of mechanism[J].Science in China(Series E)1998,41(2):196–202.

[29]WANG Delun,LIU Jian,XIAO Dazhun.Geometrical characteristics of some typical spatial constraints[J].Mechanism and Machine Theory,2000,35(10):1413–1430.

[30]MOZZI G.Discorso matematico sopra il rotamento momentaneo dei corpi[M].Napoli:Stamperia di Donato Campo,1763.

[31]CHASLES M.Note sur les proprietes generales du systeme de deux corps semblables entr’eux[J].Bullettin de Sciences Mathematiques,Astronomiques Physiques et Chimiques,Baron de Ferussac,Paris,1830:321–326.

[32]DONG Huimin,TING K L.Differential contact path and conjugate properties of planar gearing transmission[J].ASME Journal of Mechanical Design,2012,134(6):06010.1–06010.11.