基于自适应阈值的curvelet医学超声图像去噪算法

庄哲民，姚伟克，杨金耀，李芬兰，袁 野

1 汕头大学电子工程系，汕头市，515065

2 汕头市超声仪器研究所有限公司，汕头市，515000

基于自适应阈值的curvelet医学超声图像去噪算法

【作者】庄哲民1，姚伟克1，杨金耀2，李芬兰1，袁 野1

1 汕头大学电子工程系，汕头市，515065

2 汕头市超声仪器研究所有限公司，汕头市，515000

传统的超声图像去噪算法在抑制斑点噪声的同时，会丢失图像中的大量细节和微弱的边缘信息。该文基于curvelet变换提出一种新的自适应阈值去噪声算法，该算法利用各层curvelet系数局部方差在超声图像纹理与平滑度的差异，分别定义模糊区域和隶属度函数，并根据隶属度函数确定相关curvelet系数的自适应阈值，通过该阈值实现对超声图像的去噪。实验测试表明，该方法在保留原有图像细节信息的基础上有效地降低了超声图像的斑点噪声，极大地提升B超仪器的性能。

超声图像；斑点噪声；去噪；curvelet变换；自适应阈值

0 引言

超声诊断相较于其它的医学影像诊断，具有简单、安全、有效、重复性强、价格低等特点，因此超声诊断已经成为医学临床诊断的重要手段之一。在超声成像中，当人体组织的结构尺寸与入射超声波波长相近或小于波长时，超声束发生散射，相位不同的散射回波相互干涉产生斑点噪声，以至于图像对比度低，给超声图像的后期处理带来很大的困难[1]。由于在超声诊断中主要依靠丰富经验的医生靠肉眼来对超声图像进行判断，然而B超图像中的斑点噪声不仅降低超声图像中进行病灶分割和匹配的速度与准确率，而且严重影响医生对正常和病变组织的识别能力。

由于超声图像噪声主要是以斑点噪声的形式出现，斑点噪声是一种与图像信号无关的乘性噪声，其存在使得超声图像信噪比低，图像变得模糊不清。斑点噪声主要分布在高频部分，而超声图像的一些重要特征信息如边缘、纹理等细节信息也是位于高频部分，传统滤除高频部分噪声的方法大多针对的是加性噪声，会对图像的相关细节信息造成破坏，并不适用于超声图像去噪。因此针对超声图像去噪具有的特殊性与难度，在进行相关去噪的同时应尽可能地保留图像边缘信息，在不降低图像的分辨率的前提下，最大限度的抑制斑点噪声是超声图像去噪的目标。

现有去除斑点噪声的算法大体分为三类：一是空间域局部统计滤波算法（Lee滤波和Kuan滤波）[2]，该类算法主要是基于中心像素及周围像素的统计关系进行的，窗口尺寸越大就越平滑，在一些具有复杂结构的图像中很难在平滑和保留细节之间寻找到平衡；二是各向异性扩散滤波算法（PM模型）[3]，PM模型主要运用图像梯度的单调减函数来表示扩散系数，而由于含噪图像中梯度具有很大的不稳定性，会随着图像的平滑程度的增加而下降，因此在去噪效果上并不理想；三是基于多尺度变换的滤波算法（小波）[4]，二维小波变换的基是各向同性的，无法很好地表达边缘的信息，这就使得传统小波变换在处理二维图像时表现出一定的局限性。Candes等在1998年提出一种新的多尺度变换方法，即Ridgelet变换，对于具有超平面奇异性的高维多变量函数具有良好的逼近能力，能够有效地处理高维信号的奇异性，较好地实现对此类信号的逼近。随后Candes和Donoho等又在Ridgelet变换的基础上提出了curvelet变换，相对于小波变换这一多尺度分析工具，curvelet变换的最大特点是具有高度的各向异性，因此具有更强的表达图像中沿边缘信息的能力，其各向异性特征非常有利于图像边缘的高效表示，因此利用curvelet变换对超声图像进行相关去噪具有独特的优势。

1 curvelet去噪算法

Candes和Donoho在Ridgelet变换的基础上提出了curvelet变换并且构造了curvelet的紧框架，对于具有光滑奇异性曲线的目标函数，curvelet提供了高效、稳定以及接近最优的表示，相对于小波变换而言其最大特点是具有高度的各向异性，是一种具有方向性、带通、多分辨的函数分析方法。curvelet变换直接以边缘为基本表示元素，并且是各向异性的，具有很强的方向性，非常有利于图像边缘的高效表示[5]。从概念上讲，curvelet变换是多尺度金字塔的，它在每个尺度有很多方向和位置元素，而这些元素的几何多尺度特性使它与传统的像小波这样的多尺度表示法隔离开，新框架直接从频域进行多尺度分析，不再依赖这些几何特性。新的curvelet框架直接从频域进行分析，不再通过脊波变换实现，被称为第二代curvelet变换。

由文献[6]可知，curvelet变换可表示为：

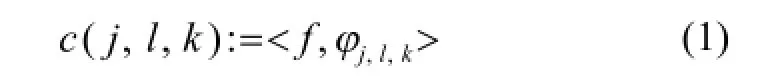
并且其离散curvelet系数可表示如下：

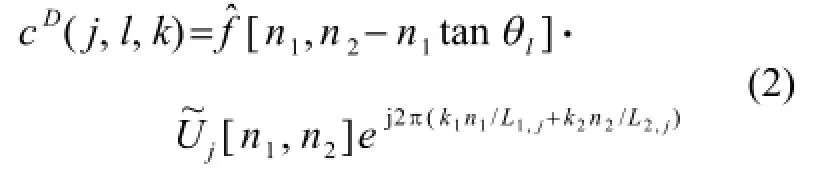
该离散curvelet系数cD( j, l, k)可以被划分成Coarse层、Detail层和Fine层三个部分。从频率分布上看，Coarse层是由低频系数组成，包含了图像的概貌；Detail层是由中高频系数组成，主要包含的是边缘特征；Fine层是由高频系数组成，体现的是图像的细节、边缘特征。由curvelet系数的分布和超声图像斑点噪声分布在高频部分的特点可以知道，基于curvelet变换去噪的重点在于如何选取一个合适的阈值对Detail层和Fine层的系数进行处理，尽可能去除噪声同时又保证超声图像的细节信息不被破坏。

2 基于自适应模糊阈值的curvelet去噪算法

阈值的确定是本文去噪算法的关键问题，合适的阈值应能够兼顾平滑（去除噪声）和拟合（与原始图像的近似程度）两方面的要求。当选取的阈值过大时，虽然能有效地去除噪声，但会产生过多的零系数，这样便破坏了原始图像的奇异性结构，造成伪影和模糊；当选取的阈值过小时，虽然会更好地和原始信号接近，但去噪又变得不彻底。传统curvelet去噪算法的阈值确定，往往需要未受噪声干扰的图像信息，或者估计噪声的方差，这些信息可以通过多次实验分析得到，但在实际应用中就有一定的局限性。因此根据图像和噪声经过curvelet分解后，在不同尺度和方向的系数的不同特点，本文提出一种基于自适应模糊阈值的超声图像去噪算法。

本文借鉴Shark[7]提出的模糊小波阈值去噪的方法，并结合局部方差确定模糊区域，再确定其阈值进行去噪。局部方差大则表示是在图像的边界、纹理等突变点上，信号对其有主要的影响，局部方差小则表示在图像的平滑区域，噪声对其有主要的影响[8]。

模糊性是指事物在形态及类属方面有不明确性，其根源在于各类相似的事物之间的变换是连续的，是由一系列的渐进过渡形成的，不是断续的，无联系的。这些过渡形式互相渗透，互相贯通，使得两个不同但相似的概念间没有明确的分界线。

所谓给定了论域U上的一个模糊子集A是指：对任何u∈U，都指定了一个数uA(u)∈[0, 1]与之对应，称uA(u)为u对A的隶属度。这意味构造一个映射：

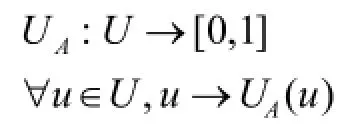
这个映射称为其模糊子集的隶属度函数。

首先，利用Donoho提出的多尺度统一阈值去噪方法，得到阈值

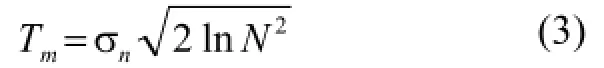
其中N2为第m层的信号长度，噪声方差可以用中值估计法得到即

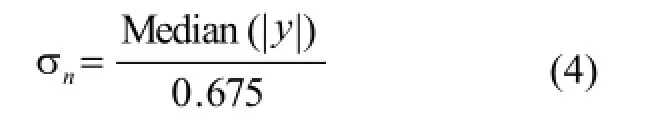
其中y为该层的curvelet系数，并构建一个阈值区域[CTm, Tm]其中C∈(0, 1)。然后根据文献[9]求出其各层系数的边缘标准差

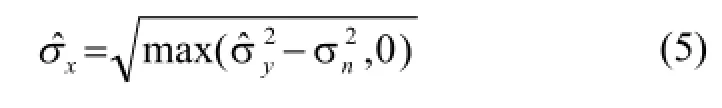
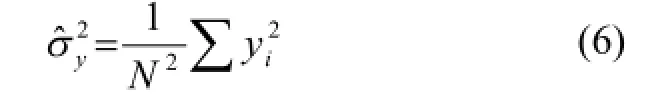
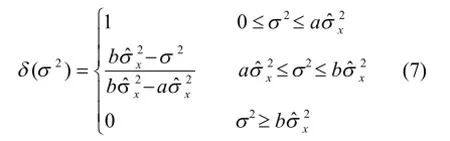
其中σ2为局部方差，a, b为常量。

局部方差将采用文献[9]的方法，其表达式为：

其中Zi,j是以(i, j)为中心的移动窗，L为奇数。

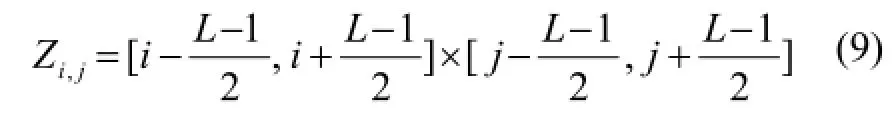
最后根据隶属度，可确定其自适应阈值为：

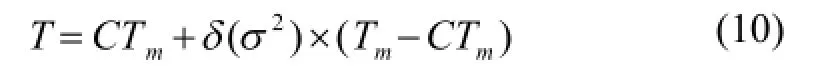
当隶属度δ(σ)2较小时其局部方差越大，此时在图像的边界、纹理等突变点上，信号对其有主要的影响，相应的阈值较小；而当隶属度δ(σ)2较大时其局部方差小，此时图像的平滑区域，噪声对其有主要的影响，相应的阈值较大。这样，通过隶属度确定的自适应阈值可以尽可能的滤除噪声，同时又能保留较多的细节信息。

本文的去噪算法过程如下：首先对含噪的超声图像进行curvelet变换可得到curvelet系数cD( j, l, k)；由于噪声主要分布在系数的Detail和Fine层，我们在Detail层和Fine层构建阈值区域结合局部方差确定其隶属度函数，确定各层各系数的阈值；接着使用软阈值处理规则对各系数进行处理确定最后的curvelet系数；最后将处理后的curvelet系数进行curvelet反变换，得到去噪后的超声图像。

3 实验结果及分析

为验证算法效果，本文使用临床超声图像进行仿真实验。在实验测试中，我们采用某进口高档B超仪器获取B超图像作为参考标准，如图1(a)所示；以较低档的B超仪器获取图像进行斑点噪声处理，如图1(b)所示;下面我们分别使用中值滤波、小波、基于curvelet的硬阈值处理和本文提出的基于curvelet的自适应阈值算法对超声图像进行去噪，从而对各算法进行比较，测试结果如图1(c)至图1(f)所示。

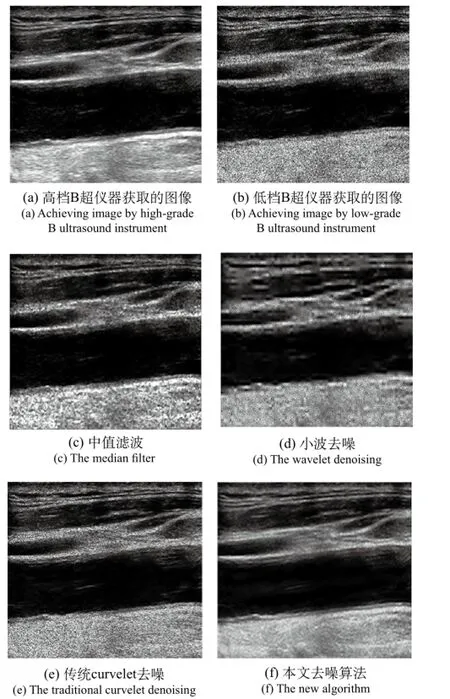
图1 颈动脉超声图像Fig.1 Carotid artery ultrasound image

从图中1(c)可以看出，中值滤波的去噪效果并不明显，中值滤波的性能受滤波窗口的影响较大，当滤波窗口较小时能较好地保护图像的边缘信息，但去噪能力受到抑制，而当滤波窗口增大时虽能较好地去除噪声，但会破坏图像的边缘信息；小波去噪的原理就是在小波分解结构中保留低频分量，对高频分量进行量化处理，在新生成的保留低频分量和量化后高频分量的分解结构图的基础上，再利用小波重构算法进行图像重构。但是二维小波变换的基是各向同性的，变换系数的局部模极大值只能反映出这个小波系数出现位置是“过”边缘的，而无法表达“沿”边缘的信息。由图1(d)可看出小波算法造成图像边缘模糊，损失大量细节，这就使得传统小波在图像去噪时具有一定的局限性。curvelet变换可以较好地解决小波只能恢复含水平和垂直方向的噪声图像这一局限性，但传统的curvelet的去噪算法如硬阈值法、软阈值法、块阈值法的关键问题在于选择合适的阈值，其决定着图像的去噪效果。从图1(e)中可以看出，传统的curvelet的去噪算法虽较好地保留下了图像的边缘，但去噪效果也并不显著；而从图1(f)可以看出本文提出的基于curvelet变换的自适应阈值去噪算法，能够解决传统curvelet去噪算法在阈值确定上往往需要未受噪声干扰的图像信息，或者估计噪声的方差这一局限性，具有更好地实际应用意义。

为了更好地定性与定量评估本文算法的性能，我们将低档B超仪器获取的超声图像（图1(b)）加入不同程度的斑点噪声，并用四种算法对其进行去噪，并通过定义峰值信噪比（Peak Signal to Noise Ratio, PSNR）对四种去噪算法进行比较。

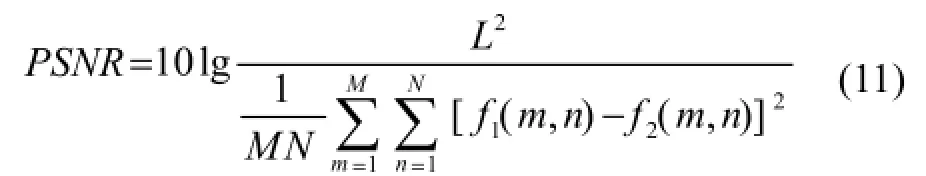
其中，L表示图像量化级数，PSNR的值越大，就说明算法的去噪效果越好。

比较结果如下表所示，VAR表示的是加入斑点噪声的方差，VAR=0表示低档B超仪器获取的超声图像（图1(b)），而VAR=0.2，VAR=0.4则分别是在VAR=0的图像上加入不同噪声方差而获得的图像。

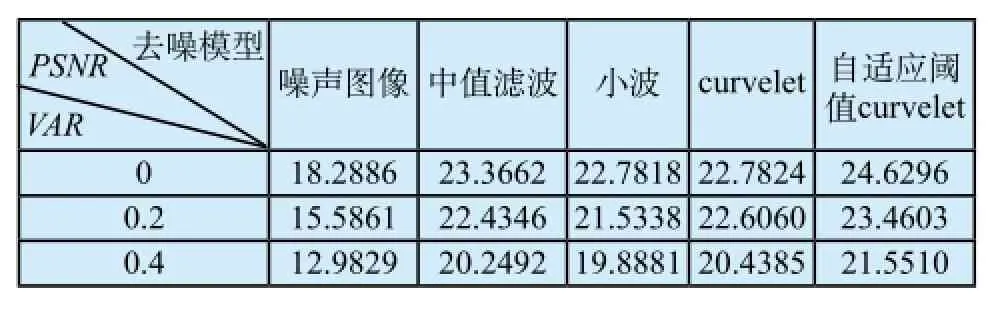
表1 各去噪算法去噪性能比较Tab.1 The denoising performance comparison with each algorithm

从表1可以看到，不同的去噪算法都能够较好的提高带噪声超声图像的PSNR，而随着噪声的增加，去噪后的图像PSNR也逐渐减小。由于小波造成图像边缘模糊，因此其PSNR在四种算法中较低，去噪效果较差。相比于中值滤波、小波和传统的curvelet算法，本文提出的基于curvelet的自适应阈值去噪算法的PSNR有一定程度的提高，也说明了本文算法在超声图像的去噪效果上具有较明显的优势。

4 总结

为改善传统医学超声图像去噪算法容易丢失边缘和纹理等细节信息这些缺点，本文提出了一种基于curvelet变换的自适应阈值的超声图像去噪声算法。该算法利用curvelet系数局部方差在超声图像纹理与平滑度的差异，结合模糊数学中的模糊区域和隶属度函数的概念确定各curvelet系数的自适应阈值，从而实现对超声图像的去噪。经实验表明本文算法在医学超声图像斑点噪声的抑制上有良好的效果，且具有较好的主观视觉，可以改善低档B超仪器在获取超声图像时带有较大斑点噪声的缺点，具有实际的应用意义。

[1] 乔蕊, 侯燕. 医学超声图像有效去噪方法研究与仿真[J]. 计算机仿真, 2013, 30(5): 391- 394.

[2] Zhong H, Zhang J, Liu G. Robust polarimetric SAR despeckling based on nonlocal means and distributed Lee flter[J]. IEEE Trans Geosci Remot Sens, 2014, 52(7): 4168-4210.

[3] Ham B, Min D, Sohn K. Revisiting the relationship between adaptive smoothing and anisotropic diffusion with modified flters[J]. IEEE Trans Imag Process, 2013, 22(3): 1096-1107.

[4] Quellec G, Lamard M, Cazuguel G, et al. Fast wavelet-based image characterization for highly adaptive image retrieval[J]. IEEE Trans Imag Process, 2012, 21(4): 1613-1623.

[5] Cand SE, Demanet L, Donoho D, et al. Fast discrete curvelet transforms[J]. Multiscal Model Simulat, 2006, 5( 3): 861- 899.

[6] Wang HZ, Qian LY, Zhao JT. An image denoising method based on fast discrete curvelet transform and total variation[C]. Int Conf Signal Process, 2010, 1040-1043.

[7] Shark LK, Yu C. Denoising by optimal fuzzy thresholding in wavelet domain[J]. Electronics lett, 2000, 36(6): 581-582.

[8] 关新平, 刘冬, 唐英干, 等. 基于局部方差的模糊小波阈值图像去噪[J]. 系统工程与电子技术, 2006, 28(5): 650-653.

[9] Abrahim BA, Kadah Y. Speckle noise reduction method combining total variation and wavelet shrinkage for clinical ultrasound imaging[C]. MECBME, 2011, 80-83.

Curvelet Denoising Algorithm for Medical Ultrasound Image Based on Adaptive Threshold

【Writers】Zhuang Zhemin1, Yao Weike1, Yang Jinyao2, Li FenLan1, Yuan Ye1
1 Department of Electronic Engineering，Shangtou University, Shangtou, 515065 2 Shantou Institute of Ultrasonic Instruments Co. Ltd., Shangtou, 515000

The traditional denoising algorithm for ultrasound images would lost a lot of details and weak edge information when suppressing speckle noise. A new denoising algorithm of adaptive threshold based on curvelet transform is proposed in this paper. The algorithm utilizes differences of coeffcients' local variance between texture and smooth region in each layer of ultrasound image to define fuzzy regions and membership functions. In the end, using the adaptive threshold that determine by the membership function to denoise the ultrasound image. The experimental text shows that the algorithm can reduce the speckle noise effectively and retain the detail information of original image at the same time, thus it can greatly enhance the performance of B ultrasound instrument.

ultrasound image, speckle noise, denoising, curvelet transform, adaptive threshold

TP391.41

A

10.3969/j.issn.1671-7104.2014.06.002

1671-7104(2014)06-0398-04

2014-04-09

国家自然科学基金面上项目（61070152）；广东省重大科技专项项目（2011A080404005）

庄哲民，E-mail: zmzhuang@stu.edu.cn