遗传阿贝尔范畴上twist Hall代数到2-周期复形Hall代数的嵌入
林 记
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
0 引言
设Q是一个不带循环圈的有限箭图,K=Fq是有限域,A是有限维代数KQ的有限生成模范畴,Q的底图决定了一个Cartan矩阵,设g=n+⊕⊕n-为相应的导出Kac-Moody李代数. Ringel[1]和Green[2]证明了从量子包络代数Ut(n+)到twist Hall 代数Htw(A)有一个单的代数同态;在该同态下,Ut(A)就与Htw(A)的由这些生成子生成的twist Hall子代数同构;同时,Green给出了余积的范畴构造。肖杰[3]给出了反极子,Ut(n+)的Hopf代数结构通过阿贝尔范畴A得到的twist Hall代数完全实现了出来.
一个自然的问题是如何给出整个量子群Ut(g)的一个代数实现?彭联刚和肖杰[4~5]通过对A的根范畴的讨论,实现了所有的可对称化的Kac-Moody李代数.对任意一个满足某些有限条件的微分分次范畴,To⊇n[6]定义了一个导出Hall代数,由与之相应的三角范畴的不变量给出了该导出Hall代数的结构常数的计算公式.肖杰和徐帆[7]简化了To⊇n的构造,并对有限域上的三角范畴直接给出了导出Hall代数的定义.
最近,Bridgeland[8]用2-周期复形构造了量子群Ut(G), 并建立了2-周期复形范畴的Hall代数DH(A)与extended Hall代数的Drinfeld double之间的联系.文章研究了遗传Abel范畴上的twist Hall代数到2-周期复形代数的嵌入,并找到了一种新的代数嵌入.
本文的主要结果如下:
定理1定义映射
I+∶Htw(A)→DH(A),[A]|→EA,
则I+是一个代数嵌入.
1 预备知识
在本节中,我们给出twist Hall代数和2-周期复形Hall代数的定义和基本性质[8~9].
在下文中,假设A是一个阿贝尔范畴且满足:A的对象是一个集合,对象之间的态射是有限维的,在k=Fq上面是线性的,并且A的全局维数有限,用A,B,C表示A的任意对象.
定义1.1Hall 代数H(A)以A的同构类为基元,乘法定义为

其中[A]表示A所在的同构类,其单位元为[0].
记K(A)为A的Grothendieck群,∈K(A)表示对象A∈A所在的类,K≥0(A)⊂K(A)表示由这些类构成的子集.对任意对象A,B∈A,定义

由此可得欧拉双线性型
<-,->∶K(A)×K(A)→Z(α,β)=(α,β)+<β,α>.
定义1.2Twisted Hall 代数Htw(A)的向量空间与H(A)相同,乘法定义为
[A]*[C]=t·[A]◇[C].
若在此基础上增加符号Kα和关系
Kα*Kβ=Kα+β,
Kα*[β]=t<α,β>.[B]*Kα
(1)
称之为extended Hall代数,记为Hetn(A).注意
{Kα*[B]|α∈K(A),B∈Iso(A)}构成了Hetn(A)的一组基元.
设CZ2(A)为由A上的Z2分次复形的构成的阿贝尔范畴,其对象如下所示
对象M.到N.的态射为s.∶M.→N.,使得
si↓s0↓
满足si+1·di=di'·Si.对于态射s.,t.∶M.→N.,如果存在态射hi∶Mi→Ni+1使得ti-si=d'i+1ohi+hi+1odi,我们就称s.,t.∶M.→N.是同伦的.对任意对象M.∈CZ2(A), 用M.表示M0-M1∈K(A).
记HoZ2(A)为CZ2(A)的同伦范畴,CZ2(P)⊂CZ2(A)表示投射复形构成的满子范畴.为方便,我们简记
C(A)∶=CZ2(A),C(P)=CZ2(P),
Ho(A)=HoZ2(A).

引理1.3[7]设M.,N.∈C(P),则有
ExtC(A)(N.,M.)≌HomHO(A)(N.,M.*).
对于M.∈C(A),若H*(M□),则称M.是零调的.对于任意对象p∈P, 记
则有如下结果:

设H(C(A))是由阿贝尔范畴C(A)定义的 Hall 代数;H(C(P))⊂H((A))由投射对象构成的子空间.对于H(C(P))两个对象M.,N.,定义乘法t
在此定义下,我们有如下的一些基本结论.
引理1.5[7]对于任意P∈P及M.∈C(P),在Htw(C(P))有
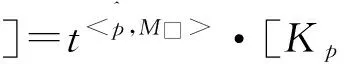

(2)

(3)
特别地, 对于P,Q∈C(P),有
[Kp]*[KQ]=[Kp⊕KQ],


定义1.6记DH(A)∶=Htw(C(P))[[M.]-1|H*(M□)=0],称之为Bridgend's Hall代数.
定义1.7记DHred(A)∶=DH(A)/([M□]-1∶H*(M□)=0,M.≌M.□) ,称之为Bridgend's Hall代数.

2 主要结果的证明
任取A∈A, 取极小投射分解

(5)
H1(CA)=0及CA=Q-P=A.
引理2.1任取A1,A2∈A,取极小投射分解
则有短整合列0→HomA(Q1,P2)→HomC(A)(CA1,CA2)→HomA(A1,A2)→0.
证明对任意的a∈HomA(A1,A2),存在a1,a2使得下图交换
若a=0,则存在唯一的b∈HomA(Q1,P1)使得a2=f2ob, 再由CA的定义可得结果.
令EA=t



以下给出定理1的证明.
任取A1,A2∈A,设
[A1]*[A2]=
取A1,A2的极小投射分解
易得A3有投射分解

所以有
I+([A1]*[A2])=t
(6)
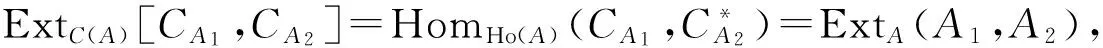

因此
I+(A1)*I+(A2)=t
t
(7)
其中n=
|HomC(A)(CA1,CA2)|=|HomA(A1,A2)|·
|HomA(Q1,P2)|.
所以对比(6)和(7),再由
可知I+([A1]*[A2])=I+([A1]*I+[A2])
成立当且仅当
n+2
由A1=Q1-P1,A2=Q2-P2易得上面等式成立.
显然,若[B1],[B2],…,[Bj](Bi∈A) 在A中线性无关,则[CB1],[CB2],…,[CBj] 在C(A)中线性无关,则[EB1],[EB2],…,[EBj]在DH(A)线性无关,所以I+是单的.
[1] RINGEL C.Hall algebras and quantum groups[J].Invent. Math,1990,101(3):583-591.
[2] GREEN J A .Hall algebras, hereditary algebras and quantum groups[J]. Invent. Math,1995,120(1): 361-377.
[3] XIAO J .Drinfeld double and Ringel-Green theory of Hall algebras[J].J. Algebra,1997,190(1):100-144.
[4] PENG L, XIAO J. Root categories and simple Lie algebras[J]. J. algebra, 1997,198 (1):19-56.
[5] PENG L, XIAO J. Triangulated categories and Kac-Moody algebras[J].Invent. Math, 2000,140(3):563-603.
[7] XIAO J,XU F . Hall algebra associated to triangulated categories[J].Duke Math. J., 2008,143(2): 357-373.
[8] BRIDGELAND T .Quantum groups via Hall algebras of complexes[J].Annals of Mathematics, 2013,177(2):739-759.
[9] SCHIFFMANN O .Lectures on Hall algebras[OL]. arXiv:0611617v2.

