中国高校R&D 投入与经济发展动态关系研究

张海英，周志刚，朱迎春

(1.天津大学管理与经济学部，天津 300072；2.沧州师范学院，河北 沧州 061001；3.中国科学技术发展战略研究院，北京 100038)

1 模型构建及数据来源

1988年Holtz-Eakin 在对美国劳动报酬和劳动时间之间动态关系的研究中，首次提出了面板数据的向量自回归(Panel Data Vector Autoregression，PVAR)方法。PVAR 模型可以表示为:

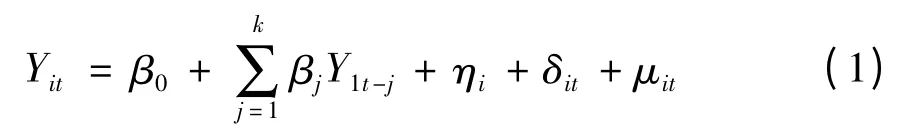
式中:i 表示省区;t 表示时间;j 表示滞后期数;Yit=(LnRDit，LnGDPit，STRit)T，表示第i 个省区第t年的3 ×1 维变量，该变量包括三个内生变量:高校R&D 经费投入、经济增长指标、产业结构指标，表示为LnRDit、LnGDPit、STRit;β0为常数向量;βj为滞后期系数矩阵;Yit-j表示滞后j 期的变量;ηi为省区间的固定效应向量，反映个体的异质性;δit为时间效应向量，表示同一时点的不同截面上可能受到的共同冲击;μit为随机误差效应向量。

本文用各省区高校R&D 支出表示高校研发投入指标，记作RD;用各省区的国民生产总值作为衡量经济增长的指标，记作GDP;经济发展中产业结构调整规律主要体现在三次产业比重的变化，第三产业的规模与质量对一国经济的发展具有重要意义，故以第三产业产值所占当年GDP 的比重表示产业结构调整程度，记作STR。RD、GDP、STR 的数据，分别来源于相关年度的《中国统计年鉴》、《中国科技统计年鉴》，时间跨度为1999—2011年，区域跨度为31 个省、直辖市、自治区。其中，STR 指标为两数的比值，表示产业结构的相对变化。为了便于比较，这里只对另外两项指标取对数得到LnRD、LnGDP，目的是通过对数变换，将高校R&D 投入和经济增长由水平量变化转换成相对量变化，同时增强变量之间的线性趋势，消除异方差。

2 实证分析

2.1 单位根检验

为了避免出现PVAR 模型的“虚假回归”或“伪回归”现象，保证估计的有效性，需要对变量进行平稳性检验。为了克服检验的局限性，保证结论的稳健性，本文利用Stata10 版对LnRD、LnGDP 和STR 分 别 进 行LLC、Breitung、ISP、Fisher-ADF、Fisher-PP、Hedri 平稳性检验。检验结果见表1，三个变量的水平值不能完全拒绝存在单位根假设。而三个变量的一阶差分序列在1%显著水平下均为平稳序列，故变量为一阶单整序列I (1)。

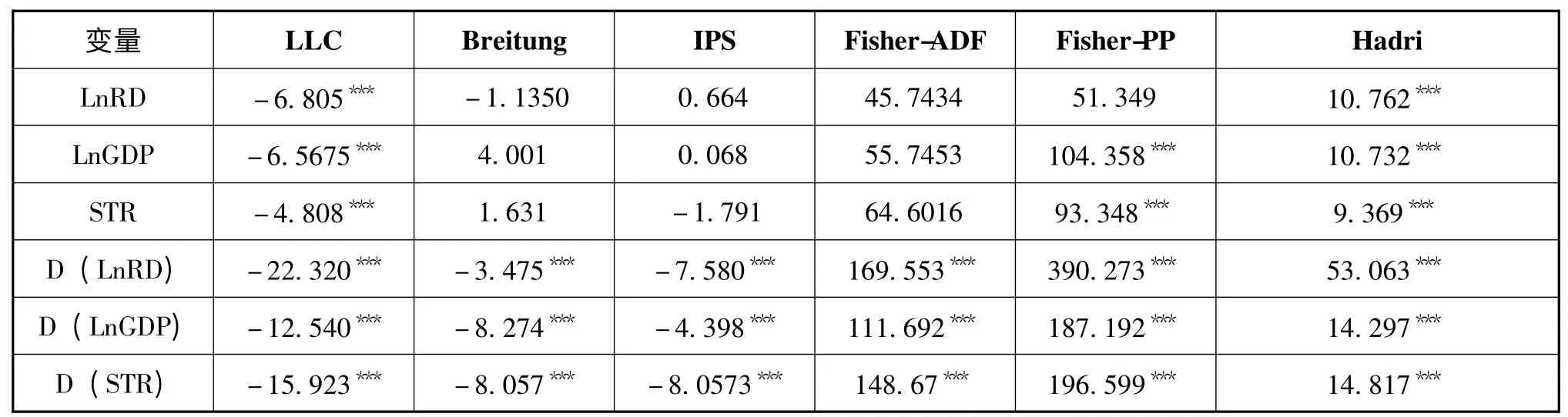
表1 lnGDP、lnRD 和STR 的单位根检验结果

2.2 PVAR 协整检验

在面板单位根检验的基础上，分别对高校R&D 经费投入与经济增长、高校R&D 经费投入与产业结构等面板数据之间是否存在协整关系进行检验，见表2。目前，常用的面板协整检验方法为基于残差的协整检验，包括同质面板协整检验如Kao 残差协整检验方法，和异质面板协整检验如Pedroni 残差协整检验方法。考虑到我国区域的异质性，本文选择Pedroni 残差协整检验法，根据残差检验的组内统计量Panel_ v、Panel _ rho、Panel_ PP、Panel_ ADF，组间统计量Group_ rho、Group_ PP、Group_ ADF 的显著性水平，以及Pedroni 的蒙特卡罗模拟实验显示的小样本条件下采用Panel_ ADF 和Group_ ADF、Panel_ PP 和Group_ PP 统计量更优的原则。我们可以综合判断，1999—2011年间，高校研发投入与经济增长之间存在着长期协整关系，而高校研发投入与产业结构之间不存在长期协整关系。故对高校研发投入与区域经济增长面板数据，进行进一步的PVAR 模型GMM 估计、脉冲响应函数以及方差分解分析，讨论我国高校科技创新投入对经济增长的作用机制。

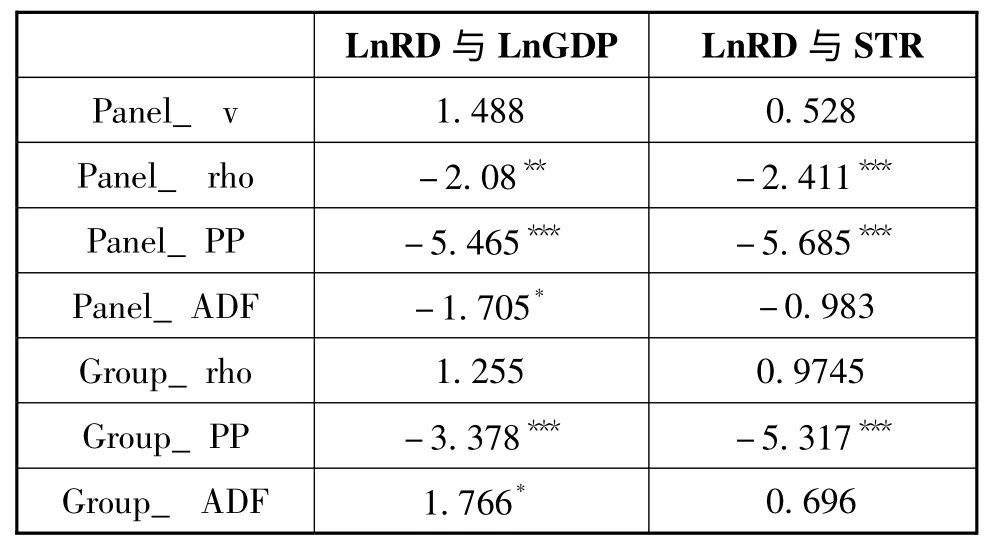
表2 面板协整检验结果

2.3 PVAR 回归分析

为了消除PVAR 模型存在的个体效应和时间效应，使变量间呈正交性，且与误差项不相关，以保证面板矩估计系数的有效性，采用横截面上的均值差分法消除面板向量自回归模型中时间效应，采用前向均值差分法消除区域固定效应。在此基础上进行1999—2011年，区域LnRD、LnGDP 之间的面板向量自回归模型的矩估计，结果见表3。

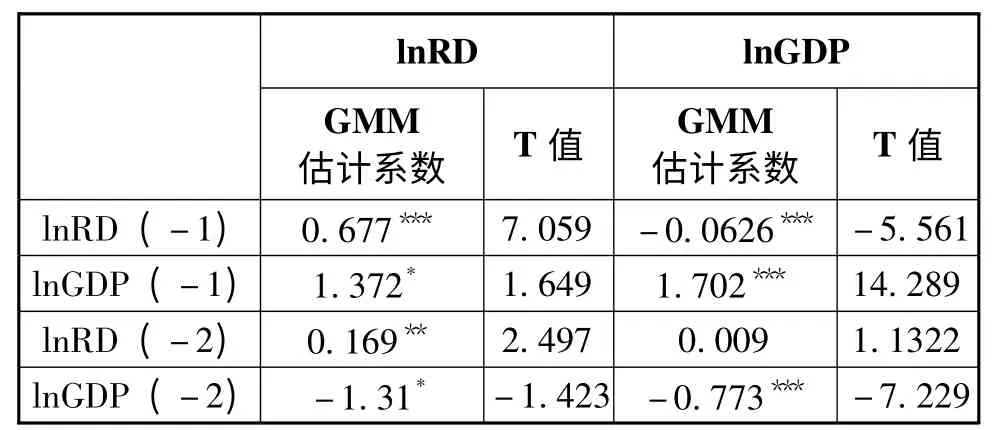
表3 基于PVAR 的区域高校R＆D 投入与经济增长GMM 估计结果

从经济增长和高校研发投入变量自身情况来看，由GMM 估计的LnRD 滞后各期的系数和对应的T 检验值可知，LnRD 的滞后一期与滞后二期变量对当期LnRD 的影响为显著正向影响，系数分别为0.677 和0.169，说明以往高校R&D 活动对当期活动存在着重要影响。LGDP 的滞后一期对其当期变量的影响也是显著正向影响，系数为1.702;滞后二期为显著负向影响，系数为-0.773。

从经济增长和高校R&D 投入之间的关系来看，LnGDP 滞后一期对当期LnRD 为正向影响，系数为1.372，滞后二期为负向影响，系数为-1.31，均通过了显著性水平为10%的检验。总体上，短期内经济增长将有效促进高校R&D 投入。LnRD 滞后一期对当期LnGDP 存在负向影响，系数为-0.0626，通过了显著性水平为1%的检验;而滞后二期对LnGDP 存在正向影响，系数为0.009，未通过显著性检验，表明我国高校R&D 投入滞后一期将对经济的增长当期存在显著的负向影响，但影响的系数很小。

2.4 脉冲响应分析

脉冲响应函数是指系统在输入为单位冲击函数时的输出响应，它刻画了给定一个随机扰动或是在随机扰动项上施加一个标准差冲击时，对系统中每一个内生变量当前和未来取值带来的动态变化轨迹。本文通过给定变量一个标准差的冲击，经过蒙特卡洛模拟500 次获得冲击反应，得到误差置信带为5%的脉冲响应函数图。图1 显示了高校R&D 投入与经济增长率之间相互影响的动态轨迹。本文中LnRD、LnGDP 等变量是通过对数变换得到的，各变量的冲击实际上是其相对变化量的冲击。为了便于表述，以下仍以高校R&D 投入冲击、经济增长冲击进行描述。

如图1 右上图所示，当给定一个标准差的经济增长的正向冲击时，高校R&D 投入对其作出了正向响应，在滞后3 期，正向响应达到最大，随后增幅逐渐减少，到滞后6 期逐渐趋向零值。反映了经济的增长促进高校R&D 投入增加动态变化，但增幅并不大。

如图1 左下图所示，当受到一个标准差的高校R&D 投入冲击时，经济增长的变化首先做出较小的正向响应，在较短的滞后期内转为负向响应，并到滞后6 期逐渐趋向稳定，经济增长响应总体上以负向响应为主，响应变化量不大，这与PVAR 模型的GMM 估计结果一致。可见目前我国高校R&D投入的增加，短期内并未带来经济的显著增长。

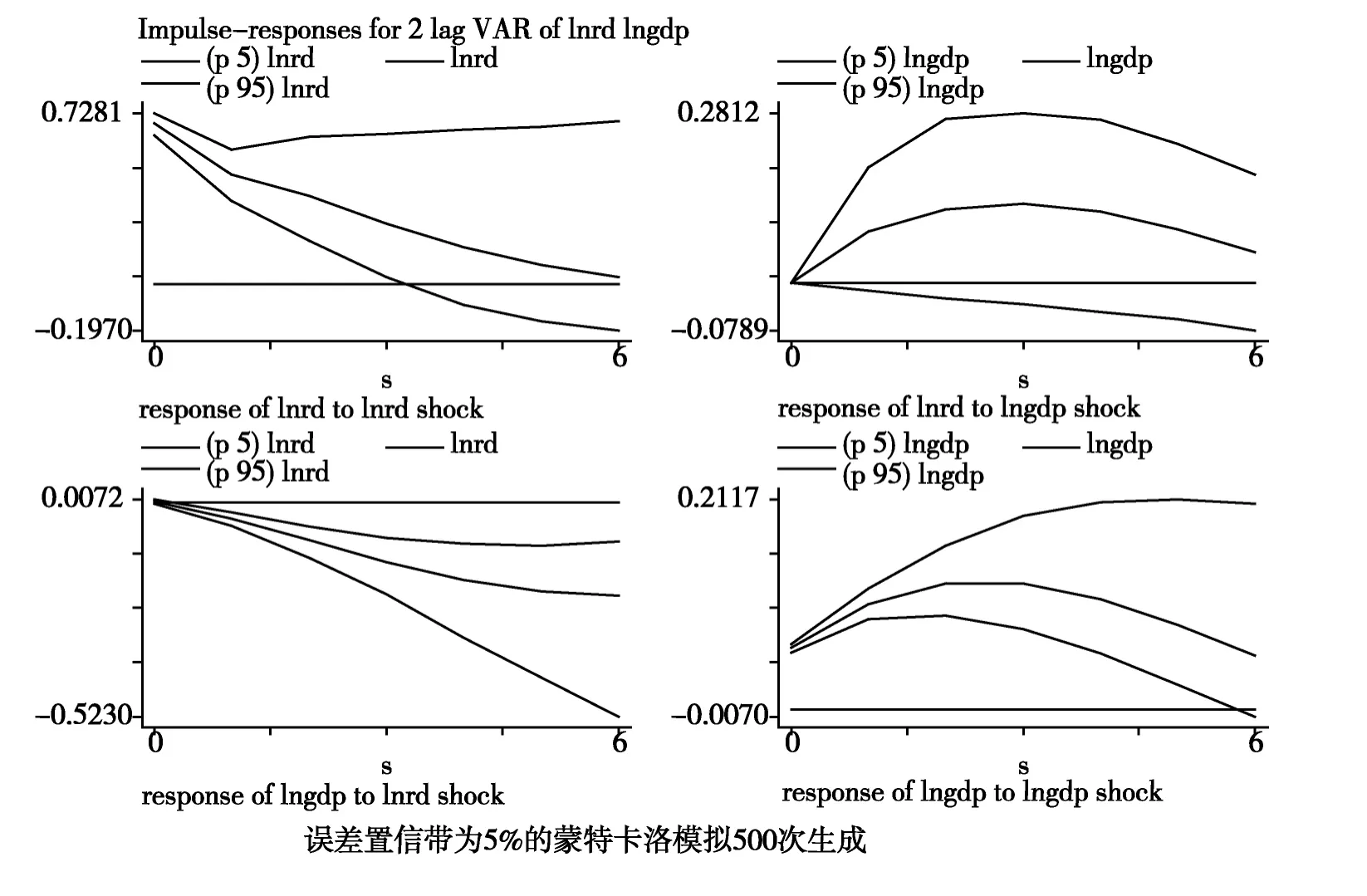
图1 基于面板VAR 模型的高校R＆D 与经济增长脉冲响应函数图

2.5 面板方差分解

本文采用方差分解计算冲击在不同时期内的相对方差贡献率，来度量冲击对内生变量的影响，并进一步考察不同冲击的相对重要程度。表4 给出了预测期为滞后10 期、20 期和30 期的方差分析结果。

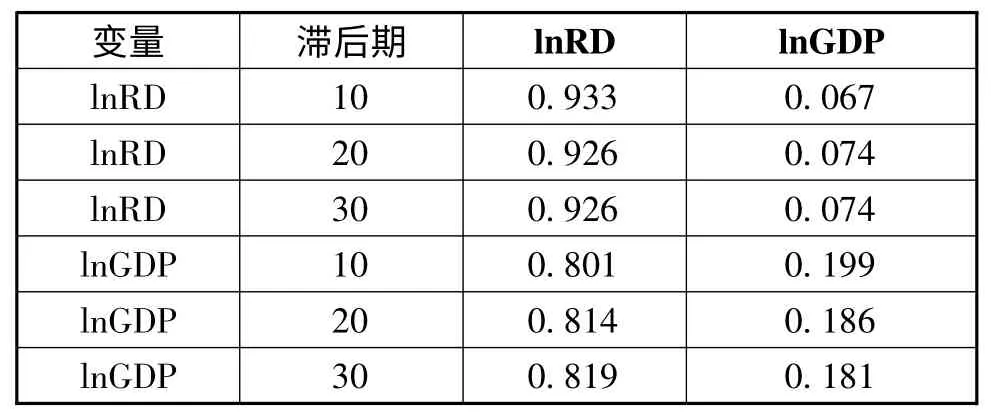
表4 基于PVAR 的区域高校R＆D 投入与经济增长关系方差分解

由表4 可知，从长远来看，高校R&D 主要受到自身的影响，滞后30 期，自身的方差贡献率基本稳定在92.6%左右。经济增长对高校R&D活动的方差贡献率相对较小，滞后30 期预测方差贡献率稳定在7.4%左右;经济增长主要受到自身与高校R&D 的影响比较大，方差贡献率均高于15%，尽管由于前面模型估计的显著性水平不高，可能会造成方差分解的偏差，但长期预测趋势与Martin、Pamela、赵文红等的研究结论基本一致。

3 结论与建议

面板协整检验表明，高校R&D 投入与产业结构之间尚未形成面板协整关系，而高校R&D 投入与经济增长之间存在长期稳定的均衡关系。因此，有必要加强高校研发活动与产业结构调整的互动关系，依托大学的科技资源优势和人才优势，为产业调整特别是主导产业调整提供人才、智力和技术支持，增强产业原始创新、集成创新和引进消化吸收能力，实现产业结构的调整和优化。同时，在产业结构的合理化、高度化和高效化过程中，从产业结构调整的实际需要出发，引导和促进高校科技创新活动的开展，提升高校科技创新的综合实力。

PVAR 模型的GMM 估计表明，滞后一期、二期GDP 显著影响当期高校R&D 的投入;高校R&D 滞后一期对当期GDP 存在显著的负向影响;脉冲响应函数分析显示，高校R&D 投入受到经济增长的正向冲击，相应地会作出动态同向响应，但响应变化量不明显。反之，经济增长负向响应高校R&D 投入的冲击，且调整量变化不大，再次验证了PVAR 分析的结论。说明短期内经济增长能够促进高校研发活动，而高校研发活动需要在人、财、物、信息、技术等多方面资源的投入，且研发活动投入产出周期较长，短期内并不能促进经济的增长，甚至带来负向影响。这与现阶段我国高校科技创新意识，高校创新与产业界、经济界的密切程度，以及创新成果的转化率普遍偏低也有着本质的联系。由此需要通过有效制度安排，完善高校科技管理体制建设，增强高校科技创新意识、提高高校研发的效率，推动高校与经济界协同合作、推进高校科技成果快速有效转移扩散，以实现高校研发活动的经济价值。

方差分解显示，从长远考察，我国经济增长对高校R&D 投入的方差贡献率在7.4%左右，经济增长受到其自身和高校R&D 的影响均较高。可知高校研发与经济增长之间存在良好的相互促进作用，且高校研发对经济增长的正向影响具有长期性和累积性，因此应立足长远，避免短期利益冲突，保持政策的持续性和稳定性，合理配置各种高校研发资源，构建研发投入与产出的良性循环。

［1］Holtz-Eakin D，Newey W，Rosen H S.Estimating vector autoregressions with panel data［J］.Econometrica:Journal of the Econometric Society，1988:1371-1395.

［2］Kao C.Spurious regression and residual-based tests for cointegration in panel data［J］.Journal of econometrics，1999，90(1):1-44.

［3］Pedroni P.Panel cointegration:Asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis［J］.Econometric theory，2004:597-625.

［4］Pedroni P.Purchasing power parity tests in cointegrated panels［J］.Review of Economics and Statistics，2001，83(4):727-731.

［5］Love I，Zicchino L.Financial development and dynamic investment behavior:Evidence from panel VAR［J］.The Quarterly Review of Economics and Finance，2006，46(2):190-210.