一个有效的稀疏轨迹数据相似性度量

肖啸骐

0 引言

随着位置感知技术[1]的发展，使得人们能够以较高的时空分辨率记录位置历史数据，对于位置历史数据的处理和分析逐渐成为新的研究热点。由于移动对象的轨迹数据的多样性和复杂性与日递增，对这些轨迹数据的挖掘和分析显得更加重要。由于移动对象的运动轨迹是不断发生变化的，轨迹点之间的时间间隔也在不断变化着，并且移动对象的轨迹的时间跨度占整个观察时间的比例很小，因此移动对象的轨迹数据在时间维度上呈现稀疏性。相似性是各项轨迹数据挖掘任务的核心，在基于位置的社交网络中需要衡量用户行为轨迹的相似性，来找出地理位置相似的用户[2]；在证券市场股票交易行为中需要衡量交易帐户的证券交易行为的相似性，来挖掘涉嫌操纵股票的交易帐户[3]；在视觉监控中需要衡量目标的运动轨迹相似性，来提供异常运动预测[4]。因此，有效的定义稀疏轨迹相似性有助于对移动对象的稀疏轨迹数据进行挖掘和分析。

欧几里德距离[5]是一种最常用的相似度表示，但它要求两轨迹的轨迹点数相等。最小外包矩形距离方法[6]是将整条轨迹划分为一些相对平滑的轨迹区间，再将每条子轨迹用其最小外包矩形表示，这样通过比较最小外包矩形序列即可度量轨迹间的相似性。它的优点是非常直观且易于理解，但是如何有效地将稀疏轨迹划分成平滑轨迹区间仍有待于研究。DTW(Dynamic time warping)是一种有效的计算不同长度的轨迹相似性方法，但它对于稀疏轨迹中的噪声数据点敏感[7]。隐马尔可夫模型(Hidden Markov Model,HMM)[8]或其他概率模型的轨迹建模方法在轨迹相似性研究中经常被使用，它的思路是先根据其他轨迹建立模型，再根据当前轨迹在模型中的生成概率来计算轨迹匹配度。概率模型在计算稀疏轨迹相似度时计算代价较大，细节区分能力不足，分析时需要额外的信息。

文献[9]中对稀疏轨迹数据进行了研究，它提出了一种基于概率的推荐模型，对大量出租车轨迹进行挖掘，分析出租车轨迹的相似性。但文献[9]中的方法在计算相似性时计算代价大，运行效率低。

编辑距离[10][11][12](Edit Distance)，又称Levenshtein距离，是指两个字符串S1和S2之间，由S1转成S2所需的最少编辑操作次数。编辑操作包括：插入、删除和替换三种操作。在基于编辑距离比较方法中，将对象轨迹视为字符串，两轨迹之间相似性就可以用编辑距离来度量。在编辑距离方法中，比较的两字符串长度可以不一致，并且字符串中可以有多个空字符(即字符串具有稀疏的特性)。 因此编辑距离适合分析移动对象的稀疏轨迹，本文也主要探讨编辑距离在移动对象的稀疏轨迹相似性上的运用。

在移动对象的稀疏轨迹中，由于噪声点的存在，使得轨迹挖掘和分析方法的精确度会受到影响。如果能找到轨迹中的关键点，在用关键点构成的轨迹来代替原轨迹，那么会在一定程度上提高轨迹挖掘和分析方法的精确度。由于移动对象的稀疏轨迹中的轨迹点分布不均匀，有些轨迹点在时间维度上比较接近，有些轨迹点在时间维度上间隔很远。如果能够有效的将时间分段，将在整个观察时间内寻找关键点的任务划分为在若干个时间子段内寻找关键点，那么也会在一定程度上提高轨迹挖掘和分析方法的效率。

1 相关工作

单纯的编辑距离直接运用到稀疏轨迹相似性分析中还有不足之处，例如ERP[13](Edit Distance with Real Penalty)适合于实数序列的方法分析，然而对于稀疏轨迹相似性分析时，还存在一些缺陷。ERP用真实值来度量距离，而不是将距离概化为0和1，所以该方法对噪声敏感。

文献[14]提出了 EDR方法(Edit Distance on Real sequence)，采用了编辑距离，通过正态化处理降低了噪声的干扰，使得度量方法更加精确。但EDR方法是针对一般的数据检索提出来的，在分析移动对象的稀疏轨迹时稍有不足。

文献[15]也提出了改进的ERP算法，采用编辑距离，定义了插入、删除和替换操作的代价函数，分析两条轨迹之间的相似性。不足之处在于分析稀疏轨迹时，它是以原始坐标数据计算的，每个坐标作为一个元素来计算编辑距离，则需要花费大量时间比较两条轨迹中所有轨迹点，导致算法效率较低。

本文针对移动对象的运动轨迹分析，考虑到运动轨迹的主要特征在于移动对象的运动方向的变化，根据编辑距离思想，提出了一种基于关键点和时间分段的稀疏轨迹相似性度量算法(Sparse Trajectory Similarity)。

2 关键点

本文提出关键点的原因是ERP和EDR方法都是以原始坐标数据计算的，每个轨迹点的坐标都作为一个元素来计算稀疏轨迹。噪声点的出现，会使得这些方法的准确率受到干扰。本文采用寻找关键点方法，找出移动对象的稀疏轨迹中的关键点，然后对关键点轨迹进行轨迹挖掘和分析，提高了准确度。

移动对象的运行轨迹是受该移动对象的意识支配的，一般在确定目的地后，行为轨迹不会发生太大的变化。通常移动对象的运动具有保持运动方向的趋势，而改变运动方向的轨迹点更有意义。如果移动对象的运行方向发生较小的变化以至于微乎其微，那么就认为移动对象继续保持着运动方向；但当移动对象的运行方向发生较大的变化，那么就认为移动对象的轨迹中运行方向发生改变。

文中给定阈值λ，当轨迹的运行方向变化超过λ时，将此时的轨迹点称为关键点，如图1所示：

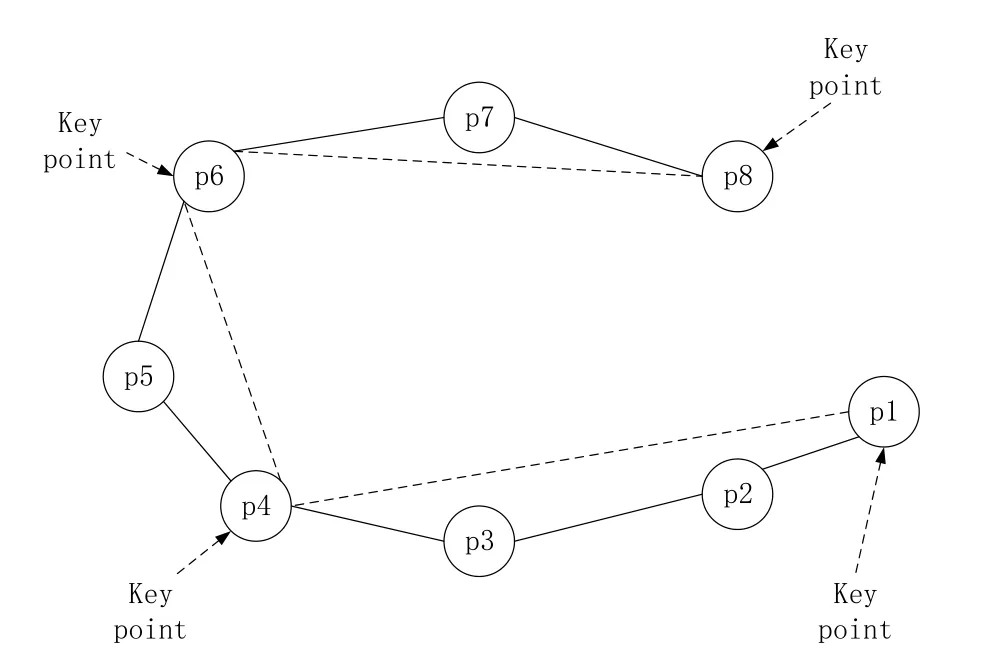
图1 示例轨迹TR

图1中的λ设为 30度，对于一条轨迹TR=p1p2p3p4p5p6p7p8，只有在p4和p6轨迹点上运行方向改变值超过了30度，因此p4和p6被视为关键点；另外p1和p8属于轨迹的开始点和结束点，也要被视为关键点。因此，图3中的关键点构成的轨迹为TRkey=p1p4p6p8。

关键点的寻找应该遵循两个原则：精确度和简明性。精确度意味着原轨迹和它的关键点轨迹之间的差异应该越小越好，体现着原轨迹运动轨迹的风貌。简明性意味着关键点数量应该越少越好，体现着轨迹挖掘和分析方法的运行效率。精确度和简明性是相对的，如果一条轨迹中所有的点都视为关键点，那么精确度达到最高，简明性达到最低，轨迹挖掘和分析方法的运行效率最低；如果只有开始点和结束点被视为关键点，那么简明性达到最高，而精确度达到最低，则很容易将两个轨迹相差很大的移动对象视为轨迹相似。因此本文寻找关键点时应该在这两个原则中达到平衡。

寻找关键点的具体规则如下：

(1)对于一条轨迹 TR=p1p2p3...pi...pn，pi(1<=i<=n)为轨迹上的点，轨迹开始点p1和结束点pn肯定为关键点。如果在轨迹pi点的运动方向变化值θi大于阈值λ，那么pi视为关键点。本文中,轨迹pi点的运动方向变化值θi的计算方法如下：

(2)如果轨迹中运动方向变化值都未超出阈值λ，根据规则(1)，仅仅会得到两个关键点：轨迹的开始点和结束点。如图2所示：

图2 示例轨迹TR

图2中阈值λ设为30度，轨迹TR= p1p2p3p4p5p6p7p8，从p2到p7中，每个点的运动方向变化值都小于阈值λ，最终只有p1和p8是关键点，这样就不能很好的反映出轨迹内部的运动变化细节，因此本文规定如果从一个关键点开始，经过η个点，仍未出现运动方向改变超出阈值λ的情况，那么将第η个点视为关键点，并依次类推。

本文将寻找关键点的算法称为KP(Key Point)算法，KP算法具体如下：

KP算法首先将轨迹开始点和结束点标为关键点(第 1行)，并且初始化关键点轨迹(第2行)，然后遍历轨迹中的轨迹点，将符合关键点条件的轨迹点标为关键点(第3-12行)，再将标记的关键点加入到关键点轨迹中(第13-17行)，最后返回关键点轨迹(第 18行)。其中 Flagi是关键标志，若 pi是关键点，则Flagi=1;否则Flagi=0。

3 时间分段

移动对象的稀疏轨迹的轨迹点在时间维度上分布不均匀，有些轨迹点之间的时间间隔很短，而有些轨迹点之间的时间间隔很长。为了提高寻找关键点的效率，如果将整个观察时间分段成若干个时间子段，并同时在这些时间子段内寻找关键点，这样会大大提高寻找关键点的效率。

当时间子段内轨迹点数较少，为了使关键点轨迹体现原轨迹的运动风貌，可以将该时间子段内的每个轨迹点都视为关键点。当时间子段内轨迹点数较多时，为了加快寻找关键点的效率，可以在该时间子段内利用 KP算法寻找关键点。因此本文给定阈值ε，当时间子段内的轨迹点大于ε时，就视为在该时间子段内利用KP算法寻找关键点；否则将该时间子段内的轨迹点都视为关键点。

接下来文中给出了时间分段的具体规则，如下：

(1)对于一条轨迹的时间序列 TR=t1t2t3...ti...tn，ti(1<=i<=n)对应轨迹上时间为ti的轨迹点，若ti与ti+1相隔时间小于阈值δ，则ti与ti+1分别对应的轨迹点属于同一段时间子段。

(2)若时间子段中的点数大于ε，则运用KP算法在该子轨迹中寻找关键点，否则将该时间子段中的点都视为关键点。

本文将针对稀疏轨迹的时间分段算法称为 TS(Time Slicing)算法，该算法具体如下：

TS算法首先初始化关键点轨迹(第1行),再遍历轨迹点，生成时间子段集合(第2-10行)，然后在时间子段中寻找关键点(第11-17行)。对于时间子段中点数大于阈值ε时，运用KP算法寻找关键点(第12-13行)；否则将该时间子段中的轨迹点都视为关键点(第 14-15)。最后返回关键点轨迹(第 18行)。

4 稀疏轨迹相似性度量及其计算算法

定义编辑距离的关键是设置合理的代价值，即编辑操作应付出相应的代价值。代价值越小，两轨迹相似性越高。在关键点和时间分段算法的基础上，本文采用编辑距离来计算插入操作的代价、替换操作的代价和删除操作的代价。

对于两条轨迹关键点构成的序列P和Q，m和n分别为序列P和Q的长度，pi为序列P的第i个元素,qj为序列Q的第j个元素，Rest(P)为P中除去当前比较字符以外的其他字符部分，Rest(Q)同理如此。计算将序列P转换为序列 Q的代价，所有操作都在序列P上进行，因为，轨迹是按时序建立的，因此，本文定义插入操作(insert)的代价为插入的坐标与当前状态前一个坐标的欧几里德距离，如公式(1)：

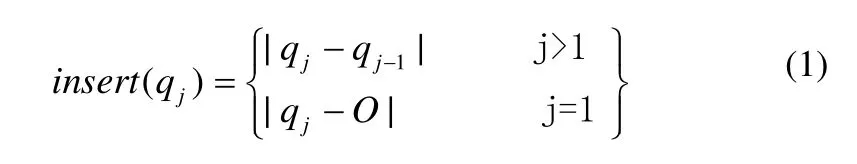
定义替换操作(substitute)的代价为替换的2个元素之间的欧几里德距离，如公式(2)：

其中，若替换的2个元素之间的欧几里德距离小于σ时，2个元素的替换操作的代价视为0，本文中σ设为单位长度的二分之一；定义删除操作(delete)的代价为删除的坐标与当前状态前一个坐标的欧几里德距离，如公式(3)：

在公式(1)、(2)和(3)中：O 代表原点坐标(0,0)；|pi-qj|为两坐标点之间的欧几里德距离。序列P和Q之间的编辑操作代价如公式(4)：

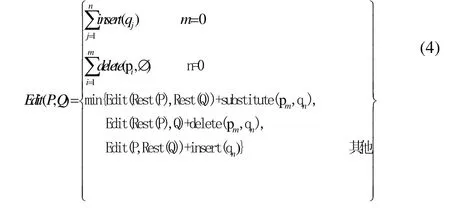
当两条稀疏轨迹之间的编辑代价越大时，表示需要更多的编辑操作，才能实现两条稀疏轨迹之间的编辑转换，则这两条稀疏轨迹间的相似性越小。当两条稀疏轨迹之间的编辑代价越小时，表示需要更少的编辑操作，就能实现两条稀疏轨迹之间的编辑转换。当编辑代价等于0时，表示不需要编辑操作，就可以实现两条稀疏轨迹之间的编辑转换，则这两条稀疏轨迹完全相同。因此以稀疏轨迹间的编辑代价为变量，稀疏轨迹之间的相似性随着编辑代价的递增而减小，随着编辑代价的递减而增大，故稀疏轨迹之间的相似性函数应满足单调递减性。因此，本文提出用于计算稀疏轨迹之间的相似性如公式(5)：

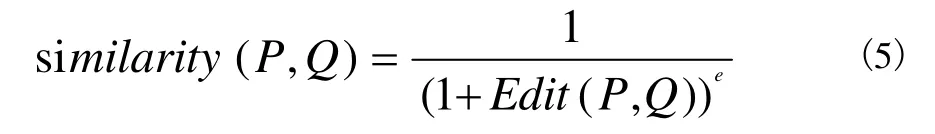
本文基于关键点和时间分段算法，提出了稀疏轨迹相似性计算算法，称为STS(Sparse Trajectory Similarity)算法，具体如下：

STS算法首先利用TS和KP算法寻找关键点(第1行)，然后根据公式(1)、(2)和(3)计算编辑代价。当第一条轨迹的关键点轨迹长度为0时，直接计算两条轨迹间的插入操作代价(第2-3行)；当第二条轨迹的关键点轨迹长度为0时，直接计算两条轨迹间的删除操作代价(第4-6行)。再通过递归函数，根据公式(4)计算得出两条轨迹间的编辑代价(第7-10行)。最后根据公式(5)，求得两条轨迹间的相似性(第11行)。

5 实验

实验平台是Windows 7，CPU 3.20GHz，内存4GB。实验采用的是旧金山的出租车 GPS移动轨迹数据[http://www.datatang.com/data/15731]，出租车数目为500辆，监控时间是30天。该数据集中的出租车轨迹稠密度差异大，是一个典型的稀疏轨迹数据集，如表1所示：

表1 出租车GPS移动轨迹数据

表1中车辆的位置信息为(北纬，西经)，例如车辆 O1在时间t1的位置为北纬37.75度，西经122.39度。

5.1 效率

实验随机抽取了3个样本数据集，包括100辆、200辆和500辆出租车在30天内的GPS移动轨迹数据。实验分别比较了STS算法与文献[15]中以原始坐标数据进行编辑距离计算的ERP算法在计算轨迹相似性的运行效率，其中阈值λ从20度依次递增1度、直到60度；阈值η从2依次递增1、直到 20；阈值ε从 2依次递增，直到 20；阈值δ从 2依次递增，直到10秒。两种算法在每种参数组合的情况下分别运行10次。两种算法在3个样本数据集上的运行结果如图3、图4、图5所示：

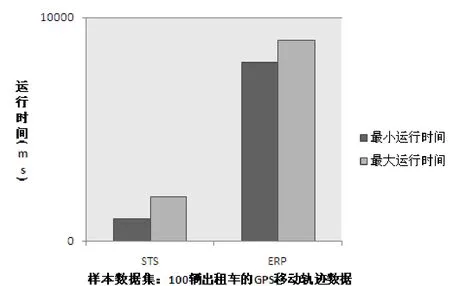
图3 STS和ERP算法在100辆出租车的GPS移动轨迹数据集上的运行

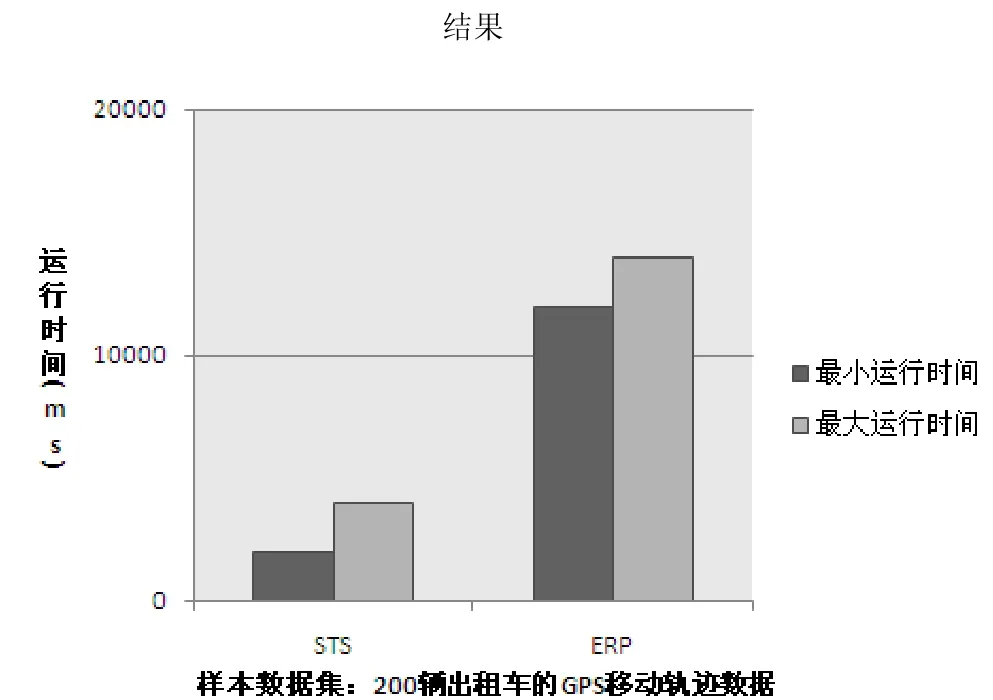
图4 STS和ERP算法在200辆出租车的GPS移动轨迹数据集上的运行结果

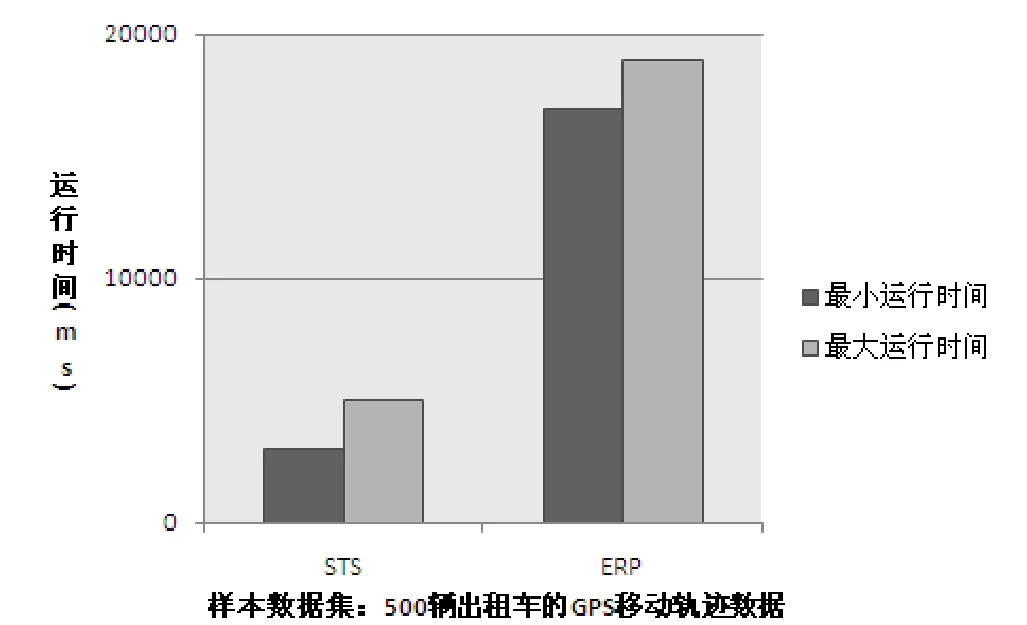
图5 STS和ERP算法在500辆出租车的GPS移动轨迹数据集上的运行结果

在图3中STS算法的最大运行时间和最小运行时间都小于ERP算法的最大运行时间和最小运行时间。在图4中STS算法的最大运行时间和最小运行时间也都小于ERP算法的最大运行时间和最小运行时间。在图5中STS算法的最大运行时间和最小运行时间也都小于ERP算法的最大运行时间和最小运行时间。

当样本中出租车辆数为100时，STS算法的最小运行时间和最大运行时间分别为1000ms和2000ms，ERP算法的最小运行时间和最大运行时间分别为8000ms和9000ms。当出租车辆数增大时，STS算法的最小运行时间和最小运行时间增幅不大,始终低于10000ms；而ERP算法运行时间增幅很大。这是因为 STS算法通过关键点的筛选，去除了不必要的计算开销，而 ERP算法始终对原始轨迹点坐标进行计算，在不必要的轨迹点上花费了大量的时间。STS算法的运行速度相较ERP算法有很大的提高。

5.2 有效性

实验分别用本文中的STS算法和文献[15]中的ERP算法对3个样本数据集进行聚类，聚类方法选用Kmeans方法，聚类结果用purity和NMI衡量。其中阈值λ从20度依次递增1度、直到60度；阈值η从2依次递增1、直到20；阈值ε从2依次递增，直到20；阈值δ从2依次递增，直到10秒。两种算法在每种参数组合的情况下分别运行10次，聚类效果如表2、表3、表4所示：

表2 STS和ERP算法在100辆出租车数据集上的聚类效果

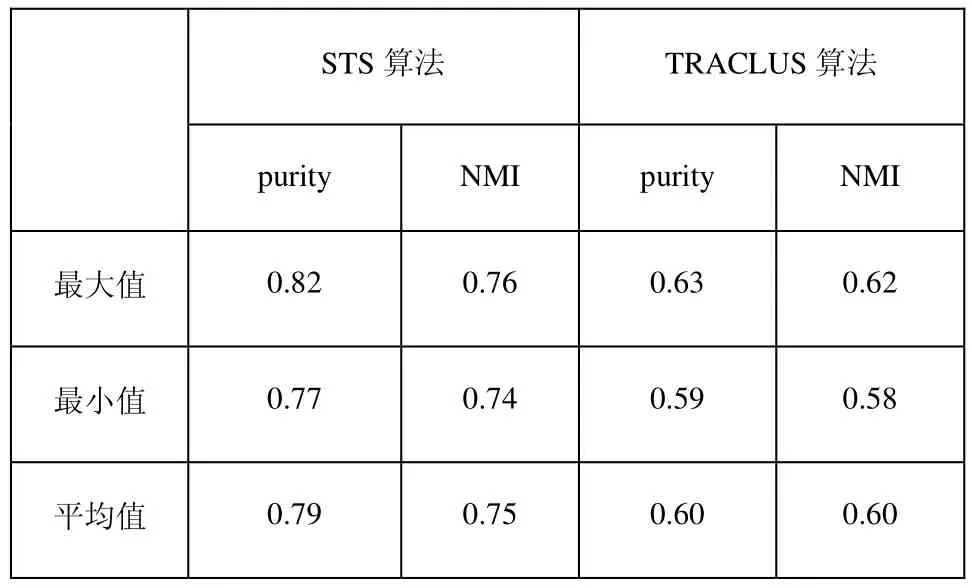
表3 STS和ERP算法在200辆出租车数据集上的聚类效果

表4 STS和ERP算法在500辆出租车数据集上的聚类效果

在对3个样本数据集进行聚类时，STS算法的聚类结果中的最大purity值和NMI值都大于ERP算法中的最大purity值和NMI值。同时STS算法的最小purity值和NMI值都大于ERP算法的最大purity值和NMI值。这是因为STS算法通过关键点的筛选，去除了噪声轨迹点的干扰，故提高了聚类准确率。ERP没有去除噪声轨迹点的干扰，所以聚类准确率低。

6 总结

本文的主要目的是研究如何用编辑距离来计算稀疏轨迹之间的相似性。本文考虑到运动轨迹的主要特征在于人或物体运动方向的变化，提出的基于关键点和时间分段的稀疏轨迹相似性计算算法，提高了传统的轨迹相似性方法分析稀疏轨迹相似性的运行效率和准确度。

[1]Jie Liu,Bodhi Priyantha,Ted Hart,Heitor S.Ramos,Antonio Alfredo Ferreira Loureiro,Qiang Wang.Energy efficient GPS sensing with cloud offloading[C].SenSys,2012:85-98.

[2]Shuo Shang,Ruogu Ding,Kai Zheng,Christian S.Jensen,Panos Kalnis,Xiaofang Zhou.Personalized trajectory matching in spatial networks[J].VLDB,2013,7.

[3]李备友.基于复杂网络的证券市场传闻扩散与羊群行为演化研究[D].南京:南京航空航天大学,2012:

[4]李策.基于轨迹分析的视觉目标异常行为检测算法研究[D].北京：中国科学院，2012:

[5]Hongbin Zhao,Han Qilong,Pan Haiwei,Yin Guisheng.Spatio-temporal similarity measure for trajectories on road networks[C].ICICSE,2009:189-193.

[6]杨泽雪,郝忠孝.空间数据库中的组障碍最近邻查询研究[J].计算机研究与发展,2013,50(11):2455-2462.

[7]Pekka Siirtola,Perttu Laurinen,Juha Roning.A Weighted Distance Measure for Calculating the Similarity of Sparsely Distributed Trajectories[C].ICMLA,2008:802-807.

[8]Alexandre Hervieu,Patrick Bouthemy,Jean-Pierre Le Cadre.A HMM-based method for recognizing dynamic video contents from trajectories[C].ICIP,2007,4:533-536.

[9]袁晶.大规模轨迹数据的检索、挖掘和应用[D].合肥：中国科技大学,2012:

[10]Horst Bunke.On a relation between graph edit distance and maximum common subgraph[J].Pattern Recognition Letters,1997,18(8):689-694.

[11]Philip Bille.A survey on tree edit distance and related problems[J].Theoretical Computer Science,2005,337(1-3):217-239.

[12]Zaiben Chen,Heng Tao Shen,Xiaofang Zhou,Yu Zheng,Xing Xie[C].SIGMOD,2010:255-266.

[13]Lei Chen,Raymond T.Ng.On the marriage of Lp-norms and edit distance[C].VLDB,2004:792-803.

[14]Chen L,Qzsu M T,Oria V.Robust and fast similaritysearch for moving object trajectories[C].ACM,2005:491-502.

[15][15]Liu Kun,Yang Jie.Trajectory distance metric based on edit distance[J].Journal of Shanghai jiaotong university,2009,43(11):1725-1729.