整体式桥台地震反应机理分析

石丽峰 ，徐 明

（1.清华大学 土木工程系，北京 100084；2.清华大学 土木工程安全与耐久教育部重点实验室，北京 100084）

1 引 言

传统的桥梁设计中桥身和桥台/桥墩之间设有支座和伸缩缝，支座和伸缩缝容易遭到腐蚀破坏和堵塞，需要经常维护及维修，不仅需要大量资金和人力，还对交通的正常运行造成影响，其弊病日益受到高度关注[1-2]。例如，根据1986年美国进行的一项调查统计，全美约57 万座桥梁中有13 万多座存在着与伸缩缝和伸缩缝装置相关的问题[3]。日本的东名高速公路，在其通车之后的8年里，平均每个伸缩缝装置的维修次数达到了1.6 次[4]。伸缩装置的破坏现象在我国也日益严重，1990年包括北京在内的13 个城市的桥梁管理部门调查了556 座桥梁，占管辖桥梁总数的22.3%，其中伸缩装置破坏的桥梁就有271 座，占被调查总数的48.7%[5]。2012年对温州市主城区96 座简支梁桥的检查结果发现，出现各种伸缩缝损坏的桥梁比例高达80%[6]。

整体式桥是一种新的桥型[7]，其桥身与桥台/桥墩刚性连接为一体，之间没有支座和伸缩缝，从根本上避免了传统桥梁中由于支座和伸缩缝而带来的维护和维修问题，能显著减少长期运营成本。由于这些优点，近20年来整体式桥在美国和欧洲得到很大重视和推广，如在美国整体式公路桥梁中得到大范围应用，最长的桥梁长度已接近400 m[8]；英国公路规范[9]建议对中短跨度桥梁应采用整体式桥型，并以此作为桥梁耐久性设计的重要措施；日本也在近年开始推广应用这种新桥型[10]。

我国幅员辽阔，有大量已建、在建和拟建的公路、铁路桥梁，据统计，2010年我国共有公路桥梁65.8 万座，其中中短跨度公路桥梁有60.8 万座。这些桥梁基本上都设有支座和伸缩缝，每年需要耗费大量资金和人力资源用于维护和维修，而整体式桥的上述优点使其值得在我国大力推广和应用。

桥梁作为交通运输的枢纽工程，若在地震中发生破坏，将会严重阻碍灾后救援和恢复重建工作的进行。然而，传统的梁式桥梁，由于桥身是简支在支座上，在地震中支座容易破坏，桥身容易发生严重错位，甚至落梁，是历次地震中道路桥梁破坏受损严重的原因之一。根据对国内外112 座梁式桥梁的震害调查，出现支座破坏的桥梁占65.2%，出现梁体移位的桥梁占 46.4%，出现落梁的桥梁占23.2%[11]。与之对比，由于整体式桥的桥身与桥台/墩刚性连接，定性地看这种桥型能够更好地抵抗地震破坏。

整体式桥的桥台按高度可分为高桥台和矮桥台两类，高桥台在欧洲常用，而矮桥台在美国常用。桥台下方的基础可为扩大基础或桩基础[12-14]。本文研究下部为扩大基础的整体式高桥台在地震作用下的反应，如图1 所示。

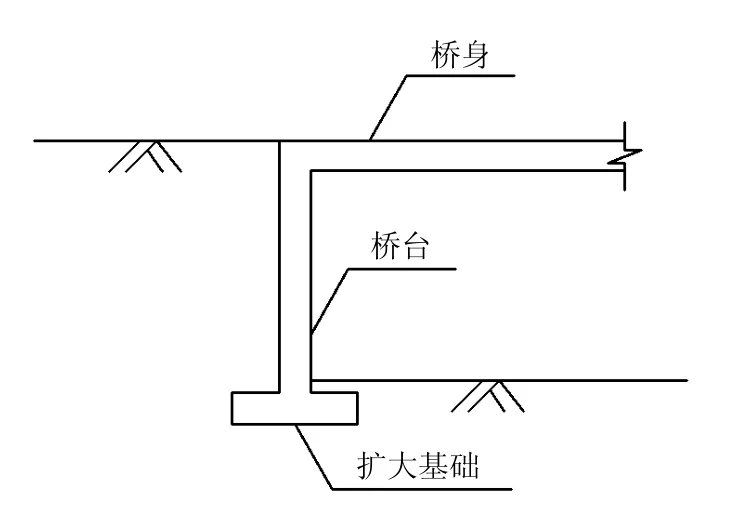
图1 整体式桥台Fig.1 Integral abutment

目前对整体式桥台的研究欧洲主要是针对季节性温度波动引起桥身长度往复伸长缩短，进而导致桥台后土压力变化[15-17]，而对整体式桥台的抗震研究主要是在美国，针对其广泛采用的矮桥台进行[18-21]，但对整体式高桥台的地震反应研究还较少。

关于地震作用下桥台后动土压力的计算方法目前都是基于日本学者物部和冈部于1923年提出的M-O 方法[22]，M-O（物部-冈部）方法是以经典的库仑土压力理论为基础的计算重力式挡墙后动土压力的拟静力方法。按照库仑土压力理论的思路，将楔形土体的重力替换为重力与地震作用力的合力，如图2 所示，根据力系平衡可以得到桥台后的动土压力的计算公式为

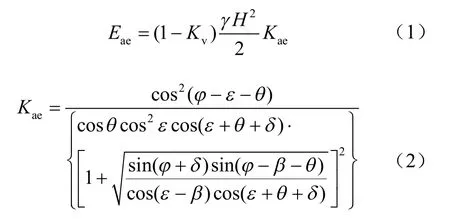
式中：Eae为动主动土压力；KH、Kv分别为水平向和竖直向的地震系数；γ为土体的重度；H为桥台高度；Kae为动主动土压力系数；φ为土的内摩擦角；ε为倾斜墙背与竖直方向的夹角；θ为地震偏角；δ为墙背摩擦角；β为倾斜土面与水平方向的夹角。

图2 物部-冈部法Fig.2 Monobe-Okabe method

在计算桥台后动土压力时，《公路桥梁抗震设计细则》[23]对M-O 方法简化后考虑总动土压力计算公式为

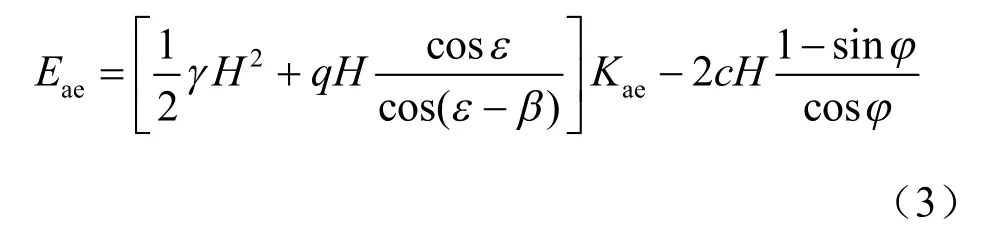
式中：q、c 考虑了滑裂楔体上均布荷载和黏聚力的影响，当q、c=0 时，公式蜕变为M-O 动主动土压力公式。桥台后地震总土压力作用位置取在距桥台底H/3 处。

《铁路工程抗震设计规范》[24]采用与式（1）、式（2）完全一致的形式。

由上述可知，目前规范中关于桥台后动土压力的计算方法是基于重力式挡墙推导的，对其是否适用于整体式桥台还存在着很大的不确定性。

本文采用二维有限差分程序FLAC，对一座典型的单跨整体式桥在地震作用下的反应进行数值模拟（基准算例），重点分析了整体式桥台后的动土压力、桥台的弯矩和变形。在此基础上，分析了地震加速度峰值、桥台高度、桥梁跨度的影响。并探讨了两种减震措施的效果，包括在桥台后增加一定厚度的隔离层以及对桥台后方采用加筋土。

2 计算模型简介

2.1 模型尺寸

本文基准算例中，原地基土厚4 m，下方为基岩。整体式桥的跨度为20 m，桥台高8 m，桥台厚为1 m，桥台下部扩大基础宽4 m。具体的模型尺寸如图3 所示。整个模型长100 m，高12 m，桥台左右两侧边界与桥台的距离，根据试算结果分别取了足够长度为40 m。

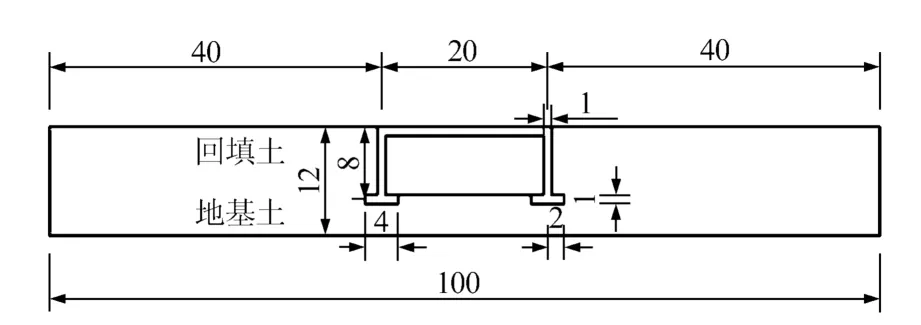
图3 整体式桥台尺寸（单位：m）Fig.3 Integral abutment dimensions(unit:m)

2.2 模型参数

地基土和回填土均为无黏性的密实砂土，土体本构采用摩尔-库仑弹塑性模型[25-27]，地基土与回填土的模型参数见表1[25]。

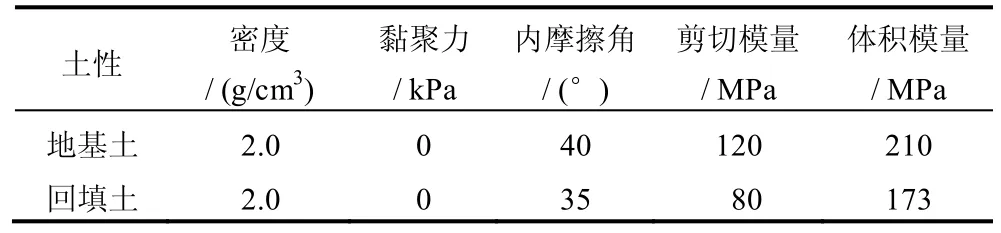
表1 土体参数Table 1 Parameters of soils

桥台和桥身采用梁单元模拟，为线弹性本构。桥台和桥身材料采用C30 混凝土，桥台模型参数见表2[28]，考虑到桥台混凝土开裂的影响，对惯性矩采用了0.4 的折减系数[25]。桥身采用整体式桥台桥梁常用的工型钢和混凝土面板的组合结构，桥身模型参数见表2。

表2 桥身模型参数Table 2 Bridge model parameters

紧靠桥台的土体采用薄层实体单元以模拟土与结构间的界面性质，厚0.1 m，摩擦角取相邻土体的1/2，其他参数同相邻土体参数。FLAC 数值分析模型如图4 所示，网格单元数为12 896 个，网格节点数为13 167 个。

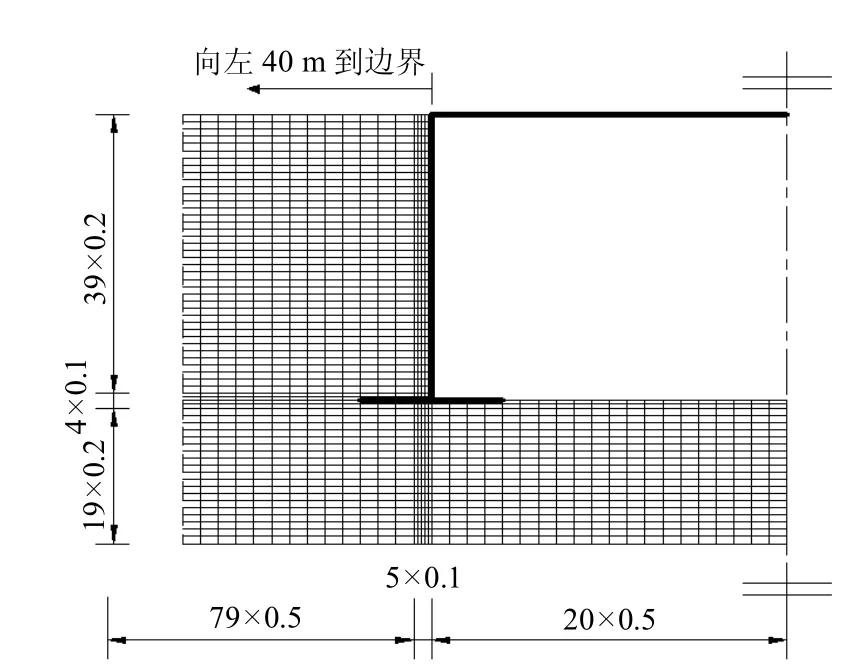
图4 FLAC 计算网格(部分)(单位:m×m)Fig.4 FLAC computing grid(part)(unit:m×m)

2.3 网格划分与边界条件

在动力分析中，由于需要考虑动力波的传播问题，所以动力问题的求解对网格尺寸有一定的要求。Kuhlemeyer 等[29]的研究表明，动力问题中网格的边长需要小于或等于输入动力荷载最高频率波长的1/8～1/10。

本文的动力荷载选用1995年日本阪神地震中的南北向加速度时程记录，以下简称Kobe 波。Kobe 波频率主要集中在10 Hz 以下，则动力分析中允许的最大网格尺寸为2 m。本文中土体网格尺寸取0.5 m（宽）×0.2 m（高），其中土体与桥台之间的薄层单元厚度（水平）方向取为0.1 m，（见图4）。

静力分析时，底边界为固定支座，左右竖直边界采用滑移支座约束水平位移。动力分析时，将静力分析得到的应力状态保留，将速度场、位移场置0，在左右竖直边界施加自由场边界，模型底部输入地震波。

2.4 阻尼确定与地震波的输入

本文采用瑞利阻尼。瑞利阻尼的确定需要2 个参数：最小临界阻尼比和最小中心频率。对于岩土材料，临界阻尼比的范围一般是2%～5%，本文阻尼比根据经验取3%[25]。中心频率取桥台的自振频率为4.7 Hz。

根据建筑抗震设计规范，Kobe 波取8 度地震的峰值加速度为0.2 g，地震加速度时程如图5 所示。

图5 Kobe 波Fig.5 Kobe wave

2.5 数值模拟过程

对于悬臂式桥台在地震作用下的动力响应模拟过程分4 个步骤：

①建立地基土网格模型，模型底部施加竖向和水平向约束，两侧施加水平向约束，进行重力场平衡计算。

②建立整体式桥模型，进行重力场平衡。

③分层回填桥台后的填土，每次回填0.8 m，分10 次完成回填，每次回填均进行重力场平衡计算。

④模型两侧施加自由场边界，模型位移场清0，设置模型阻尼，底部施加水平向的加速度地震波，进行地震反应计算分析。

3 计算结果分析

3.1 基准算例

图3 中的模型为基准算例，考虑到左右桥台动力响应规律上的相似性，本文中重点分析左桥台的反应。工程设计规范中依据的M-O 方法是基于桥台最大土压力时的桥台反应，本文取总土压力最大时刻为桥台动力响应最大时刻，分析此时桥台和土压力的响应。

从图6(a)中可以看出，桥台后回填施工结束时，整体式桥台上部由于受到桥身的支撑作用，土压力略大于主动土压力；中部由于回填过程中桥台发生了水平变形，土压力接近主动压力；而桥台下部受到了扩大基础的限制，土压力大于主动土压力。

动力响应最大时刻土压力较地震前增加了很多，特别是桥台上半部，由于桥身质量导致的水平惯性力的作用，桥台后土压力增加更加明显，形状也与采用三角形动土压力分布假设的M-O 方法有较大差别，可见用M-O 方法计算整体式桥台后动土压力是不安全的。

另外，地震开始前，由于桥身自重的影响，桥台顶部存在着相当大的负弯矩，见图6(b)。由于动力响应最大时刻桥台后土压力增加明显，桥台底部和中部弯矩也有较大增幅。

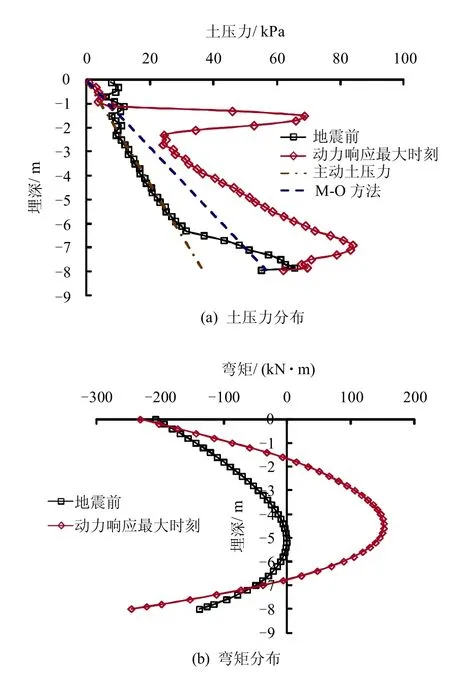
图6 整体式桥台土压力和弯矩分布Fig.6 Earth pressure and bending moment of integral abutment

3.2 地震加速度峰值的影响

在基准算例的基础上，本文研究了不同加速度峰值的影响。从图7(a)中可以看出，在地震加速度峰值为0.1g和0.2g 时，桥台弯矩最大值位于桥台底部；当地震加速度峰值为0.3g、0.4g、0.5g 时，桥台弯矩最大值位于桥台中部附近。这种现象机理可以从图7(b)中看出，在动力响应最大时刻，当地震加速度峰值为0.1g、0.2g 时，桥台顶部和底部的水平位移量均较小，底部位移量更小，底部类似固定支座形式，所以桥台底部为负弯矩。当地震加速度峰值达到时0.3g 以上时，桥台底部由于薄层单元屈服而导致较大的水平位移，此时底部由接近于固定支座形式转变为接近于滑动支座形式，桥台底部弯矩变为正弯矩，而桥台中部的正弯矩也有大幅度的增加。由图7(c)可以看出，当加速度峰值增加时，桥台和土体的相互作用增加，同时桥身惯性力也增加，导致桥台上部的土压力增加明显；并且加速度峰值越高，上部土压力增加的幅值及深度越明显；由于在加速度峰值增加时，桥台底部的基础已开始滑动，所以桥台下部2 m 深度范围内土压力增加不太明显，甚至在强震（0.5g）作用下有所减小。

图7 不同加速度峰值动力响应最大时刻弯矩、水平位移、土压力分布Fig.7 Abutment bending moment,horizontal displacement and earth pressure at the maximum dynamic response time for different peak accelerations

为验证规范中动土压力计算方法的适用性，本文对相同高度（8 m）悬臂式桥台的地震反应进行了一组对比计算[30]，如图8(a)所示。从图中可以看出，用M-O 方法计算出的悬臂式桥台后总土压力在0.1g～0.3g 时偏小，但在0.4g 以上时给出偏大（偏保守）的结果，并且臂式桥台后总土压力的合力作用点在1/3 桥台高度处，与M-O 方法中土压力的三角形分布假设比较接近。

与之对比，整体式桥台在不同加速度峰值下总土压力值均大于M-O 方法的计算结果，最大时相差近一倍，可见M-O 方法会严重低估地震作用下整体式桥台后的动土压力，造成不安全的设计。由图8(b)可以看出，动力响应最大时刻整体式桥台后总土压力的合力作用点位置，会随着加速度峰值的增加而上升，加速度峰值为0.1g 时，总土压力作用位置在距桥台底部约1/3 处；加速度峰值提高到0.5g 时，总土压力作用位置上升到距桥台底部约1/2 处。合力作用点越接近桥台中部，对桥台弯矩的影响越大，可见M-O 方法也不能正确估计出整体式桥台后总土压力的合力作用点位置。

图8 动力响应最大时刻总土压力大小、位置与M-O 方法对比Fig.8 The magnitude and position of total earth pressure compared with the M-O method at the maximum dynamic response time

3.3 桥台高度的影响

在基准算例的基础上，分别计算桥台高度不同（6、8、10 m）的地震反应。动力响应最大时刻土压力分布如图9(a)所示。从图中可以看出，桥台高度增加时，桥台后土压力增加。从图9(b)中可以看出，当桥台高度达到一定值（10 m）时，桥台的主要变形由整体倾斜变为弯曲；同时，由于土压力增大，扩大基础底部界面单元发生屈服而发生较大位移。此时桥台的最大弯矩由桥台底部转移到中部，并且此时该最大弯矩会随桥台高度的增加而迅速增大，对桥台抗震不利，见图9(c)。

图9 不同桥台高度动力响应最大时刻桥台土压力、水平位移和弯矩分布Fig.9 Earth pressure,abutment horizontal displacement and abutment bending moment at the maximum dynamic response time for different abutment heights

3.4 桥梁跨度的影响

分别取10、20、30 m 跨度的桥台进行动力响应计算分析，分别计算动力响应最大时刻的桥台后土压力和桥台弯矩，如图10 所示。从图10(a)可以看出，当桥梁跨度增加时，由于桥身质量和惯性力增加，桥台顶部土和结构相互作用增强，使得桥台上部土压力随桥梁跨度的增加而增大，并且土压力增加的深度也相应增加。从图10(b)可以看出，桥台顶部的负弯矩随着桥梁跨度的增加而显著增大，30 m 跨度的桥台顶部负弯矩最大，桥台底部弯矩变化不明显。过大的桥梁跨度会导致桥台后土压力和桥台弯矩的增大，对桥台抗震不利。

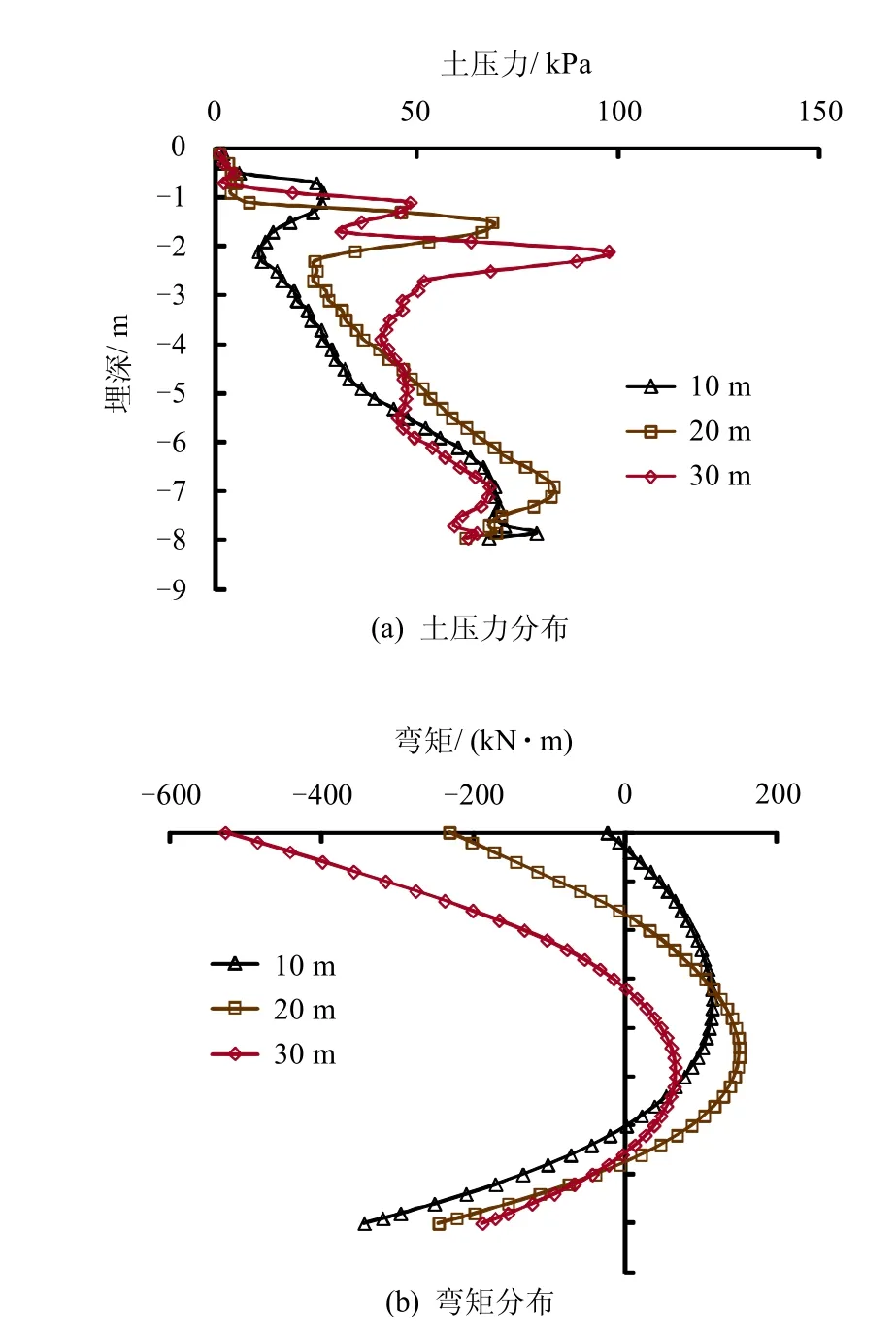
图10 不同跨度动力响应最大时刻桥台土压力和弯矩分布Fig.10 Earth pressure and abutment bending moment at the maximum dynamic response time for different bridge spans

3.5 桥台后隔离层的影响

目前有两种方法被认为可以用于减小整体式桥台后土压力，一种是在桥台后增加泡沫材料隔离层；另一种是对桥台后的填土进行加筋处理。本节主要探讨在桥台后增加泡沫材料（泡沫聚苯乙烯）的效果。在紧靠桥台后的20 cm 内增加泡沫材料，该泡沫材料采用线弹性实体单元模拟，参数见表3[31]。

表3 泡沫材料参数Table 3 Parameters of flexible layer

动力响应最大时刻时的桥台后土压力分布如图11(a)所示。

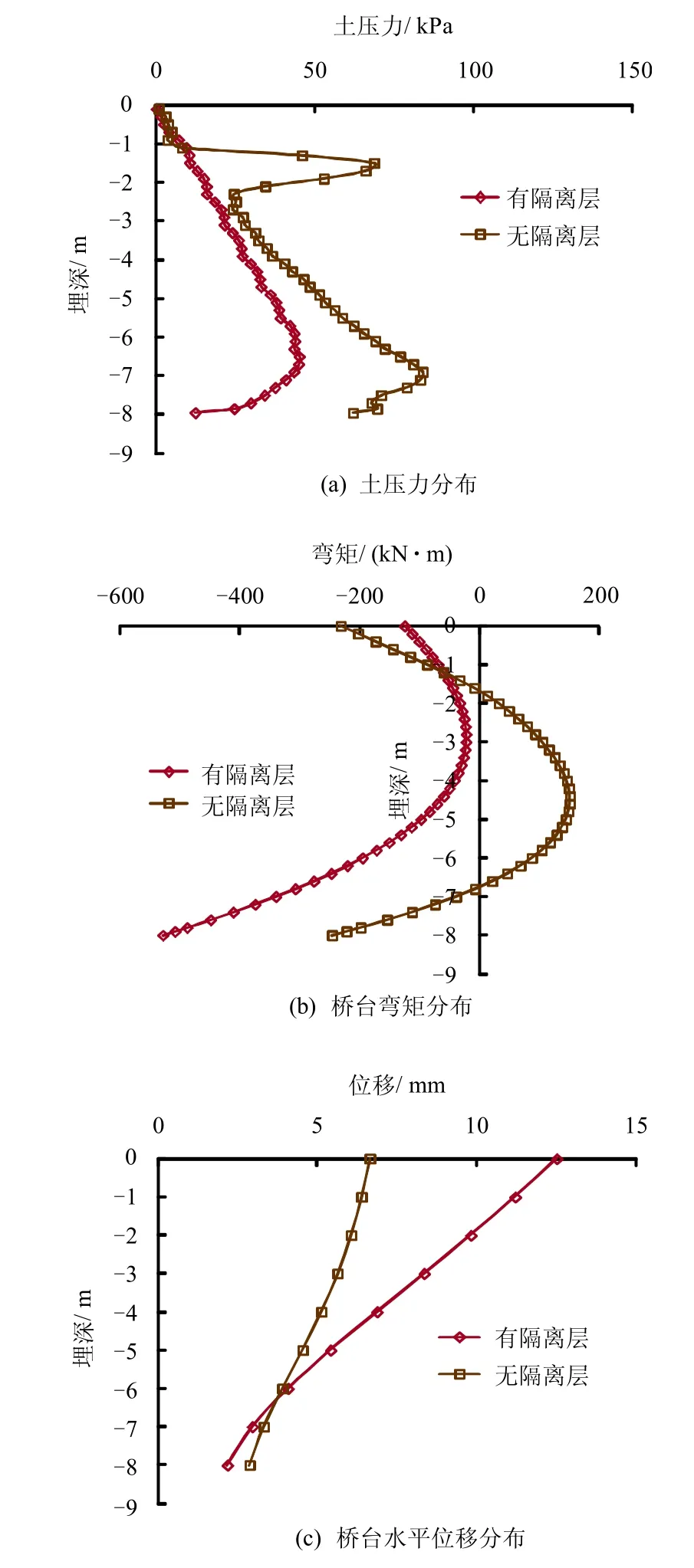
图11 有无隔离层动力响应最大时刻桥台土压力、弯矩、水平位移分布Fig.11 Earth pressure,abutment bending moment and abutment horizontal displacement at the maximum dynamic response time with and without flexible layer

从图11 中可以看出，增加该隔离层较没有隔离层的桥台后的土压力明显减小，但从图11(b)可见，增加隔离层后桥台上最大弯矩（为桥台底部负弯矩）反而增大，这是由于当桥台后增加隔离层后，由于隔离层模量很小，对桥台的水平约束作用降低，在地震过程中桥台的变形加大。从图11(c)可知，增加隔离层后的桥台在动力响应最大时刻的变形要大了很多，特别是桥台上部，该位置直接受桥身惯性力作用。因此，在地震作用下增加隔离层会降低土对桥台的侧向约束作用，导致最大弯矩增加，在抗震设计中不建议采用隔离层。

3.6 桥台后加筋的影响

在桥台背后填土中采用加筋材料土工格栅，长度为6 m，高度方向间隔为0.4 m，加筋材料用线弹性模型梁单元模拟，弹性模量为1 GPa，截面积为0.02 m2，惯性矩为6.67×10-7m4。数值模型如图12所示。

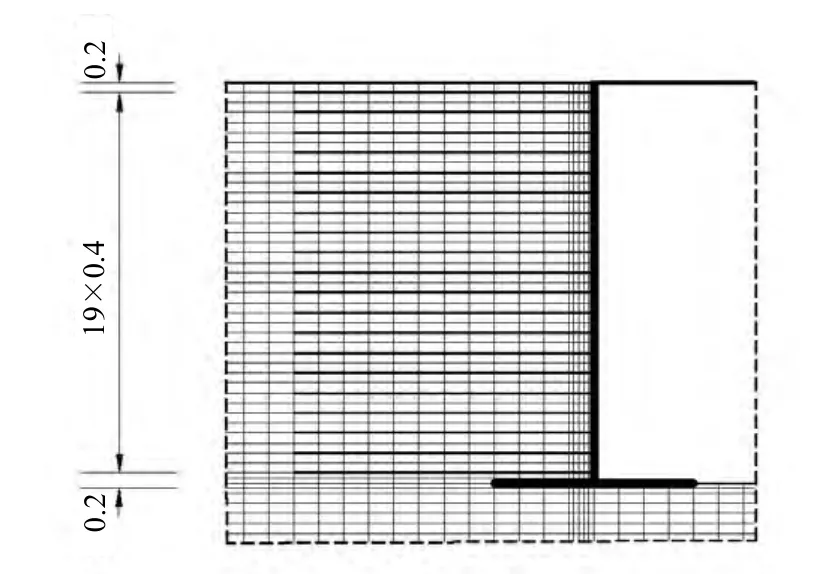
图12 整体式桥台加筋后数值模型（部分）（单位：m）Fig.12 Numerical model of abutment and soil reinforcement(part)(unit:m)

整体式桥台背后增加加筋材料后，在地震过程中，由于土工格栅能够提供水平拉力，桥台动力响应最大时刻的弯矩、水平位移均明显降低，如图13所示。对于整体式桥台，在桥台背后增加土工格栅加筋材料会减小桥台的动力反应，在一定程度上可以提高桥台的抗震性能。

图13 有无加筋动力响应最大时刻桥台弯矩和水平位移分布Fig.13 Abutment bending moment and horizontal displacement at the maximum dynamic response time with and without soil reinforcement

4 结 论

（1）目前桥台抗震规范采用的M-O 方法不能合理描述整体式桥台后动土压力的大小和分布。在地震作用下，整体式桥台后最大土压力要比M-O 方法的预测结果大得多，同时整体式桥台后总土压力的作用点位置会随着地震加速度峰值的增加而上升。

（2）地震加速度峰值增加导致土压力增加，使桥台底部基础发生滑移，从而导致桥台弯矩最大值从桥台底部上移到桥台中部附近。

（3）增加桥台高度时，桥台变形由整体倾斜变为弯曲，并且容易造成桥台底部基础的滑移，使得桥台中部附近的最大弯矩大幅增加。增加桥梁跨度时，由于桥身质量和惯性力增加，会导致桥台上部的土压力和负弯矩增幅较大。

（4）桥台后增加低模量的泡沫材料隔离层虽然会减小在地震作用下的动土压力，但同时也会减小桥台后土体对桥台侧向变形的约束作用，导致在动力响应最大时刻桥台的变形和弯矩都有较大增加，对桥台抗震是不利的，在整体式桥台抗震设计时不建议使用隔离层。

（5）桥台后采用加筋土时，由于加筋能够提供水平拉力，可以显著减小桥台在动力响应最大时刻的最大弯矩和水平位移，建议抗震设计时在整体式桥台后采用加筋土来提高桥台的抗震性能。

[1]刘丽平.化学融雪与大桥结构耐久性[J].中国市政工程,2008,132(2):22-23.LIU Li-ping.Chemical snowmelt and the durability of bridge structure[J].China Municipal Engineering,2008,132(2):22-23.

[2]WALLBANK J.The performance of concrete in bridges:A survey of 200 highway bridges[M].London:HMSO,1989.

[3]WOLDE-TINSAE A M,KLINGER J E.Integral abutment bridge design and construction[M].U.S.A:University of Maryland,1987.

[4]小烟阳康,藤原博,王剑波.桥梁伸缩装置的研究:关于埋设式伸缩缝的应用[J].国外桥梁,1990,28(4):57-65.WANG Jian-bo.Research of bridge expansion:applications on embedded type expansion joints[J].Foreign Bridges,1990,28(4):57-65.

[5]李扬海,程潮洋,鲍卫刚.公路桥梁伸缩装置[M].人民交通出版社,1997.

[6]胡植,谢尚利.城市简支梁桥病害统计与成因分析[J].城市道桥与防洪,2012,29(4):115-116.HU Zhi,XIE Shang-li.Disease statistics and causes of city charpy bridge[J].Urban Roads Bridges &Flood Control,2012,29(4):115-116.

[7]HAMBLY E C.Integral bridges[J].Proceedings of the ICE-Transport,1997,123(1):30-38.

[8]BURKE JR M P.Integral and semi-integral bridges[M].Oxford:Wiley-Blackwell,2009.

[9]Her Majesty’s Stationery Office(HMSO).BD 57/95 Design for durability[S].London:HMSO,1995.

[10]TATSUOKA F,HIRAKAWA D,NOJIRI M,et al.A new type of integral bridge comprising geosyntheticreinforced soil walls[J].Geosynthetics International,2009,16(4):301-326.

[11]王再荣,郭恩栋,赵钊,等.梁式桥震害及其影响因素分析[J].灾害学,2010,25(3):37-41.WANG Zai-rong,GUO En-dong,ZHAO Zhao,et al.Beam bridge damage and its influencing factors[J].Journal of Catastrophology,2010,25(3):37-41.

[12]彭大文,林志平,洪锦祥.无伸缩缝桥梁的研究与实践[J].公路,2006,51(8):53-62.PENG Da-wen,LIN Zhi-ping,HONG Jin-xiang.Research and practice of jointless bridges[J].Highway,2006,51(8):53-62.

[13]洪锦祥.整体式桥台桥梁的简化计算模型与受力性能研究[博士学位论文D].福州:福州大学,2005.

[14]徐明.整体式桥台后粗粒土填料力学特性的试验研究[J].土木工程学报,2010,57(5):136-141.XU Ming.Test research of mechanical properties of coarse-grained soil filler behind integral abutment[J].China Civil Engineering Journal,2010,57(5):136-141.

[15]XU M,CLAYTON C R,BLOODWORTH A G.The earth pressure behind full-height frame integral abutments supporting granular fill[J].Canadian Geotechnical Journal,2007,44(3):284-298.

[16]WRIGLEY B.Integral bridges:A fundamental approach to the time-temperature loading problem[J].Concrete,2000,34(8):39-39.

[17]COSGROVE E.Cyclic loading of sand behind integral bridge abutments[D].ProQuest:UMI Dissertations Publishing,2001.

[18]WILSON J C.Stiffness of non-skew monolithic bridge abutments for seismic analysis[J].Earthquake Engineering &Structural Dynamics,1988,16(6):867-883.

[19]KARANTZIKIS M,SPYRAKOS C C.Seismic analysis of bridges including soil——Abutment interaction[C]//Proc.12th World Conference on Earthquake Engineering.Auckland,New Zealand:[s.n.],2000.

[20]MYLONAKIS G,PAPASTAMATIOU D,PSYCHARIS J,et al.Simplified modeling of bridge response on soft soil to nonuniform seismic excitation[J].Journal of Bridge Engineering,2001,6(6):587-597.

[21]GOEL R K.Earthquake characteristics of bridges with integral abutments[J].Journal of Structural Engineering,1997,123(11):1435-1443.

[22]王洪瑾,陈仲颐,周景星.土力学[M].北京:清华大学出版社,1994.

[23]重庆交通科研设计院.JTG/T B02-01-2008 公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.

[24]铁道部.GB 50111-2006 铁路工程抗震设计规范[S].北京:中国计划出版社,2006.

[25]GREEN R A,OLGUN C G,CAMERON W I.Response and modeling of cantilever retaining walls subjected to seismic motions[J].Computer-Aided Civil and Infrastructure Engineering,2008,23(4):309-322.

[26]CHEN Y C.Seismic bearing capcity of shallow and deep strip foundations[D].London:Imperial College,1997.

[27]POTTS V.Finite element analyses of the seismic loading of deep foundations[D].London:Imperial College,2000.

[28]DICLELI M,ERHAN S.Effect of soil and substructure properties on live-load distribution in integral abutment bridges[J].Journal of Bridge Engineering,2008,13(5):527-539.

[29]FRANCISCO M,FERNANDO R.Spurious reflections and accuracy of finite element models for unbounded wave propagation problems:The one-dimensional case[J].Engineering Computations,1987,4(2):139-148.

[30]石丽峰.地震作用下整体式桥台的动力响应数值模拟与试验研究[D].北京:清华大学,2013.

[31]彭大文,陈晓冬.整体式桥台桥梁台后土压力的季节性变化研究[J].岩土工程学报,2003,25(2):135-139.PENG Da-wen,CHEN Xiao-dong.Research of pressure behind integral abutment changing with season[J].Chinese Journal of Geotechnical Engineering,2003,25(2):135-139.