含双裂隙岩石裂纹演化机理的离散元数值分析

蒋明镜 ，陈 贺，张 宁 ，房 锐

（1.同济大学 土木工程学院地下建筑与工程系，上海 200092；2.同济大学 土木工程防灾国家重点实验室，上海 200092；3.同济大学 岩土及地下工程教育部重点实验室，上海 200092；4.陆地交通气象灾害防治技术国家工程试验室，昆明 650011）

1 引 言

岩体是含有大量裂隙、极不均匀、各向异性、非连续、非弹性的损伤材料，其力学特性极其复杂，关于含裂隙岩体的变形、强度及其裂纹扩展方面的研究一直是岩土工程界中的前沿研究方向[1]。岩体力学试验是研究岩体破坏特性最有效和最直接的方法，朱维申等[2]采用类岩石材料，研究了雁形双裂隙的起裂、扩展和岩桥的贯穿机制。Bobet 等[3]采用石膏试样，系统地研究了含2 条不同分布形式裂隙试样的破坏模式。Shen 等[4]采用石膏试样，研究了闭合型和张开型的双裂隙对试样破坏模式的影响。李银平等[5]进行了含预制双裂隙试样的单轴压缩试验，观测了加载过程中的翼裂纹和次生裂纹的扩展过程和试样的破坏模式。杨圣奇等[6]对含预置平行双裂隙的大理岩石试样进行了单轴压缩试验，给出了预制裂隙倾角和岩桥长度对裂纹起裂和贯通模式的影响，并提出了裂纹扩展模式的8 种类型。Lee等[7]分别以有机玻璃、石膏和花岗岩石作为试验材料，对含有不同角度的预制雁形双裂隙试样进行了单轴压缩试验，研究了裂纹的起裂和岩桥贯通破坏模式。然而，由于现有观测仪器的限制，岩体力学试验更多的集中于对岩石试样破坏模式上的描述和分析，对岩石破坏机理的研究较少，另外，岩石试验一般具有成本大、耗时、不可重复等诸多不利因素[8]。因此，很多学者采用数值模拟来研究预制双裂隙试样的裂纹扩展与贯通机理。Reyes 等[9]较早地运用有限单元法对含2 条预制裂隙岩体试样的裂纹起裂、扩展以及贯通模式进行了研究。唐春安等[10-11]基于有限元的思想，考虑到岩石的各向异性、非均质和非连续性，开发了岩石破裂过程分析系统RFPA2D，并用于研究岩石的破裂特性和裂纹的扩展演化机理。Wong 等[12]利用RFPA2D，系统地研究了预制裂隙的长度和倾角对裂纹扩展模式的影响。Bobet 等[13]将断裂力学中的裂纹起裂应力准则导入了直接边界元法，研究了预制双裂隙试样的裂纹起裂机理。Jiao 等[14]提出了非连续变形接触本构模型，并用于模拟节理岩体的破裂过程。岩石裂纹扩展与贯通机理方面的数值方法还有边界单元法[15]、流行元法[16]等。然而，由于岩体本身的特性，若采用连续介质力学的数值分析方法对其进行破裂分析存在着一些不足之处。

近年来，由于离散单元法不涉及复杂的宏观本构模型的建立和选取等问题，且能够从宏微观层面上对数值模拟结果进行分析，因此，该方法在岩石的数值模拟中也得到迅速的推广和应用。Potyondy等[17-18]采用BPM 胶结模型，模拟了Lac du Bonnet花岗岩的力学特性，充分地说明了离散单元法能够很好地模拟岩石的力学特性。Cho 等[19]和Christian等[20]提出了用于模拟岩石的力学模型，模拟了岩石的破坏特性和裂纹扩展规律。蒋明镜等[21-23]基于室内胶结铝棒的接触试验，初步地探索了岩石微观胶结模型。通过模拟一系列岩石室内试验，表明了该方法的合理性和可行性。Wong 等[24]采用离散单元法中自带的胶结模型，研究了预制裂隙尺寸对裂纹扩展路径和试样强度特性的影响。关于采用离散单元法分析岩石的基本力学特性和破裂机理方面的研究，前人做出了较大的贡献，并取得了很多可喜的成果。

近期笔者从试验资料出发，建立了一个合理的岩石微观胶结模型，并进行了充分的验证，分析了水泥胶结颗粒的室内接触试验，提取了无胶结厚度含抗转动能力的岩石微观力学模型并导入了离散单元法商业软件，采用该方法模拟了一系列岩石室内试验与含双裂隙岩石试样的裂纹扩展规律，与室内实测数据进行了对比。本文在此基础之上，进一步模拟了含不同预制倾角的双裂隙岩石试样在单轴压缩作用下的裂纹扩展规律，揭示了裂纹扩展的宏微观机理，给出了预制裂隙岩石的强度随预制倾角的变化规律，并将试样的破坏模式和强度特性与室内试验实测结果进行了比较分析。

2 微观胶结力学模型

2.1 模型强度准则简介

矿物晶粒、晶粒之间的接触和微观缺陷是大部分岩石的主要组成成分[25]，矿物晶粒接触的力学行为对岩石力学特性具有较大的影响，因此，胶结接触模型的选取是采用离散单元法模拟岩石的关键。为此，蒋明镜等[26-31]采用类岩石材料水泥将2 根铝棒胶结在一起，系统地研究胶结铝棒的力学特性。具体的试验过程和结论见文献[26-31]。

经处理室内胶结铝棒试验获得的数据，分析得到如图1 所示强度包线，峰值剪切荷载和峰值扭转荷载先随法向力的增加而增加，而后又随法向力的增加而减小。通过拟合得到峰值强度包线表达式为

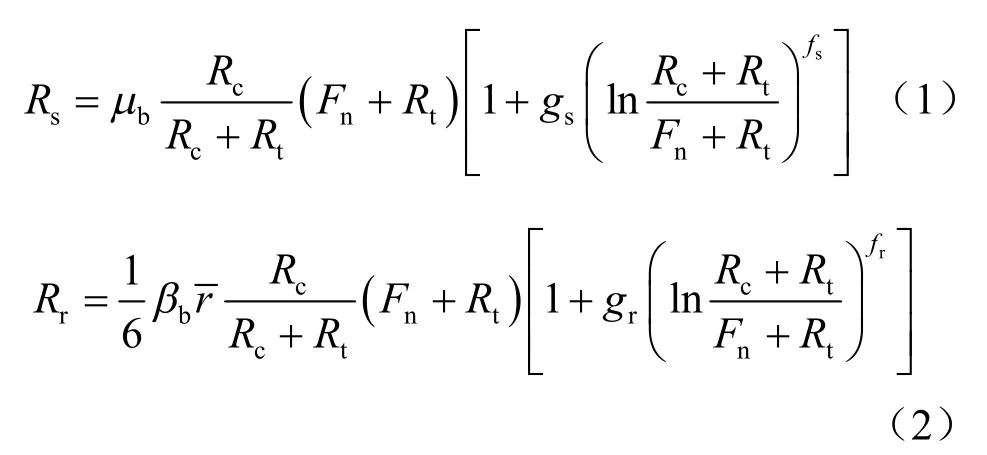
残余强度包线为

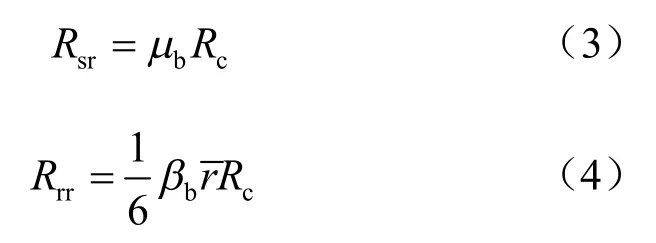
式中：Rc为峰值压缩荷载；Rt为峰值拉伸荷载；为平均粒径；μb为胶结的摩擦系数；βb为胶结的抗转动系数；fs、fr、gs、gr为形状参数，分别为0.986、0.761、2.150和3.055。

图1 有厚度(0.6 mm)的胶结颗粒的强度包线Fig.1 Strength envelope of the cemented particles with 0.6 mm bond thickness

水泥的流动性较差给无厚度水泥胶结试样的制备带来了较大的困难，即使制备出试样，试验结果也不理想，无法完成无厚度水泥胶结室内微观接触试验，因此，基于有厚度水泥胶结颗粒的试验结果，通过理论分析推导出无厚度胶结颗粒的强度包线。限于篇幅，推导过程会在另文做详细介绍，这里只给出相应的结果。图2为无厚度的胶结颗粒的强度包线，相应的峰值强度包线为

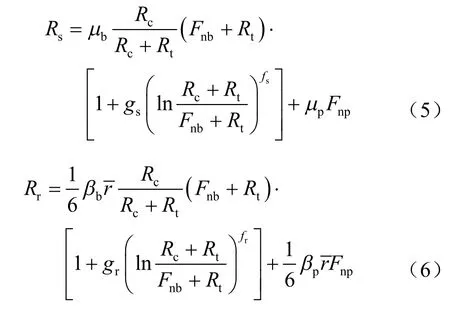
残余强度包线：

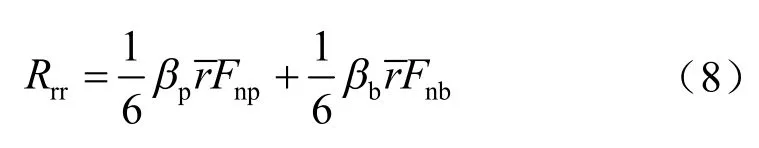
式中：μp为颗粒的摩擦系数；βp为颗粒抗转动系数。

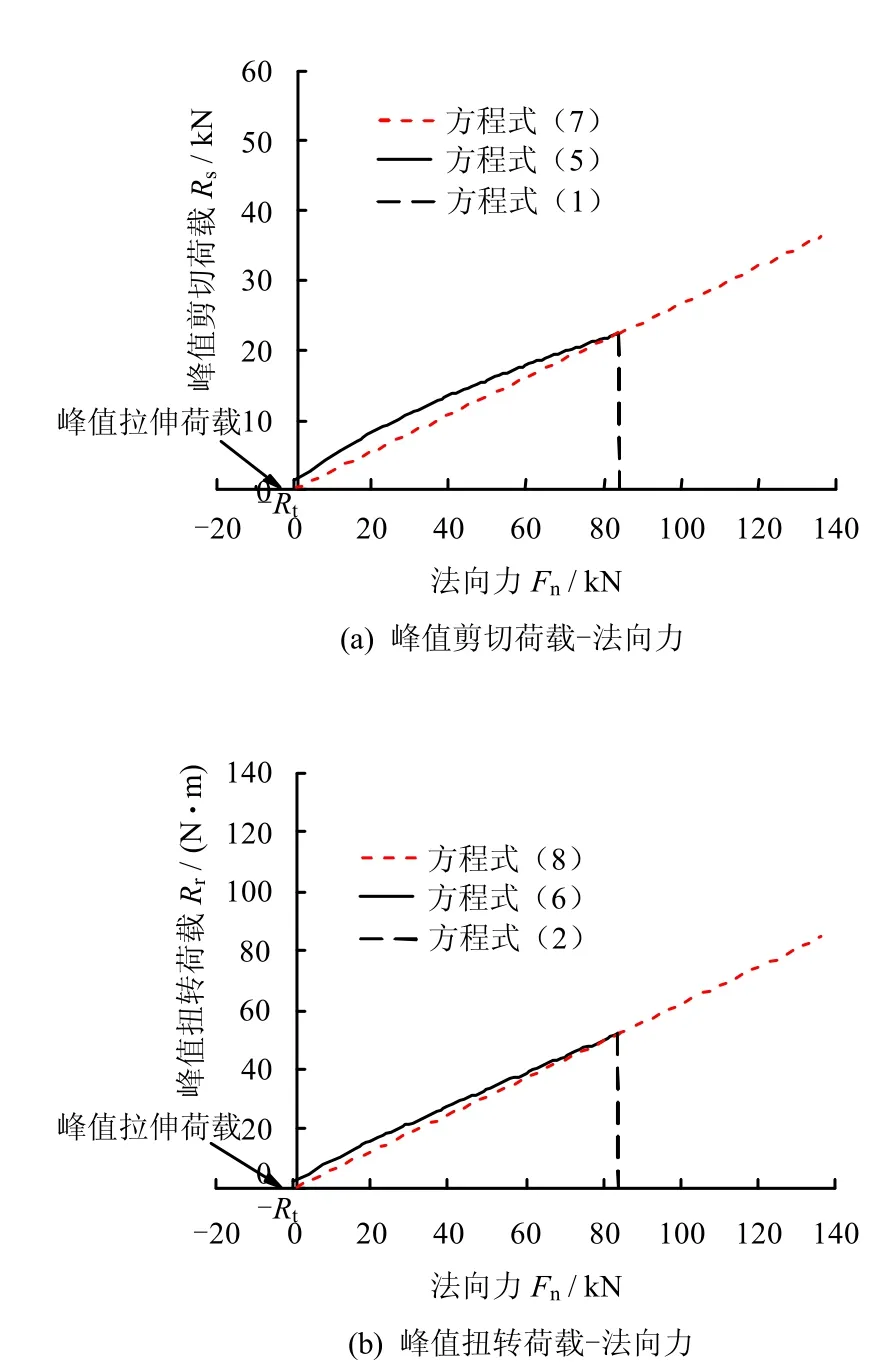
图2 无厚度的胶结颗粒的强度包线Fig.2 Strength envelope of the cemented particles with zero bond thickness

2.2 模型力学响应

蒋明镜等[31-32]首先通过严谨的理论推导，提出了颗粒胶结接触模型的力学响应，然后又经过室内试验的充分验证[26]，该力学响应能够全面而合理地反映出胶结的力学特性。

图3(a)为胶结接触模型的法向力学响应。该力学响应中，法向力随着法向位移的增加而线性增加，当拉力达到胶结峰值拉伸荷载 Rt时，胶结被拉坏，拉力突然跌落为0。图3(b)为胶结接触模型的切向力学响应。剪切力 Fs随着切向位移 us的增加首先线性增加，当达到峰值剪切荷载 Rs时，胶结发生破坏，接触点的切向力突然跌落至恒定值，该恒定值由Mohr-Coulomb 准则计算得到。图3(c)为胶结接触模型的转动向力学响应。相对转角θ 同扭矩M 近似呈线性关系，达到峰值扭转荷载 Rr之后，残余扭转荷载 Rrr由颗粒材料形状和荷载类型进行确定。

3 岩石离散元模拟试样的基本力学特性与预制双裂隙试样建模

3.1 基本力学特性

为了得到一个合理的DEM 试样，选取多个级配，生成多个不同孔隙比的试样，通过调整模型参数进行大量的模拟计算，直到试样的宏观参数与室内试验相一致为止。最终确定了一个与Lac du Bonnet 花岗岩的密实度、均匀性和力学特性相匹配的DEM 试样。该试样由15 种粒径共10 000 个颗粒组成，最大粒径为2.0 mm，最小粒径为0.5 mm。由蒋明镜等提出的分层欠压法[34]制备，制备过程中分8 层，各层孔隙比为0.215、0.213、0.211、0.209、0.207、0.205、0.203、0.200。成样后，保持侧边的墙不动，通过上下边界墙相向运动，施加给试样529 kPa 的竖向固结压力。该过程中，不断地给试样施加胶结，随着固结压力的增大，颗粒之间的接触数目增加，胶结的数目也在增加。表1为最终确定的微观胶结参数。DEM 模拟岩石试样见图4。

图3 无厚度胶结模型的力学响应[32-33]Fig.3 Mechanical responses of zero-thickness bond contact model[32-33]

表1 岩石胶结模型中采用的微观参数Table 1 Microscopic parameters used in rock bond model

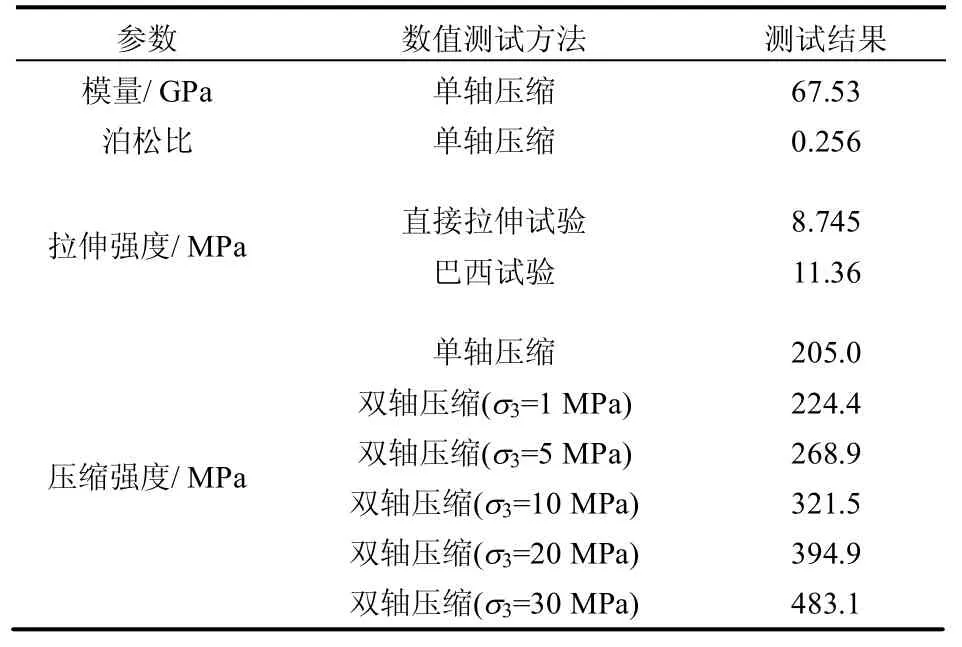
表2 DEM 数值试验得到的宏观参数Table 2 Macroscopic parameters obtained from DEM numerical tests

图4 DEM 岩石试样Fig.4 DEM rock sample

采用上述的模型和表1 中的微观参数，通过模拟直接拉伸试验、巴西试验和单双轴压缩试验，得到的宏观参数见表2。由表可见，无论是变形参数还是强度参数，数值试验得到的结果与室内试验[35-36]得到的结果一致，表明该DEM 试样与室内的试样的一致性较好。

3.2 DEM 预制裂隙试样

本文通过离散单元法模拟了含预制双裂隙的单轴压缩试验，测得了加载过程中的相关特征信息，揭示了的裂纹扩展的宏微观机理，并将裂纹的扩展路径与室内试验的实测结果相对比[7]，该室内试验所采用的试样与Lac du Bonnet 花岗岩试样的力学特性相似。

DEM 试样和预制裂隙的尺寸如图5(a)所示。由于文献[7]中的室内试样的预制裂隙通过水压穿透制成，为了与其保持一致，离散元中采用删除部分颗粒形成预制裂隙。离散元试样的尺寸为53.5 mm×106.9 mm，预制裂隙的长度为17.83 mm，比图5(b)所示的室内试样及其预制裂隙的尺寸稍小。上侧的裂隙水平方向预制，中心与试样的中心重合。垂直上侧预制裂隙向下延伸8.92 mm，即为下侧预制裂隙的上顶点，保持上顶点的位置不变，预制裂隙绕该点转动形成不同的雁式预制双裂隙，选取下侧预制裂隙与水平方向的角度α为30°、45°、60°、75°、90°五种不同的情况。

图5 含预制裂隙的岩石试样及其尺寸(单位:mm)Fig.5 Rock samples containing pre-existing flaw and its size(unit:mm)

4 双裂隙岩石的裂纹演化机理离散元分析结果

大量的岩体工程实践和试验结果表明，岩石的稳定性与裂隙的分布有很大的关系，岩石工程的失稳破坏主要是由于原有节理裂隙的演化、扩展和贯通造成的，明确岩石的破坏机理和强度特性不仅是完善岩体力学理论的需要，也是大量岩石工程实践的迫切需求。

4.1 应力-应变关系分析

图6为含不同倾角的预制双裂隙试样的应力-应变和胶结破坏数目曲线。从图中可以看出，应力-应变曲线与岩石的单轴压缩曲线类似，可分为4 个阶段，（1）初始压缩段：应力-应变关系呈线性，只有极少数的拉伸胶结破坏；（2）裂纹的稳定扩展段：随着法向荷载的增加，拉伸胶结破坏数呈线性增加，此时应力-应变曲线在超越起裂应力后进入非线性阶段；（3）裂纹的加速扩展阶段：法向荷载继续增加，拉伸破坏数加速发展，同时剪切破坏开始萌生，此阶段应力-应变曲线呈显著非线性；（4）峰后阶段：应力发生衰减，拉伸和剪切破坏快速发展，试样发生失稳破坏，此时，拉力导致的胶结破坏所占比例较大，说明大部分裂纹都是由拉力所致；胶结破坏的总数随着预制裂隙倾角的增加先减小后增加。

图7为峰值应力和裂纹的起裂应力随倾角的变化曲线。从图中可以看出，采用本文的模型进行的DEM 数值试验结果与室内结果的变化趋势比较一致，起裂应力随着预制裂隙倾角的增加，先增大，后减小，又增大，即说明30°倾角的预制裂隙使得试样最容易起裂，75°倾角的预制裂隙使得试样起裂最为困难。从峰值应力可知，30°倾角的预制裂隙对试样的强度影响最大，75°倾角的预制裂隙对试样的强度影响最小。同时，室内试验与本文的DEM 数值试验得到的起裂应力在定量上有差别，这是由于数值和室内试验测试起裂应力的方法不同所致。

4.2 双裂隙裂纹破坏后形态

表3为DEM 数值模拟得到的试样破坏形态与室内试验的对比。从表中可以看出，DEM 模拟结果与室内试验结果是比较吻合的，说明本文模型应用于模拟岩石试样的裂纹扩展规律是合理的。裂纹主要可分为两部分：（1）由下部倾斜裂隙的上端萌生，发展至水平裂隙的中部。（2）裂纹从预制裂隙的端部萌生，沿主应力方向发展，说明裂隙都是由拉应力导致的。当下部倾斜裂隙角度较小时（30°、45°）时，裂隙由水平裂隙的左端和倾斜裂隙的下端开始萌生；当下部倾斜裂隙角度为60°时，水平裂隙的两端和倾斜裂隙的下端都有裂隙萌生；当倾斜裂隙角度较大时（75°、90°），裂隙则由水平裂隙的两端萌生。造成这种现象的原因可能是岩石微观受力的差异，需要从微观上来解释裂隙的演化规律。

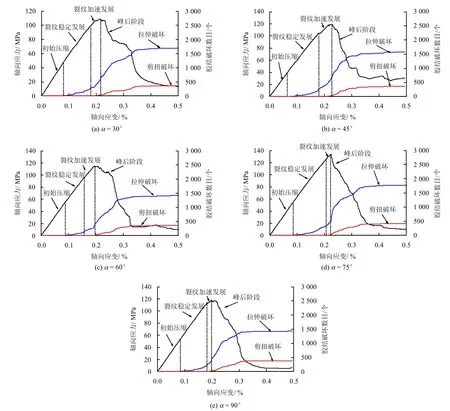
图6 DEM 数值试验得到的含不同倾角预制双裂隙试样的应力-应变和胶结破坏曲线Fig.6 Relationships between stress,number of broken bonds and strain obtained from DEM tests on rock samples containing pre-existing double flaw

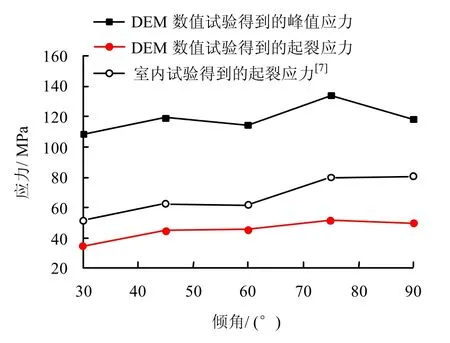
图7 DEM 数值试验和室内试验得到的峰值应力及裂纹起裂应力与预制裂隙倾角之间的关系Fig.7 Relationships between peak stress,crack initiation stress and inclination of pre-existing double flaw obtained from DEM tests and experiments

4.3 双裂隙裂纹演化机理宏微观分析

选取轴向应变为0.00、0.25 εp、0.70 εp、1.00 εp和2.00 εp所对应的各种微观信息特征图，分析裂纹的萌生、扩展和岩桥的贯通以及试样的破坏过程，并揭示试样的破坏机制，其中，轴向应变0.00为加载的起始点；轴向应变0.25 εp为胶结破坏的起始点；轴向应变0.70 εp为裂纹的起裂点；轴向应变1.00 εp为峰值应力点；轴向应变2.00 εp为峰后试样破坏点。力链图中，线条的粗细表示接触力的大小，红色代表拉力，黑色代表压力；主应力场通过布置测量圆得到，红色代表压应力，黑色代表拉应力，箭头的方向代表主应力的方向；胶结图中黑色的线表示颗粒之间的胶结；通过在接触点画一个填充的圆来代表胶结的破坏，胶结破坏点图中红色代表剪扭破坏，黑色表示拉伸破坏，这里所说的胶结拉伸破坏是指接触力大于峰值拉伸荷载 Rt所引起的胶结破坏，而胶结剪扭破坏是指接触荷载超出如图2所示的峰值强度包线所引起的胶结破坏。

表3 DEM 数值与室内试验[7]破坏形态对比Table 3 Comparison of the failures modes between the experimental[7] and DEM results

表4 含30°的预制双裂隙DEM 试样在不同应变情况下的特征Table 4 Feature maps under different strains in rock samples containing 30°pre-existing double flaw

表4为倾角30°的预制双裂隙DEM 试样在不同应变情况下的信息特征图。由图可见，当轴线应变为0.0 时，拉力集中区分布在2 个预制裂隙之间及其上下端，而水平裂隙的左右端和倾斜裂隙的下端均为压力集中区。从主应力场来看，除预制裂隙的周围外，试样的其他部分均处于双向压缩状态，且大主应力σ1朝向最大压力方向；预制裂隙的周围产生拉应力集中，在该拉应力集中区，压应力与垂直向成小角度相交，拉应力与水平向成小角度相交，该区处于拉压应力状态，而在预制裂隙的左右两端出现压应力集中，在该压应力集中区，σ1和σ3都为压应力，处于双向压缩状态。

随着轴向应力的进一步增加，拉应力逐渐增加并显著集中，当轴向应变为0.25 εp时，通过力链和主应力图可见，试样中的压应力基本保持不变，而拉应力逐渐由预制裂隙的周围向外扩散，且相应的拉应力量值增大；如与此时轴向应变对应的胶结破坏图所示，在水平预制裂隙和倾斜预制裂隙之间有2 个胶结点被拉坏，而其他区域没有发生胶结破坏。

随着轴向应力的进一步增加，当轴向应变为0.70 εp时（如胶结图所示），在预制裂隙的右端点萌生3 条裂纹，发启于水平裂隙的左右端点和倾斜裂隙的下端点，并各自朝向最大压力方向发展；从胶结破坏点可见，主要为拉力所导致的破坏，即预制裂隙的初裂主要受拉应力控制。由于裂纹的产生，拉应力逐渐释放并分配到相邻单元，相应的拉应力量值减小，且向两侧区域扩展。

当轴向应变达到1.00 εp时，预制裂隙上下端部的接触力和主应力向周围扩展，且量值减小，使得预制裂隙的左右两端的 σ3为拉应力，并与水平向成小角度相交，σ1仍为压应力，并与垂直向成小角度相交，该区域为拉压应力状态。所萌生的3 条裂纹继续朝着最大压力的方向扩展，预制裂隙之间，即水平裂隙的中部和倾斜裂隙的上端点萌生了一裂纹，连通了岩桥，从胶结破坏点图来看，该裂纹由拉力所致。

随着轴向应变的继续增加，预制裂隙上下部分的应力逐渐向外扩散，从与轴向应变为2.00 εp的力链和主应力图可见，拉应力占据了较大区域，导致预制裂隙端点萌生的裂纹朝着最大压力的方向扩展，直至贯通形成破裂面，以破裂面为分界线，左右两半试样向左右移动，应力集中释放，最终由试样的左右两半承受轴向压力。

4.4 裂纹演化方式的微观解释

通过章节4.3 的叙述可以得出结论，预制裂纹试样裂纹的发展是由裂隙周围的应力集中导致的，在裂隙的端部出现了明显的压应力集中，使之处于拉压应力状态，而裂隙的发展过程就是集中区压应力不断释放至周围单元的结果。

表5为不同预制裂隙的试样在裂纹起裂点，即应变为0.70 εp时的力链分布图。由表中力链图中可以明显地看出裂隙周围的应力集中，但当倾斜裂隙角度为30°、45°时，压应力主要集中于水平裂隙的左端和倾斜裂隙的下端；当倾斜裂隙角度为60°，水平裂隙的两端和倾斜裂隙的下端均有应力集中现象；当倾斜裂隙角度为75°、90°时，压应力主要集中于水平裂隙的两端。造成这种现象的原因可能是裂隙在主应力方向的投影长度不同导致的。

表5 裂纹起裂点力链分布图Table 5 Distribution of the force chains at the crack initiation

表6为各角度预制裂隙在主应力方向上的投影示意图。

表6 裂纹投影Table 6 Sketch of crack projection

从表6 中可以看出，当倾斜裂隙角度为30°和45°时，裂隙的投影边界为水平裂隙的左端和倾斜裂隙的下端，正是发生压应力集中的部分。这样的受力使试样中较大的部分处于拉应力状态，从而裂隙更加容易萌发。随着倾斜裂隙角度的增大，裂隙的投影变为水平裂隙的长度，倾斜裂隙对于试样受力的影响越来越不明显，试样的受拉区域越来越小，从而造成图2 中起裂应力和峰值应力总体上随预制倾斜裂隙角度的增大而增大的现象。相比于倾斜裂隙角度为90°的试样角度为75°的试样分担了一部分应力，使得其峰值荷载大于90°试样，从而峰值强度最高。

5 结 语

本文从室内实测资料提取了无胶结厚度含抗转动能力的岩石微观力学模型，并植入了离散元法（DEM）商业软件。用该软件模拟了含不同预制倾角的双裂隙岩石试样在单轴压缩作用下的裂纹扩展规律与贯通模式，揭示了裂纹扩展的宏微观机理，并将数值试验得到的裂纹扩展路径与室内试验结果进行了比较分析。结果表明，含30°的预制裂隙的岩石试样最容易起裂，含75°的预制裂隙的岩石试样最困难起裂。预制裂隙试样的失稳破坏主要是由预制裂隙之间以及端部的拉应力集中引起的。随着加载地进行，预制裂隙周围的局部拉应力增大，当应力超出材料的拉伸强度时，裂纹开始萌生。同时，轴向应力的不断增加，使得拉应力逐渐朝着试样的上下端部扩展，裂纹也朝着最大压应力的方向扩展，直至形成宏观的破裂面。最终，预制裂隙的裂纹扩展规律与室内试验结果的一致性良好。而试样的起裂荷载和峰值荷载随角度变化的规律可以用裂隙在主应力方向投影的长度来解释，投影长度越长，试样中拉应力的区域越大，造成试样越容易起裂与失稳。

[1]张志强.非贯通裂隙岩体破坏的细观特性及其宏观力学参数确定方法[博士毕业论文D].西安:西安理工大学,2009.

[2]朱维申,陈卫忠,申晋.雁形裂纹扩展的模型试验及断裂力学机制研究[J].固体力学学报,1998,19(4):355-360.ZHU Wei-shen,CHEN Wei-zhong,SHEN Jin.Simulation of experiment and fracture mechanism study on propagation of echelon pattern cracks[J].Acta Mechanica Ica Solida Sinica,1998,19(4):355-360.

[3]BOBET A,EINSTEIN H H.Fracture coalescence in rock-type materials under uniaxial and biaxial compression[J].International Journal of Rock Mechanics and Mining Sciences,1998,35(7):863-888.

[4]SHEN B,STEPANSSON O,EINSTEIN H H.Coalescence of fracture under shear stresses in experiments[J].Journal of Geophysical Research,1995,100(B4):5975-5990.

[5]LI Y P,CHEN L Z,WANG Y H.Experimental research on pre-cracked marble under compression[J].International Journal of Solids and Structures,2005,42(9-10):2505-2516.

[6]YANG S Q,DAI Y H,HAN L J,et al.Experimental study on mechanical behavior of brittle marble samples containing different flaws under uniaxial compression[J].Engineering Fracture Mechanics,2009,76(12):1833-1845.

[7]LEE H,JEON S.An experimental and numerical study of fracture coalesence in pre-cracked specimens under uniaxial compression[J].International Journal of Solids and Structures,2011,48(6):979-999.

[8]张志强,李宁,陈方方,等.非贯通裂隙岩体破坏模式研究现状与思考[J].岩土力学,2009,30(2):142-148.ZHANG Zhi-qiang,LI Ning,CHEN Fang-fang,et al.Review and status of research on failure mode of nonpenetrative fractured rock mass[J].Rock and Soil Mechanics,2009,30(2):142-148.

[9]REYES O,EINSTEIN H H.Failure mechanisms of fractured rock——A fracture coalescence model[C]//Proceedings of 7th International Congress on Rock Mechanics.Germany:Aachen,1991:333-340.

[10]TANG C A.Numerical simulation of progressive rock failure and associated seismicity[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(2):249-262.

[11]TANG C A,WONG R H C,CHAU K T,et al.Analysis of crack coalescence in rock-like materials containing three flaws—part II.Numerical approach[J].International Journal of Rock Mechanics &Mining Sciences,2001,38(7):925-939.

[12]WONG R H C,TANG C A,CHAU K T,et al.Splitting failure in brittle rocks containing pre-existing flaws under uniaxial compression[J].Engineering Fracture Mechanics,2002,69(17):1853-1871.

[13]BOBET A,EINSTEIN H H.Numerical modeling of fracture coalescence in a model rock material[J].International Journal of Fracture,1998,92(3):221-252.

[14]JIAO Y Y,ZHANG X L,ZHAO J.Two-dimensional DDA contact constitutive model for simulation rock fragmentation[J].Journal of Engineering Mechanics,2012,138(2):199-209.

[15]MI Y,ALIABADI M H.Dual boundary element method for three-dimensional fracture mechanics analysis[J].Engineering Analysis with Boundary Elements,1992,10(2):161-171.

[16]CHIOU Y J,LEE Y M,TSAY R J.Mixed mode fracture propagation by manifold method[J].International Journal of Fracture,2002,114(4):327-347

[17]POTYONDY D O,CUNDALL P A,LEE A.Modeling rock using bonded assemblies of circular particles[C]//The 2nd North American Rock Mechanics Symposium.Montreal,Quebec,Canada:[s.n.],1996.

[18]POTYONDY D O,CUNDALL P A.A bonded-particle model for rock[J].International Journal of Rock Mechanics &Mining Science,2004,41(8):1329-1364.

[19]CHO N,MARTIN C D,SEGO D C.A clumped particle model for rock[J].International Journal of Rock Mechanics &Mining Sciences,2007,44(7):997-1010.

[20]CHRISTISAN E,ROBERT S,PETER E.A discrete element model to describe failure of strong rock in uniaxial compression[J].Granular Matter,2011,13(4):341-364.

[21]蒋明镜,陈贺.岩石裂纹扩展与贯通机制的离散元数值分析[C]//2012 颗粒材料计算力学会议.大连:大连理工大学出版社,2012:328-339.

[22]蒋明镜,陈贺,刘芳.岩石微观胶结模型及离散元数值仿真方法初探[J].岩石力学与工程学报,2013,32(1):15-23.JIANG Ming-jing,CHEN He,LIU Fang.A microscopic bond model for rock and preliminary study of numerical simulation method by distinct element method[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(1):15-23.

[23]蒋明镜,白闰平,刘静德,等.岩石微观颗粒接触特性的试验研究[J].岩石力学与工程学报,2013,2(6):1121-1128.JIANG Ming-jing,BAI Run-ping,LIU Jing-de,et al.Experimental study of inter-granular particles bonding behaviors for rock microstructure[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(6):1121-1128.

[24]WONG L N Y,ZHANG X P.Size effects on cracking behavior of flaw-containing specimens under compressive loading[J].Rock Mechanics and Rock Engineering,2013,(on line).

[25]LAN H X,MARTIN C D,HU B.Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading[J].Journal of Geophysical Research,2010,115(B01202):1-14.

[26]JIANG M J,SUN Y G,LI L Q,et al.Contact behavior of idealized granules bonded in different interparticle distances:An experimental investigation[J].Mechanics and Materials,2012,55:1-15.

[27]JIANG M J,SUN Y G,XIAO Y.An experimental investigation on the contact behavior between cemented granules[J].Geotechnical and Testing Journal,2012,35(5):678-690.

[28]蒋明镜,孙渝刚,李立青.胶结颗粒接触力学特性测试装置研制[J].岩土力学,2011,32(1):309-315.JIANG Ming-jing,SUN Yu-gang,LI Li-qing.Development of experimental apparatus for contact behavior of bonded granules[J].Rock and Soil Mechanics,2011,32(1):309-315.

[29]蒋明镜,孙渝刚,李立青.复杂应力下两种胶结颗粒微观力学模型的试验研究[J].岩土工程学报,2011,33(3):354-360.JIANG Ming-jing,SUN Yu-gang,LI Li-qing.Experimental study on micro-mechanical model for two different bonded granules under complex stress conditions[J].Chinese Journal of Geotechnical Engineering,2011,33(3):354-360.

[30]蒋明镜,周雅萍,陈贺.不同胶结厚度粒间胶结微观模型参数试验研究[J].岩土力学,2013,30(5):1265-1273.JIANG Ming-jing,ZHOU Ya-ping,CHEN He.Experimental study of mechanical behaviors of bonded granules under different bond thicknesses[J].Rock and Soil Mechanics,2013,30(5):1265-1273.

[31]蒋明镜,肖俞,孙渝刚,等.水泥胶结颗粒的微观力学模型试验[J].岩土力学,2012,33(5):1293-1299.JIANG Ming-jing,XIAO Yu,SUN Yu-gang,et al.Experimental investigation on micromechanical model of cement-bonded particles[J].Rock and Soil Mechanics,2012,33(5):1293-1299.

[32]JIANG M J,YU H S,HARRIS D.A novel discrete model for granular material incorporating rolling resistance[J].Computers and Geotechnics,2005,32(5):340-357.

[33]JIANG M J,YU H S,HARRIS D.Bond rolling resistance and its effect on yielding of bonded granulates by DEM analyses[J].International Journal for Numerical and Analytical Methods in Geomechnics,2006,30(8):723-761.

[34]JIANG M J,KONRAD J M,LEROUEIL S.An efficient technique for generating homogeneous specimens for DEM studies[J].Computers and Geotechnics,2003,30(7):579-597.

[35]MARTIN C D,CHANDLER N A.The progressive fracture of Lac du Bonnet granite[J].International Journal of Rock Mechanics and Mining Sciences and Geo-mechanics Abstracts,1994,31(6):643-659.

[36]MARTIN C D The strength of massive Lac du Bonnet granite around underground openings:[Ph.D].Winnipeg,Canada:University of Manitoba,1993.