Mg2Si单轴应变的结构和电子性能

朱 岩，王冀霞，王晓昱，2

(1 河北科技师范学院物理系，河北 秦皇岛，066004；2 河北科技师范学院凝聚态物理研究所)

随着硅基微电子器件的发展，半导体金属硅化物因其组成元素资源丰富、无毒环保、热化学稳定好，抗氧化性较好等优点日益受到了重视。Mg2Si半导体因具有电阻低、Seebeck系数较高和热导低等特性，使其成为潜在的高性能的热电传感器材料，且最大工作温度可达到800 K[1]。并且，Mg2Si具有高硬度和高弹性模量的优异力学性能。因此对Mg2Si的结构、电子、热电性能和力学性能的研究一直都很受关注。目前多数研究是通过在Mg2Si化合物中掺杂其他微量元素，提高其热电性能。在半导体中掺杂元素可以改变材料的载流子浓度、载流子的迁移率、增加晶格散射，这些因素都可以改变了半导体的热性能[2～4]。诸多因素的影响使得探索Mg2Si的热电性能的物理本质带来了困难。为了更好的理解其热电性能的物理机制，笔者主要研究Mg2Si微结构的改变而引起的力学、电子性能的变化。此外，对于实际应用来说，Mg2Si多用于Si半导体晶体表面上，这样在Mg2Si与Si的界面会产生应变能，使得Mg2Si的性能与晶体有一定的差异。因此，对Mg2Si单轴应变的研究具有实际的应用意义。

1 计算方法

本次研究计算基于第一性原理密度泛函理论(DFT)的CASTEP软件包[5]。其中电子与离子实的相互作用采用超软赝势(USPP)描述，Mg和Si的价电子构型分别为2p63s2和3s23p2，各原子其他壳层的电子当作芯电子处理。对于体材料，交换关联泛函采用广义梯度近似(GGA)中的PBE方法[6]，截断能取450 eV，k点网格大小为11×11×11。系统结构优化的总能收敛精度为每个原子2.0×10-5eV，原子受力收敛至0.2 eV/nm。

Mg2Si具有反萤石结构，空间群为Fm-3m，原胞包括3个原子，其中1个Si原子占据4a(0, 0, 0)位置，其他2个Mg原子占据8c (0.25, 0.25, 0.25)的位置。根据其立方结构特点，计算过程中，对于单轴应力的模拟，选取[001]的方向作为研究对象，在考虑了单轴拉伸应力的同时还考虑了单轴压缩应力。模拟单轴拉伸和压缩过程时，所采用的模拟单元中一个边与需要施加应力的方向一致，然后改变此晶格参数模拟应变的施加。应变值为晶格参数的相对变化量，即Δc/c0=c/c0-1。其中Δc/c0>0表示对化合物施加的是压缩过程，反之施加的为拉伸过程。

2 结果与讨论

2.1 Mg2Si晶体结构

为得到Mg2Si的平衡结构，笔者首先研究了相态方程(EOS)。在平衡结构附近分别选取了不同的体积值，计算相应的总能量，然后将得到的能量-体积数据拟合三阶Birch-Murnaghan态方程[7]：

(1)

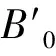
优化不同应变下的结构，图2给出的是不同应变下晶格常数a的变化。从图中可以看出，压缩过程中其晶格常数的变化比拉伸过程的变化缓慢。表明Mg2Si伸过程更易发生形变。在拉伸过程中，随着应变的增大，晶格常数降低。在应变值为0.24之前，下降呈线性趋势，且下降趋势比较平缓。之后下降趋势变得剧烈。在压缩过程中，随着应变的增加其晶格常数呈线性趋势增大。应变值为-0.20之后趋势变缓和。

图1 Mg2Si结构的总能与体积变化关系 图2 Mg2Si的晶格常数a随应变变化曲线(虚线表示应变0点位置)

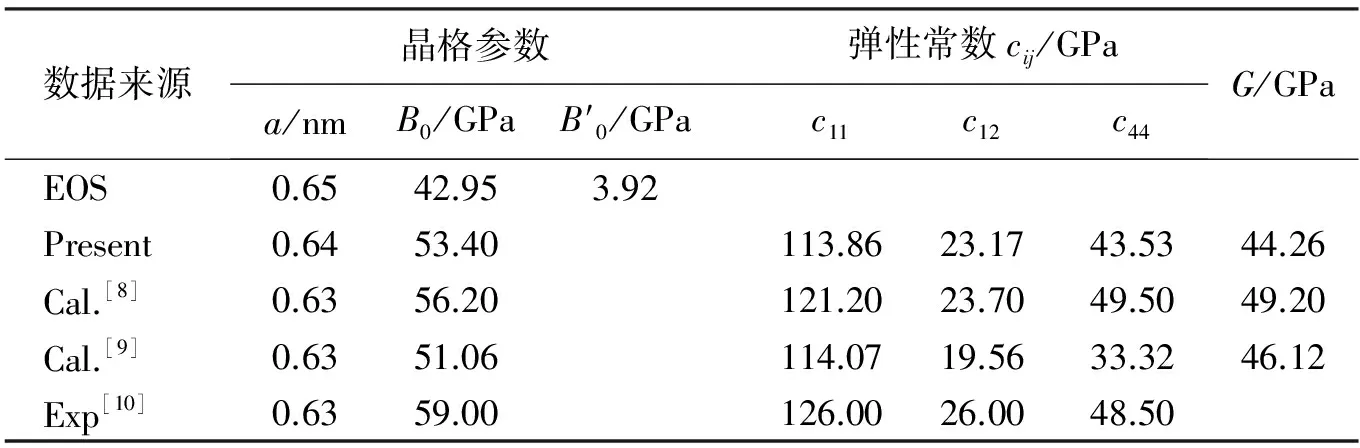
表1 Mg2Si衡结构在无应变时状态方程拟合(EOS)及优化后的晶格参数a，弹性常数cij及剪切模量G

2.2 力学性能

Q Chen等[11]曾研究了Mg2Si方同性的晶格形变对其弹性性能的影响。他们在Mg2Si空间群的不变的情况下，研究同时改变各方向的晶格参数下弹性常数的变化。笔者研究Mg2Si 沿着[001]方向的晶格参数的改变对其力学性能的影响。本次研究基于应力-应变曲线图推导出变形过程中能量、应力、弹性参数的变化规律，确定Mg2Si中的稳定范围和理想强度。Mg2Si的[001]方向的单轴应力作用下的变形过程，计算的应变范围为：拉伸Δc/c0=0～0.40，压缩Δc/c0=0～0.22。在应变的作用下破坏了Mg2Si立方结构，使其对称性发生了变化，原子的位置也相应的发生了偏移。主要是因为在应变的作用下原子之间的相互作用发生变化。优化变形后的Mg2Si发现其具有四方对称性，空间群为I4/MMM，空间群号为139。图3给出的是应力-应变曲线图。从图中可以看出，在压缩过程中，应力随应变增加而增大。而在拉伸过程中，应变值在0.24之前，随着应变值的增加，应力始终逐渐增大；而应变值大于0.24时，则随应变增加应力开始减小。为了判断在各应力下其力学性能是否稳定，在此利用Born力学稳定性判据进行判断[12]。稳定判据如下：

c44>0

(a)

c66>0

(b)

c11>∣c12∣

(c)

(d)

图3 图Mg2Si沿[001]方向的单轴应力-应变曲线(虚点线和虚线分别表示拉伸和压缩的理想强度位置，点线表示曲线极值)

图4给出了弹性常数随应变的变化曲线。可以看出，在应变值低于0.2时，弹性常数随应变值普遍降低。其中c11和c44变化幅度比较大。应变值高于0.2时，c11和c12变化幅度非常大。结合图3和图4可以看出，在拉伸应变Δc/c0=0.193时，判据中的(c)不再成立，因此此时对应的应力为[001]方向拉伸时的理想强度，即为14.5 GPa(如图3中虚线表示位置)。当压缩应变Δc/c0=0.193时，稳定性条件中的(a)不成立，应变继续增加，则结构不再稳定存在。因此，此时对应的应力26.5 GPa即为[001]方向压缩的理想强度。注意到，在拉伸和压缩过程中，应变值达到0.193时，结构才变得失稳，可见Mg2Si合物具有很好的弹性性能。

图4 Mg2Si的弹性常数随应变变化曲线(插图给出应变值0.2～0.4范围的弹性常数变化曲线)

2.3 Mg2Si电子布居

在应变的作用下Si和Mg原子s，p轨道的电子数会发生转移。在此分别选取了压缩和拉伸过程中的稳定相(Δc/c0=0.18)，及不施加应变的结构，研究Mg2Si轨道电子数随应变的变化规律。原子和化学键的布居数见表2。有电子从Mg原子转移到Si原子，表明Mg-Si之间有离子键的存在。Mg2Si平衡结构，其电子转移的最多，表明其离子性最强。单轴拉伸，压缩作用使得Mg和Si原子的位置都发生了相对移动，电子也随之转移发生了变化，使得Si和Mg原子周围的电荷发生变化。同样的应变值变化，压缩过程中，电荷变化更明显一些，主要原因是在压缩的过程中Si-Mg之间的静电场斥力更显著。此外，从表2中可以看出，Si-Mg之间电子的交叠较少，这再次说明了Si-Mg之间离子键的存在性。应变值为Δc/c0=0.18时，其化学键的键长最长，表明此时Si-Mg原子之间的作用力最弱，可以看出同样的单轴压力作用下，拉伸的作用对Mg2Si合物的结构影响更大一些。

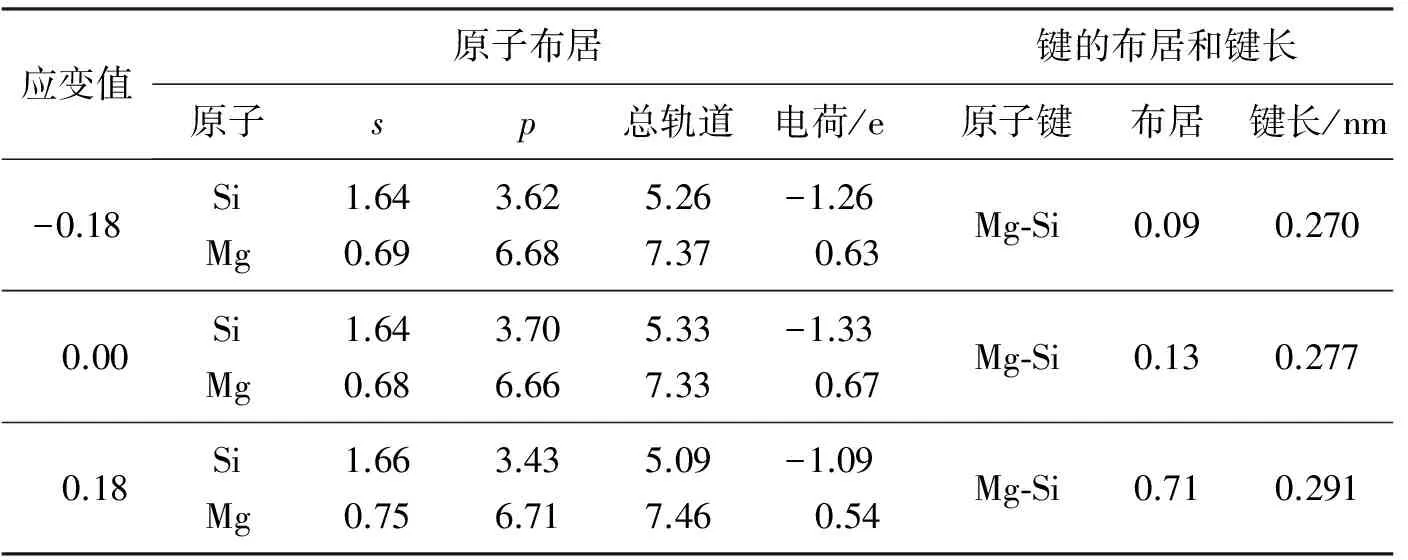
表2 Mg2Si原子布居、键的布居和键长

2.4 电子态密度

为了进一步分析Mg2Si应变下化学键和电子轨道的变化，在此给出电子态密度图(图5)。将Mg和Si原子的分波态密度与Mg2Si总的态密度对比，可以得到Mg和Si对总电子态密度的贡献。对于稳定结构，Mg2Si总的态密度在费米能级处能量较低，主要贡献是Si的p轨道电子。单轴压缩过程(Δc/c0=-0.18)，Mg2Si总的态密度在费米能级附近变化比较显著，其主要贡献为Mg的s轨道和Si的p轨道电子。在费米能级处的能量明显增大，表明其稳定性减弱。并且Mg和Si的轨道的态密度向更深能级处偏移。Si的p轨道电子较未施加应变的Si的p轨道变化明显。可见压缩作用对Si原子的影响比较大。单轴拉伸过程(Δc/c0=-0.18)，其总的态密度在费米能级处能量值增大，其主要贡献是Mg的s，p轨道和Si的p轨道电子。Mg的s，p轨道电子较未施加应变的Mg的电子轨道变化明显。可见单轴拉伸作用对Mg原子的影响比较大。

3 结 论

本次研究在密度泛函理论的框架下，用第一性原理并采用广义梯度近似 (GGA)下的交换关联泛函来研究了Mg2Si[001]方向单轴拉伸和压缩过程中的结构、力学性能和电子性质。结果表明：Mg2Si单轴拉伸应变的作用下，其晶格常数a随应变值增加而减小；压缩应变过程中，a随应变值增加而呈线性增大。通过应力-应变曲线和Born力学稳定性判据，确定Mg2Si应变作用下的稳定结构，并且表明Mg2Si有很好的弹性性能，其拉伸和压缩应变值都可达到0.193，其理想强度分别为14.5 GPa和26.5 GPa。通过Mg2Si电子布居分析，表明Si-Mg之间的显示离子键特性。通过电子态密度分析，给出Mg，Si原子轨道对Mg2Si电子密度影响。单轴压缩作用对Si原子的电子性能影响比较大，而拉伸作用则对Mg原子的电子影响较大。通过电子性质的分析，可以发现Mg2Si合物对于单轴压缩和单轴拉伸表现出不同的力学性质，其根本原因是在应变的作用下其电子性能发生了变化。

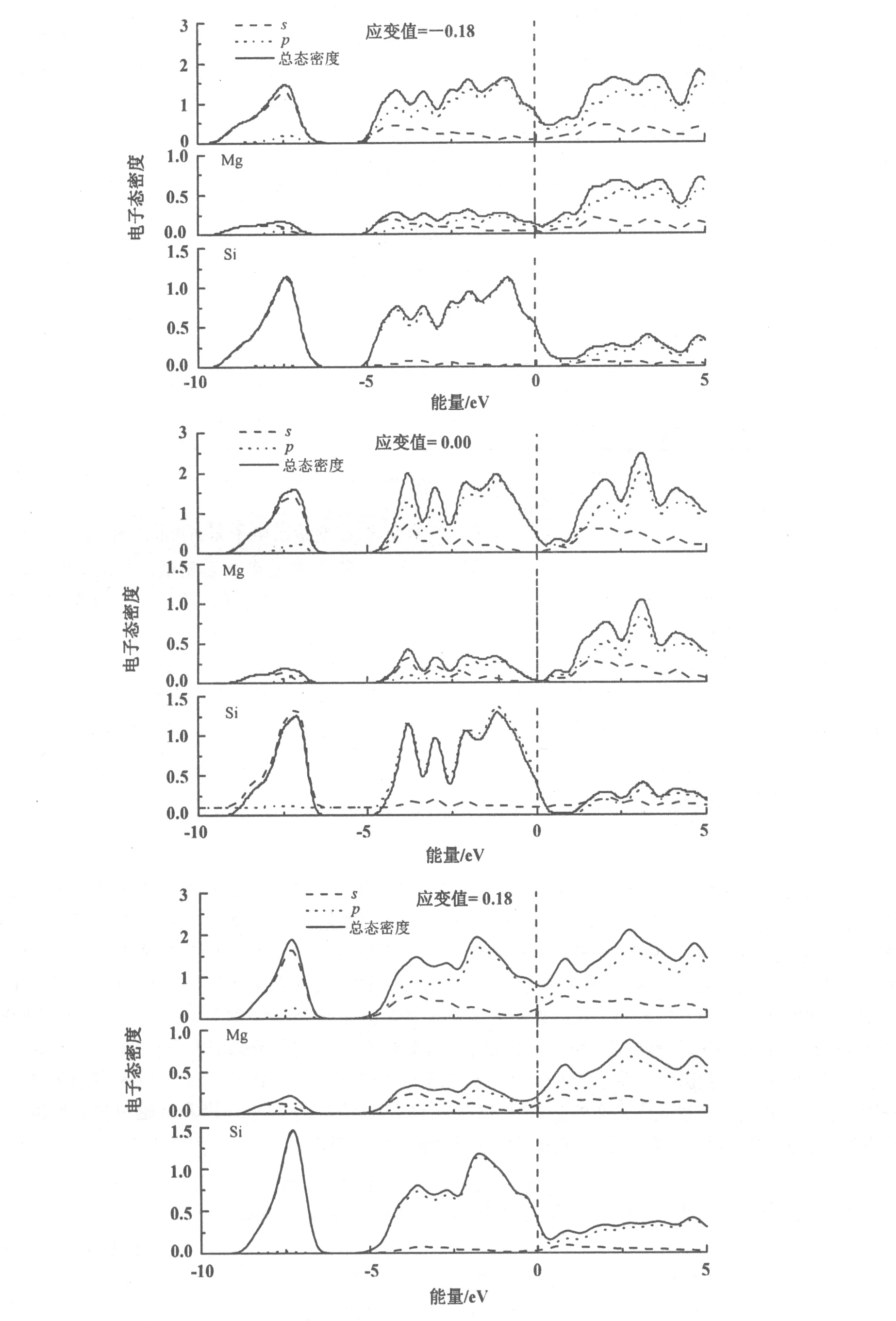
图5 不同应变下Mg2Si的态密度

[1] Q Zhang,J He,T J Zhu,et al.High figures of merit and natural nanostructures in Mg2Si0.4Sn0.6based thermoelectric materials[J].Applied Physics Letters,2008,93:102-109.

[2] T Sakamoto,T Iida,A Matsumoto,et al.Thermoelectric Characteristics of a Commercialized Mg2Si Source Doped with Al,Bi,Ag,and Cu[J].Journal of Electronic Materials,2010,39:1 708-1 713.

[3] J I Tani,H Kido.Thermoelectric properties of Sb-doped Mg2Si semiconductors[J].Intermetallics,2007,15:1 202-1 207.

[4] Q S Meng,W H Fan,R X Chen,et al.Thermoelectric properties of Sc- and Y-doped Mg2Si prepared by field-activated and pressure-assisted reactive sintering[J].J Alloys Compd,2011,509:7 922-7 926.

[5] M Segall,P J Lindan,M Probert,et al.First-principles simulation:ideas, illustrations and the CASTEP code[J].Journal of Physics:Condensed Matter,2002,14(11):2 717-2 744.

[6] J P Perdew,K Burke,M Ernzerhof.Generalized gradient approximation made simple[J].Physical Review Letters,1996,77(18):3 865-3 868.

[7] F Birch.Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K[J].Journal of Geophysical Research,1978,83(B3):1 257-1 268.

[8] J I Tani,H Kido.Lattice dynamics of Mg2Si and Mg2Ge compounds from first-principles calculations[J].Computational Materials Science,2008,42:531-536.

[9] D W Zhou,J S Liu,S H Xu,et al.Thermal stability and elastic properties of Mg2X(X=Si,Ge,Sn,Pb) phases from First-principle calculations[J].Computational Materials Science,2012,51:409-414.

[10] O Madelung,B Landolt.Numerical Data and Functional Relationships in Science and Technology,New Series,Group III,vol 17[M].Berlin:Springer-Verlag,1983.

[11] Q Chen,Q Xie,Q Q Xiao,et al.The influence of lattice deformation on the elastic properties of Mg2Si[J].Science China Physics,2013,56:701-705.

[12] R Cowley.Acoustic phonon instabilities and structural phase transitions[J].Physical Review B,1976,13(11):4 877-4 885.