小学低年级儿童的等值分数概念发展及干预*

辛自强 韩玉蕾

(1中央财经大学社会发展学院心理学系, 北京 100081) (2北京市房山区考试中心, 北京 102412)

1 问题提出

等值分数是表示具有相等值的分数(Chapin &Johnson, 2006), 例如1/2 = 2/4。它建立在分子和分母之间的乘法关系不变性前提上。等值是分数知识体系中的基础性概念, 对于学习通分、约分以及比例关系等内容具有重要意义。

国内外研究均表明, 学生普遍不能很好地掌握等值分数的概念(Mitchell & Horne, 2010; Nunes &Bryant, 2008; 苏洪雨, 2007)。国外调查发现, 有60%的四年级学生和51%的六年级学生认为10/12是5/6的2倍(Mcnamara & Shaughnessy, 2010)。我国学生的数学成绩尽管优于国外同龄者, 但同样不能很好地理解这一概念。研究发现, 五年级以上学生对等值分数的运算程序较为熟练, 但对其概念的理解比较薄弱(苏洪雨, 2007)。

新皮亚杰学派的代表人物Kamii等人(Kamii &Clark, 1995; Sophian, 2007)提出, 儿童不能理解等值分数的原因是未发展起等值分数的运算思维, 包括守恒观念和乘法思维。守恒指物体某方面的特征(如重量或体积), 不因其另一方面的特征(如形状)改变而改变(Piaget & Inhelder, 1997)。获得守恒观念的前提是对相对量的认识, 即整体的大小是由两个部分量共同决定的。乘法思维指表征某一情境的数量之间存在着确定的倍数关系(Smith, Solomon,& Carey, 2005)。乘法思维的发展也要以相对量概念的发展为基础, 尤其是要理解两个量之间的协变关系, 即两个量同向变化, 而它们之间的关系保持不变。可见, 相对量概念的发展是等值分数概念发展的基础。

Piaget和Inhelder (1975)认为, 儿童要到抽象运算阶段(11岁以后)才能获得比例守恒的概念。但后来的研究发现, 儿童很早就具有对等值分数的非符号化的理解(Siegler, Fazio, Bailey & Zhou, 2013)。McCrink和Wynn (2007)发现, 6个月大的婴儿能够正确地分辨变化了的两个因素的比例, 当重复呈现蓝点与黄点的数量比为2：1的图片时, 婴儿表现出习惯化, 而当数量比变为4：1时, 婴儿出现去习惯化。在Spinillo和Bryant (1991)的研究中, 6、7岁儿童能对由蓝白两种颜色填充的长方形模型与图片进行匹配。

对于上述现象, 学者们经过多项研究证实, 这是由于儿童具有一个直觉数学系统—— 类比数值系统(Feigenson, Dehaene, & Spelke, 2004; McCrink& Wynn, 2007; van Marle & Wynn, 2009)。在非计数的条件下, 婴儿和学前儿童能够通过该系统以近似、抽象的方式表征两个数的比。但当儿童初步发展起计数能力后, 就容易受整数等值的干扰, 当等值分数问题中有计数线索时, 倾向于使用按绝对量判断的错误策略。

为了检验这一解释, Boyer等人(Boyer, Levine,& Huttenlocher, 2008)采用橙汁浓度匹配实验, 对幼儿园至小学四年级的儿童进行考察。实验材料采用图片呈现, 每幅场景包括一个原始项和两个选项,要求被试从两杯橙汁和水的混合物中选择与原始项浓度相同的那杯。每一个杯子由两种颜色填充,分别代表橙汁和水。在一些任务中, 杯子上标有刻度以便被试能够对水和橙汁的量进行计数, 代表离散量任务, 另一些任务的杯子上未标刻度, 代表连续量任务。该实验设置了4种组间条件, 分别为：原始项和选项均为连续量; 原始项为连续量, 选项为离散量; 原始项为离散量, 选项为连续量; 原始项和选项均为离散量。结果发现, 只有原始项和选项均为离散量条件下的正确率低于随机水平, 且显著低于其他3种条件下的正确率, 其他3种条件之间无显著差异, 这表明只有在能够进行数量匹配的条件下儿童才会被误导, 儿童的错误是受整数等值的干扰造成的; 四年级的正确率显著高于二、三年级, 后者又显著高于幼儿园和一年级, 只有幼儿园和一年级的正确率低于随机水平, 这说明随着年龄的增长, 儿童解决等值分数问题的能力显著提高。

在这里, Boyer等人(2008)的研究只说明了低年级儿童容易受整数等值思维的干扰, 并没有进一步分析这反映了运算思维处于哪个水平, 也没有深入揭示低年级与高年级儿童在等值分数概念水平的差异, 以及从低年级到高年级的概念发展过程, 而这些对于指导等值分数的早期教学是具有重要意义的。Boyer等人提出, 有必要进一步探讨等值分数教学的有效方法, 可以借助儿童在连续量任务上的成功给离散量任务搭建支架, 通过两种问题的比较可能使其运用正确的直觉性加工过程而非错误的计数策略来解决离散量问题。一些教育研究者(Fuson & Abrahamson, 2005; Pitkethly & Hunting,1996)也提倡将教学与儿童的直觉性知识联系起来。这实际上体现了支架式教学的思想(Henderson,Many, Wellborn, & Ward, 2002), 它的理论基础是“最近发展区”概念(Vygotsky, 1978)。“最近发展区”是儿童独立解决问题时的实际发展水平和在他人指导下解决问题时的潜在发展水平之间的距离。因此我们需要确定儿童的等值分数概念的实际发展水平和潜在发展水平。具体来说, 各年龄儿童的运算思维处于哪个层次, 怎样促进儿童的概念水平由低向高发展, 这些问题需要结合守恒观念和乘法思维的发展来进行细致地分析和探讨。当前的研究主要聚焦于个体对等值分数的加工特点(Boyer &Levine, 2012; Meert, Grégoire, Seron, & Noël, 2012)以及小学高年级及其后阶段关于等值分数的正式教学(Fernández, Llinares, Van Dooren, De Bock, &Verschaffel, 2009; Jitendra et al., 2009; Nunokawa,2012), 很少专门探讨我国小学低年级儿童等值分数概念的理解(这时儿童尚未正式学习等值分数)以及干预方法。

本研究拟通过分析不同年龄儿童的运算思维水平来确定个体的等值分数概念发展过程, 并基于“最近发展区”理论对小学低年级儿童的守恒观念和乘法思维实施干预, 以提高其等值分数概念水平。实验1改进了Boyer等人(2008)的橙汁浓度匹配任务, 考察小学一至三年级儿童在不同数量性质条件下的正确率和策略使用情况, 以确定其运算思维水平, 在此基础上描述总体的概念发展过程, 并以此来界定各年级儿童所处的发展阶段。鉴于一年级主要学习加法思维, 二年级主要学习乘法思维,三年级初步学习分数的正式知识, 考察这3个年级的等值分数概念特点, 能够较为全面地揭示儿童的等值分数概念发展过程。在Boyer等人的研究中,连续量和离散量是通过杯子上有无刻度来区分的,但是在杯子上标刻度的情况并非完全的离散量, 因为儿童可能会忽视刻度而将其当作连续量, 即便如此也能正确解决问题。为此, 本研究中设置了一种新的离散量条件—— 将水和橙汁分别装在一个个小杯子中, 而将有刻度的情况作为混合量条件(同时提供了连续量和离散量信息), 因此共有3种数量性质条件：连续量、混合量和离散量。另外, 为考察儿童对部分和整体的加工特点, 实验设置了两种干扰条件, 一种条件是干扰项和原始项的橙汁量相等(即部分绝对量相等), 另一种条件是干扰项和原始项的橙汁和水总量相等(即整体绝对量相等)。

实验2和实验3根据每个年级儿童的实际发展水平和潜在发展水平, 设计适合其水平的干预实验,促进相应年级儿童的等值分数概念水平的发展, 以便从中概括适合特定发展阶段的干预方法; 此外,这种干预实验的结果也可用于说明实验1所得到的概念发展阶段模型的有效性。

2 实验1：儿童的等值分数概念发展特点

该实验采用3种数量性质条件下的橙汁浓度匹配任务, 考察小学一至三年级儿童的运算思维水平,并据此确定儿童的等值分数概念发展路径。

2.1 方法

2.1.1 被试

从北京市某普通小学一至三年级中随机抽取151名儿童, 其中一年级47人(男24, 女23), 平均年龄为80.86 (± 6.32)月; 二年级52人(男27, 女25),平均年龄为90.44 (± 4.28)月; 三年级52人(男27,女25), 平均年龄为104.22 (± 6.16)月。鉴于Boyer等人(2008)的研究中检测到性别差异, 本研究的3个实验中均保持了男女人数的基本平衡。

2.1.2 刺激材料和仪器

本研究采用电脑播放PPT图片的方式来呈现任务。实验仪器是17英寸彩色显示器的联想 PIV计算机, 屏幕分辨率是1024×768, 刷新频率是70 Hz。

实验材料为改编的橙汁浓度匹配任务, 给儿童呈现一杯橙汁和水的混合物(原始项), 让儿童从后面两杯(备选项)中选择与原始项的橙汁浓度相同的那杯(如图1所示)。为了便于直观比较, 杯子的下部为橙汁(黄色部分), 上部为水(蓝色部分)。设定3种数量性质的实验条件：一种是连续量条件, 仅标出橙汁和水的分界线; 一种是离散量条件, 橙汁和水分装在小杯子中; 一种是混合量条件, 在杯子上标刻度。为考察儿童对部分和整体的加工特点, 干扰选项的设置包括两种干扰条件, 一种条件是干扰项和原始项的橙汁量相等(即部分绝对量相等), 另一种条件是干扰项和原始项的橙汁和水总量相等(即整体绝对量相等)。匹配项(即答案)的橙汁和水之比等于原始项的橙汁和水之比, 但对应部分的绝对量均不相等。

3种数量性质下各有16道测验题目, 其中8题的干扰项为部分绝对量相等, 另外8题的干扰项为整体绝对量相等。为减小误差, 干扰选项与原始项之间的差值绝对量在所有的题目上大体保持一致(如表1)。表中分数值是澄汁浓度, 即橙汁/(橙汁+水)。先前研究表明“一半”是一个比较特殊的分数(Spinillo & Bryant, 1991), 因此题目中没有涉及“一半”, 并且所有的干扰项和原始项的分数值都分布在“一半”分界线两侧(即, 如果原始项的分数值小于二分之一, 那么干扰项大于二分之一, 反之亦然),这比在二分之一同侧的情况下更加简单。对所有题目的干扰项和匹配项的相对位置进行了平衡, 并对两种干扰条件下的题目的呈现顺序进行了平衡。

图1 三种数量性质的橙汁浓度匹配测验题目

表1 16道测验题目的分数值

2.1.3 实验设计和程序

实验1为3(年级：一、二、三年级)×3(数量性质：连续量、混合量、离散量)×2(干扰条件：部分绝对量相等干扰、整体绝对量相等干扰)的三因素混合设计。其中年级、数量性质属于被试间变量, 干扰条件属于被试内变量, 因变量为被试的得分(正确答题的个数)。

实验采用个别施测, 在学校的机房进行, 环境安静、光线充足。每名被试由两名主试负责, 其中一名主试给被试讲解指导语并追问, 另一名主试负责记录被试的反应以及口语报告。为增强实验材料的趣味性, 采用卡通人物“懒羊羊喝橙汁”的故事情境来讲解。首先用PPT动画给儿童演示橙汁的调制过程, 指导语如下：“懒羊羊喜欢喝橙汁, 可是它嫌橙汁太酸了, 就会往橙汁里面加一些水, 变成自己喜欢的味道。” 接着给儿童演示橙汁浓度匹配的例子, 指导语如下：“懒羊羊先调了一大杯橙汁, 喝完后还想再喝一杯同样味道的, 就又调了一小杯。”为了确保儿童理解, 演示完毕后, 让儿童再陈述一遍懒羊羊是在干什么。然后进行正式实验, 指导语如下：“现在懒羊羊遇到一个问题, 需要你帮忙解决一下。左边这杯橙汁是懒羊羊喜欢的味道, 但它不知道右边两杯中哪一杯跟左边的味道相同。你能帮它选出来吗？”待被试作出选择后, 主试追问：“为什么选这杯呢？”另一名主试记录被试的答案、口语报告, 以及在此过程中的非言语表现。

2.1.4 资料分析

各题目采取做对记1分, 做错记0分的计分方式, 计算每个被试在两种干扰条件下的得分以及总分, 并对儿童的解题策略进行编码和分析。

根据本研究中儿童的表现和口语报告, 总结出儿童在解决此类等值分数任务时使用的正确策略和错误策略类型。正确策略有6种, 分别为：知觉相似性、部分-部分比较、部分-整体比较、同增同减、部分-部分比例、同增同减比例。错误策略有5种, 分别为：部分绝对量、整体绝对量、加减运算、部分未对应、不理解题意。对各种策略的界定说明详见表2和表3。

表2 正确策略编码表

表3 错误策略编码表

结合以往研究结论, 以及本研究中不同年级儿童的表现, 将正确策略划分为3种水平。水平一是知觉相似性策略, 反映了儿童运用直觉性知识来解决问题, 在该水平上, 儿童主要依据整体性的、笼统的知觉经验来判断两个量的关系; 水平二是部分比较系列策略, 包括部分-部分比较、同增同减、部分-整体比较, 反映了儿童初级的等值分数概念,在该水平上, 儿童能够同时考虑两个量的变化来比较其关系, 但这种关系往往是简单的相对多少比较,是一种粗略的比较策略; 水平三是正式的等值分数运算策略, 包括部分-部分比例、同增同减比例, 反映了儿童运用正式的等值分数概念来解决问题, 在该水平上, 儿童能够精确计算两个量的比例关系。

由两名主试(发展与教育心理学专业的硕士)对被试的口语报告进行评估, 对照策略编码表进行策略归类。对两名主试的评估结果进行评分者信度分析, 计算Kappa系数平均值为0.91, 说明主试对策略归类的评判具有较高的一致性。

2.2 结果与分析

2.2.1 得分分析

表4列出一至三年级儿童在3种数量性质下的人数、得分的平均数和标准差, 包括在两种干扰条件下(部分绝对量相等、整体绝对量相等)的得分(满分为8)以及总分(满分为16)。

单尾

t

检验的结果表明, 在整体绝对量相等的干扰条件下, 3个年级在3种数量性质下的得分均显著高于随机水平; 在部分绝对量相等的干扰条件下, 一年级在连续量条件下、二年级在连续量和离散量条件下、三年级儿童在3种数量性质下的得分均显著高于随机水平(

ps

＜ 0.05)。以年级、数量性质为被试间变量, 以干扰条件为被试内变量, 以得分为因变量, 进行3(年级)×3(数量性质)×2(干扰条件)的重复测量方差分析。由于球形检验不成立,

df

= 0, 需校正单变量检验的自由度, 取Greenhouse-Geisser Epsilon (G-G)校正系数。重复测量变量干扰条件的主效应显著,

F

(1, 142) = 35.89,

p

＜ 0.001, η= 0.20, 整体绝对量相等的干扰条件下的得分显著高于部分绝对量相等条件下的得分(

p

＜ 0.01); 干扰条件和数量性质的交互作用显著,

F

(2, 142) = 3.87,

p

＜ 0.05, η= 0.05,简单效应分析的结果表明, 这种交互作用是次序性交互作用, 即条件变量只影响了自变量对因变量的作用程度而非方向。具体来说, 从连续量到离散量再到混合量任务, 两种干扰条件下的得分差距逐次拉大; 而部分量相等的干扰条件与整体量相等的干扰条件相比, 3种数量性质之间的差异更大。对于被试间变量, 年级的主效应显著,

F

(2, 142) = 13.88,

p

＜ 0.001, η= 0.16, 三年级的得分显著高于二年级的得分(

p

＜ 0.05), 二年级的得分显著高于一年级的得分(

p

＜ 0.01); 数量性质的主效应显著,

F

(2, 142)= 10.21,

p

＜ 0.001, η= 0.12, 连续量任务的得分显著高于离散量任务的得分(

p

＜ 0.05), 离散量任务的得分显著高于混合量任务的得分(

p

＜ 0.01)。

表4 各年级在不同实验条件下的人数、平均分及标准差

2.2.2 策略分析

为了清楚地分析儿童的策略变化, 我们对一至三年级儿童在不同数量性质条件下使用每种正确策略的频次和百分比进行统计(如表5)。频次统计依据每个被试在每道题目上的表现, 百分比的计算方法为频次/(人数×题目数)。

在连续量任务上, 3个年级运用正确策略的总频次都比较高, 卡方检验表明年级差异显著, χ=20.14,

p

＜ 0.01。3个年级均使用了水平二的策略,且使用频次最高的策略均为部分-部分比较。此外,部分一年级儿童还使用了水平一的知觉相似性策略, 部分三年级儿童还使用了水平三的两种比例计算策略。在离散量任务上, 3个年级使用正确策略的总频次有较大差异, 卡方检验表明年级差异显著, χ=40.10,

p

＜ 0.01。一、二年级都使用了水平二的部分-部分比较策略和同增同减策略, 三年级使用了水平二的3种策略以及水平三的部分-部分比例策略。在混合量任务上, 3个年级使用正确策略的总频次有较大差异, 卡方检验表明年级差异显著, χ=55.86,

p

＜ 0.01。一、二年级儿童均使用了水平一和水平二的策略, 三年级儿童则使用了水平二和水平三的策略。

对一至三年级儿童在3种数量性质下使用错误策略的频次和百分比进行统计, 方法同上, 结果如表6。

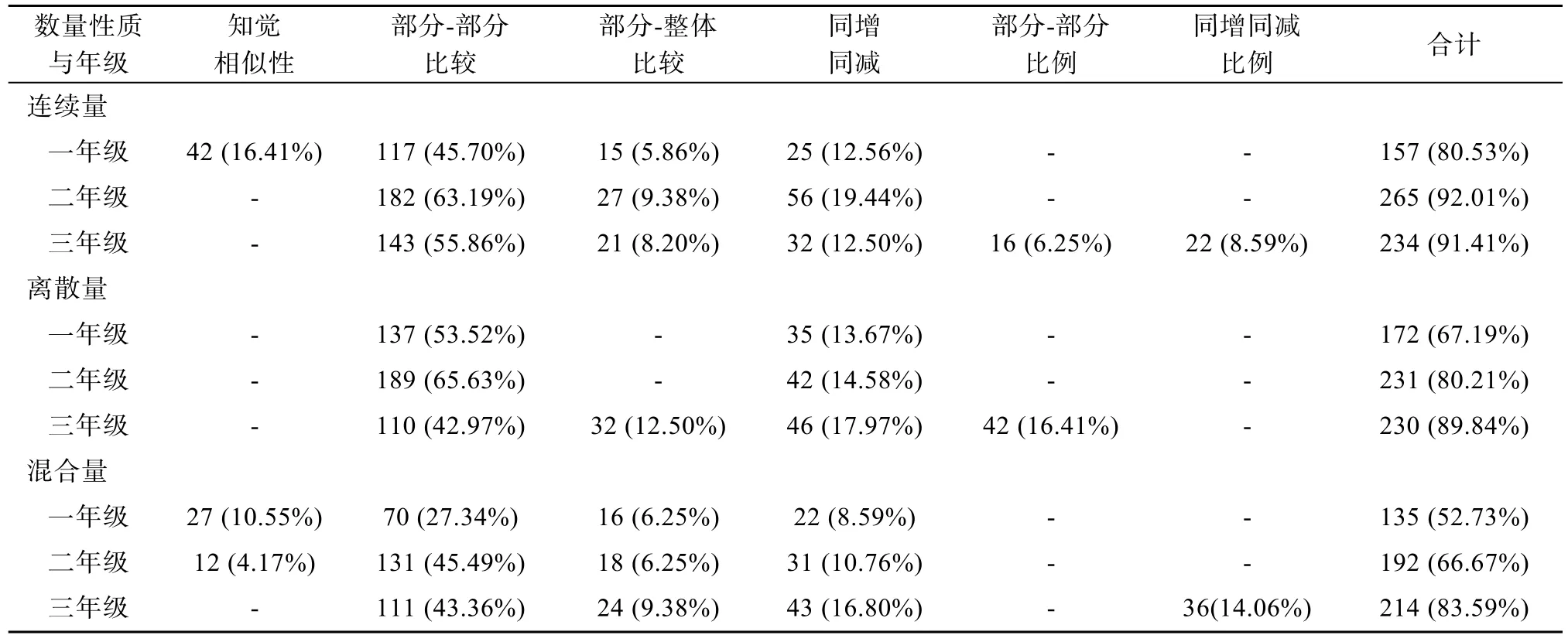
表5 一至三年级儿童在不同数量性质下使用正确策略的频次及百分比

表6 一至三年级儿童在不同数量性质下使用错误策略的频次及百分比

由表6可知, 儿童在连续量条件下出现的错误策略较少, 而在离散量和混合量条件下出现的错误策略较多; 随着年级升高, 儿童使用错误策略的频次降低。儿童使用频次较高的错误策略是部分绝对量相等和整体绝对量相等。

对各条件下每个年级的错误策略进行具体分析。在连续量条件下, 儿童的错误类型比较一致。除了有少数一年级儿童(3.13%)没有理解题意以外,3个年级儿童的错误策略均为部分绝对量相等和整体绝对量相等。在离散量条件下, 一、二年级儿童的错误策略呈现多样化特点, 均出现了部分绝对量相等、整体绝对量相等、加减运算以及不理解题目的错误, 少数二年级儿童还出现了部分未对应的错误。在混合量条件下, 一年级使用部分绝对量相等和整体绝对量相等策略的频次较高, 一、二年级使用加减运算的频次较高。

2.3 讨论

2.3.1 一至三年级儿童的等值分数概念发展特点

本实验考察了一至三年级儿童在不同数量性质的等值分数任务上的表现。得分分析表明, 儿童的表现受到数量性质的制约; 随着年级升高, 儿童的正确率显著提高。这与Boyer等人(2008)的研究结果是一致的。策略分析表明, 在3种数量性质条件下, 一至三年级儿童出现的错误主要是按绝对量进行判断, 表明他们容易受整数等值思维的干扰而作出错误选择, 从等值分数的运算思维来看, 这反映了儿童的相对量概念发展不够成熟。另外, 干扰条件对儿童的表现有显著影响, 当任务中有部分绝对量相等的干扰条件时, 比在整体绝对量相等的干扰条件下, 儿童更容易出现错误。这验证了儿童在加工过程中倾向于关注部分, 而非整体(Spinillo,2002; Spinillo & Bryant, 1991)。

下面结合不同数量性质的任务来分析各年级儿童的等值分数概念特点。连续量任务最为简单,少数一年级儿童运用了知觉相似性策略, 表明他们借助直觉性知识来解决问题。这种儿童在早期获得的、对量的相对大小的认识是基于整体量图式(global quantitative schemas) (Resnick & Singer,1993)。或者说, 儿童本来无须通过认识数, 就可以基于知觉经验初步认识两个量的关系。Sophian(2004)的研究表明, 在面积相对大小判断任务中, 5岁儿童在连续量任务上的成绩要好于离散量任务,而10岁儿童在离散量任务上的成绩要好于连续量任务, 这是由于与10岁儿童相比, 5岁儿童更少依赖计数策略。事实上, 另有研究表明, 5岁儿童即使在完成离散量的相对大小比较任务时可能也并不使用计数策略(Wing & Beal, 2004)。本研究中也体现了这一点, 在混合量任务上, 少数一、二年级的儿童采用了知觉相似性策略。

儿童获得数量化的相对量概念的时间要大大晚于获得整体量图式的时间。在需要计数的离散量任务中, 年龄较小的儿童往往只关注一个优势维度的绝对量, 而忽视另一个维度的变化, 表现出整数偏向(Ni & Zhou, 2005)。例如, Piaget和Inhelder(1975)的弹珠概率实验发现, 年龄较小的儿童是根据红色弹珠个数来判断摸到它的概率的, 没有同时考虑白色弹珠的个数。在本实验中, 一年级儿童在离散量任务上表现不理想, 出现较多的按绝对值判断的错误, 这表明他们尚未获得成熟的数量化的相对量概念。二、三年级儿童的表现较好, 能同时考虑两个数量的变化来比较其关系, 表明具有了数量化的相对量概念, 但部分二年级儿童使用了加减运算的错误策略, 这说明他们的乘法思维尚不够成熟。二年级儿童使用的正确策略为部分-部分比较和同增同减, 这在很大程度上仍依赖于加法思维。在本实验中, 为了降低任务难度, 干扰项和原始项的分数值都是位于二分之一两侧, 儿童采用这种策略有助于解决问题。

混合量任务具有双重线索, 儿童既可以忽视刻度, 将其看作连续量任务来进行判断, 也可以通过数格子, 将其看作离散量任务来进行判断, 因而导致该条件下儿童的策略不够稳定, 出错也更多。儿童在混合量任务上的表现要差于离散量, 可能有两个原因：一是从离散量任务而言, 为了避免儿童将离散量当做连续量, 将橙汁和水排成两列, 这样可能会提示儿童通过比较橙汁和水的相对多少来进行判断, 因而正确率高; 二是混合条件下的刻度线索较为突出, 容易吸引儿童进行计数, 这一点也体现在儿童的口语报告中, 但对于一、二年级的儿童而言,由于尚未掌握成熟的乘法思维, 计数后更容易采用加法思维来进行判断, 从而出现较多的错误。

值得注意的是, 在没有计数线索的连续量条件下, 仍有部分三年级儿童运用了精确的比例计算,这表明他们获得了成熟的相对量概念和乘法思维,初步具有了正式的等值分数概念。

2.3.2 儿童的等值分数概念发展阶段

相对量概念和乘法思维的发展是获得等值分数概念的基础。根据上文对一至三年级儿童的分析,我们认为等值分数概念的发展可以划分为3个阶段。第一阶段是“整体量概念”, 代表的是初步的直觉性理解, 在这一阶段儿童借助直觉性的整体量图式解决非符号化的等值分数问题。第二阶段是“数量化的相对量概念”, 在这一阶段, 儿童对相对量的认识从笼统的、直觉性的状态发展为具体的、量化的状态, 能够克服整数等值思维的干扰, 同时考虑两个维度的数量变化来进行等值判断。但由于受加法思维的限制, 经常采用相对多少比较或是加减运算, 不能进行比例运算。第三阶段是“正式的等值分数概念”, 在该阶段, 儿童发展起成熟的乘法思维, 能够同时关注两个维度, 并计算两者的比例关系。这个发展过程可表示为图2。

图2 儿童的等值分数概念发展阶段图

根据以上阶段划分, 我们可以确定小学一至三年级儿童各自所处的发展阶段。一年级儿童尚未获得成熟的数量化相对量概念, 这表明他们处于第一阶段到第二阶段的过渡期。二年级儿童在连续量和离散量任务上表现较好, 在混合量任务上表现较差,错误策略中有较多的加减运算策略, 说明二年级儿童处于第二阶段到第三阶段的过渡期, 已发展起数量化的相对量概念, 但不具有成熟的乘法思维。三年级儿童在3种数量性质条件下均表现较好, 并且一些个体能够使用比例计算策略, 表明这部分儿童发展起较为成熟的相对量概念和乘法思维, 初步获得了正式的等值分数概念。

3 实验2：对一年级儿童的相对量概念的干预研究

针对实验1的结论, 设计干预实验以促进一年级儿童的相对量概念水平的提高。根据最近发展区原理, 可以在儿童已有的整体量图式的基础上促进其数量化的相对量概念的发展。实验2(a)采用支架式教学的方法, 让儿童先进行连续量任务的练习,激活相对量表征, 再让儿童做离散量任务, 前一个任务会对后一个任务产生正迁移作用。受前一个任务的启发, 儿童在离散量任务中能够关注两部分的数量变化, 从而发展起数量化的相对量概念。

若干预实验有效果, 有可能是连续量对离散量的正迁移作用, 也有可能是任务熟悉性和练习效应。为了检验这两种猜想, 下面又设计了实验2(b)。该实验中设置两种对比条件：先做连续量任务再做离散量任务、先做离散量任务再做连续量任务。比较被试在两种条件下的成绩。如果第一种条件下被试在离散量任务上的成绩显著优于第二种条件下被试在该任务上的成绩, 而第二种条件下被试在连续量任务上的成绩与第一种条件下相比无显著差异, 就说明并非是由于任务的熟悉性导致了成绩提高。

3.1 实验2(a)

3.1.1 被试

选取与实验1的学校水平相当的另一所小学。两所学校的在校人数、师资配置和配套设施大体相当,且两校一年级的上次期末考试成绩处于同一水平。

从一年级随机选取50名被试, 随机分配到干预组和对照组, 每组各25人。干预组男生13人, 女生12人, 平均年龄为80.86 (± 6.32)月; 对照组男生14人, 女生11人, 平均年龄为83.42 (± 3.54)月。

3.1.2 刺激材料和仪器

实验仪器同实验1。

实验材料也是橙汁浓度匹配任务。干预组在干预阶段做8道连续量题目, 在正式测验中做16道离散量题目。8道连续量题目中包含部分绝对量干扰和整体绝对量干扰的题目各4道, 题目分数值见表7。16道离散量题目同实验1。对照组只做16道离散量题目。对两种干扰条件下的题目的呈现顺序进行了平衡。

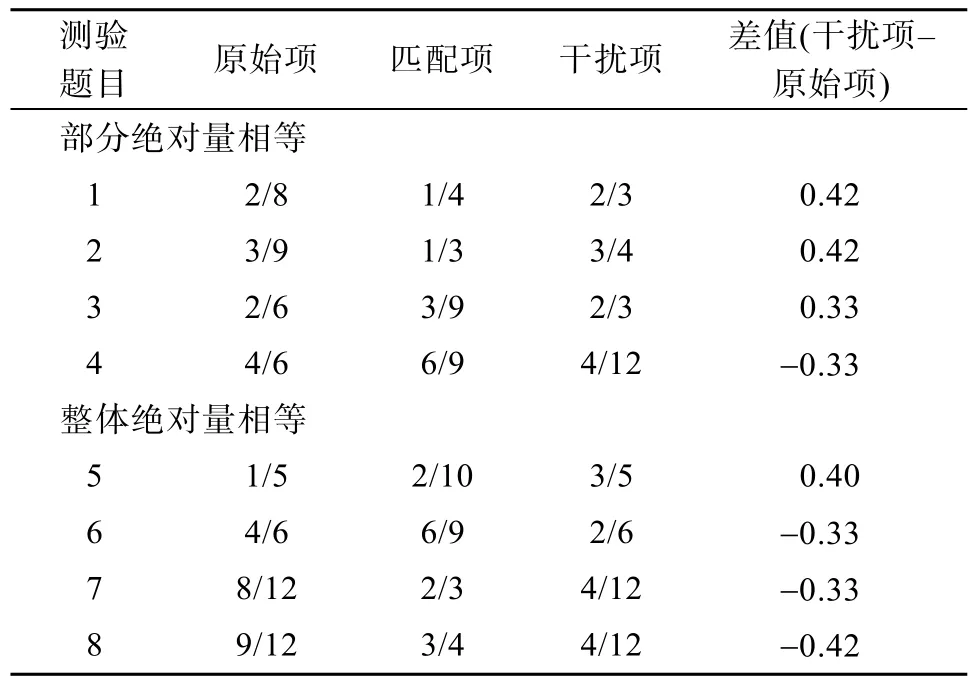
表7 8道测验题目的分数值

3.1.3 任务和程序

采用2(干预条件：有, 无)×2(干扰条件：部分绝对量相等干扰、整体绝对量相等干扰)的两因素混合设计。其中干预条件属于被试间变量, 干扰条件属于被试内变量, 因变量为被试的得分。

实验条件和指导语同实验1。干预组先做8道连续量题目, 过一小时后, 进行正式测验, 做16道离散量题目。实验组只做16道离散量题目。

3.1.4 资料编码

对被试的得分和解题策略的编码方式同实验1。对两名主试的评估结果进行评分者信度分析, 计算Kappa系数平均值为0.95, 说明主试对策略归类的评判具有较高的一致性。

3.1.5 结果与分析

首先计算干预组儿童在干预阶段的连续量任务上的得分情况。部分绝对量相等条件下的平均得分为2.95 ± 1.52(满分为4), 整体绝对量相等条件下的平均得分为3.29 ± 1.24(满分为4), 总分为6.24 ±2.21(满分为8)。

对于正式测验, 分别计算干预组和对照组儿童在离散量任务上的得分情况(表8)。对干预组和对照组的总分进行独立样本

t

检验,

t

= 2.142,

df

= 48,

p

＜ 0.05, 表明两组的总分差异显著。以干预条件为被试间变量, 以干扰条件为被试内变量, 以得分为因变量, 进行2(干预条件)×2(干扰条件)的重复测量方差分析。由于球形检验不成立,

df

= 0, 需校正单变量检验的自由度, 取Greenhouse-Geisser Epsilon (G-G)校正系数。重复测量变量干扰条件的主效应显著,

F

(1, 48) = 9.02,

p

＜ 0.01, η= 0.16; 干扰条件与干预条件的交互作用不显著,

F

(1, 48) =0.09,

p

＞ 0.05; 被试间变量干预条件的主效应显著,

F

(1, 48) = 4.59,

p

＜ 0.05, η= 0.09。

表8 干预组和对照组得分的平均数和标准差

干预组和对照组使用正确策略的情况如表9。对两组被试使用正确策略的总频次进行卡方检验,χ= 32.26,

p

＜ 0.01, 表明存在显著差异。两组被试均使用了部分-部分比较和同增同减两种策略。对照组使用部分-部分比较的频次百分比高出控制组14.75%, 在同增同减策略的使用上则差别不大。

表9 干预组和对照组使用正确策略的频次及百分比

干预组和对照组使用错误策略的情况如表10。其中使用频次最高的依然是部分绝对量和整体绝对量策略。在这4种策略上, 干预组比对照组的使用频次百分比分别下降了10%、5.5%、1%、1.75%,其中部分绝对量策略和整体绝对量策略的使用明显减少, 加减运算则变化不大。

表10 干预组和对照组使用错误策略的频次及百分比

3.2 实验2(b)

3.2.1 被试

选取与实验2(a)同一所学校的30名一年级被试, 他们均未参加实验2(a), 将其随机分配到两种条件下。先做连续量任务再做离散量任务的条件下,男生7人, 女生8人, 平均年龄81.25 (± 5.42)月; 先做离散量任务再做连续量任务的条件下, 男生8人,女生7人, 平均年龄为84.64 (± 4.54)月。

3.2.2 刺激材料和仪器

实验仪器同实验1。实验材料也是橙汁浓度匹配题目, 包括16道连续量任务和16道离散量任务。

3.2.3 任务和程序

采用组间设计, 自变量为测验顺序(先连续后离散, 先离散后连续), 因变量为被试得分。

实验指导语同实验1。一组被试先做16道连续量题目, 过一小时后, 再做16道离散量题目; 另一组被试先做16道离散量题目, 过一小时后, 再做16道连续量题目。

3.2.4 资料分析

对被试的得分和解题策略的编码方式同实验1。对两名主试的评估结果进行评分者信度分析, 计算Kappa系数平均值为0.93, 说明主试对策略归类的评判具有较高的一致性。

3.2.5 结果与分析

表11列出两种顺序条件下儿童在连续量和离散量任务上得分的平均数和标准差。对两组被试在连续量任务上的得分进行独立样本

t

检验,

t

= 0.59,

df

= 28,

p

＞ 0.05, 表明两组得分差异不显著。对两组被试在离散量任务上的得分进行独立样本

t

检验,

t

= 2.44,

df

= 28,

p

＜ 0.05, 表明两组得分差异显著,先连续后离散条件下的得分显著高于先离散后连续条件下被试的得分。

表11 两种顺序条件下被试得分的平均数和标准差

两组被试使用正确策略的频次情况如表12。在连续量任务上, 两组被试使用正确策略的频次没有显著差异, 使用的策略类型相同。在离散量任务上,两组被试使用正确策略的频次存在显著差异, χ=34.25,

p

＜ 0.001, 先连续后离散条件下的频次显著高于先离散后连续条件下的频次。

两组被试使用错误策略的频次情况如表13。在连续量任务上, 两组被试使用错误策略的频次没有显著差异。在离散量任务上, 先连续后离散条件下的被试比先离散后连续条件下的被试使用部分绝对量、整体绝对量、加减策略和不理解题意的频次百分比分别下降了10%、5.42%、0.83%、2.92%, 其中部分绝对量策略和整体绝对量策略减少得较明显, 加减运算则变化不大。

3.3 讨论

实验2(a)使用连续量任务给儿童搭脚手架, 从而促进儿童在离散量任务上的表现。结果表明, 干预组在离散量任务上的得分以及使用正确策略的总频次均显著高于对照组, 而干预组使用绝对量相等错误策略的频次比对照组有较大幅度的下降, 这说明干预组被试能够更有效地使用相对量概念进行判断。但由于干预阶段和正式测验的实验材料具有一定的相似度, 不排除被试成绩的提高是由于练习效应。为了检验这一假设, 设计并实施了实验2(b), 让一组被试先做连续量题目, 再做离散量题目, 另一组被试先做离散量题目, 再做连续量题目。结果发现, 在离散量任务上, 第一组被试的得分显著高于第二组被试的得分, 且前者比后者使用了更多的正确策略和更少的按绝对量判断的错误策略; 而在连续量任务上, 两组的得分和使用策略情况均无明显差异。这表明只有连续量任务对离散量任务具有迁移作用, 而离散量任务对连续量任务没有迁移作用, 说明被试成绩的提高不是由于练习效应造成的, 也表明个体的相对量概念确实是从低层次的整体量概念向更高层次的数量化的概念水平发展。

本实验的干预原理是依据最近发展区理论, 在原先的整体量概念的基础上促进数量化的相对量概念的发展。因为儿童的头脑中先具有了非符号的相对量图式, 通过解决连续量任务可以激活这一相对量表征, 从而对离散量任务的解决产生启发, 最终促使儿童发展起数量化的相对量概念。这是一种学习迁移。在个体原有的知识基础上建构新知识是一种有效的教学方法, 例如, Nunokawa (2012)在研究中采用双重数字线的形式, 通过类比整数数字线能够有效地促进五年级小学生对比例和百分数的学习。

在本实验中, 干预组对加减运算策略的使用与对照组差别不大, 这表明干预条件对发展乘法思维没有显著影响。

表12 两种顺序条件下使用正确策略的频次及百分比

表13 两种顺序条件下使用错误策略的频次及百分比

4 实验3：对二年级儿童的乘法思维的干预研究

针对实验1的结论, 设计干预实验以促进二年级儿童的乘法思维的发展。通过对干预组进行乘法思维的训练, 使其理解等值分数任务情境中各对应维度之间的乘法关系。

4.1 方法

4.1.1 被试

本实验与实验2是在同一所学校开展的。从二年级随机选取50名被试, 随机分配到干预组和对照组, 每组各25人。干预组男生14人, 女生11人,平均年龄为91.45 (± 5.26)月; 对照组男生12人, 女生13人, 平均年龄为90.32 (± 4.48)月。

4.1.2 刺激材料和仪器

实验仪器同实验1。

干预阶段的实验材料为8道桌椅组合题目, 呈现方式如下：首先给儿童呈现一套桌椅组合的示例图片(单人桌椅/双人桌椅/三人桌椅/四人桌椅), 然后给儿童呈现两张测验图片, 内容包含若干桌子和椅子, 问能够组成几套示例图片所示的桌椅组合。测验材料如图3所示, 左上为单人桌椅的示例图片,右上为该条件下的一张测验图片; 左下为四人桌椅的示例图片, 右下为该条件下的一张测验图片。这8道组合题目涉及的比例关系如表14所示。正式测验阶段的实验材料为16道混合量的橙汁浓度匹配题目, 对两种干扰条件下的题目的呈现顺序进行了平衡。

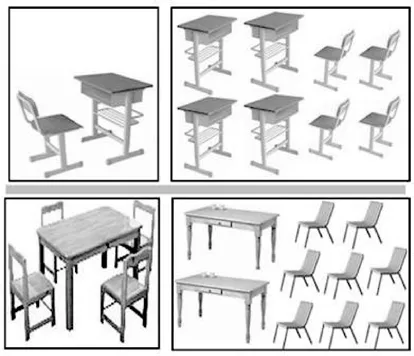
图3 桌椅组合题目示例

4.1.3 任务和程序

采用2(干预条件：有, 无)×2(干扰条件：部分绝对量相等干扰、整体绝对量相等干扰)的两因素混合设计。其中干预条件属于被试间变量, 干扰条件属于被试内变量, 因变量为被试的得分。

实验条件同实验1。

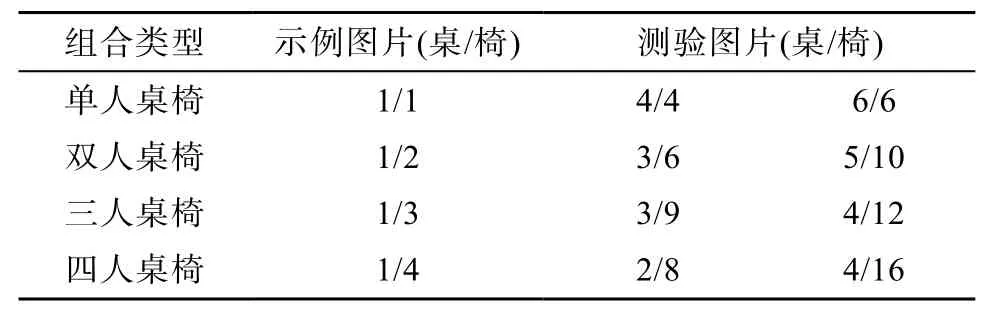
表14 8道桌椅组合题目的分数值

实验程序：对于干预组, 主试在干预阶段指导其做8道桌椅组合题目。首先播放一张示例图片,指导语为：“这是一套单人桌椅的图片, 它是由一张桌子和一把椅子组成的, 请仔细观察并记住它们的组合方式。”然后翻到下面的测试图片, 主试问：“这张图片上有一些桌子和椅子, 你看它们能组成几套刚才看到的那种单人桌椅呢？”小朋友思考并回答。如果小朋友能够回答正确则继续播放下一张,如果小朋友不能回答正确则进一步引导其思考, 告诉他一张桌子对应一把椅子, 直到其能作出正确选择。对于下面的双人桌椅、三人桌椅、四人桌椅图片, 指导语类似。当儿童不能回答正确时, 主试会对其引导, 保证儿童最终能够正确理解和回答所有题目。过一个小时之后, 进行正式测验, 主试让被试做16道混合量题目。对于对照组, 也在正式测验阶段做16道混合量题目。正式测验阶段的指导语和记录内容同研究一。

4.1.4 资料分析

对被试的得分和解题策略的编码方式同实验1。两名主试的评估结果进行评分者信度分析, 计算Kappa系数平均值为0.94, 说明主试对策略归类的评判具有较高的一致性。

4.2 结果与分析

计算干预组和对照组儿童在混合量任务上得分的平均数和标准差, 分数包括在两种干扰条件下的得分以及总分(如表15)。对干预组和对照组的总分进行独立样本

t

检验,

t

= 2.24,

df

= 48,

p

＜ 0.05,表明两组的总分差异显著。以干预条件为被试间变量, 以干扰条件为被试内变量, 以得分为因变量, 进行2(干预条件)×2(干扰条件)的重复测量方差分析。由于球形检验不成立,

df

= 0, 需校正单变量检验的自由度, 取Greenhouse-Geisser Epsilon (G-G)校正系数。重复测量变量干扰条件的主效应显著,

F

(1, 48) = 9.37,

p

＜0.01, η= 0.16; 干扰条件与干预条件的交互作用不显著,

F

(1, 48) = 0.09,

p

＞ 0.05; 被试间变量干预条件的主效应显著,

F

(1, 48) = 5.02,

p

＜ 0.05, η= 0.10。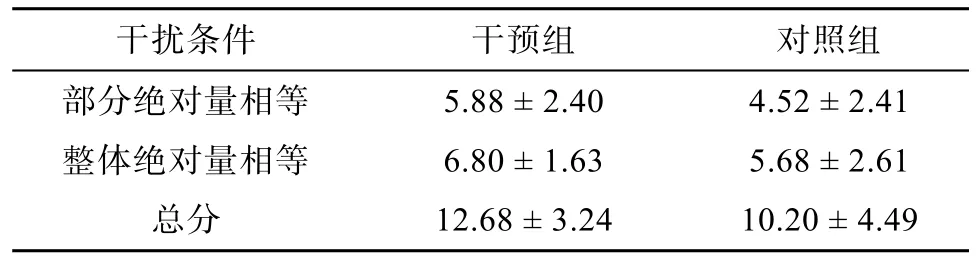

表15 干预组和对照组得分的平均数和标准差

干预组和对照组使用正确策略的情况如表16。对两组被试使用正确策略的总体频次进行卡方检验, χ= 22.89,

p

＜ 0.01, 表明存在显著差异。两组被试使用的正确策略类型存在差异。他们均使用了部分-部分比较、部分-整体比较、同增同减三种策略,三者的使用频次百分比均达到60%以上。此外, 对照组还使用了知觉相似性策略, 干预组则使用了部分-部分比例策略和同增同减比例策略。

干预组和对照组使用错误策略的情况如表17。两组被试均使用了部分绝对量、整体绝对量、加减运算这3种错误策略, 在这3种策略上, 干预组比对照组的使用频次百分比分别下降了3.25%、2.5%、8.75%, 其中加减运算策略的使用明显减少。此外,对照组有不理解题意的错误, 而干预组没有, 但干预组出现了部分未对应的错误。

4.3 讨论

实验3通过桌椅组合问题的练习来促进二年级儿童的乘法思维的发展。在这里, 乘法思维不是指单纯的乘法运算技巧, 更重要的是理解等值分数任务情境中各维度之间的倍数关系。一些研究发现,学前期甚至更小的儿童已经具有了直觉性的乘法思维(Barth, Baron, Spelke, & Carey, 2009; McCrink& Wynn, 2007; Xu & Spelke, 2000)。但小学低年级的数学教学过多训练和使用了加法思维, 这在一定程度上阻碍了儿童的乘法思维的发展。很多儿童在初学等值分数时, 依然习惯性地运用加法思维来解题(Clarke & Roche, 2009)。McCrink和Spelke (2010)提出, 后天的教学不仅要教给儿童乘法运算法则,更重要的是让儿童理解乘法问题情境的实际意义。在本实验中, 桌椅组合是乘法思维的典型情境, 对儿童而言也是熟悉的问题情境, 因而儿童容易理解。本研究的干预原理是通过让儿童对两种事物按一定的对应关系进行组合, 促进其对一种情境中两个维度之间对应数量关系的理解, 从而迁移到后面的混合量任务情境中。

结果表明, 干预组的得分和使用正确策略的频次均显著高于对照组, 且干预组的一些被试能使用比例计算策略。这是实验1的三年级儿童才能达到的水平, 表明实验3的干预确实对提高二年级儿童的乘法思维发挥了作用。在错误策略的使用上, 干预组比对照组在每种策略的使用频次上都有所减少, 其中加减运算的减少最明显, 使用频次百分比下降了8.75%, 表明干预组中只有很少的儿童采用加法思维来解决问题, 这说明干预条件能比较有效地改变儿童错误的运算思维。此外, 对照组中有不理解题意的错误, 而干预组则没有, 说明干预任务能帮助儿童理解混合量等值分数任务。需要注意的是干预组出现了部分未对应的新错误, 这可能是由于干预组过度关注题目中的数量关系, 而忽视了各部分之间的对应。例如, 已知原始项是4份橙汁对应2份水, 两者之比是2：1, 儿童看到选项中有4份橙汁和8份水时, 认为两者之比也是2：1, 所以味道一样, 而忽视了原始项的2：1是橙汁和水的关系,选项的2：1是水和橙汁的关系。这提示我们, 乘法教学不仅要教给学生运算技巧, 还要让学生真正理解乘法关系的意义。

表16 干预组和对照组使用正确策略的频次及百分比

表17 干预组和对照组使用错误策略的频次及百分比

5 总讨论

5.1 儿童的等值分数概念发展特点及干预对策

本研究首先考察了一至三年级儿童的等值分数概念发展特点, 通过分析各年级儿童的运算思维水平, 概括出等值分数概念发展的3个阶段, 接着基于“最近发展区”原理设计了两个干预实验, 分别来提高一年级儿童的相对量概念和二年级儿童的乘法思维。实验结果表明干预有效, 这也验证了等值分数概念发展三阶段理论的合理性。本研究揭示了小学低年级儿童的等值分数概念发展过程, 并对等值分数的早期教学进行了富有成效的探索, 这是对以往研究的推进。

目前很多研究者都认识到儿童的认知发展过程是连续性和阶段性的统一(Thatcher, 1991; van Dijk & van Geert, 2007)。儿童的认知发展具有质、量互变的形式。皮亚杰通过大量的实验结果区分出不同年龄儿童表现出来的不同质的特点, 并据此划分出认知发展的阶段。后继研究者通过改变任务条件, 在较低发展阶段上揭示了儿童的认知发展潜力,为认知发展的连续性提供了证据(方富熹, 方格,刘范, 1988)。

本研究将这两种研究视角结合起来, 根据对3个年级儿童的概念水平的分析, 区分出不同质的特点, 从而将等值分数的概念发展过程划分为3个阶段, 但这3个阶段并不是彼此割裂的, 而是一个连续体的不同节点。第一个阶段是整体量概念, 在该阶段儿童借助直觉性的整体量图式来解决非符号化的等值分数问题。第二个阶段是数量化的相对量概念, 在这一阶段, 儿童对相对量的认识从知觉性任务上扩展到数量化任务上, 能够克服整数等值思维的干扰, 同时考虑两个维度的数量变化来进行等值判断。但由于受加法思维的限制, 多采用相对多少比较或是加减运算, 不能进行比例运算。第三个阶段是正式的等值分数概念, 在该阶段, 儿童发展起成熟的乘法思维, 能够进行精确的比例运算。

这3个阶段与以往研究发现的儿童在解决等值分数问题时的错误类型是对应的。学者们发现, 儿童的错误主要集中在几个方面：(1)整数偏向, 指通过单独比较分子、分母或是其他的整数策略来比较两个分数(Ni & Zhou, 2005)。(2)差值比较, 指比较每个分数的分子和分母之差, 或是将每个分数与整体1相比, 来确定两个分数的比较结果。例如,Clarke和Roche (2009)发现, 当比较 5/6和7/8的大小时, 29%的六年级儿童认为两个分数是等值的,因为它们都还差一份就凑成一个整体1。(3)加法策略, 指儿童受加法思维的影响, 对等值分数所采用的加法性解释, 例如认为分子和分母加上同一个数,分数的大小不变(Behr, Lesh, Post, & Silver, 1983)。不难看出, 前两类错误是由于儿童未发展起成熟的相对量概念, 而第三类错误则是由于儿童不具有成熟的乘法思维。

实验2和实验3是对实验1所概括的等值分数概念发展阶段的延伸应用, 也是这一发展阶段的效标。实验2的干预原理是在原有的、低层次的整体量概念基础上促进较高层次的数量化的相对量概念的发展, 具体在该实验中, 是通过连续量任务给儿童搭脚手架, 从而促进其在离散量任务上的表现。为了排除任务熟悉性对干预结果的可能影响,设计了另外的检验实验, 结果表明只有连续量任务对离散量任务具有迁移作用, 而离散量任务对连续量任务没有迁移作用, 说明被试成绩的提高并非由于练习效应造成的, 也表明个体的相对量概念确实是从低层次的整体量概念向更高层次的数量化的概念水平发展, 从而验证了等值分数概念发展的第一到第二个阶段。

实验3的干预原理是通过熟悉的任务情境来促进儿童对乘法关系的实际意义的理解, 从而促进其乘法思维的发展。本实验中, “桌椅组合”是乘法思维的典型情境, 儿童较为熟悉, 也容易理解。通过让儿童对桌子和椅子按一定的对应关系进行组合,促进其对一种情境中两个维度之间对应倍数关系的理解, 进而迁移到后面的混合量任务情境中。结果发现干预组的一些二年级儿童能使用比例计算策略, 这是实验1的三年级儿童才能达到的水平,表明实验3的干预确实对提高二年级儿童的乘法思维发挥了作用, 也验证了等值分数概念发展的第二到第三个阶段。

尽管本研究取得了一些有价值的结果, 但也存在有待改进之处。本研究通过考察一至三年级儿童的概念发展特点, 概括出儿童的等值分数概念发展路径图, 这是横向比较的方法, 今后有必要采用纵向追踪或是微观发生法对这一概念发展过程进行进一步的验证。另外, 两个干预实验虽然均证明有效, 但时间均比较短, 因而还有待进一步考察这一效果的持久性。

5.2 本研究的教学实践价值及启示

本研究发现, 等值分数概念的发展是一个连续的过程, 未接受正式分数教学的低年级儿童就具有了等值分数的非正式知识, 根据各年级儿童的概念特点, 进行有针对性的干预, 能够促进儿童的等值分数概念的发展。这对于正式的分数教学具有启示意义。

第一, 尝试开展等值分数的早期教学。从小学低年级入手, 在个体的非正式的整体量基础上逐步推进对正式概念的学习, 对促进概念的掌握将是非常有意义的。例如, 对于一年级儿童, 可以在“认识物体和图形”一章中, 进行空间化等值分数任务和数量化等值分数任务的组合练习。需要注意的是,开展早期教学的任务不仅是为了促进当时的学习,而且要帮助儿童获得能支持将来学习的基本知识。因此, 不仅要考虑如何最好地达到短期教学目标,还要关注如何使儿童长远受益(Sophian, 2013)。

第二, 在教学中, 我们应更加注重概念的理解,促进实际应用。比如, 在初步学习乘除法时, 不仅让儿童学会运算法则, 也应该让儿童认识到事物之间的对应关系, 明确乘法关系所代表的意义。比如在将水果分盘时, 让儿童认识到一个果盘对应着3个水果; 在分筷子时, 让儿童明确根据一个人对应着两支筷子来分配。这是各国数学教学中普遍提出的要求。我国的《小学数学课程标准(实验稿)》明确提出数学不是空洞的抽象运算, 而应当是现实的、有意义的(教育部, 2001)。全美数学教师协会在制定课程标准时, 强调数学教学不只是发展概念和解题技能, 也应该让学生学会使用知识, 理解知识在不同情境下的意义(NCTM, 2000)。

6 结论

儿童的等值分数概念发展是连续的过程, 可分为3个阶段, 第一阶段是整体量概念, 第二阶段是数量化的相对量概念, 第三阶段是正式的等值分数概念。一年级儿童处于第一阶段到第二阶段的过渡期, 尚未获得成熟的相对量概念; 二年级儿童处于第二阶段到第三阶段的过渡期, 尚未获得成熟的乘法思维。通过整体量图式任务对离散量任务的启发,能有效促进一年级儿童获得数量化的相对量概念。通过让儿童关注等值分数任务情境中各对应维度之间的乘法关系, 能有效促儿童的乘法思维发展。

Barth, H., Baron, A., Spelke, E., & Carey, S. (2009).Children’s multiplicative transformations of discrete and continuous quantities.

Journal of Experimental Child Psychology, 103

, 441-454.Behr, M., Lesh, R., Post, T., & Silver, E. (1983). Rational number concepts. In R. Lesh & M. Landau (Eds.),

Acquisition of mathematics concepts and processes

(pp.91-125). New York： Academic Press.Boyer, T. W., & Levine, S. C. (2012). The development of proportional scaling： Is 1/3= 2/6 = 3/9 = 4/12?

Journal of Experimental Child Psychology, 111

, 516-533.Boyer, T. W., Levine, S. C., & Huttenlocher, J. (2008).Development of proportional reasoning： Where young children go wrong.

Developmental Psychology, 44

(5),1478-1490.Chapin, S. H., & Johnson, A. (2006).

Math matters:Understanding the math you teach, grades K-8

(2nd ed.).Sausalito, CA： Math Solutions.Clarke, D. M., & Roche, A. (2009). Students’ fraction comparison strategies as a window into robust understanding and possible pointers for instruction.

Educational Studies in Mathematics, 72

, 127-138.Fang, F. X., Fang, G., & Liu, F. (1988). Cognitive development：Towards a combined theory of continuity and stages.

Acta Psychologica Sinica, 20

(1), 3-9.[方富熹, 方格, 刘范. (1988). 略论儿童认知发展是阶段性和连续性的统一.

心理学报, 20

(1), 3-9.]Feigenson, L., Dehaene, S., & Spelke, E. S. (2004). Core systems of number.

Trends in Cognitive Sciences, 8

(7),307-314.Fernández, C., Llinares, S., Van Dooren, W., De Bock, D., &Verschaffel, L. (2009). The effect of the number structure and the quantity type on secondary school students’proportional reasoning. In M. Tzekaki, M. Kaldrimidou, &H. Sakonidis (Eds.),

Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics education

(Vol. 3, pp. 25-32). Thessaloniki, Greece.Fuson, K. C., & Abrahamson, D. (2005). Understanding ratio and proportion as an example of the apprehending zone and conceptual-phase problem-solving models. In J. Campbell(Ed.),

Handbook of mathematical cognition

(pp. 213-234).New York： Psychology Press.Henderson, S. D., Many, J. E., Wellborn, H. P., & Ward, J.(2002). How scaffolding nurtures the development of young children’s literacy repertoire： Insiders’ and outsiders’collaborative understandings.

Reading Research and Instruction, 41

, 309-330.Jitendra, A. K., Star, J. R., Starosta, K., Leh, J. M., Sood, S.,Caskie, G., … Mack, T. R. (2009). Improving seventh grade students’ learning of ratio and proportion： The role of schema-based instruction.

Contemporary Educational Psychology, 34

(3), 250-264.Kamii, C., & Clark, F. B. (1995). Equivalent fractions： Their difficulty and educational implications.

Journal of Mathematical Behavior, 14

, 365-378.McCrink, K., & Spelke, E. S., (2010). Core multiplication in childhood.

Cognition, 116

, 204-216.McCrink, K., & Wynn, K. (2007). Ratio abstraction by 6-month-old infants.

Psychological Science, 18

, 740-745.Mcnamara, J., & Shaughnessy, M. M. (2010).

Beyond pizzas &pies: 10 essential strategies for supporting fraction sense,grades 3-5

. Sausalito, CA： Math Solutions.Meert, G., Grégoire, J., Seron, X., & Noël, M. (2012). The mental representation of the magnitude of symbolic and nonsymbolic ratios in adults.

The Quarterly Journal of Experimental Psychology, 65

(4), 702-724.Ministry of Education. (2001).

Full-time compulsory education mathematics curriculum standard

(pp. 59-63).Beijing： China： Beijing Normal University Press.[教育部. (2001).

全日制义务教育数学课程标准

(pp.59-63). 北京： 北京师范大学出版社.]Mitchell, A., & Horne, M. (2010). Gap thinking in fraction pair comparisons is not whole number thinking： Is this what early equivalence thinking sounds like? In L. Sparrow,B. Kissane, & C. Hurst (Eds.),

Shaping the future of mathematics education

(Proceedings of the 33rd annual conference of the Mathematics Education Research Group of Australasia, pp. 414-421). Fremantle： MERGA.National Council of Teachers of Mathematics (NCTM). (2000).

Principles and standards for school mathematics

. Reston,VA： Author.Ni, Y. J., & Zhou, Y. D. (2005). Teaching and learning fraction and rational numbers： The origins and implications of whole number bias.

Educational Psychologist, 40

, 27-52.Nunes, T., & Bryant, P. (2008). Rational numbers and intensive quantities： Challenges and insights to pupils’implicit knowledge.

Anales de Psicologia, 24

(2), 262-270.Nunokawa, K. (2012). Multi-relation strategy in students’ use of a representation for proportional reasoning.

Eurasia Journal of Mathematics, Science & Technology Education,8

(4), 233-248.Piaget, J., & Inhelder, B. (1975).

The origin of the idea of chance in children

. New York： Norton. (Original work published in 1951).Piaget, J., & Inhelder, B. (1997).

The child’s construction of quantities: Conservation and atomism.

London： Routledge.Pitkethly, A., & Hunting, R. (1996). A review of recent research in the area of initial fraction concepts.

Educational Studies in Mathematics, 30

, 5-38.Resnick, L. B., & Singer, J. A. (1993). Protoquantitative origins of ratio reasoning. In T. Carpenter, E. Fennema, & T.Romberg (Eds.),

Rational Numbers: An Integration of Research

(pp. 107-130). Hillsdale, NJ： Lawrence Erlbaum Associates.Siegler, R. S., Fazio, L. K., Bailey, D. H., & Zhou, X. L.(2013). Fractions： The new frontier for theories of numerical development.

Trends in Cognitive Science, 17

(1),13-19.Smith, C., Solomon, G., & Carey, S. (2005). Never getting to zero： Elementary school students’ understanding of the infinite divisibility of number and matter.

Cognitive Psychology, 51

, 101-140.Sophian, C. (2004). A prospective developmental perspective on early mathematics instruction. In D. H. Clements, J.Sarama, & A. M. DiBiase (Eds.),

Engaging young children in mathematics: Standards for early childhood mathematics education

(pp. 253-266). Mahwah, NJ： Lawrence Erlbaum Associates.Sophian, C. (2007).

The origins of mathematical knowledge in childhood

. New York： Lawrence Erlbaum Associates.Sophian, C. (2013). Vicissitudes of children's mathematical knowledge： Implications of developmental research for early childhood mathematics education.

Early Education &Development, 24

(4), 436-442.Spinillo, A. G. (2002). Children's use of part-part comparisons to estimate probability.

Journal of Mathematical Behavior,21

(3), 357-369.Spinillo, A. G., & Bryant, P. (1991). Children’s proportional judgments： The importance of “half”.

Child Development,62

, 427-440.Su, H. Y. (2007). Investigation on learning fractions of students of grade seven.

Journal of Mathematics Education,16

(4), 48-51.[苏洪雨. (2007). 七年级学生分数学习情况的调查研究.

数学教育学报, 16

(4), 48-51.]Thatcher, R. W. (1991). Maturation of the human frontal lobes：Physiological evidence for staging.

Developmental Neuropsychology, 7

(3), 397-419.van Dijk, M., & van Geert, P. (2007). Wobbles, humps and sudden jumps： A case study of continuity, discontinuity and variability in early language development.

Infant and Child Development, 16

(1), 7-33.van Marle, K., & Wynn, K. (2009). Infants’ auditory enumeration： Evidence for analog magnitudes in the small number range.

Cognition, 111

, 302-316.Vygotsky, L. S. (1978). Interaction between learning and development (M. Lopez-Morillas, Trans.). In M. Cole, V.John-Steiner, S. Scribner, & E. Souberman (Eds.),

Mind in society: The development of higher psychological processes

(pp.79-91). Cambridge, MA： Harvard University Press.Wing, R. E., & Beal, C. R. (2004). Young children’s judgments about the relative size of shared portions： The role of material type.

Mathematical Thinking and Learning, 6

(1),1-14.Xu, F., & Spelke, E. S. (2000). Large number discrimination in 6-month-old infants.

Cognition, 74

, B1-B11.