基于VB的水准网经典平差系统的开发与应用

张广宇，欧阳兆灼，那福超，杨 帆

（1.中国地质大学 （北京）地球科学与资源学院，北京100083；

2.中国地质调查局沈阳地质调查中心，辽宁 沈阳 110034）

基于VB的水准网经典平差系统的开发与应用

张广宇1，2，欧阳兆灼2，那福超2，杨 帆2

（1.中国地质大学 （北京）地球科学与资源学院，北京100083；

2.中国地质调查局沈阳地质调查中心，辽宁 沈阳 110034）

根据水准网数据特征，按已知数据、观测数据以及水准网边和点的相对位置关系设计了数据组织结构。基于间接平差模型，在VB环境下设计开发了水准网平差系统。选取了一组水准网数据，计算了水准网的高程平差值、高程中误差、高差平差值和高差中误差，并与已有计算结果作了对比，验证了程序编制的正确性和系统运行的可靠性。

水准网；间接平差；中误差；VB；高差

水准测量是建立高程控制的一种常规方法，也是高精度沉降监测的主要手段之一。为提高水准测量的效率，不但需要采用更加科学、快速的作业模式，而且需要采用简便、可靠的平差处理软件。间接平差以其误差方程具有较强的规律性，便于编制程序解算等特点，应用越来越广泛，是水准网平差程序编写的主要模型［2－6］。本文采用 Visual Basic［7］语言设计开发了经典水准网平差系统，简要介绍了水准网数据组织、算法实现及系统的基本功能，通过试验数据处理与分析，验证了程序编制的正确性和系统运行的可靠性。

1 间接平差原理与数据组织

1.1 间接平差原理

间接平差［8－10］的误差方程形式统一，规律性较强，便于程序编制，且所选参数往往就是平差后所需的最后成果。通过选定t个独立参数，将每个观测量分别表达成这t个参数的函数，建立函数模型，按最小二乘原理，用求自由极值的方法解出参数的最或然值，从而求得各观测量的平差值。其函数模型见式（1）。

1.2 数据组织

水准网根据其网形可分为附合、闭合和支水准等几种形式。其中应用最广的为附合和闭合水准网，不管何种网形，一条水准路线包括四个起始数据：起始点、高差、距离、终点，且边具有方向性。因此在进行水准网数据结构设计中，必须体现出起点、终点，从而判断其与高差的关系。为编程方便，遵循如下两条原则：①各高程点的编号从小到大按自然数的顺序编码，不可重复也不可缺少；②已知点编码优先于待定点，靠近已知点的编码要尽量小。在综合分析水准网特征及程序设计的基础之上，将水准网数据结构组织见图1。

图1 水准网数据结构组织

2 算法实现

2.1 平差计算步骤

水准网间接平差以测段高差为平差元素，程序需具备计算高程平差值、单位权中误差、任意点高程中误差和测段高差中误差的功能，平差计算步骤如［7－9］：①计算未知点近似高程；②列出误差方程及条件方程，组成法方程；③解算法方程，求得高程改正数；④计算高程平差值；⑤如果高程改正值中的绝对值最大的一个小于给定的阈值，则平差计算结束，否则由新的近似高程值再一次平差，重复步骤②、③、③、⑤；⑥精度评定。

2.2 近似高程推算

待定点的高程计算是为了得到未知点的近似高程。首先定义水准路线起点和终点端点号数组QDH（k）、ZDH（k） （k为观测高差个数），其次需要定义一标志数组ZDH（z） （z为总点数），用来标识该点是否为已知点、未知点和已计算过的点。当ZDH（z） ＝1时，说明第i点的高程已知或已计算，ZDH（z） ＝0时，说明第i点待计算。如果该两点有一点是已知或已计算出的，而另一点未知，则可由其中已知高程点与未知点间的观测高差计算得到未知点的近似高程。为了防止由于编号不当或观测值排列顺序的限制而一次不能完全推算出所有的待定点，需采用多次推算的方法来解决。

2.3 误差方程和法方程的组成

2.3.2 权值的确定

当观测精度相等时，观测值的精度与观测路线长度的平方根成正比，权与路线长度成反比，见式（9）。

式中Sij为观测高差路线长。

2.3.3 法方程的组成

在间接平差中，法方程的系数矩阵是对称正定的稀疏矩阵，为了提高计算效率，可只存放其包括主对角线的下三角元素，并存放在法方程的系数数组FFCXS（t＊（2t＋1））（其中t为未知点点数）中，依次存放元素［Paa］、［Pba］、［Pbb］、［Pca］、［Pcb］、［Pcc］……

高差观测值的误差方程式的一般形式见式（10）。

每列出一个误差方程式后，对其立即法化处理，并处理i和j点是否为已知点。必须注意的是，每个误差方程式最多只能有三个法方程式的系数（［Paa］、［Pab］（或［Pba］）、［Pbb］）和两个常数项（［Pal］和［Pbl］），将其分别累加于法方程的系数数组FFCXS（t＊（2t＋1））和法方程的常数数组FFCCS（m＋1）（其中m为总点数）的相应单元，当所有的误差方程式都法化后组成最终的法方程系数和对应的常数项。最后，调用高斯约化程序解算法方程。

2.4 精度评定

精度评定是为了进行水准网优化设计和衡量观测成果，以使控制网满足一定的要求以及便于成果的合理利用。精度评定的程序和法方程组成的程序几乎一样，只是常数项不同而已，在精度评定中未知数常数项系数恒为1，可以借助误差方程式列立部分得到。

3 系统设计

为了便于水准网测量数据的管理，设计了水准网测量数据库，并基于数据库架构了系统。系统在整体设计上，将每个水准网按项目处理，给定全局唯一编号，即项目编号，项目编号由年（四位）月（两位）日（两位）和三位顺序编码组成，顺序编码由系统自动分配，确保了项目编号的唯一性。

在数据库设计上，共划分了项目列表、已知（概略）点表名称、测段信息表、近似高程表、测段路线权值表、法方程系数表、法方程常数和解、高程平差值、高差改正表、单位权中误差表、高程中误差表、高差中误差表和计算设置表，各表通过项目编号进行关联。

在功能上，除了平差计算外，还具备原始数据导入、数据备份、数据还原、输出平差报告为 Word文件和系统设置等功能，在原始测量数据录入方面，可以按项目向导逐步录入数据。也可将原始测量数据整理为文本文件，选择数据导入功能，系统自动分类数据并存储到数据库中，执行平差计算，自动生成水准网平差报告。

系统主界面如图2所示，系统结构和数据处理流程如图3和图4所示。

图2 系统主界面

4 实例验证

为了验证系统平差计算的正确性和系统运行的稳健性，选取了一组水准网数据［11］进行计算验证。Y1、Y2、Y3为已知点，W1、W2、W3为未知点。水准网网图如图5所示，水准网数据见表1和表2。

表1 已知点高程值

将上述水准网数据整理成本文规定的数据格式，另存为文本文件，直接导入系统便可进行平差计算，也可以按系统提供的平差向导逐步录入数据，再进行计算。

表2 高差和路线长度

经计算，水准网单位权中误差为2.147mm，未知点高程平差值、未知点高程中误差和测段高差中误差间见表3和表4。程序计算结果与原结果一致，说明程序设计的正确性。

图3 系统结构

图4 数据处理流程

图5 水准网网图

表3 高程平差值和中误差

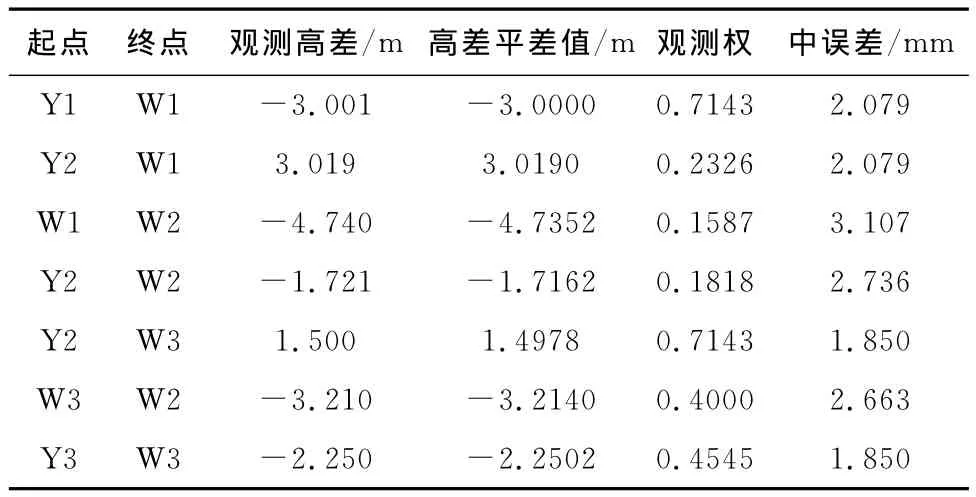
表4 高差平差值和中误差

5 结束语

本文基于间接平差模型，在VB环境下设计开发了水准网平差系统，并以实例进行了验证，算法程序编写正确，系统设计合理，运行稳健，具有很高的实用性。

1）分析了水准网数据特征，根据已知数据、观测数据以及水准网边和点的相对位置关系设计了水准网间接平差计算所需的数据结构。

2）建立了水准测量数据库，实现了对地质测绘中水准测量数据的统一管理。

3）系统功能丰富，可按文本文件形式导入水准网数据，系统自动将数据写入对应的数据表，也可按平差计算向导逐步录入水准网数据。系统还具备数据备份、数据还原以及输出平差报告为Word文件等诸多功能。

［1］万里红.“3S”技术在西藏阿里机场工程地质勘察中的应用研究［D］.成都：成都理工大学，2007.

［2］陈本富，邹自力.基于VB6.0的加权自由水准网平差程序的开发［J］.测绘科学，2009，34（11）：161－162.

［3］梅连辉，郭际明，周命端，等.基于VB平台的水准网平差软件开发研究［J］.测绘信息与工程，2011，36（6）：32－34.

［4］李巍，赵亮，张占伟.基于VC的水准网平差程序的设计与研究［J］.测绘通报，2013（5）：20－22.

［5］周长江，顾和和.基于VB环境下水准网平差程序设计研究［J］.现代测绘，2012，35（1）：12－14.

［6］张美微，余学详，邓蓉蓉，等.基于VB的水准网平差软件的设计与实现［J］.北京测绘，2011（1）：78－80.

［7］常晓波，刘颖.Visual Basic 6.0高级编程编辑［M］.北京：清华大学出版社，2004.

［8］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉：武汉大学出版社，2003.

［9］宋力杰.测量平差程序设计［M］.北京：国防工业出版社，2009.

［10］葛永慧，余哲，刘志德.测绘编程基础［M］.北京：测绘出版社，2002.

［11］全国测量学辅助教材编委会.测量学习题集［M］.北京：测绘出版社，1991.

Exploiture and application of classical adjustment system of elevation net based on VB

ZHANG Guang－yu1，2，OUYANG Zhao－zhuo2，NA Fu－chao2，YANG Fan2
（1.School of Earth Sciences and Resources，China University of Geosciences（Beijing），Beijing 100083，China；2.Shenyang Institute of Geology and Mineral Resources，China Geological Survey，Shenyang 110034，China）

On the basis of the data structure designed，according to the known data，observation data and the relation of points and lines by the characteristics of the leveling net.Using VB to code，designes and developes an adjustment system of levelling net，based on indirect adjustment model.Choosing a set of levelling net data to calculate adjusted value and mean square error of elevation and elevation difference，and makes a comparison with existing results，and verification the validity of the programming and the reliability of the system.

leveling net；indirect adjustment；mean square error；VB；elevation

欧阳兆灼（1979－），女，汉族，吉林松原人，硕士研究生，工程师，主要从事地质矿产及测绘工作。

P207

A

1004－4051（2014）S2－0354－04

2014－08－4

中国地质调查局项目“东北地区地质矿产调查评价进展跟踪与工作部署研究”资助（编号：1212011220845）

张广宇（1981－），男，满族，辽宁抚顺人，在读博士研究生，高级工程师，主要从事“3S”技术集成与地质测绘方面的研究。E－mail：157613090＠qq.com。