短波天线常见问题分析
国家无线电监测中心哈尔滨监测站 罗士伟
短波天线常见问题分析
国家无线电监测中心哈尔滨监测站 罗士伟
随着信息技术的不断发展,在短波天线通信方式上也发生了巨大的改变。其中在阵元间隔距离进行简化分析,选取适当的距离作为短波天线的放置位置。此外在阻抗值选定范围上,尽量保证馈线和无线电发射机的阻抗值一致,这样才能减少原有功率的损耗。笔者在此进行了详细的分析,以便于提供可参考性的依据。
短波天线;阻抗值;功率损耗
引言
在原有模式中短波天线在传输效应模式上具有一定的限制因素,其中包括:选取距离的限制因素,极限距离与传输频段成反比关系,当频段无限增大时,便会造成极限距离的缩短。此外在抗阻因素上也没有进行详细的划分,造成大气层产生的无线电流与天线产生的电流产生共轭效应。而现代模式中的传输模式具有新型转化阶段,解决了短波天线的常见问题。
1.短波传输损耗方式
1.1 地波传输损耗
短波的传输方式有多种,其中包括:地波传输和天波传输,地波传输损耗功率较小,短波在遇到障碍物时,会将辐射源传输至导电地质内,减少传输途中的能量损耗。其中在海水中传输损耗的能量较小,主要是因为海水中还有的杂质较少,并且短波沿经的路线会发生漫反射,这样便会将原有路线中的短波能量集中至一个层面上。
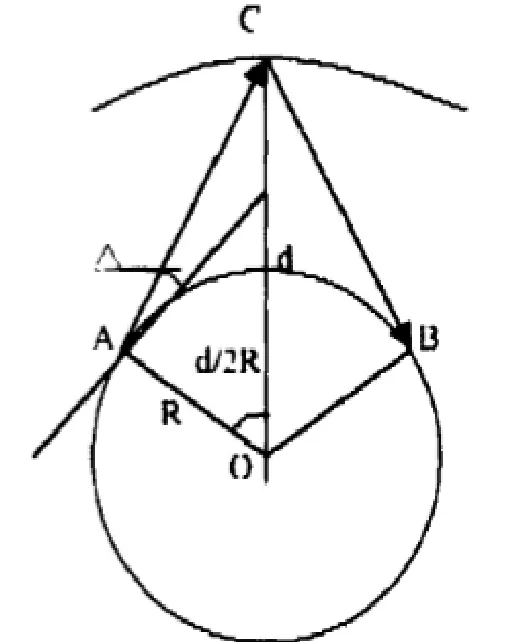
图1 天波传输路径模型
但在地面介质传输的损耗便会较大,主要是因为地面地势的起伏,造成在沿经线路上会发生无线短波的散射,至此短波之间形成叠加和衰减,衰减区便会使两侧的短波信号减弱,造成无线短波传输线路的中断。此外地球曲率对短波的传输损耗也具有一定的影响,在判定短波传输损耗上要根据短波信号的类型以及传输功率来划分,并且也要根据辐射源与接收机之间的传输路径来分析短波传输损耗的多少。在公式:
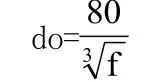
do表示在传输路程中的极限距离,f表示在短波信号辐射频率。当f=20MHz时,可得出短波的理想传输路程为74km。但由于外部介质密度的差异性,最终的传输距离在20公里左右,假设短波在传输过程中遇到较大的障碍物,则会使得传输的距离继续缩短。
1.2 天波传输损耗
天波传输损耗可分为四种模式,分别为:电离层短波传输损耗、短波反射损耗、空间能量扩散损耗以及附加损耗,可用的表达式为:N=N1+N2+N3+N4,在空间能量扩散损耗中主要受信号源的工作频段、短波的传输距离、地球半径以及射线的辐射角。在地球半径确定情况下,信号源的工作频段在10MHz时,射线的辐射角越大,使之达到电离层的距离缩短;射线的辐射角越小,使之达到电离层的距离便会延长;具体传播模式如图1所示,在电子负荷浓度较大的区域,辐射角度便会随着信号源工作频段的改变而改变,表达式中N1=20kdB,N2=13kdB,N3=22kdB,N2=18kdB,最终的传输损耗N=73kdB。
2.短波天线常见问题及解决措施
2.1 短波天线阵元的选取
在短波天线传输途径中,设计天线的阵元过短或者过长都会造成一定因素的影响。假设在设计天线短波阵元间距为高频段的半波长时,便能使得在传输过程中找到一定的方向性。但对于该频段的内的短波便会造成波长的差异性,减少原有波长的传输距离,此外在天线耦合方式上造成一定限度的耦合效应,使得短波在该频段失去对前方物质的扫描能力和判断能力。假设短波天线阵元的间距为低频段的半波长时,便会使得在低频段传输过程中会有较好的传输效果,但对于短波在高频段的传输路径中,便会加大波长的传输距离,使得传输的波长增加至原有的三倍。所以在选取短波天线阵元间距时,要根据天线的辐射角度和频段的选定范围来选取,这样便能在有限的传输路径中减少天线的传输功率。
2.2 短波天线外围因素的影响
短波天线外围因素的影响包括:天线的放置方式和架设施工的盲目性,其中在天线的放置过程中要根据地面的磁感线的强度来方式短波天线。主要是因为空间磁感线由N极指向S极过程中,会引发感应电流。便会与短波天线产生的感应电流相互叠加,造成磁感线的强度变大,使天线在传输路径中的阻抗以及方向发生变化,严重影响了短波天线信号的传输。在阻抗传输效应上也具有一定的影响因素,其中主要受馈线与无线电发射信机影响,当馈线与无线电发射机产生的阻抗一致时,便会获得较大的传输功率,这样能够在有效时间内保证传输数据信号的有效性。假设馈线产生的阻抗值为2000Ω,无线电发射机产生的阻抗值也为2000Ω时,在短波天线电压一定的情况下,根据公式:
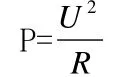
可得,传输的功率可得到最大值。在外界干扰因素中周围带有磁场的障碍物对短波天线信号的监测也具有一定的限制因素,其中短波天线在发射高功率信号时,遇到前方不明障碍物时,便会使传输的信号发生反射效应造成传输信号的中断。所以尽量假设短波天线时减少周围具有高层的建筑群体。
3.结语
通过对短波天线常见问题的分析,使之在现有层面上有了重新的规划,有效保证了短波天线传输数据信号的有效性。
[1]束咸荣.相控阵天线外监测系统电磁关系分析及优化设计[M].微波学报,2002,13(2):45-48.
[2]李迪,王华.中场测量相控阵扫描方向图的方法研究[M].现代雷达,2005,21(7):48-50.
[3]J.W.Brewer.Kronecker Products and Matrix Calculus in System Theory.IEEE Trans.on Circuits and Systems,2004,25(9):72-73.
[4]R.C.Hansen.Measurement Distance Effects on Low Sidelobe Patterns[J].IEEE Trans.on AP,2005,58(12):42-44.
[5]Y.Rockah,P.M.Schultheiss.Array Shape Calibration Using Sources in Unknown Locations-A Maximum Likelihood Approach[J].IEEE.Trans.on AP,2009,35(12):75-76.

