基于Matlab的电阻抗成像技术研究

张 丽

（南通农业职业技术学院 江苏 南通 226007）

电阻抗断层成像（EIT，Electrical Impedance Tomography）是一种新型的医疗成像技术。EIT可应用于肺功能检测，皮肤癌、乳腺癌预防检测，大脑活动成像等。EIT技术用于大脑活动检测主要有：脑缺血、脑出血、癫痫灶定位，正常脑功能分析及神经元活动的观察分析。

目前为止，电阻抗断层成像技术的绝大多数应用程序都被认为是实验性的，还处于研制阶段，然而，与目前广泛采用的X-CT技术相比具有很大的优越性。EIT技术是功能成像，可以准确的判定病变的性质种类，对人体无害，可以反复使用，实现了实时成像。由于生物体的功能性病变先于器质性病变，用EIT技术对生物体检测，可以起到对疾病的预防作用[1]。

1 EIT技术研究背景

生物组织的电导率和介电常数在不同组织中，相同组织不同温度下以及不同生理因素条件下均不同。例如，肺部充满气体时，导电性能减弱。

1978年，John G Webster首次将EIT技术运用于医学图像技术。1984年，David C. Barber和Brian H. Brown开发了第一个医用的EIT系统。Sheffield Mark 3.5是由Sheffield大学研究小组开发的第一个商业版本的EIT系统。2011年出现了第一个用于肺部检测的商业EIT设备。EIT系统中通过多路转换器进行电极转换的单个电流源和电压—电流转换器系统，均由数模转换器来控制。EIT系统可以直接进行信号的数字转换，解调，可以工作在不同频率下，可以同时测量电压的幅值和相位。EIT系统测量得到的电压数据传输到计算机进行处理，进行图像的重建和显示。

2 EIT技术工作原理

EIT技术通过对生物体表面的电测量得到生物体内部的电导率图像及生物体部分的介电常数。一般情况下，将电极施加粘稠剂后附着于皮肤表面，在全部电极或部分电极上注入有效值恒定（约几毫安）的微小低频交流电流（频率为10～100 kHz），测量生物体表面电势，可多次注入测量求平均值保证数据的准确性。根据生物体表面的电测量数据得到生物体内部电导率分布在数学上是一个非线性的逆问题，它是病态的[2]。逆问题的数学推导通常被称为“卡尔德隆问题”，人们在逆问题解的唯一性和数值算法方面有着大量的研究。

2.1 EIT技术控制方程

EIT技术本质上是在建立在一定假设基础上，施加了边界条件的电磁场问题。在低频条件下，将成像目标看作为离子导电体，并且不考虑测量电极的面积，成像目标可以视为准静态场域，它的电流密度、电导率、和电场强度满足下列关系式

电流连续性方程为

得到电场强度和电位之间的关系为

根据电磁场理论得到EIT技术的控制方程如下

其中，σ为生物体内部电导率，Ф为生物体体表电位。已知Ф求σ称为逆问题，它是在已知σ求解Ф的正问题基础上进行的，通常采用迭代的方法[3]。

2.2 EIT技术系统构成

EIT技术的系统构成包括：激励单元，测量单元，数据采集单元，软件实现单元[4]。为了保证生物体的安全，通常采用电流源激励的方式，电流源激励采用恒流源注入方式，电流强度大小可控，测量此时对应的边界电压，通过硬件设备（高精度的数据采集系统），将所得数据送往计算机，基于Matlab平台，根据一定的重建算法，编制程序，运行程序，得到生物体的电阻抗分布图像。

3 EIT技术重建算法

在EIT技术系统中重建算法的研究是软件实现的基础和保证。EIT的求解包括正问题和逆问题两部分。正问题一般采用有限元法求解。为了得到成像目标的绝对电阻抗分布图像，逆问题采用静态算法，兼顾收敛性能，收敛速度，成像效果等方面，通常采用修正的Newton- Raphson迭代算法[5]。

3.1 有限元剖分

假定连续求解域为圆形场域，场域的剖分方式有矩形、四边形、三角形、或曲边三角形等，这里采用三角单元剖分方式。

理论上，增加剖分单元或提高插值函数的阶次能够增加正问题求解精度，但也会严重影响到求解的速度，对逆问题的求解速度影响更大。场域的边界变化梯度大，为了得到较好的分辨率，对边界部分进行加密剖分。下图1为利用可被Matlab调用的有限元剖分软件QMG2.02得到的圆形场域剖分模型，剖分模型信息存放在有限元数据文件meshdata.dat中。场域半径为15，剖分单元为M=492个、节点N=279个。

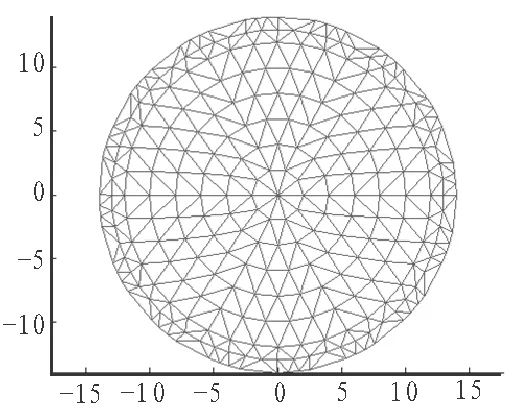
图1 有限元剖分图Fig. 1 Finite element mesh figure

3.2 测量电极及测量方式

测量电极的材料、形状、数量以及测量方式对EIT成像精度均有重要的影响。为使得测量位置准确，减小接触阻抗，兼顾测量精确性和数据处理的复杂性选用16个均匀放置的圆形点电极来测量。测量方式选用相邻或相对的方式，独立测量次数分别为N (N -3)/2，N (N -4)/2，其中N =16[6]。

3.3 修正的Newton-Raphson迭代算法

设定真实的电阻率分布为ρ*，注入电流，测量相邻电极上电压为Uij，根据Uij求解ρ*就是EIT逆问题。由于有限元求解方法中人为的认定每个剖分单元电阻率恒定，而实物电阻率可能是处处不等的，同时，由于测量误差的存在，一般情况下寻找的是电阻率分布ρ。已知电阻率分布ρ，利用有限元法计算得到的相邻电极上的电压Vij(ρ)，此时，Vij(ρ)与Uij之差最小，即下式（5）的E(ρ)最小，它是数学上的最小二乘问题。

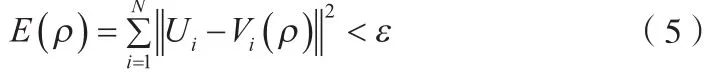
EIT中，Jacobi矩阵反映了每个单元电导率变化对边界电位的影响，由于Jacobi矩阵广义逆的条件数很大，使得逆问题存在严重的病态性，引起解的不适定，正则化的方法可以解决这个问题。Tikhonov正则化通过罚函数来实现对解的阻尼作用，克服了EIT逆问题的病态性，得到修正的Newton-Raphson迭代算法[7]。如下式所示。

其中，α为正则化因子，L为正则化矩阵。

3.4 逆问题求解算法程序

下面给出用matlab编制的逆问题算法程序。

A=UpdateFemMatrix(Agrad,Kb,M,S,ones(NElement2,1)); //更新有限元矩阵，得到系统矩阵

Uref=ForwardSolution(NNode2,NElement2,A,C,T,[],'real',p,r);//正问题求解

rho0=Uref.Electrode(:)U.Electrode(:);

rho=rho0*ones(size(sigma)); //设定电阻率初值

A=UpdateFemMatrix(Agrad,Kb,M,S,1./rho); // 根据变化的电阻率. 更新有限元矩阵，得到系统矩阵

Uref=ForwardSolution(NNode2,NElement2,A,C,T,[],'real',p,r);//正问题求解

Urefel=Uref.Electrode(:);

J=Jacobian(Node1,Element1,Agrad,Uref.Current,Uref.MeasField,rho,'real'); //生成Jacobi矩阵

alpha=0.000005; //正则化因子

R=MakeRegmatrix(Element); //正则化矩阵

iter=5; //迭代次数

for ii=1:iter

rho=rho+(J'*J+alpha*R'*R)(J'*(Uel-Urefel)-alpha*R'*R*rho);//修正的Newton

-Raphson算法

A=UpdateFemMatrix(Agrad,Kb,M,S,1./rho);

Uref=ForwardSolution(NNode2,NElement2,A,C,T,[],'real',p,r);

Urefel=Uref.Electrode(:);

J=Jacobian(Node1,Element1,Agrad,Uref.Current,Uref.MeasField,rho,'real');

clf,Plotinvsol(rho,g1,H1);drawnow; //迭代求解，绘制图像

end

4 二维EIT技术的matlab仿真

实际生物体是三维的，为了简化问题的分析，在二维场域内进行仿真成像，三维技术也是在二维问题研究的基础上推进的。

4.1 单个及几个成像目标

如图2所示，有限元模型中，绿色部分电阻率设定为0.005，其余部分电阻率为0.002 5，运用上述的正、逆问题成像算法，分别得到图（a）一个，图（b）两个，图（c）3个成像目标的matlab仿真图像，图像中的灰度变化反应了电阻率大小的变化。

4.2 算法参数对成像效果的作用

如下图3所示，对kupio系统的人体实测数据进行图像仿真，观察正则化因子和迭代次数对成像效果的影响。

图2 单个及几个目标成像图Fig. 2 Single and several imaging target reconstrucion tomography

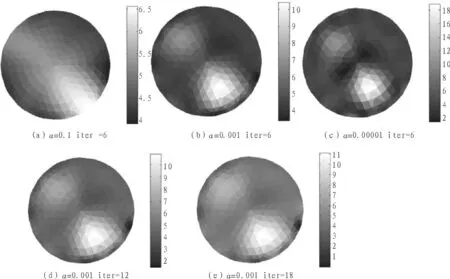
图3 kupio系统数据成像图Fig. 3 Kupio system data reconstrucion tomography

减小正则化因子 ，可以明显改善成像效果。增加迭代次数，成像效果改善不明显，成像速度变慢。

4.3 实测数据的成像对比分析

将电极1放置于人的前额，对人的双耳施加计算机发出的有规律的75 dB刺激信号，采用16电极对相测量方式，施加有效值为1 mA的交流电流，每间隔300 ms进行数据采集，得到256个测量边界的电压数据（硬件测量数据由英国曼彻斯特大学提供），对124组数据进行处理，去除16组刚开始测量波动较大的数据，将未施加听觉刺激的数据与听觉刺激后得到的数据生成.dat文件，供matlab 程序调用，得到听觉刺激前后的matlab仿真图像，如图4所示。

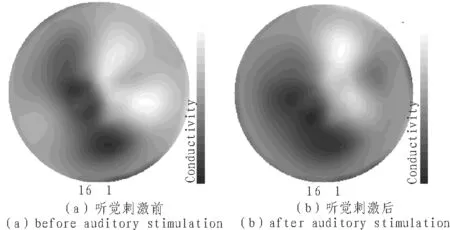
图4 人脑电阻抗成像图Fig. 4 Human brain electrical impedance tomography

人的大脑白质电阻率为6.8，大脑灰质电阻率为2.8，脑髓液电阻率为0.65。图4中颜色较深处电阻率较大，较浅处电阻率较小。听觉刺激后颜色普遍加深，电阻率主要呈增大趋势。

5 结束语

电阻抗断层成像技术具有无辐射、无损伤，功能性成像的特点，可实现实时成像，正在受到人们的广泛关注[8]。现在全球地震多发，大型的检测仪器无法实时实地的进行救护检测，而EIT技术的成功应用能有效地应对这些危急的情形。

目前，大量的EIT技术研究局限于二维问题，而实际生物体是三维的，因此，在二维的基础上更多的进行三维EIT的研究将有助于尽快的使该技术趋于成熟，真正的服务于医疗领域[9]。

[1]何为, 罗辞勇，徐征,等.电阻抗成像原理[M].北京:科学出版社.2009.

[2]杨硕.电阻抗断层成像技术综述[J].河北工业大学学报,2004,33(2):35-39.YANG shuo.Electrical impedance tomography review[J].Hebei University of Technology Journal,2004,33(2):35-39.

[3]KimHwaLim,GuiningShi,KyleMc Carter,Rhett George Jr,et al Design meeasurement,simulatio,and imagerecon struction,microwave and optical technology letters[J].Deit For Biomedicallma ging,2007,49(12):2989-2998.

[4]石小累.应用于肺通气功能成像的EIT系统设计及实验研究[D].天津:天津大学,2008.

[5]徐管鑫.电阻抗成像技术理论及应用技术研究[D].重庆:重庆大学,2004.

[6]王化祥,王超.陈磊.EIT系统复合电极结构性能分析及优化设计[J].仪器仪表学报,2002,23(2):189-191.WANG Hua-xiang,WANG Chao,CHEN Lei.Composite electrode performance analysis and optimization for EIT system[J].Chinese Journal of Scientific Instrument,2002,23(2):189-191.

[7]王戳.电阻抗成像算法的研究[D].山东:山东大学,2006.

[8]Boone K.Imaging with eleetricity:Review of the European Concerted Action on Impedance Tomography[J].Journal of Medical Eng&Tee hnology,1997,21(6):201-232.

[9]Holder. D. S. Electrical Impedance Tomography: Methods, History and Application[C].Institute of Physics Press, London (2005).