数学实验与数学建模研究的程序基础

卢振坤，叶海燕

（1.广西民族大学 信息科学与工程学院，广西 南宁530006；2.梧州学院 文法学院，广西 梧州543002）

进入21 世纪，高等教育必须把培养高素质创新型人才作为根本目标。而数学作为一门基础学科，已经渗透到各个领域，并越来越深刻地影响到相关学科的发展。数学建模与数学实验是与解决实际问题联系紧密的课程，如今各个高校都开设了该课程，而且有关如何进行数学建模与数学实验的课程改革以及如何把数学建模思想渗透到平时的数学课中等问题已经有很多文献进行探讨[1—8]。文章主要针对数学建模与数学实验研究程序，从数学的角度进行分析，给出一个量化的实现过程。

现实中，研究对象往往是复杂而且是随机的。在数学建模与数学实验中，我们可以在定性的和定量的程度上进行实验。在定性实验中，往往只得到研究对象的某一特征，其测量精度是未知的，其目的是研究对象的具体性质。而定量实验则不同，是用模型的方法获得研究对象的特征，可进行一定的误差控制，主要目的是要精确测定我们所关心的特征。实验中要完成的主要任务是：

（1）积累有关研究对象已知性质的信息；

（2）探索研究对象的新性质；

（3）检验建立的理论模型的正确性；

（4）求解反概率问题。

1 定量实验研究及概率特征的鉴别泛函

当利用定量方法去研究某个对象时，我们要用一些函数去描述研究对象的性质，比如随机过程x(t)就是这种函数理想化的模型。根据先验信息a 和我们采用的假设h 来建立假设对象，相应的模型可表示为：

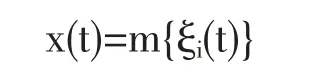
其中m=(a,h)是一个算子，它表示根据先验信息a 和假设h 所选择的模型的类型；ξi(t)，i=1,2,…，p 是随机过程，假设它的概率特征是已知的。模型m∈M 必须形成集合M，并足以完整地描述实际研究对象的性质。

设θ(l|m)是与x(t)的模型m 相对应的随机过程x(t)的概率特征，这里l=(l1，l2，…，ln)是研究过程中作为概率特征的自变量出现的独立变量的集合（n 决定它的维数）。从它依赖于模型m 的观点看，概率特征θ(l|m)是有条件的。若令πi(λ),i=1,2,…,p 为随机过程ξi(t)的概率特征，λ=(λ1，λ2，…，λp)为对应的独立变量的集合。根据定义，概率模型必须使我们能够建立原始的概率特征{πi(λ)}和θ(l|m)之间的联系，即

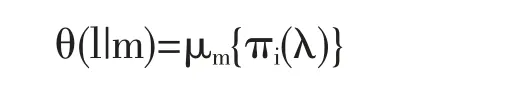
这里μm唯一地由算子m 所确定——即由随机过程的模型所确定。

在定量的实验中，我们必须求出概率特征θ(l|m)和这个特征的统计估值之间(l)数值的对应关系。实际上，不求出这一对应关系，我们就不能得到一个定量的实验结果。

对于所研究的特征我们引入鉴别泛函ρθ(m)：

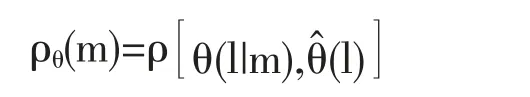
这里ρ 表示一个运算形式的算子，用这种运算形式来确定θ(l|m)和(l)之间的差别。

因此，ρθ(m)是一个数，这个数在某种意义上确定在由它们的自变量所描述的空间函数θ (l|m)和(l)之间的距离。

引入鉴别泛函使我们能够确定统计测量的误差，并能用数值估计的定量形式表示出试验的结果。

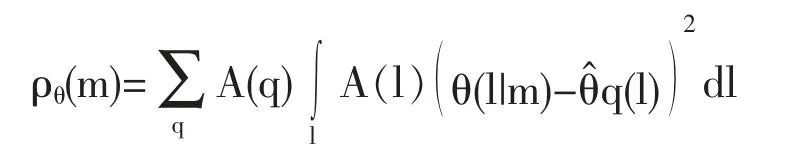
其中A(q)和A（l）是相应的权函数。

2 研究基本模型

鉴于对研究对象性质的假设以不同的充分程度反映研究对象真实的性质，自然我们假定对于不同的模型m∈M 泛函ρθ(m)的值将会不同。在模型的集合中存在一个最小的泛函ρθ(m)。

把m0∈M 定义为基本模型，它对应于泛函ρθ(m)的最小值，即

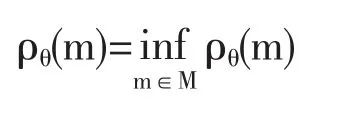
其中表示下确界。

显然对一个具体的模型m，ρθ(m)的值越接近ρθ(m0)的值，则这个模型就越准确、越有效。某一个模型有效度E(m)的定量测度可以定义为：

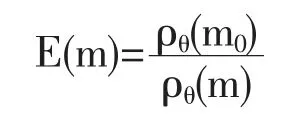
模型m 的有效度E(m)有下面的性质：

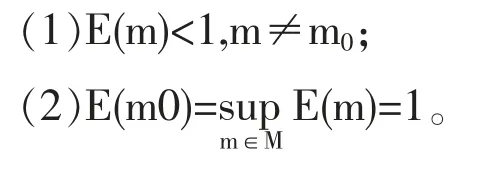
其中sup 表示上确界。

在建立模型M 集合的过程中我们必须考虑所有可利用的先验信息a，此外我们还必须考虑与研究对象可能的特性有关的假设h。在一般情况下，任何两个模型mi和mj可以利用所考虑的形成的先验信息量ai和aj，以及在确定这些模型时所作的假设hi和hj来加以区别。对于绝大多数有实际意义的情况，我们可以假设用来建立不同模型的先验信息量是相等的，即ai=aj=a，而模型mi=(a,hi)和mj=(a,hj)的差别仅仅表现在所采用的假设hi和hj的性质方面。但是即使不是这样，严格地讲，所考虑的先验信息量的不同原则上与对应假设的特征有关。这样，在这种解释中模型的差别来自所作的假设的差别。如果我们用H 表示可能的假设h∈H 的集合,显然，集合M 唯一地被集合H 所确定。

3 试验模型结果的解释

试验研究的一个重要的阶段是试验结果的解释，它定义为对实际研究对象的性质进行判决的一个步骤，其目的是控制后来的试验和导出使用所得的数据的推荐值。

采用的模型m 与实际对象的模型完全相匹配，用Δρθ(m)表示对应于这种情况的泛函ρθ(m)的值，显然这样一种情况是假定的，但尽管如此，从方法论的观点出发还是值得研究的。考虑到以上的讨论，看出在统计测量中Δρθ(m)的值应当作为算法误差和设备的误差来对待。

假定与第m 个模型相对应的概率特征θ(l|m)是研究对象的真实特征，则可以计算Δρθ(m)的值。自然希望对于基本模型m0来说Δρθ(m)是最小，也就是

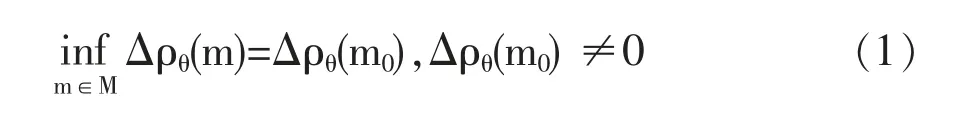
以下述方法证实上式的正确性。统计测量的误差（至少是算法误差）取决于所采用的模型与实际研究对象一致的程度。在这种情况下，一致程度越高——也就是所研究的模型m 与基本模型m0越接近，这些误差就越小。按照基本模型(m)的定义，它是在所有m∈M 中与真实模型最接近的。于是式（1）的正确性得到证明。

令ε 为一正数，则值

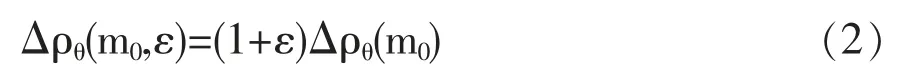
相当于最小统计测量误差乘以(1+ε)。当然ε具体值的选择必须合理，并要考虑到要解决的问题的特殊性质和利用实验数据的特殊性质。ε 值起的作用是规定一个确定的置信范围用以确定对于泛函ρθ(m)的容许值的限制。

如果作为一个实验结果满足条件

则选择基本模型m0的任务便完成，试验也就结束。将来，在不等式（2）所确定的这组条件下模型m0可以用来预测研究对象的性质。

但是，如果得出

则就不能认为得出的基本模型足以表示实际研究对象（当然对于假定的ε 值）。在这种情况下，可能的模型集合M 必须由另一个模型集合M1来代替，使得

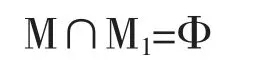
其中Φ 表示空集。

进一步的研究变为在模型m1∈M1中寻求基本模型m10。如果得出

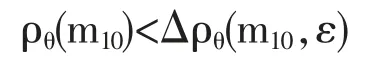
则试验就结束。但是，如果

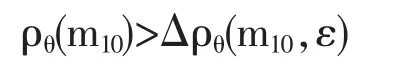
则必须依次引入模型的集合MR，R=2,3…，使得

并寻求基本模型mR0，直到对某个mR0不等式

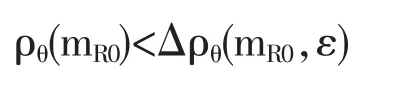
成立为止。

其次，研究形成的概率模型的集合MR(R≥1)的一些特性，在模型集合M 的讨论中曾把先验信息a 和假设h∈H 用作原始数据。

如果考虑式（4）成立，有必要引入模型集合MR，MR的形成一方面用新的假设HR；另一方面用附加的先验信息a+ΔaR，在这种情况下，信息ΔaR由试验研究的下一个周期得到。

4 结 论

数学实验与数学建模的改革是深化高校数学教学改革，全面提高教学质量，培养二十一世纪创新型高素质人才的有效途径。而数学建模不能只是停留在感性认识上，否则面对实际问题时就无法找到切入点，无法建立合理的数学模型，更不能对结果做出合理的分析。文章从数学的角度进行分析，给出一个量化的实现过程，让学生对整个数学建模和数学实验的过程有一个理性的认识，从而更好地指导他们解决实际问题的能力。

[1] 孙莱样.积极探索创新人才培养模式[J].中国高等教育,1999(24):10-11.

[2] 姜启源.数学实验与数学建模[J].数学的实践与认识,2001(31):613-17.

[3] 李大潜.将数学建模思想融入数学类主干课程[J].中国大学教学,2006(1):9-11.

[4] 郑煜.数学建模:创新一体化教学模式的构建[J].黑龙江高教研究,2008(8): 177-179.

[5] 王庚.数学建模与数学实验课程的探索、实践与收获[J].高等数学研究,2007(1):101—102.

[6] 楼建华.数学建模与数学实验[J].黑龙江高教研究,2003(3):126-27.

[7] 陈华友.重视数学建模提高学生综合素质的作用[J].中国教育报,2008(9): 1-2.