用于光伏系统的一种最大功率跟踪方法

李晨霞 杨洪耕 王元驰

（1. 四川大学电气信息学院，成都 610065；2. 四川省电力公司乐山供电公司，四川 乐山 614000）

用于光伏系统的一种最大功率跟踪方法

李晨霞1杨洪耕1王元驰2

（1. 四川大学电气信息学院，成都 610065；2. 四川省电力公司乐山供电公司，四川 乐山 614000）

光伏电池的最大功率点跟踪可以显著提高光伏电池的转化效率。提出一种快速、稳定的最大功率点跟踪方法。根据最大功率点功率对该点电压的微分为0，推导出最大功率点功率Pmax与最大功率点电压Umax的关系方程，称之为最大功率曲线方程。最大功率曲线与光伏电池固有的功率-电压（P-U）曲线的交点即是最大功率点。以当前工作点为起点，以自动变步长在P-U平面上搜索出该交点即跟踪到最大功率点。仿真结果表明该方法能快速、精确地跟踪到光伏电池的最大功率点，且消除了最大功率点处的振荡现象，提高了系统的稳定性。

光伏电池；最大功率点跟踪；最大功率曲线

太阳能因丰富、清洁、无污染、无噪声等优点成为一种重要的可再生能源，并且得到了国家的一系列政策的扶持。但由于太阳能发电一次投资成本较高，且转化效率较低，近年来研究者主要致力于提高光伏系统转化效率、降低成本的研究。光伏电池具有很强的非线性特征，受光照和温度影响大，且在某一光照和温度下只有一个最大功率点（Maximum Power Point，简称MPP）。提高光伏发电系统整体转化效率的一个重要途径是实时调整光伏电池的工作点，使之始终工作在最大功率点附近，这一过程就称之为最大功率点跟踪（Maximum Power Point Tracking，MPPT）[1]。

基本的最大功率跟踪方法包括恒压法、扰动观察法[1-3]、电导增量法[4-5]等。扰动观察法、电导增量法都存在步长选择的困难，步长的大小将决定最大功率点的跟踪速度。步长较小时太阳能电池板很可能长时间工作于低功率输出区，步长较大时最大功率点附近的振荡加大。快速跟踪并稳定运行在最大功率点一直是各种方法努力追求的目标。文献[6-8]分别采用变步长方式对固定步长的扰动法和电导增量法进行改进，在一定程度上提高了跟踪速度，但在最大功率点处仍存在振荡现象。文献[9]提出了基于最大功率点的实验分析结果和太阳能电池的P-I输出曲线的交点作为最大功率点，这种方法的速度快，但是求解相关的数学代数式很复杂。文献[10]通过把输出功率曲线划分成两个区域，在不同的区域分别采用不同的控制方法使输出电流快速接近或达到最大功率点时的工作电流。但是这种方法需要同时采样开路电压和短路电流，而且在区域Ⅱ又采用部分开短电流估算最大功率点时的电流，根据此电流判断调节的电流步长。多次估算既降低了跟踪精度也使跟踪方法变得错综复杂。文献[11]提出一种快速的最大功率点跟踪方法。首先通过实验数据分析，得出不同光照下的最大功率点近似在光伏电池功率-电流（P-I）关系平面上的一条直线上，并以该直线将实际的 P-I特性曲线分为两个区域。在区域Ⅰ和区域Ⅱ分别采用不同的变步长法进行最大功率点跟踪，避免了最大功率点附近的功率振荡。但是区域Ⅰ的跟踪步长较小，跟踪速度较慢；在区域Ⅱ控制中需要实时测量短路电流，使得系统不能稳定的对外输出能量。

本文首先根据光伏电池最大功率点功率对电压的微分为0的特征，推导出最大功率曲线方程。根据方程在功率-电压关系平面上绘制出最大功率曲线，该曲线与光伏电池固有功率-电压（P-U）曲线存在唯一的交点，该交点就是最大功率点。以当前工作电压与最大功率曲线上同功率点对应的电压之差为步长，搜索出该交点即跟踪到最大功率点。该方法在最大功率点附近不存在振荡问题。仿真证明该方法能够快速精确的跟踪到最大功率点，提高了光伏电池的转化效率。

1 光伏电池的特性

太阳能电池阵列的输出电压U和输出电流I的关系[12-14]为式（1）。

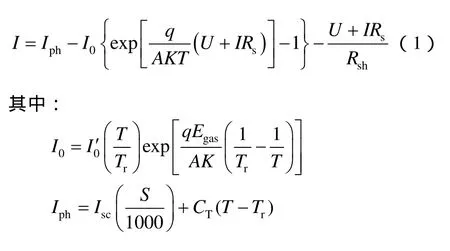
其中：Iph为光生电流；I0为 PN结反向饱和电流；q为电子的电荷量；A为PN结的曲线常数；Rs为串联电阻；Rsh并联电阻；k为Boltzmann常数；T为电池表面温度；Tr为参考温度；CT为温度系数，CT=1.6×10-3A/K；S为光照强度；Egas为禁带宽度。

对于理想的光伏电池，Rs很小，而 Rsh很大。光伏电池的输出电压U和输出电流I关系等效为：

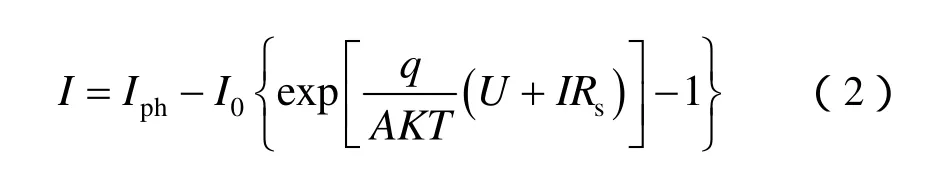
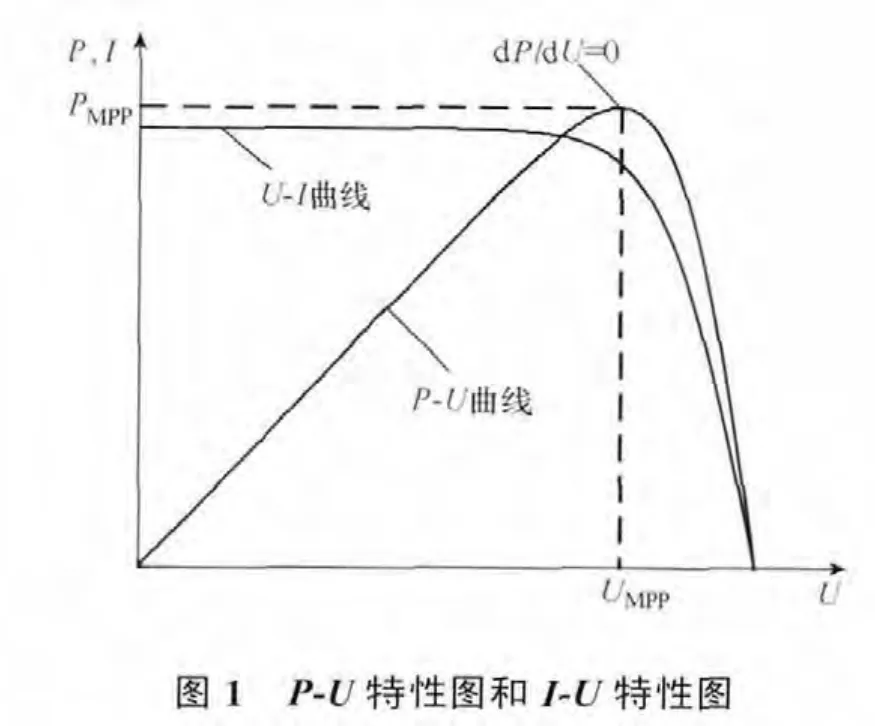
图1是光伏电池在标准光照和标准温度条件下的P-U特性和I-U特性。可以看出，光伏电池的伏安曲线是非线性的，并且在一定的温度和光照条件下有唯一的最大功率点。为了提高光伏电池的发电效率，应该让光伏电池工作在这一点上。但是光伏电池最大功率点的电压随光照和温度的变化而变化，因此常在负载和光伏阵列之间加入最大功率跟踪控制器，使光伏阵列工作在最大功率点上。

2 最大功率曲线

在温度和光照强度确定的情况下，光伏电池具有一条特定的功率-电压曲线（P-U曲线），且仅有一个最大功率点。当温度恒定，光照强度不断变化时，形成一簇功率-电压曲线（P-U曲线），且每条曲线都有一个最大功率点。将这些曲线上的最大功率点连接起来形成一条曲线，该曲线称之为光伏电池的最大功率曲线，如图2（a）所示。最大功率点就是光伏电池的P-U曲线和最大功率曲线的交点。从图2（a）中可以看出在温度恒定的情况下，最大功率点随着光照强度的变化而变化，但是最大功率曲线是固定不变的。

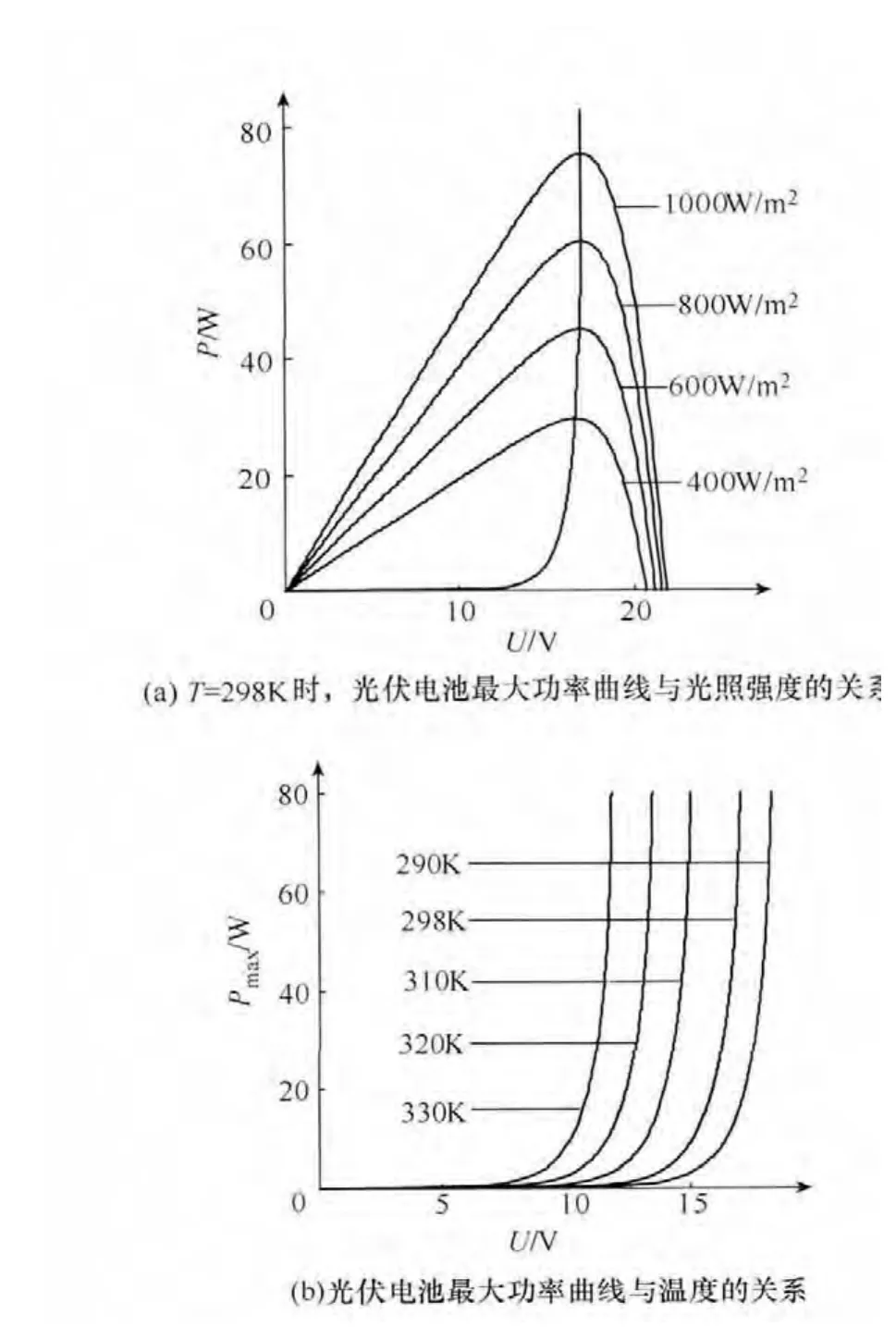
图2 最大功率曲线

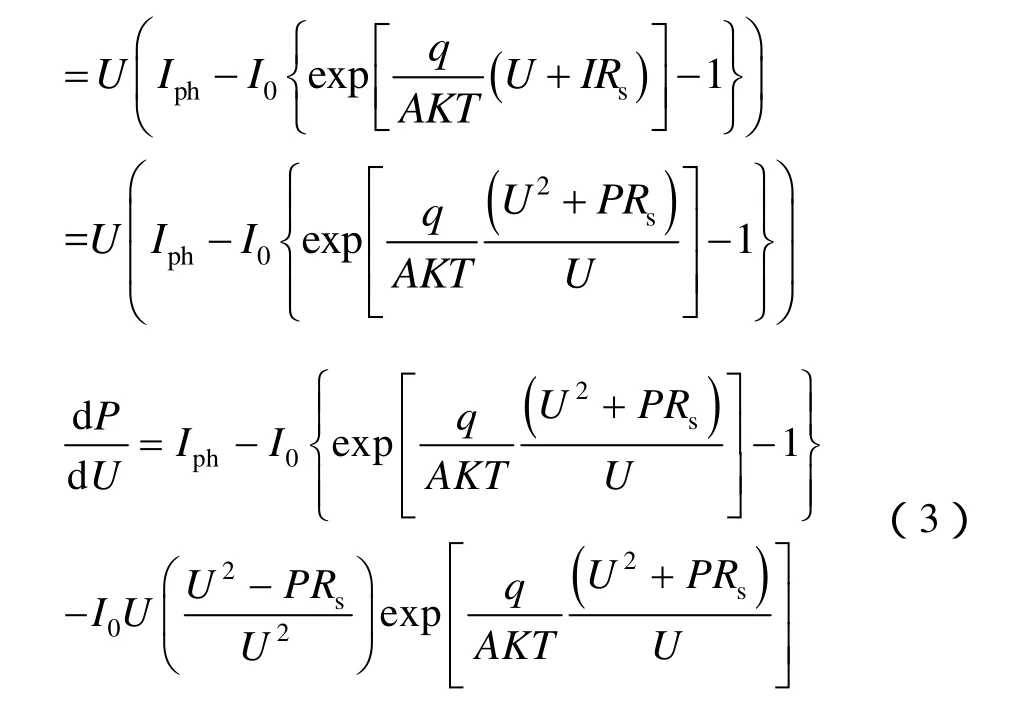
当光伏电池工作在最大功率点时，最大功率和对应电压的关系为：dP/dU=0。

将最大功率点功率和电压分别用 PMPP和 UMPP表示并化简上式则可以得出以下关系：

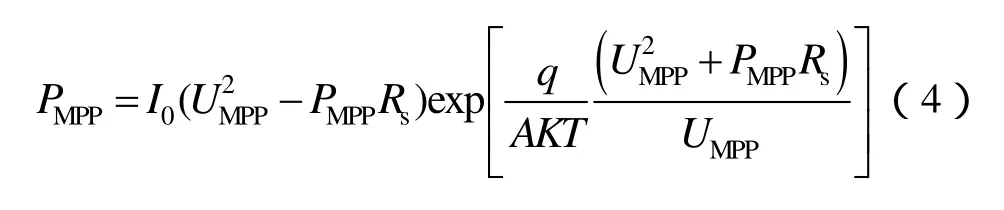
式（4）是光伏电池的最大功率曲线方程。在式（4）中，只有I0和T是变量，其他都是与材料有关的常数。而I0只与温度T有关，不随光照变化而变化。最大功率曲线随温度变化的关系如图2（b）所示，当温度升高时，最大功率曲线向左偏移。

3 最大功率点跟踪

由上一节分析可知，最大功率点是光伏功率曲线与最大功率曲线的交点。在图4中，P0为最大功率点。曲线1是光伏电池的功率-电压特性曲线（P-V曲线），曲线2是光伏电池的最大功率曲线。以下为寻找最大功率点的步骤：

第一步：置k=1。

第二步：光伏电池初始状态运行在Ak（Uk，Pk）。

第三步：在最大功率曲线2上找到与Ak点同功率的Bk（Uk+1，Pk）。其中Uk+1由公式（4）求出。

第四步：以Uk+1为运行电压，得到P-V曲线上对应的 Ak+1（Uk+1，Pk+1）。

第五步：求Pk+1与Pk的差值。

如果差值大于设定误差，则 k=k+1，转至第二步，进行下一次搜索。

如果差值小于设定误差，则Ak+1（Uk+1，Pk+1）就是光伏电池的最大功率点。

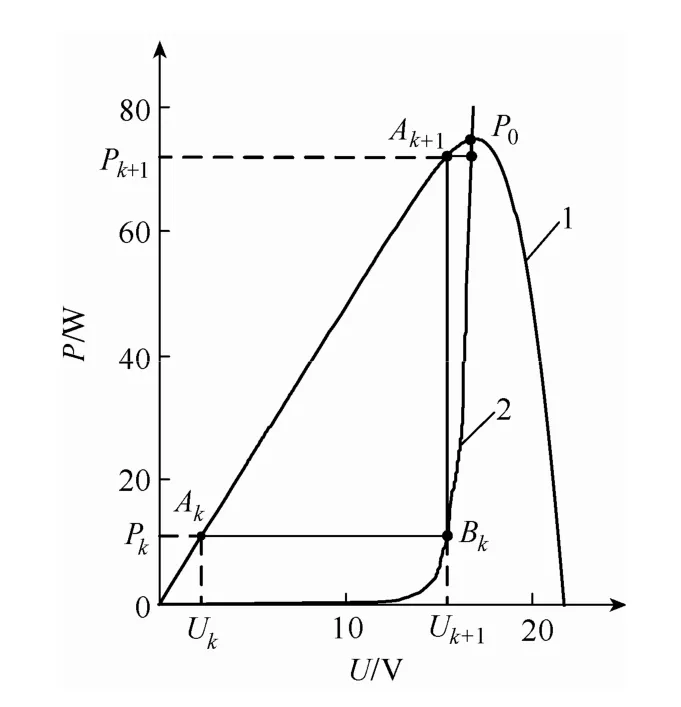
图3 最大功率点跟踪

通过以上跟踪过程可以看出：在跟踪初期，因最大功率曲线比较平缓，因此搜索的步长较长。经过两到三次搜索即达到最大功率点附近，极大的提高了跟踪速度。而在最大功率点附近，最大功率曲线比较陡峭，搜搜步长较短，从而提高了跟踪精度。因此，基于最大功率曲线的最大功率点跟踪方法无论在速度还是精度上都较其他方法有明显的提高。跟踪过程中无需测量光照，只要测量温度以及当前工作电压和功率就可以跟踪到最大功率点。

公式（4）没有解析解，必须采用数值计算求解，计算量非常大，在实际应用中不方便。在图4中可以看出：最大功率曲线在电压较低时的取值并不影响最大功率跟踪，而在电压较高时，电压与功率呈现出近似线性的关系，所以可以用一条直线代替最大功率曲线。如图4所示，曲线1为标准环境下的最大功率曲线，在电压较高时，曲线1与直线2非常接近，因此可以用直线2代替曲线1。直线2由以下两点确定：

1）取光伏电池在标准环境下的最大功率点（Um，Pm）为第一点。

2）取光伏电池在标准环境下的最大功率的一半（Ux，Pm/2）为第二点，其中 Ux根据公式（4）计算得出。

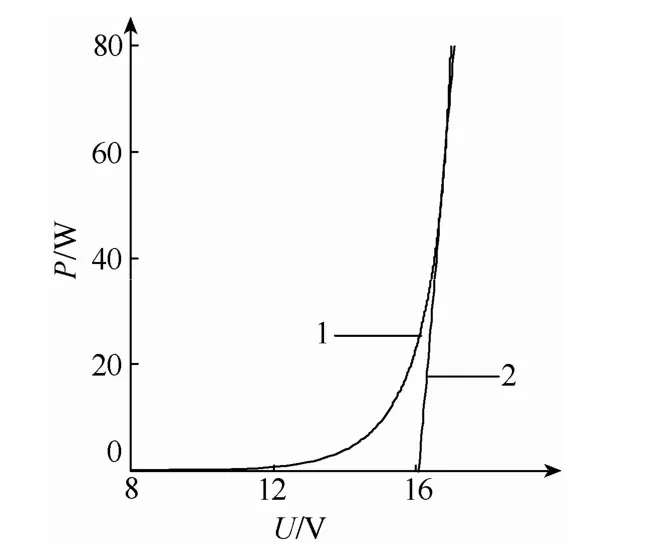
图4 最大功率曲线的近似

以德国Siemens公司的型号SP75光伏电池模组[15]为例，最大功率点处的电流Im=4.4A、电压Vm=17V和功率 Pm=ImVm=74.8W；在 Pm/2（37.4W）与 Pm（74.8W）之间，最大功率曲线1与直线2之间的最大误差不超过0.5%。

由图2（b）可以看出，随着温度的升高，最大功率曲线向左移动。表1为不同温度的最大功率曲线上，各同功率点的电压值（单位为V）。根据数据计算得出，在功率不变的情况下，温度每升高1K，电压降低约0.158V。以直线代替最大功率曲线后，在最大功率跟踪时，根据实时的温度，将直线向左、右移动就可以代替当前温度下的最大功率曲线。

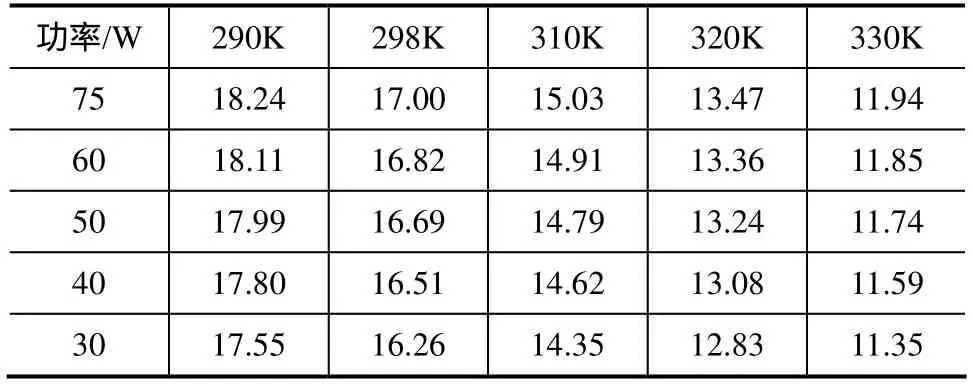
表1 不同温度的最大功率曲线上，各同功率点的电压值

采用直线代替最大功率曲线后，计算量显著减少，提高了跟踪速度。

4 仿真实验

为了验证基于最大功率曲线的MPPT法的有效性，本文采用Matlab建立了光伏最大功率跟踪系统仿真模型，并对基于最大功率曲线的MPPT法和文献[11]所采用方法的仿真结果进行了比较。

图5（a）、（b）分别为文献[11]所采用方法和最大功率曲线MPPT法在标准条件下进行最大功率跟踪的仿真结果。从图中可以看出，在跟踪程序起动后，电压很快从0上升至17V，电流从4.8A下降至4.4A。从初始状态到最大功率点，文献[11]的方法用时约0.02s，而最大功率曲线法在0.005s即达到最大功率点。最大功率曲线法运用在大型光伏发电中，可以提高光伏电池的转换效率。

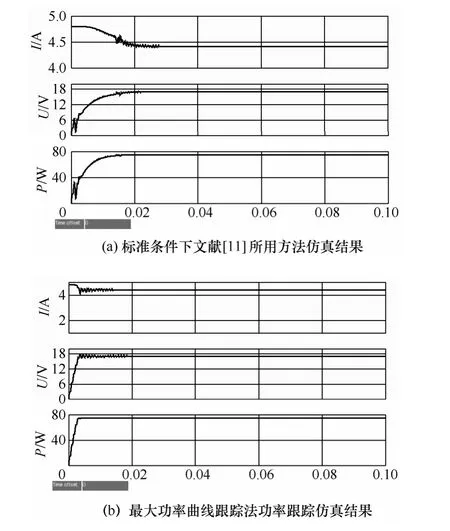
图5 标准条件下两种最大功率跟踪方法仿真结果比较

图6（a）、（b）分别为文献[11]所采用方法和最大功率曲线MPPT法在光照变化时的仿真结果。初始条件为温度 298K，光照为 1000W/m2。在 0.05s时，光照降低为400W/m2，从图中可以看出，文献[11]所用方法在约 0.015s后达到新的最大功率点，而最大功率曲线法则在0.008s后达到最大功率点。在寻找最大功率点时，文献[11]会有 37.5%的超调量，但是在最大功率曲线法中就只有 4.19%的超调量。明显可以看出，在光照变化时最大功率曲线法可以跟快的追踪到最大功率点，并且具有较小的超调量。

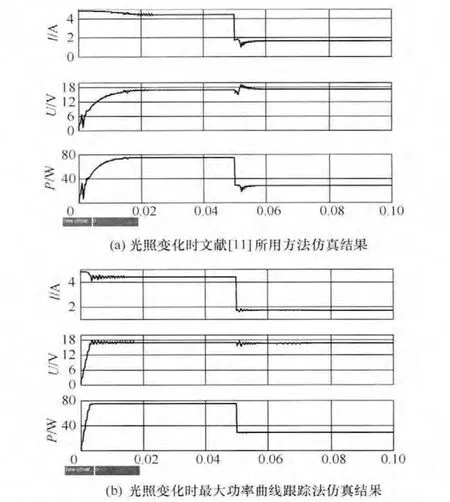
图6 光照变化时两种最大功率跟踪方法仿真结果比较

图7（a）、（b）分别为文献[11]所采用方法和最大功率曲线MPPT 法在温度变化时的仿真结果。初始条件为温度 298K，光照为 1000W/m2。在 0.05s时，温度增高为330K，从图中可以看出，考虑了温度影响的最大功率曲线MPPT法达到的精度比文献[11]所采用方法达到的精度高。在这组仿真中，0.05s时温度增加为330K，而文献[11]的方法并没有跟踪到正确的电流值，而是一个电流很低的点，此时电流为 1.30A，电压为 14.7V，所以功率 P=IU=1.3×14.7=19.11W，很明显这种方法在跟踪到P-I曲线中最大功率点右边的一个点就停止了跟踪，并没有跟踪到最大功率点。而在图（b）中，在0.05s后，电流为4.17A（与温度变化之前的电流变化不大），电压为 11.71V，功率 P=IU=4.17×11.71=48.83W。明显可以看出，在温度变化时最大功率曲线法可以更准确地追踪到最大功率点。

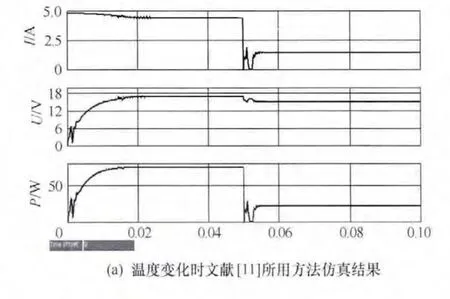
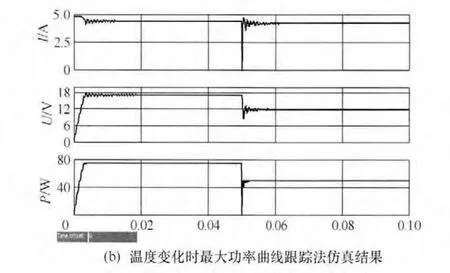
图7 温度变化时两种最大功率跟踪方法仿真结果比较

5 结论

本文提出的基于最大功率曲线（P-V）的最大功率跟踪方法，这种跟踪方法可以快速的跟踪到最大功率点，计算简单，不存在传统跟踪方法的步长选择困难，且有效克服了传统跟踪方法在最大功率点附近的功率振荡问题。通过仿真证明，无论是从初始状态开始还是在光照或温度突然变化的情况下，本文方法均能够快速、精确地跟踪到最大功率点，且在最大功率点处无功率振荡现象，稳态精度高，提高了光伏系统的转化效率。

[1] 何人望，邱万英，吴迅，等.基于 PSIM 的新型扰动观察法的MPPT仿真研究[J]. 电力系统保护与控制,2012, 40(7): 56-59.

[2] KJAER S B. Evaluation of the “Hill Climbing” and the“Incremental Conductance” maximum power point trackers for photovoltaic power systems[J]. IEEE Transactions on Energy Conversion, 2012, 27(4):922-929.

[3] 张小莲, 李群, 殷明慧, 等. 一种引入停止机制的改进爬山算法[J]. 中国电机工程学报, 2012, 32(14):128-134.

[4] 董密, 杨建, 彭可, 等. 光伏系统的零均值电导增量最大功率点跟踪控制[J]. 中国电机工程学报, 2010,30(21): 48-53.

[5] HSIEH G C, HSIEH H I, TSAI C Y, et al.Photovoltaic Power-Increment-Aided Incremental-Conductance MPPT with two-phased tracking[J]. IEEE Transactions on Power Electronics, 2013, 28(6):2895-2911.

[6] 王义飞. 吴伟, 张皞华, 等. 改进型变步长光伏最大功率点快速跟踪[J]. 上海大学学报（自然科学版）2011, 17(3): 249-252.

[7] 原敬磊, 张建成. 一种改进的变步长电导增量光伏电源 MPPT控制方法[J]. 电网与清洁能源, 2012,28(1): 75-79.

[8] 赖东升, 杨苹. 一种应用于光伏发电 MPPT的变步长电导增量法[J]. 电力电子技术, 2012, 46(3): 40-42.

[9] PAN C T, CHEN J Y, CHU C P, et al. A fast maximum power point tracker for photovoltaic power systems[C].Industrial Electronics Society, 1999. IECON '99Proceedings The 25th Annual Conference of the IEEE,1999: 390-393.

[10] MUTOH N, OHNO M, INOUE T. A method for MPPT control while searching for parameters corresponding to weather conditions for PV generation systems[J].IEEE Transactions on Industrial Application, 2006,53(4): 1055-1065.

[11] 高志强, 王建赜, 纪延超, 等. 一种快速的光伏最大功率点跟踪方法[J]. 电力系统保护与控制, 2012,40(8): 105-109.

[12] 邱培春, 葛宝明, 毕大强. 基于扰动观察和二次插值的光伏发电最大功率跟踪控制[J]. 电力系统保护与控制, 2011,39(4): 62-67.

[13] 赵云凤, 李田泽, 陈世宝, 等. 光伏发电非线性步长最大功率跟踪研究[J]. 可再生能源, 2013, 31(1):17-20.

[14] 赵争鸣, 刘建政, 孙晓瑛, 等. 太阳能光伏发电及其应用[M]. 北京: 科学出版社, 2005: 27-28.

[15] 叶秋香. 光伏电池最大功率跟踪器的模糊控制及其应用[D]. 上海: 东华大学, 2006..

One Method of Maximum Power Point Tracking (MPPT)for Photovoltaic System

Li Chenxia1 Yang Honggeng1 Wang Yuanchi2
(College of Electrical Engineering and Information Technology, Sichuan University, Chengdu 610065;Leshan Power Supply Company, Sichuan Electric Power Company, Leshan, Sichuan 614000)

Maximum power point tracking (MPPT) can significantly increase conversion efficiency of photovoltaic (PV) cells. A fast maximum power point tracking (MPPT) algorithm is proposed in the paper. According to the derivative of power function expressed by voltage is zero at the maximum power point, getting the relation equation about Pmax and Umax, which is called maximum-power curve equation. The maximum power point is the intersecting point of the PV cells characteristic curve and the maximum-power curve. Searching the intersecting point with variable step on the two dimensional plane about power and voltage, finding the intersecting point means tracked the maximum power point.Simulation results validate that the proposed method can search the maximum power point of PV cells quickly and precisely, and eliminate the oscillation while operating at the maximum power point and improve the system stability.

photovoltaic cells ;Maximum Power Point Tracking（MPPT）;Maximum-power curve

李晨霞（1985-），女，硕士研究生，研究方向为电能质量与电力市场。