无铁心永磁直线同步电机电流鲁棒控制

孙宜标 刘 玲

（沈阳工业大学电气工程学院，沈阳 110870）

无铁心永磁直线同步电机电流鲁棒控制

孙宜标 刘 玲

（沈阳工业大学电气工程学院，沈阳 110870）

针对无铁心永磁直线同步电机（ILPMSM）存在d-q轴耦合效应、易受参数不确定性的影响，为实现系统的高性能控制，提出了一个带有延迟补偿的鲁棒控制器。该控制器由一个一阶参考模型的逆模型和一个积分项组成，不需要结合其他控制算法且不要求系统参数精确。采用系统传输延迟的逆模型来补偿系统时延的影响。与常规 PI控制器相比，鲁棒控制器能很好地抑制ILPMSM 系统的不确定性干扰，并对系统的传输延迟进行可靠补偿。仿真结果表明该方案有效地减少系统响应的超调，使系统具有良好的动态性能。

无铁心永磁直线同步电机；延迟补偿；鲁棒控制器；不确定性干扰

目前，将无铁心永磁直线同步电机控制系统用于高精度、短行程、高频往复运动的特殊应用场合，如半导体光刻、PC板检测和钻孔、凸轮的切削加工等，可充分发挥其质量轻、响应快、精度高的特点[1]。而用于高速加工的执行元件和控制技术受到很多因素的限制，为满足精密加工要求，研发高性能运动驱动器和伺服控制器是十分必要的[2]。

高速、高精无铁心永磁直线同步电机（ILPMSM）驱动器对制造业越来越重要，在数控机床中的应用也越来越广泛。ILPMSM的电枢绕组中没有铁心，不存在齿槽效应，产生的转矩脉动小，比有铁心永磁直线同步电机（PMLSM）实现更高的效率[3]。为了使永磁直线同步电机能在速度和位置控制方面达到完美的性能，最重要的是要控制好电枢电流，但是直线电机系统的电流控制性能会受到不确定的电流参数和反电动势（EMF）的影响[4-5]。

本文针对ILPMSM系统中由于d-q轴耦合效应和模型不确定性等因素造成的不良影响，基于电流环的控制策略应简单，系统响应快速、准确的思想，设计了带有延迟补偿的电流鲁棒控制器。该控制器由一个一阶参考模型的逆模型和一个积分项组成。为了补偿系统传输延迟对系统造成的反应超调的影响，在电流鲁棒控制器中加入了传输时延的逆模型。该控制器不需要结合其他控制算法且不要求系统参数精确。控制算法简单可靠，能有效提高系统暂态响应速度和减小稳态误差。

1 ILPMSM的数学模型

ILPMSM的d-q轴模型磁链方程[6]为

式中，ψd(ψq)为 d-(q-)轴磁链，Ld(Lq)是 d-(q-)轴电感，id(iq)为d-(q-)轴电流，ψf为定子永磁体产生的励磁磁链。

ILPMSM的d-q轴模型电压方程[7]为

式中，Vd(Vq)为 d-(q-)轴电压，Rs为动子电阻。emfd(emfd)是d-(q-)轴的反电动势，其表达式[8]为

式中，τ表示极距，υ为ILPMSM动子的运动速度，λ是永磁体的磁链系数。

2 鲁棒控制器设计

2.1 鲁棒控制方案

一阶被控对象P(s)可以表示为

式中，b和c是不确定的正常数，并且b≠c。

图1表示的是被控制对象 P(s)的控制框图，k为正常数，表示积分增益。Pˆ( s)是设计的参考模型，表达式为

式中，a为正实数。

图1 被控对象P(s)的控制框图

在鲁棒控制方案中，参考模型的阶次必须与实际模型的阶次相同[9]。由R(s)到Y(s)的闭环传递函数可以简化为

式中，k＞0，由 R(s)到 Y(s)的闭环传递函数是稳定的系统。

当R(s)是单位阶跃输入时，终值y(t)由下面的终值定理[10]得

从上式可以看出，控制策略使得被控闭环系统的直流增益为 1，系统稳态时的输出等于输入。进而说明，所提出的鲁棒控制策略简单，不需要结合其它的控制算法。将式（6）进行变换：

上式表明，当k越大，G(s)的响应越接近于Pˆ( s)的响应，并且有：如果k足够大，被控系统的响应与设计的参考模型基本一样。

事实上，设计的参考模型Pˆ( s)与实际模型 P(s)存在误差。如图2所示，将参考模型作为被控制对象，引入模型不确定性因子ρ。图中，d为不确定性干扰。ρ可通过以下式子计算得出

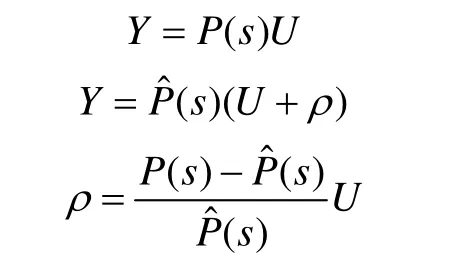
控制器的补偿项u(s)由下面式子给出

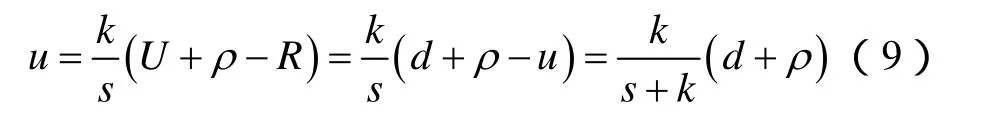
图2 带有干扰的被控对象P(s)的控制框图

当k足够大时，根据模型的不确定性，补偿项u跟踪不确定性干扰与参数不确定性的和。为了更清楚地看出鲁棒控制器能有效减少模型不确定性对电机运动造成的不良影响，给出剩余不确定性υk：

上式表明，当设计值k越大，υu就越小，不确定性干扰就越小甚至消除，最终，系统的响应与参考模型近似。

2.2 ILPMSM系统电流控制的鲁棒控制

根据式（2）和式（3）的拉氏变换式，可以得到如图3所示的由电压Vd(Vq)到电流id(iq)的开环控制框图。υd′ (υq′)是 d-(q-)轴控制器的控制项，kPWM是 PWM 调制解调器的转移因子。通过 kPWM，υd′ (υq′)转化成d-(q-)轴上的电压是 d-(q-)轴的电枢绕组电压。

图3 由电压Vd(Vq)到电流id(iq)的开环控制框图

提出的鲁棒控制策略用来控制 ILPMSM 的电流，可以减少如图4所示的d-q轴耦合效应和模型不确定性带来的干扰。图4是带延迟补偿的鲁棒控制器的控制框图。Ed(Eq)与反电动势相关，表示因耦合效应产生的干扰。i*d(i*q)是给定的 d-(q-)轴电流指令；υd′ (υq′)是 d-(q-)轴控制器的控制项；ucd(ucq)是d-(q-)轴控制器的补偿项；是设计的参考模型；轴的电流响应。是实际电流模型，可以写为

在图4中，e-Ls表示系统的传输延迟，L是系统的延迟时间，L=0.00005，该系统的传输延迟会影响系统性能和造成系统反应超调[11]。因此，在鲁棒控制器前面添加一个延迟补偿项eLs。延迟补偿项可以由泰勒级数扩展为

由于延迟时间非常小，因此上式的高阶项接近于零，从而可以被忽略。系统的传输延迟会因加入了延迟补偿项而被消除：

上式的近似只有当延迟非常小的时候才成立。

根据图1和图2的关系，图4可以等效为图5。在图5中，ρd(ρd)分别为d-(q-)轴模型不确定性因子，可以被提出的鲁棒控制器所补偿。

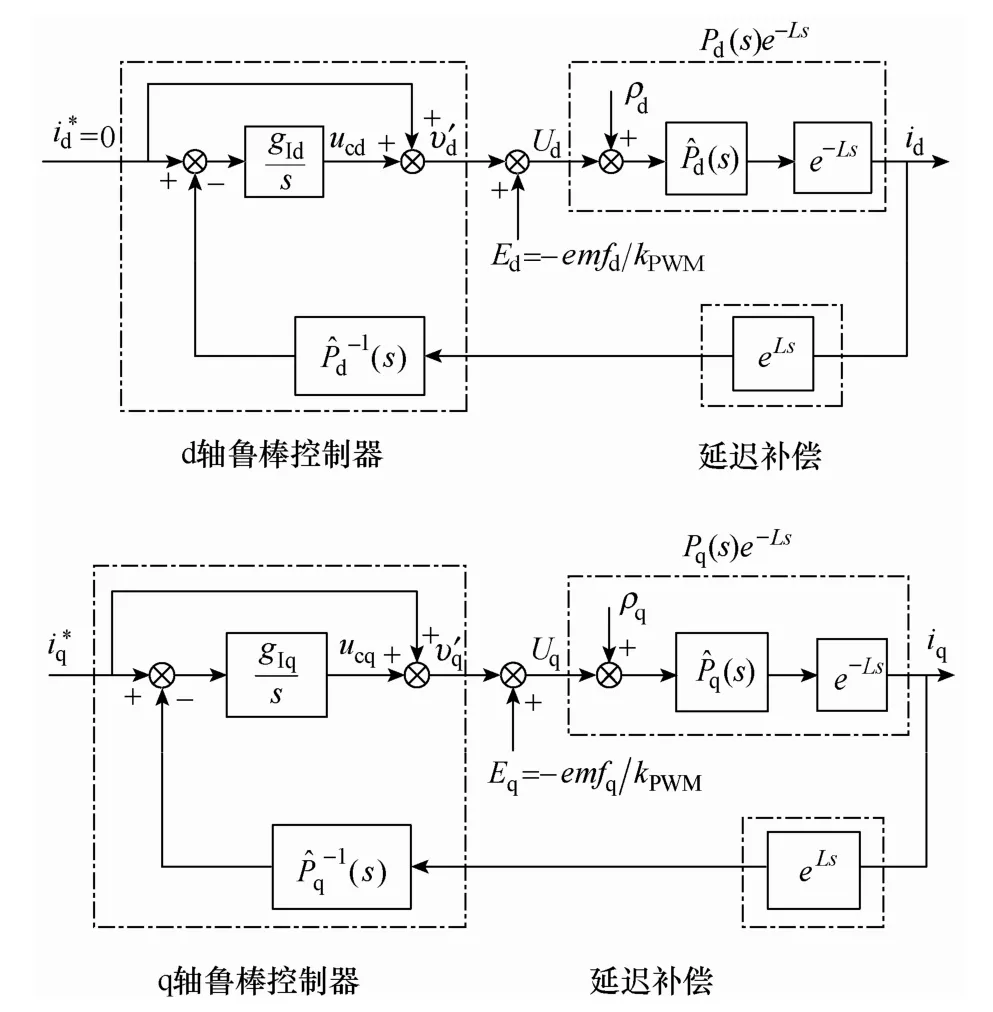
图5 d-(q-)轴电流鲁棒控制等效框图

由于系统的不确定性和延迟性可以被带有延迟补偿的鲁棒控制器所消除[12]，从而d-(q-)轴模型可以近似为如图6所示的理想的一阶模型这说明系统的直流增益为1。

图4 d-(q-)轴电流鲁棒控制框图

3 仿真结果

以美国Kollmorgen公司生产的型号为IL12-050的无铁心永磁直线同步电机为例，它具有连续的122N推力，可达到400N的峰值。其参数如下：动子电阻Rs=17.2Ω，电感L=6mH，额定电流In=2.1A，反电动势常数Ke=57V/m/s。

控制器的积分增益：gI=6500

传输延迟：L=0.00005s

干扰：d=0.1sin(1000t)A

当系统的电流控制采用PI控制器时，该闭环传递函数是个二阶系统，设置其参数：ωn=5204，ζ=0.707，KP=0.7266和 KI=4513。

图7为在给定电流指令*

id=0时，d轴电流的阶跃响应曲线保持为零。

图8为在无干扰时，采用PI控制器和鲁棒控制器的系统的电流阶跃响应曲线的对比。虚线表示给定的指令。从图中可以看出，采用鲁棒控制器的系统的电流阶跃响应与给定指令更加接近。在无干扰的情况下，采用PI控制器和鲁棒控制器的系统的稳态误差都是非常小的。

图9为有干扰时，采用PI控制器和鲁棒控制器的系统电流阶跃响应曲线的对比。虚线表示给定的指令。可以看出，鲁棒控制器对系统干扰的抑制效果要优于PI控制器。也就是说，提出的电流鲁棒控制器能较好的抑制 d-q耦合效应和参数不确定性给系统带来的干扰。

4 结论

在交流伺服系统控制中，电流环的响应速度要远远大于速度环和位置环，为了保证电机定子电流响应的快速性，电流控制器的实现不应太复杂。本文在分析了ILPMSM数学模型的基础上，对无铁心永磁直线同步电机系统的电流控制提出了一个带有延迟补偿的鲁棒控制器。通过对控制系统的电流阶跃响应进行仿真分析，证明了控制策略的有效性和可靠性，为直线电机的鲁棒控制提供了理论依据。

[1] 郭庆鼎，孙宜标，王丽梅. 现代永磁电动机交流伺服系统[M]. 北京：中国电力出版社, 2006: 138-146.

[2] 李义强，周惠兴. 精密伺服用无铁心永磁同步直线电动机研究综述[J]. 微电机, 2008, 41(5): 71-76.

[3] 刘晓，张玉秋，叶云岳，等. 双边空心式永磁直线伺服电机的空载磁场分析. 电机与控制学报, 2010,14(1): 56-60.

[4] 张代林，陈幼平，艾武，等. 基于观测器模型的直线电机干扰抑制技术的研究[J]. 中国电子工程学报,2007, 27(12): 14-18.

[5] ZHU Y W, CHO Y Y. Thrust ripples suppression of permanent magnet linear synchronous motor[J]. IEEE Trans. On Magnetics, 2007, 43(6): 2537-2538.

[6] 王丽梅，赵艇. 永磁同步直线电机鲁棒自适应位置控制[J]. 沈阳工业大学学报, 2008, 30(1): 15-18.

[7] XU J X, YAN R. On repetitive learning control for periodic tracking tasks[J]. IEEE Trans. on Automatic Control, 2006, 51(11): 1842-1847.

[8] ZHOU L, SHE J H, WU M, et al. Design of a robust modified repetitive-control system for a periodic plant[J]. ASME J of Dynamic Systems, Measurement and Control, 2012, 134(1): 1-7.

[9] NAGASHIMA M, USUI K, KOBAYASHI M. Rejection of unknown periodic disturbances in magnetic hard disk drives[J]. IEEE Trans. Magn., 2007, 43(9):3774-3778.

[10] TOMIZUKA M. Dealing with periodic disturbances in controls of mechanical systems[J]. Annual Reviews in Control, 2008, 32(2): 193-199.

[11] 鲁文其，胡育文，梁骄雁，等. 永磁同步电机伺服系统抗扰动自适应控制[J]. 中国电机工程学报, 2011,31(3): 75-81.

[12] 孙晓东，朱熀秋, 张涛, 等. 一种永磁同步电机解耦控制的新方法[J]. 微电机, 2010, 43(1): 61-65.

Current Robust Control for Ironless Linear Permanent Magnet Synchronous Motor

Sun Yibiao Liu Ling
(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870)

For the characteristics of ironless linear permanent magnet synchronous motor(ILPMSM) system being influenced by disturbance due to d-q axis coupling effect and parameters varieties, the investigated robust controller with system delay compensation is desired to achieve high performance. The proposed controller consists of an inverse of the first-order reference model and integral term. The proposed algorithm does not need to be combined with other control algorithms and the system parameters are not required to be known precisely. The system delay compensation adopts an inverse system delay model to compensate the system transport delay effect. Compared with PI controller, robust controller can restrain the effects of uncertainty disturbances and compensate for system transport delay in the ILPMSM system. Simulation result confirms the control scheme can reduce the overstrike of system with good dynamic response and dynamic characteristics.

ILPMSM; delay compensation; robust controller; uncertainty disturbances

教育部博士学科点专项科研基金项目（20102102110001）

孙宜标（1970-），男，安徽巢湖人，沈阳工业大学副教授，博士，主要研究方向为交流伺服系统、鲁棒控制、非线性系统。