采用压缩感知的标准测控信号处理*

黄 凌

（中国西南电子技术研究所，成都 610036）

采用压缩感知的标准测控信号处理*

黄 凌＊＊

（中国西南电子技术研究所，成都 610036）

针对测控通信信号接收端存在数据大量冗余的问题，利用标准测控信号在频域上的稀疏性，采用压缩感知的理论进行前期处理。分别考虑了只存在测距音、只存在遥测信号和两类信号都存在等三种条件下的信号处理问题。通过改变稀疏度的大小，可以在不影响解调性能的条件下，大幅度降低接收端所需要的采样率，并且达到消除系统中不需要的谐波的目的。仿真验证了方法的有效性，同时说明利用压缩感知技术，将为测控通信系统的射频直接采样和处理提供一种高效的方式。

测控通信系统;标准测控体制;压缩感知;频域稀疏;OMP算法

1 引言

测控通信是指对航天飞行器、临近空间飞行器和航空飞行器等进行跟踪测轨、遥测、遥控和信息传输［1］。现在的测控通信体制主要包括标准体制和扩频体制。在标准体制中，随着近年来射频采样技术的兴起，接收机端所需要存储传输的数据量变得很大，给后端FPGA和DSP处理带来了较大的压力。但是实际上这些数据具有很大的冗余性，即接收端并不需要处理全部的数据，而只需要一部分就可以完成系统所需要的功能。为了处理射频采样后带来的高速数据率问题，现有的方法包括多相滤波［2］、带通采样等方法，但是多相滤波实现比较复杂，所需资源较多，而带通采样能够处理的场景有限，因此迫切需要新的方法来应对测控体制中的射频采样后处理问题。

压缩感知作为近年来兴起的一门信号处理技术，已经广泛应用在雷达成像［3］、医学信号处理［4］、信道估计［5］和模式识别［6］等研究中，并得到了很大的发展。本文将压缩感知方法应用于标准测控通信信号的处理中，首先分析了测控信号的频域稀疏性，然后给出压缩感知的处理框架并采用自适应调整稀疏度的方法进行信号的重构，最后仿真验证了压缩感知技术不仅可以实现信号的重构，而且能在一定条件下达到消除系统中干扰的目的。

2 标准测控通信信号的稀疏性

标准测控通信也称为统一载波测控通信，是将多种功能的信号分别调制到不同的副载波上，然后再调制到一个统一的载波上，最后在射频上发射出去的测控体制。其一般的中频信号形式如式（1）所示:

标准测控信号工作在S频段，虽然实际信号带宽不超过3 MHz，但由于其载波频率变化范围为2.2～2.3 GHz，若要直接在S频段实现数字化，那么根据带通采样定理，在射频采样端所需要的采样率必须大于200 MHz。一般取为400 MHz以上，造成采样数据很大，这样对后端的信号处理和存储传输过程是不利的。图1显示了式（1）所示的测控通信信号在频域上的分布图，为便于仿真，其中信号中频为70 MHz;两个测距音分别为100 kHz和20 kHz，调制指数都设为0.7;遥测信号的副载波为300 kHz，数据速率为50 kb/s，调制指数为0.8。图中显示的频率范围从67～73 MHz，从中可以明显看出，信号只分布在中频附近，而在其他频段的值很小，也就是在100 MHz的带宽中，只有一段频率是存在信号的，所以其在频域上具有明显的稀疏性。

图1 测控通信信号的频域分布Fig.1 Frequency domain of TT＆C signal

3 压缩感知技术

压缩感知是近年来在信号处理领域出现的一种新的采样、编码技术。如果需要处理的信号具有某种稀疏性，那么就可以通过压缩测量技术在低于奈奎斯特采样速率的条件下对信号进行采样，并利用有效的重构算法从采样数据中近似恢复出原信号。典型的压缩感知信号处理模型如图2所示。

图2 压缩感知信号处理模型Fig.2 Compressed sensing model

3.1 信号稀疏表示

压缩感知处理的信号必须具有先验的稀疏性。若一个信号x∈RN只具有很少的非零值，那么称信号是稀疏的，而信号非零值的个数K=||x||0称为信号的稀疏度。在实际中所指的稀疏信号是表示时域上具有稀疏性，而在现实中，只有很少的信号具有时域上的稀疏性，比如雷达回波信号和超宽带通信信号等。而大部分的信号是在某个变换域中具有对应的稀疏性，即存在一组变换稀疏基 Ψ=［ψ1，ψ2，…，ψN］使得信号可以表示为

若系数矢量f只有K＜＜N个非零值，则称信号x在变换基Ψ上是K－稀疏的。典型的，图像信号的稀疏基是小波基和离散余弦基等，而由上文看出，测控通信信号的稀疏性体现在频域上，那么可以选用的稀疏基就有正交傅里叶变换基，本文也选用这种基底进行后续的处理。

3.2 压缩采样

压缩采样方法是压缩感知技术不同于传统的奈奎斯特采样的关键。通俗地说，压缩采样就是将传统信号处理中的压缩和采样过程融合在一个过程中，即通过一个设定的观测矩阵Φ∈RM×N，对信号x进行线性投影，得到M×1的观测数据

如果取M=N，那么压缩采样就等同于奈奎斯特采样，而在压缩采样中，所需要的观测数据远小于原始数据，即满足M＜＜N。

值得注意的是，观测矩阵的选取必须满足一定的条件，才能重构出原始的信号。实际中经常使用的限制条件称为约束等距特性（RIP）［7］。具体定义如下:对任一K－稀疏信号α若存在δk∈（0，1）值，使得满足

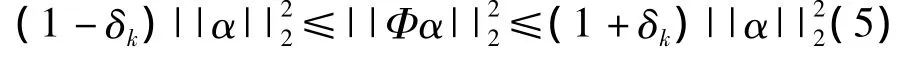
则称Φ满足K阶RIP特性。可以证明，若观测矩阵满足2K阶RIP特性，则可以从观测数据y完美地重构原始信号x。通常情况下，观测矩阵可以选取为高斯随机矩阵、伯努利矩阵和广义正交集矩阵，因为这些矩阵都具有较好的RIP特性。

3.3 信号重构

信号重构是指利用压缩采样得到的数据恢复出原始的信号。由于采样数据的长度M远小于原始数据的长度N，因此这类问题是欠定的，即可能有无穷多组解。但是，由于信号具有稀疏性，那么在这些解的集合中，我们需要选取稀疏性最大的那一组。用数学语言可描述最小l0范数问题:

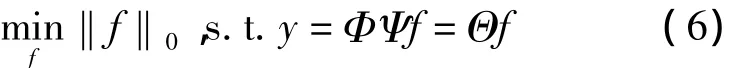
其中，矩阵Θ=ΦΨ称为传感矩阵。但是这个问题的求解是一个NP难问题，是很难直接求解的。求解此问题的一类有效方法是贪婪迭代算法，它将稀疏重构问题转化成迭代二乘估计问题，通过迭代循环来识别信号的稀疏支撑集来构建信号在支撑集上的最小二乘逼近。典型的贪婪迭代算法有OMP算法、StOMP算法和CoSaMP/SP算法等，它们的不同之处在于对信号稀疏支撑集的识别方式不同。下面简要介绍OMP算法［8］的处理流程:

实际中OMP算法通常以信号的稀疏度K作为完成重构的最大迭代次数，在稀疏度比较大的情况下，这会带来较大的计算复杂度。但是在下面的仿真实验中，我们会发现通过灵活选取需要的稀疏度，可以在测控通信信号的处理中带来更大的益处。

4 仿真实验

在仿真中，将考虑3种情况，即只有测距音、只有遥测信号和两种信号都存在的条件下进行实验，以验证压缩感知方法能够用于测控通信信号的处理。

4.1 只有测距音的压缩感知

设定测控信号的测距音分别为100 kHz和20 kHz，为了使频率分辨地更加清楚，此处设定中频为5 MHz;调制指数都设为0.7，信噪比为20 dB。由于射频带宽为100 MHz，采用的射频采样率为200 MHz，仿真时间为10－5s，在压缩采样中原始信号有2 000个点，图3中分别显示了在采用压缩感知方法时，降低采样率至40 MHz，则采样点数M=400和设定稀疏度K=50时的信号对比、原始信号幅度谱和恢复信号幅度谱。由图中明显可以看出，信号得到了很好的重构，两条测距音的谱线非常明显，但是有些不需要的谐波曲线也被恢复出来，而这些谐波信号对后续的解调处理是无用的，因此没有必要进行恢复。

图3 完全重构时的性能比较Fig.3 Performance comparison in complete recovery

下面改变采样率和稀疏度，采样率进一步降低至20 MHz，则采样点数设为M=200和稀疏度K=10，图4中分别显示了信号对比和重构信号的幅度谱。可以看出，虽然信号没有被很好地重构，但是将一些不需要的谐波信号完全滤除，只剩下了需要的两组测距音，因此这样的重构效果是更为有利的。

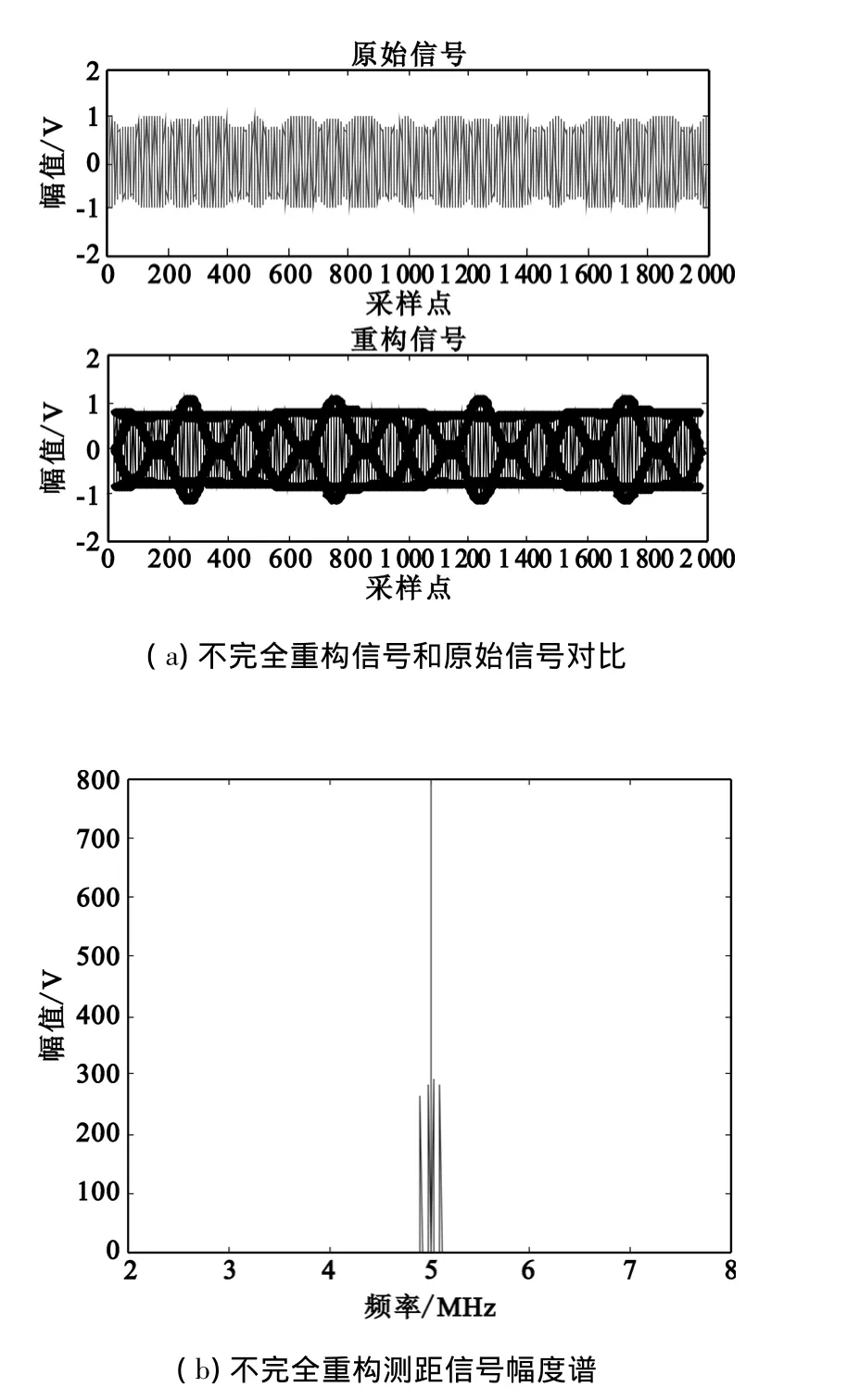
图4 不完全重构时的性能比较Fig.4 Performance comparison in part recovery

4.2 只有遥测信号的压缩感知

设定遥测信号的信息速率为50 kb/s，遥测副载波为300 kHz，调制指数为 0.8，中频设为4 MHz，信噪比为10 dB，射频采样率为200 MHz，原始信号点数为2 000点。压缩采样率为40 MHz，采样点数M=400和稀疏度K=50。图5中分别显示了原始信号和恢复信号的幅度谱，由图中可以看出，恢复出来的信号中保留了2倍信号带宽内的所有信息，而在后续的解调处理中，低通滤波器的截止带宽一般也设为2倍信号带宽，因而此带宽外的大部分信号都是无用的。表1给出了解调后的数据与输入信息码元，可以看出，所有码元都得到了正确的解调。

图5 遥测信号的压缩感知性能Fig.5 CS performance of telemetry signal

图6 测控信号的压缩感知性能Fig.6 CS performance of TT＆C signal

表1 无测距音重构判决码元与原始码元比较Table 1 Original and recovery symbols without ranging tone

表2 重构判决码元与原始码元比较Table 2 Original and recovery symbols in TT＆C

4.3 测距音和遥测信号都存在的压缩感知

综合上述两种情况，实验中设定测距音分别为100 kHz和20 kHz，调制指数都为 0.7，信息速率为50 kHz，遥测副载波为300 kHz，调制指数为 0.8，信噪比为10 dB，射频采样率为200 MHz，原始信号点数为2 000。压缩采样率为40 MHz，采样点数M=400和稀疏度K=50。图6中分别显示了原始测控信号和恢复信号的幅度谱，从图中可以看出，对解调端有用的谱信号都得到了很好的保留，而无用的分量都有效地被滤除。表2显示了遥测信息解调的结果，可以看出信息都被正确地判决出来。

4.4 仿真实验总结

从以上的仿真中可以得出以下结论:

（1）测控信号中存在着大量的冗余信息，即只需要对应信号的的数据量就可以恢复出原信号;

（2）通过改变OMP算法中的稀疏度，可以达到滤除不需要的信号频谱分量的目的，这对于后端的解调处理没有任何影响;

（3）压缩感知方法对于标准体制中的测控信号处理过程是类似的，即可以用同一套系统参数进行不同条件下的信号采样和恢复。

5 结束语

本文将压缩感知方法应用于测控通信信号的处理中，通过灵活地改变稀疏度的方法，能够在不影响后端解调性能的条件下，将所需要的采样率大幅度降低至原采样率的10% ～20%，并且可以消除信号中一些不需要的杂波分量。后续的研究将考虑在扩频体制下的压缩感知的可行性，以及如何将这种方法应用于硬件的实现方面。

［1］ 刘嘉兴.飞行器测控通信工程［M］.北京:国防工业出版社，2010.

LIU Jia－xing.Spacecraft TT＆C and Communication Engineering［M］.Beijing:National Defense Industry Press，2010.（in Chinese）

［2］ 何子述，夏威.现代数字信号处理及其应用［M］.北京:清华大学出版社，2009.

HE Zi－ shu，XIA Wei.Advanced DigitalSignal Processing and Application［M］.Beijing:Tsinghua University Press，2009.（in Chinese）

［3］Potter L C，Ertin E，Parker J T，et al.Sparsity and Compressed Sensing in Radar Imaging［J］.Proceedings of IEEE，2010，99（6）:1006 －1020.

［4］Yang J，Wright J，Huang T，et al.Image super－ resolution as sparse representation of raw image patches［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Anchorage，AK:IEEE，2008:1 －8.

［5］Haupt J，Bajwa W U，Raz G，et al.Toeplitz compressed sensing matrices with applications to sparse channel estimation［J］.IEEE Transactions on Information Theory，2010 ，56（11）:5862－5875.

［6］Meng Deyu，Yee Leung，Xu Zongben，et al.Improving geodesic distance estimation based on locally linear assumption［J］.Pattern Recognition Letters，2008，29（7）:862 －870.

［7］Donoho D L.Compressed Sensing［J］.IEEE Transaction on Information Theory，2006，52（4）:1289 －1306.

［8］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transaction on Information Theory，2007，53（12）:4655 －4666.

黄 凌（1978—），男，重庆人，2009年于电子科技大学获硕士学位，现为工程师，主要研究方向为航天器测控通信技术。

HUANG Ling was born in Chongqing，in 1978.He received the M.S.degree from University of Electronic Science and Technology of China in 2009.He is now an engineer.His research concerns spacecraft TT＆C.

Email:hltony@126.com

A TT＆C Signal Processing Method Based on Compressed Sensing

HUANG Ling
（Sowthwest China Institute of Electronic Technology，Chengdu 610036，China）

In TT＆C signal processing，the

data is always redundant.To solve this problem，a method based on compressed sensing（CS）is proposed by efficiently using the sparsity of TT＆C signal.Three conditons of signal processing are considered，including only range measurement signal existing，only data signal existing and both of them existing.As the change of sparsity degree，the sampling rate is greatly reduced without influencing the demodulation performance，at the same time，some unused harmonic is eliminated from the whole system.The efficiency of the method is verified by simulations.The result implies that compressed sensing provides an efficient way for RF sampling and processing in TT＆C system.

TT＆C and communication system;standard TT＆C;compressed sensing;frequency domain sparsity;OMP algorithm

TN911.7

A

1001－893X（2014）05－0578－06

10.3969/j.issn.1001 －893x.2014.05.010

黄凌.采用压缩感知的标准测控信号处理［J］.电讯技术，2014，54（5）:578－583.［HUANG Ling.A TT＆C Signal Processing Method Based on Compressed Sensing［J］.Telecommunication Engineering，2014，54（5）:578 －583.］

2013－12－12;

2014－03－06 Received date:2013－12－12;Revised date:2014－03－06

＊＊

hltony@126.com Corresponding author:hltony@126.com