信息技术与变式学习有机融合打造高效数学课堂

◆周宝峰 许伟伟

信息技术与变式学习有机融合打造高效数学课堂

◆周宝峰 许伟伟

变式教学经过教师探究和摸索已经比较成熟，随着现代化教学手段的改进，实现信息技术与变式学习有机融合，能够激活数学课堂，“减负增效”，从而打造高效课堂。

信息技术；变式教学；数学

经过多年的实践和研究，“变式”教学模式已经充分显示出它优异的教学效果。特别是在数学课上，教师通过一系列的“变”能更好地促进学生数学素养的形成，给学生提供一个求异、思变的宽松的创新氛围和无限的想象空间，让学生从差异中去比较、鉴别。这样在一定程度上，把知识系统化、体系化，也很大程度地减轻学生的负担，使知识灵活变通，对扩展学生思维有很大帮助，毕竟这些“变”是教师知识和经验的总结，是教师的精华。

笔者在这里提出的是学生的“变式”。笔者在教学中很注重知识的归纳和总结，学生潜移默化地受这种思维方式的熏陶，自觉不自觉地会主动去变，变着有意思，越变越想变，而且学生通过自己学习和小组合作，互相借鉴思维，整合出一套“变”，把知识层层深化、扩展，从而变知识为自己的。经过几年的实践证明，这种变式来源于教师的“变”，比教师的“变”更深刻，甚至学生的有些“变”是教师所想不到的。这样在课堂上就形成一种学习研究的氛围，课堂不再只是教师的天下，同样也是学生能力展现的舞台。其中充分运用现代化教学手段——多媒体，比如幻灯片（PPT）、Word、几何画板、电子白板等，通过静态和动态的展示，辅助打造高效课堂。下面结合几个案例，笔者谈几点感受。

【案例一】在讲授反比例函数的性质时，反比例的增减性是最重要的，同时也是难点，学生往往忽略“在同一象限”这个条件，吃不透它与一次函数的增减性有什么区别，认为这个条件是多余的。但有一个小组的学生就将这一难点通过变式轻松解决。

图1

学生甲：如图1所示，已知点(1,y1)(2,y2)(3,y3)在反的图象上，比较y1、y2、y3的大小。（解答：当k＜0时，y随x的增大而增大，也可以把1、2、3分别代入，得到相应的函数值来比较。）

学生乙：把-6改为2呢？（学生提问学生，简单就可以答出。）

学生丙：把-6改为-k2-1呢？（学生提问学生，代入不行了，只能用增减性了。）

学生丁：把(1,y1)(2,y2)(3,y3)改为(-1,y1)(2,y2)(3,y3)呢？（学生提问学生。）

这里很易得出错误答案，y1＞y2＞y3。解决办法：可以带入求函数值得到y1＞y3＞y2。也可以用图像法，如图2所示。

经过以上分析，学生明白了“在同一象限”这个条件的重要性。接着学生又进行变式。

学生丁：把(-1,y1)(2,y2)(3,y3)改为(x1,y1)(x2,y2)(x3,y3)，且x1＜x2＜0＜x3呢？（学生提问学生。）

图2

通过上述层层递进，学生就明白了为什么，他们借助白板不断地变，数形结合，轻松攻克难点。而这些变式只要用PPT做一张幻灯片，然后用电子白板的书写功能就能实现。

【案例二】在复习函数性质时，学生甲给出这样一道题：如图3所示，反比例函数 的图象与一次函数y=kx+b的图象交于两点M(1,3)、N，N的纵坐标为-1，求何时

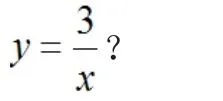
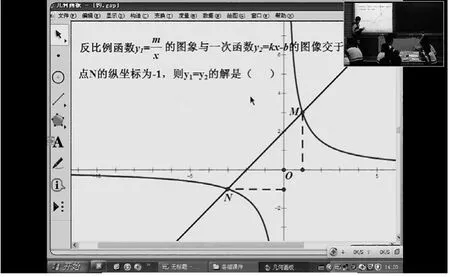
图3

学生乙变式出：何时y1＜y2？何时y1＞y2？

如图4、图5所示，通过白板的书写功能，标注功能，数形结合，把看上去很难的题形象地刻画出来，学生理解起来简单、易懂。其中一个学生在讲解时丢掉了x=0这一分界线，其他学生上台在白板上予以纠错。经过这个探究的过程，学生理解起来就更加深刻了。

学生丙又变式出：若再增加一条直线y3，这时y1、y2、y3有何大小关系？

图4

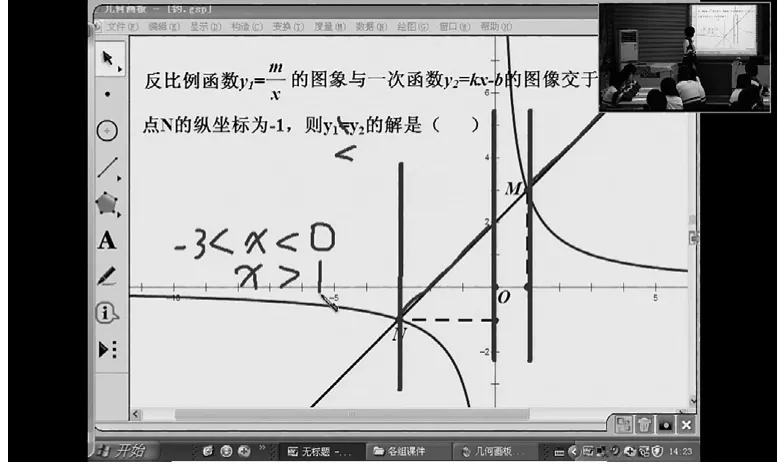
图5

图6

这道题在中考中是难度较大的题：三个函数比较大小。但这个小组通过设计把这道题层层加大难度，一步一步解决，借助多媒体轻而易举地解决掉。他们这种由浅入深的剖析肯定是下了一番功夫，能不提高数学能力吗？他们把这么优秀的东西分享给其他学生，其他学生不也受益匪浅吗？

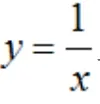
这道题看上去也很复杂，学生甲运用几何画板将其简单、形象地解答出来了，如图7、图8所示，从而3-1=2。这比单纯地讲解更容易理解和接受，也显现出几何画板在数学课上的重要性。

这样又把问题加深了，但在前面学生的讲解下，这道题就水到渠成了。

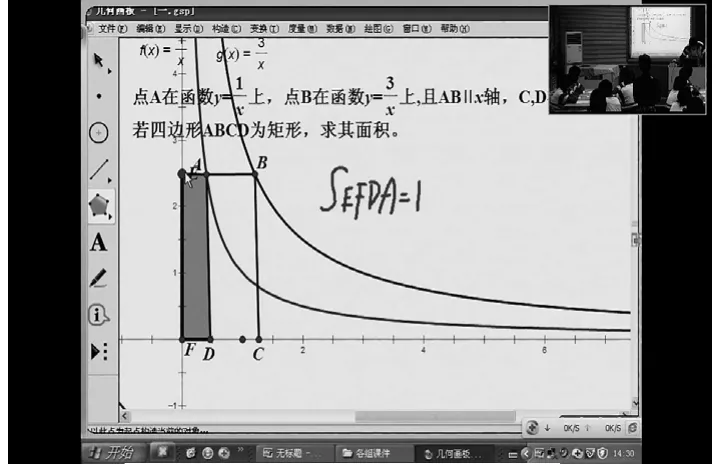
图7

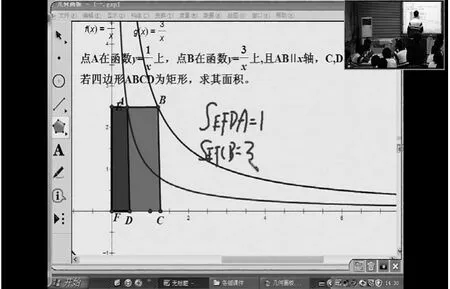
图8

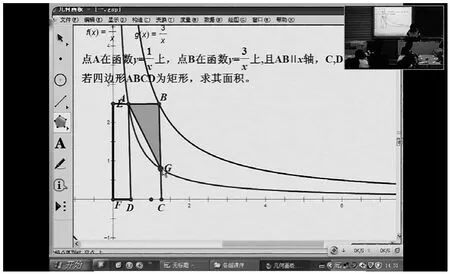
图9

因此，学生的“变式”以问题作为主线，探中有究，究中有探，具有启发性，有目的、有方向、有层次。不仅能使学生对所学知识不断深化，而且让学生深层地认识问题的本质，领悟数学方法的实质。让学生积极地探、层层深入地探、灵活地探、发散地探、创新地探，这是他们自己研究的成果，不论是从“质”还是从“量”，都比教师的“变式”更有效果，从而有效地提高初中数学课堂教学的效益。当然，把计算机作为新教学媒体用于课堂教学中，运用课件动态演示，可把知识的形成过程直观、生动、便捷地展示在学生面前，帮助学生掌握其内在规律，完成知识构建，为数学学习和运用提供一个无与伦比的广阔舞台。这样会提高学生数学水平和能力，增强学生的创新意识和应变能力，优化学生的思维品质，更好地促进学生数学素养的形成，也真正把课堂还给学生，让学生主动参与教学活动，获取知识，学会方法，实现由“要我学”到“我要学”的转化。

当然，这样的教学，从表面上看，好像是解放了教师，教师的地位在下降，教师的任务在减轻，其实不然，这对教师要求更高。因为学生的“变”有些是重复的，意义不大的，或偏离课程标准的，也或者是教师所预设不到的，教师也要跟着学生思考，和学生一块探究，适当调控，适当干预，适当讲解。不得不说，学生的一些方法有时是教师所不能及的。因此，这样的“变式”教学对教师提出更高的要求。

这样的课，笔者在新授课里试验过，学生要想挖出课的真正内涵，需要大量的预习工作，课上也需要给出大量的时间让学生去整合、借鉴，可能花费较大时间，但那是他们智慧和努力探究的结晶，所以他们理解得更透彻，应用起来更熟练。复习课也很适用。通过新授课的学习，学生对知识点的把握提高了，在复习时就可以提出更多的想法，变出更综合的题来。当然无论是新授课还是复习课，学生的变可能会跑偏，也可能会变得不彻底，这时教师就需要引导了，教师的作用还是很重要的。这样一节课下来，还有打瞌睡的学生吗？还有抄作业的现象吗？这样的课堂才是研究性的课堂，才是学生的课堂。

G434

B

1671-489X(2014)17-0051-03

10.3969/j.issn.1671-489X.2014.17.051

作者：周宝峰，中学二级教师，淄博市周村区第三中学政教处副主任；许伟伟，中学一级教师，淄博市周村区第三中学，主要从事课堂研究，参与省级课题“建模在数学中的应用”（255300）。