基于元样本稀疏表示的目标跟踪算法

张 英，樊亚翔，孙 浩，计科峰

(国防科技大学电子科学与工程学院，长沙 410073)

基于元样本稀疏表示的目标跟踪算法

张 英，樊亚翔，孙 浩，计科峰

(国防科技大学电子科学与工程学院，长沙 410073)

近年来，稀疏表示被引入视频目标跟踪问题中。在粒子滤波框架下，视频跟踪问题被看作是使用若干个目标模板来稀疏化线性表示候选区域的过程，并使用“小模板”来处理目标物在视频场景中出现的各种复杂变化。但算法没能利用模板的本质特性，复杂度高。基于元样本稀疏表示提出一种目标跟踪算法，提取目标模板的元样本建立目标词典，再针对目标遮挡情况引入遮挡词典，进而构造超完备词典;在跟踪阶段，采用了一种迭代的方法解决l1最小范数问题，计算稀疏表示系数。实验结果表明：提出的算法比文献中现有的基于l1范数最小化的跟踪方法性能更稳定、计算效率更高。

目标跟踪;稀疏表示;l1最小范数;元样本;主成分分析

视觉目标跟踪是计算机视觉研究领域的一个重要的研究方向，被广泛应用于智能视频监控、运动分析、运动识别以及人机交互等领域。目前已有大量学者对视频跟踪算法进行了广泛研究，提出了多种类型的跟踪算法，包括基于模板［1］、基于子空间分析［2］、在线分类［3］的跟踪算法等。最近，MEI等［4－5］将稀疏表示技术引入到视频目标跟踪任务中，将跟踪问题视为粒子滤波框架下的稀疏编码问题，提出了l1－跟踪子;同时，通过引入一组“小模板”(正模板和负模板)，使得算法能够鲁棒地处理目标物的形变、遮挡以及场景光照变化等一系列富有挑战性的问题，取得了良好的效果。但是该方法直接使用图像模板作为词典，且目标模板较多，导致算法的复杂度高、计算量大。此外，这种方法没有注意到图像本质上稀疏冗余的特点，利用目标模板的本质信息来表示目标，导致当目标姿态发生变化时，跟踪不够稳定。

元样本可以看作样本基因表达的线性组合，并且包含数据的本征结构［6］。所有的样本都可以由元样本来进行线性表示。对于跟踪问题，待跟踪目标可以看作它的目标模板元样本的线性表示。

根据上述情况，本文提出了一种基于元样本稀疏表示的目标跟踪算法。通过大量比较实验，验证了该方法的跟踪精度比原始l1－跟踪子好，跟踪效率也有了一定的提升，对于分辨率较高的视频跟踪效果更好。

1 基于稀疏的目标跟踪算法

1.1 目标的稀疏表示

稀疏表示理论有其认知学背景，并被应用于字典构建、图像分类等领域［7］。理论和实验表明，基于稀疏表示的样本相似性度量具有判别性，一个样本通常仅由其同类样本线性加权获得，从而更好地刻画样本间的相似度信息。

稀疏表示模型认为自然信号能够被简洁地表示，或逼近成预先定义的原子信号的线性组合，而且这些组合系数是稀疏的，即只有少数不为零的系数。直观地，稀疏性可以由稀疏向量非零的个数来表示，也就是用l0范数来测量，形式描述如下：假设存在一个过完备的字典A∈Rm×n，则样本y∈Rm被表示为：

式(1)中：ε是误差容限，‖·‖0代表l0范数，向量中非零元素的个数。l0范数最小化问题是一个NP难题。如果问题的解足够稀疏，l1范数最小化，由于其与l0范数最小化的凸函数最接近，两者是等价的，即也可以表示如下：

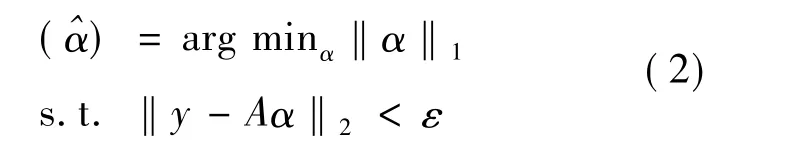
对于上述最优化问题，有许多方法能够有效地求解，包括匹配追踪算法(MP)、正交匹配追踪算法(OMP)等方法［8］。

1.2 基于稀疏表示的目标跟踪算法

MEI等提出基于稀疏表示的目标跟踪，其基本思想是：不同视角、不同光照条件下的目标图像，可以近似地认为是处在一个低维的子空间中，该子空间可由一系列的目标模板构成。为了跟踪一个目标，首先需要通过l1范数最小化对每一个候选目标(粒子滤波产生的粒子)用琐碎模板和目标模板进行稀疏表示计算，然后在所有的候选目标当中选择具有最大概率的候选目标(粒子)作为当前帧跟踪结果，再在下一帧中继续采用粒子滤波器来产生候选目标(粒子)，并重复进行。

简要过程如下：首先定义一个目标模板集合T=［t1，t2，…，tn］∈Rm×n。这个目标模板集合包含了n个目标模板(通过将目标模板灰度图像变化成一个m维列向量)。跟踪结果y就可以通过目标模板集合的线性约束来逼近，如下公式所示：

其中，a= [a1，a2，…，an]T∈Rn即为目标物的稀疏表示系数。考虑到目标被遮挡的情况，引入误差向量e来描述图像中的遮挡部分，则目标图像可以按下式估计得到：

其中：I∈Rn×n是单位矩阵，为处理噪声的小的模板集。若记 D=[T，E]，c=[a，e]T，式(4)可以改写为一个l1范数最小化问题：

2 基于元样本稀疏表示的目标跟踪算法

2.1 目标模板的元样本

元样本的概念是从生物学基因表达的角度提出的。元样本可以看作它基因表达数据的线性组合，能俘获数据的本质信息。所有的样本都可以由元样本来进行线性表示。对于维数较高的样本数据，通过计算其元样本来表示数据，不仅能够获取数据的本质结构，还起到数据降维的作用，加快后续计算速度。

数学上，将数据矩阵T分解为2个矩阵：

其中：矩阵T表示m×n的原始数据集，每列为一个样本的数据，每行表示数据的特征;矩阵W大小为m×p，其中每一列定义为一个元样本;矩阵H大小为p×n，其中每一行的n个系数代表了相应样本在元样本上的表达模式，如图1所示。

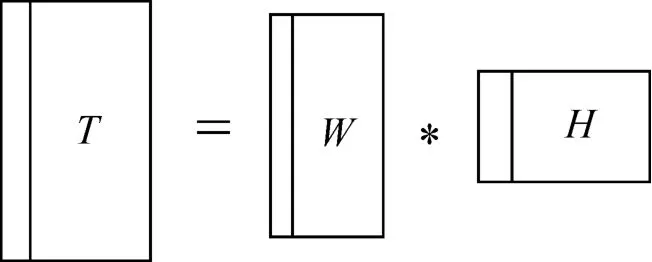
图1 目标模板数据的元样本

用于元样本提取的方法有很多，如主分量分析(PCA)、奇异值分解(SVD)、非负矩阵因式分解(NMF)以及独立分量分析(ICA)等。

2.2 基于元样本稀疏表示的目标跟踪算法

元样本包含了目标模板样本的内在结构，可以采用元样本代替训练数据中的目标模板来表示目标。分别从目标模板数据中提取元样本，为此将目标模板数据集矩阵T分解为2个矩阵：T～WH。其中：W是一个m×p的矩阵;H是一个p×n的矩阵;p是元样本的数目，在实验部分被确定。由于目标模板的PCA基具有仿射不变、尺度不变、对光照变化和姿态变化鲁棒性好的特点，能够获得目标模板的本质信息，因此选取PCA方法进行元样本提取。

图2 两种方法的区别

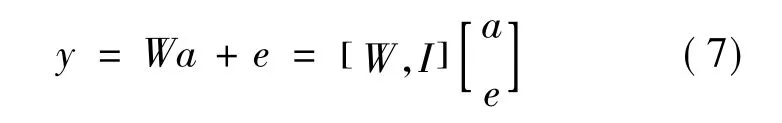
其中：I∈Rn×n是单位矩阵，为处理噪声的小的模板集;若记 D=[T，E]，c=[a，e]T，y=Dc。同样，类似式(5)、(7)可以转换为：

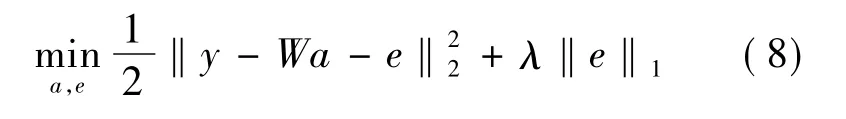
同样，目标图像可以通过下式估计得到：

因此，目标跟踪问题同样转换为一个求解l1最小范数问题，如图2所示。

在这里，首先说明式(5)和式(8)的区别：对于式(5)，目标模板和“小模板”的系数应该是稀疏的;对于式(8)，小模板是稀疏的，但是目标模板的元样本不是稀疏的。由于“小模板”的数量远大于目标模板的元样本数量，目标能够被目标模板和“小模板”一起稀疏表示，因此需要寻找新的算法来解等式(8)。

其中：y∈Rd×1表示目标向量;W∈Rd×k表示目标模板的元样本向量;a∈Rk×1表示稀疏表示系数;e∈Rd×1表示误差向量;λ为参数。由于式(9)没有封闭解法，采用一个迭代的方法来计算aopt和eopt：

①如果给定 eopt，式(9)就等于J( a)的最小值，其中J( a)=‖ ( y－eopt)－Wa。这是个最小二乘问题，aopt能够通过aopt=WT( y－eopt)获得。

②给定aopt，式(9)就等于G( e)的最小值，其中

通过步骤①和步骤②，式(9)的优化问题能够有效解决。

本文算法总结如下：

输入：某帧视频It，上一帧目标位置 Xt－1，目标模板T，粒子数量N

输出：每帧跟踪到的目标位置Xt及更新后的目标物模板T。

①初始化：以Xt－1为均值Σ为方差的高斯先验分布生成N个粒子 {：i=1，2，…n}，并设置各粒子的权值为=1/n;

③对于目标模板T，通过式(6)提取其元样本W;

⑦ 获取当前帧目标位置Xt=Σi，i=1，2，…，n;

⑧获取Xt对应的目标物特征yt，并计算其在过完备字典D上的稀疏系数ct;

⑨更新目标模板T。

对于上述算法中第⑨步的模板更新问题，采用一种基于误差门限的升级方法。在每帧跟踪目标获得最优的匹配模板后，抽取相应的图像基和误差矩阵;基于误差矩阵，计算它其中的非零系数比例η;然后根据η采用3种升级策略：完全升级、部分升级以及不升级。

3 实验结果与分析

为了验证算法的有效性，对一些标准的视频数据集进行了测试。算法在Matlab7.1下编程实现，实验的硬件平台为 3.3GHz Core2，内存为3GB。对于每个视频序列，手工标记了初始帧的目标位置。对于目标模板元样本提取，选择了PCA的方法，模板图像裁剪成32×32的大小，并且提取16个元样本作为目标模板。此外，选取了1 024个小模板。粒子数设置为N=600，跟踪器每隔5帧升级一次。整个实验中λ设置为0.05。

本文算法在3个公开的视频数据进行了一系列的实验，3个视频分别涉及到目标部分遮挡、光照变化、姿态的变化等挑战性的问题。本文实验使用的追踪视频如表1所示。本文算法与最近提出的目标追踪算法(多实例学习跟踪算法MIL［3］、增量学习跟踪算法IVT、基于稀疏表示的追踪算法L1［4］)进行比较。

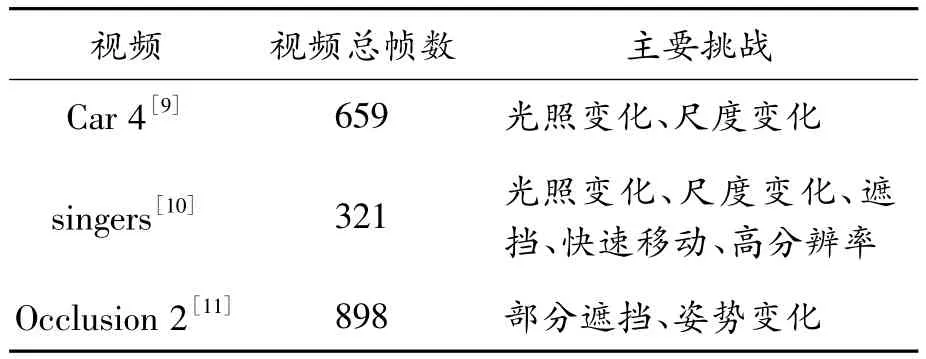
表1 实验采用的跟踪视频

图3分别是在Car 4、singers以及Occlusion2视频序列上实施上述4个实验的部分跟踪结果。由图中可以看出：对于遮挡、光照变化、旋转、尺度变化等问题，IVT算法、MIL算法以及L1算法都出现了不同程度的追踪目标漂移现象，比较得出本文算法跟踪效果较好、漂移较少、稳定性优于其他3类算法。

在定量分析方面，通过追踪目标中心位置与手动标记的真实中心位置，利用欧式距离进行对比，距离越大说明越偏移目标。对每隔5帧图像取一个手动标记的5帧图像中心的平均值与4个算法的实验结果进行比较，中心位置误差比较如表2所示。由表2可知：本文方法中心位置误差率与其他算法相比普遍减少20%以上，进一步说明了本文算法的稳定性。表3是3种算法的平均帧率比较。可以看到：本文方法效率高于L1算法。与其他3种方法相对比，本文算法在singers数据库上漂移最少、效率较高，证明了本文算法对于分辨率较高的视频跟踪有较好的效果。

图3 部分跟踪结果比较

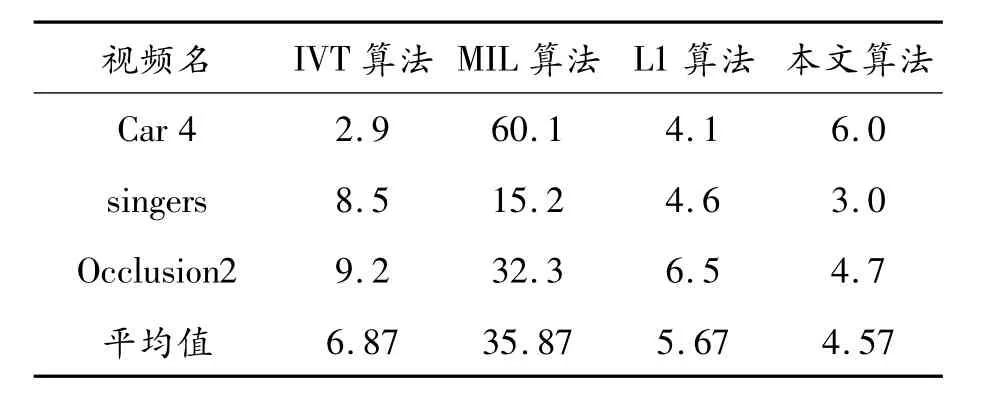
表2 算法平均中心位置误差(像素)

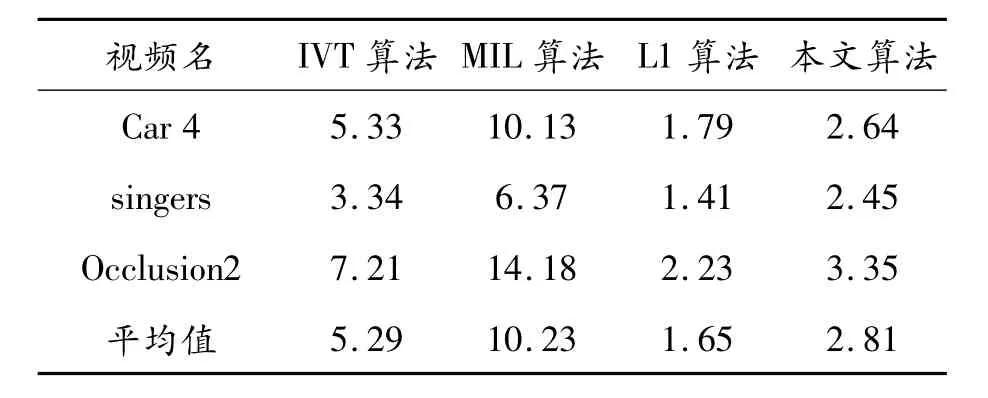
表3 跟踪平均帧率比较(帧/s)

4 结束语

本文针对原始l1－跟踪子效率低下的缺点，提取目标模板的元样本来代替目标模板表示目标，进行稀疏表示跟踪。该算法利用了目标模板的元样本信息，用目标模板的本质信息来表示目标，从而提高了算法的效率。在求解稀疏表示系数阶段，采用一种反复迭代的方法来解决l1最小范数问题。对标准的视频数据集进行了测试，结果证明该方法的鲁棒性和有效性。采用其他的元样本提取方法(如NMF)来代替目标模板以及进一步提升算法效率，将是我们下一步研究的重点。

［1］ Adam A，Rivlin E，and Shimshoni I.Robust fragments －based tracking using the integral histogram［J］.Proc.IEEE Conf.Comput.Vision Pattern Recognition，2006：798－805.

［2］ Wang T，Gu I Y H，Shi P.Object tracking using incremental 2d－pca learning and ml estimation［C］.Acoustics，Speech and Signal Processing 2007.In ICASSP，2007：933 －936.

［3］ Babenko B，Yang M H，Belongie S.Visual tracking with online multiple instance learning［C］.Proc.IEEE Conf.Comput.Vision Pattern Recognition，2009：983-990.

［4］ MEI Xue，LING Haibin.Robust visual tracking using L1 minimization［C］.Proceedings of the IEEE 12th International Conference on Computer Vision(ICCV 2009)，Kyoto，Japan：1436 －1443.

［5］ MEI Xue，LING Haibin.Robust visual tracking and vehicle classification via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33(11)：2259 －2272.

［6］ Brunet J P，Tamayo P，Golun T R，et al.Metagenes and molecular pattern discovery using matrix factorization［J］.National Academy of Sciences，2004，101(12)：4164－4169.

［7］ Wright J，Yang A Y，Ganesh A，et al.Robust face recognition via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31(2)：210－227.

［8］ 戴琼海，付长军，季向阳.压缩感知研究［J］.计算机学报，2011，34(3)：425 －434.

Object Tracking Algorithm Based on Sparse Representation for Meta-sample

ZHANG Ying，FAN Ya-xiang，SUN Hao，JI Ke-feng
(School of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China)

The research on sparse coding has been introduced into the issue of video object tracking recently.Under particle filter framework，the target template is represented by a set of all target candidates.Trivial templates are used to deal with complex changes of objects in video scenes.In this paper，however，the algorithm ignores the intrinsic information of the target candidates，so the cost is very expensive.This paper proposes an object tracking algorithm based sparse representation for metasample.A set of meta-samples were firstly extracted from all target candidates，then the trivial template were added into building the over complete dictionary.For tracking，an iterative algorithm was proposed to solve l1-norm minimization.Experimental results indicate that the proposed method is more effective and robust than the existing methods based on l1norm minimization.

object tracking;sparse representation;l1minimization;meta-sample;principal component analysis

format：ZHANG Ying，FAN Ya-xiang，SUN Hao，et al.Object Tracking Algorithm Based on Sparse Representation for Meta-sample［J］.Journal of Chongqing University of Technology：Natural Science，2014(1)：91 －95.

TP391

A

1674－8425(2014)01－0091－05

10.3969/j.issn.1674－8425(z).2014.01.018

2013－07－20

国防科学技术大学优秀学位论文选题资助项目

张英(1984—)，男，陕西彬县人，硕士研究生，主要从事计算机视觉与智能信息处理研究。

张英，樊亚翔，孙浩，等.基于元样本稀疏表示的目标跟踪算法［J］.重庆理工大学学报：自然科学版，2014(1)：91 －95.

(责任编辑 杨黎丽)