基于SiCp/6061Al复合材料二维真实微观结构的简化模型

中北大学机电工程学院 李超 原梅妮 李立州 郎贤忠

前言

颗粒增强金属基复合材料（MMC）由于具有高的比强度、比刚度及良好的耐磨性、热稳定性等优点，目前已经成功被应用于航空航天、汽车及体育器材等领域[1]。金属基复合材料的力学性能及损伤破坏规律取决于复合材料的微观结构特征，而复合材料的真实微观结构往往具有的结构复杂、计算量大等特点，致使研究人员多采用简化模型以及单胞模型的方法进行有限元仿真和计算。虽然这些方法在很大程度上降低了计算量，有利于颗粒增强金属基复合材料力学特性的规律总结与开发利用，但不同模型中由于增强颗粒的不同形状、局部密度、体积分数等因素，均会对金属基体的流动性、颗粒的约束能力、颗粒与基体的接触面积以及颗粒的转动造成不同程度的影响，使得计算结果和真实情况产生一定的偏差[2]。

本文以SiCp/Al复合材料的微观电镜图为基础，建立了含有颗粒真实形状的微观模型。以此模型为基础，建立了含有相同颗粒体积分数、体积与坐标的多种简化模型。使用了子模型技术对不同模型进行有限元建模和计算，通过对比不同模拟的计算结果与云图，验证不同模型的有效性。

1 模型建立

1.1 材料参数

在复合材料的有限元模型中，S i C颗粒为线弹性，其弹性模量Ep=440 GPa，泊松比νp=0.17。6061铝为具有各向同性的弹塑体，其弹性模量为EAl=70 GPa，泊松比νAl=0.33[3]。基体的弹塑性应力—应变关系满足Ludwik硬化法则[4]：

其中，σY和εp分别表示流变应力和塑性应变，表示屈服应力，h和n分别表示硬化系数与硬化指数。与6061铝相对应的参数为[5]：

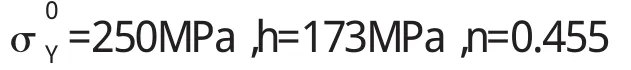
1.2 CAD模型

本文使用的SiC p/6061 Al复合材料，其颗粒体积分数为15%。以复合材料的S E M图为基础，通过设置适当的阈值等参数，对S E M图像中的像素进行逐一识别，生成如图1所示的C A D模型，在此定义为原始模型。

图1 CAD模型（原始模型）的建立过程

1.3 多种简化模型的建立

本文使用的简化模型包括三种：圆形颗粒、正四边形颗粒、正六边形颗粒。首先以原始模型为基础，在不改变模型中单个颗粒的面积和形心位置的情况下，将颗粒形状分别转化为相应的简化形状。经过初步转化，一些靠近边缘的颗粒会与模型边界相交，为保证模型中颗粒位置的随机性不变，将其与内部较小的颗粒进行位置交换。最终，得出了与原始模型具有相同颗粒密度和随机性的三种简化模型。其转化结果如图2所示。

图2 不同颗粒形状的简化模型

1.4 网格划分与边界条件

如图3所示，将原始模型以子模型的形式嵌入到尺寸远大于原始模型的宏观模型当中，模型均使用CPE3（3节点线形平面应变三角形单元）的单元类型进行网格划分。通过对宏观模型进行单向拉伸模拟，研究子模型的材料特性，及原始模型和三种包含不同颗粒形状的简化模型。

图3 模型的边界条件与网格划分

2 结果与讨论

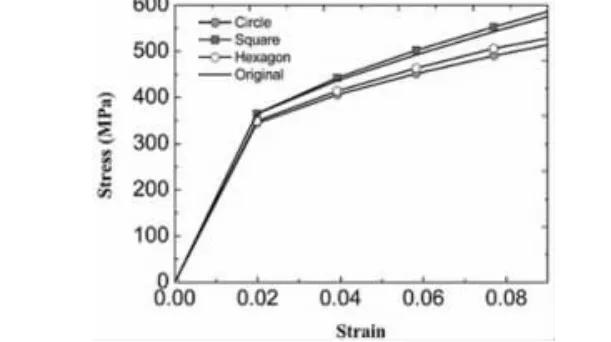
图4 不同形状颗粒模型的应力-应变曲线

如图4为含有不同颗粒形状模型的应力-应变曲线。图中，它们在弹性阶段几乎重合，并且具有着非常相似的应变硬化和应变率硬化趋势。可以看出，颗粒形状的改变，并没有对复合材料的弹性参数有所影响。而在材料的应变硬化阶段，发现圆形颗粒与正六边形颗粒模型的预测应力较低，而正四边形颗粒模型的预测应力最大并略高于原始模型。

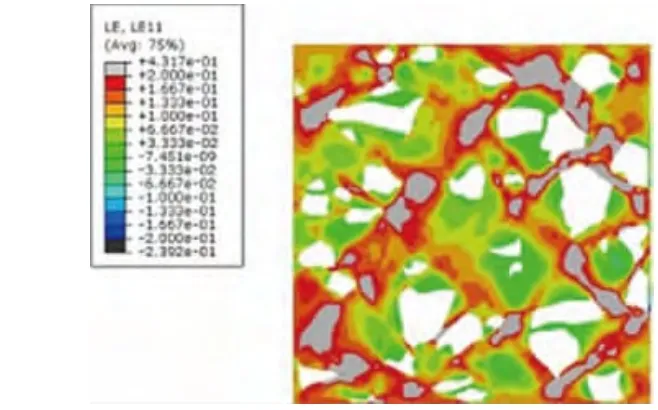
图5 原始模型的应变云图

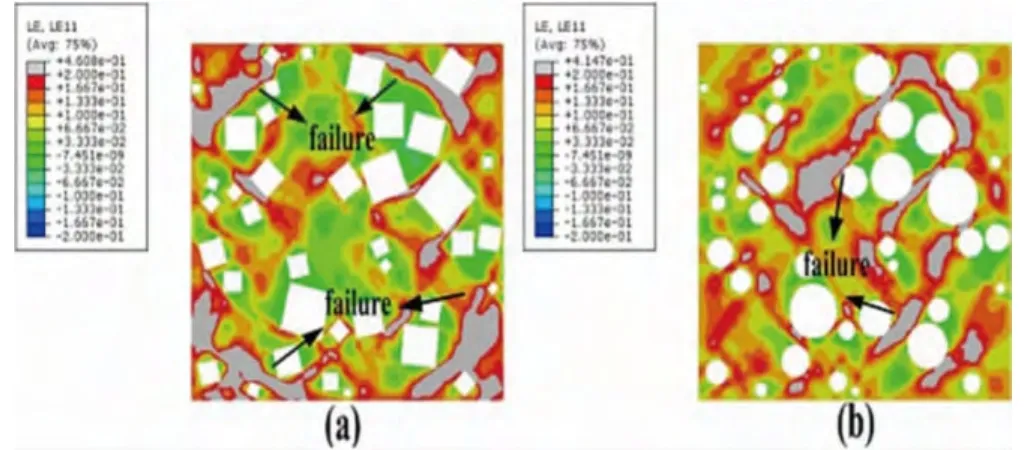
图6 包含正方形颗粒与圆形颗粒模型的应变云图

通过对比，如图5、图6所示三种模型发现，模型中均显示出了沿加载45°方向较大的塑性变形带，但含有正四边形颗粒模型中的失效区域（灰色区域）要明显多于圆形颗粒模型，并且在所有模型中均可发现，模型中的失效区域多集中于颗粒棱角处以及颗粒较为密集的区域。而从含有正四边形颗粒的简化模型与原始模型对比看出，原始模型中基体的应变分布则显得更为均匀。

规律总结得出，通过使用圆形、正六边形等较为圆滑的简化颗粒模型对复合材料进行有限元模拟计算，其计算结果准确度较低，这是由于该种简化模型中颗粒与基体的接触面积较小，以及圆滑的颗粒形状使得金属基体有着相对较高的流动性，造成颗粒对基体的约束能力降低，颗粒能够吸收的应力减少，因而表现出的增强效果较原始模型会有所降低，但值得关注的是其因此产生的应变分布的均匀性以及较低的应变损伤。虽然具备棱角要求的正四边形颗粒表现出的增强效果、失效面积均与原始模型较为接近，但含正四边形颗粒的模型中基体的应变分布较原始模型相比，其失效区域则显得的较为集中，这是由于正四边形相对于原始的不规则形状，其棱角过于尖锐，应力集中现象过于明显造成的。

3 结论

3.1 形状圆滑的简化模型，会使模拟结果在各方面均存有较大误差，而类似于正四边形的含有棱角的简化模型，其模拟的应力-应变曲线虽然与原始模型较为接近，但其应变分布情况与原始模型仍然存有较大误差。

3.2 由于不同颗粒形状的简化模型对SiCp/Al复合材料的弹性参数没有影响并且其表现出的应变硬化和应变率硬化趋势较为相似，该方法在研究颗粒密度、分布情况对复合材料力学性能的影响、规律总结上能够起到简化模型的作用，但在精确计算参数等方面，其不具有可行性。

[1]Yuan M N, Yang Y Q, Li C et al. Numericalanalysis of the stress-strain distributions in the particle reinforcedmetal matrix composite SiC/6064Al [J]. Materials and Design,2012, 38∶1～6.

[2]原梅妮,杨延清,李茂华等.金属基复合材料多尺度计算方法研究进展[J]. 材料导报,2012 年,26(9)∶134～137.

[3]Zhang P, Li F G. Microstructure-based Simulation ofPlastic Deformation Behavior of SiC Particle Reinfored AlMatrix Composites, Chinese Journal of Aeronautics[J], 2009, 22∶663～669.

[4]L.L. Mishnaevsky Jr. Three-dimenisonal numbericaltesting of microstructures of particle reinforced composites [J],Acta Materialia, 2006, 52(14)∶4177～4188.

[5]Wang J C, The simulation of damping capacity ofSiCp/Al composites [D]. Northwestern Ploytechnical University,1991.