基于改进DLMS算法的自适应FIR滤波器设计

2014-01-22 11:01邱陈辉徐祖强

计算机工程与设计 2014年3期

李锋，邱陈辉，徐祖强

（江苏科技大学电子信息学院，江苏镇江212003）

0 引言

基于LMS算法的时域自适应滤波器被广泛应用于通信、雷达、声呐、地震学和生物医学工程等领域，主要分成系统辨识、逆模型，预测，干扰消除四大类别［1，2］。虽然已经有前人对基于FPGA芯片和LMS算法的自适应滤波器做了研究探讨，但是机械地将理论算法映射到系统芯片上，或者采用Simulink搭建模块群再使用DSP Builder转换成VHDL/Verilog程序来实现自适应滤波器都不是最佳方案，前者不能充分发挥理论算法的真正优势，后者导致程序的极大冗余性，显然对自适应滤波器的处理速度和FPGA的资源利用率是不利的。本文首先回顾自适应滤波结构和算法，然后提出改进的DLMS算法，并使用MATLAB对其进行仿真验证，接着在FPGA上选用FIR直接型结构实现该自适应滤波器，并且采用流水线技术进行优化，最后将其与先前的设计方案进行对比给出结论。

1 自适应滤波器的结构和算法

严格意义上讲，自适应滤波器是时变的、非线性的，但若滤波器输出端滤波、平滑或预测的量是它的输入观测量的线性函数，我们往往认为该滤波器是线性的。线性自适应滤波器的实现分成结构和算法两部分。前者根据自适应滤波器的脉冲响应是否有限长可以分为有限长脉冲响应（FIR）和无限长脉冲响应（IIR）结构，FIR结构由于只具有前向路径而更受青睐，它又可以细分为直接型、转置型、网格型和脉动阵列型［1］。本文采用最直观的、应用最广泛的FIR直接型结构。

Bernard Widrow等人于1960年提出的LMS算法由最速下降法推导出来，基于维纳滤波理论和最小均方误差（MMSE）准则，属于线性自适应滤波算法。

令x（n）＝［x（n），x（n－1），…，x（n－L＋1）］T表示自适应滤波器的输入信号矢量，其中L表示该滤波器的阶数，w（n）＝［w0（n），w1（n），…，wL－1（n）］T表示抽头权值矢量，d（n）表示期望信号，用于给最优滤波提供一个参考，y（n）表示该滤波器的输出信号，e（n）表示误差信号，则LMS算法的基本形式如下：

滤波输出

估计误差

抽头权值更新

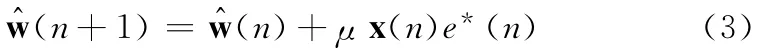
其中H表示转置和共轭相结合的埃尔米特转置，＊表示共轭，＾表示对权值系数当前值得估计。μ表示LMS算法的收敛因子，也叫步长参数，尽管［1，2］详细推导并给出了μ的取值范围，然而其上限涉及输入矢量x（n）的自相关矩阵的最大特征值，下限仅要求大于零，但在实际应用中非但该最大特征值难以求解，而且取接近零的正值仍可能导致自适应系统的不稳定，因此μ值的最终确定通常需要进行反复试验。该算法的结构图十分直观，如图1所示。

图1 LMS算法的结构

上述表达式是LMS算法的复数形式，实数形式只需将埃尔米特转置 “H”改成普通转置 “T”；而e（n）的共轭就是其本身，“＊”可以去掉；抽头权矢量的当前值我们认为就是其当前估计值， “＾”亦可去掉。虽然该算法用最速下降法推导出来，需要求均方误差函数的梯度，并且涉及输入矢量的自相关矩阵，但是最终的算法形式不需要进行平方、求均值、求微分等复杂运算，仅需要乘法和加减运算［2，3］。可幸的是，乘法和加减运算是所有运算中最容易用硬件实现的，并且FPGA芯片嵌入了较多硬线加减器和乘法器的参数化模块LPM＿add＿sub、LPM＿mult，这让加减、乘法运算运算的速度提高许多［4］。所以本文选用LMS及其改进算法，无疑对实时信号的处理速度大有裨益。

2 改进的DLMS算法

查看式（3）不难发现，要获取w（n＋1）必须先知道当前时刻的误差信号e（n），即先要完成式（2）的运算才能进行式（3）的计算。显然，抽头权值的更新不能和滤波输出同时进行。尽管LMS算法的计算复杂度不高，但这种严格执行顺序抑制了该算法的运行速度。再者，实现LMS算法的自适应滤波器最宜采用FIR直接型结构，但是此结构的关键路径比较长，并且LMS算法实质上是非线性的，同时包含前向路径和反馈路径［5］，所以无法直接采用流水线技术对其进行速度优化。

为此，Guozhu Long等人在1989年提出了延迟最小均方（DLMS）算法。这种算法只在抽头权值更新过程中引入一个延迟D，利用延迟的误差信号与输入向量的乘积来更新抽头权值，相当于将式（3）的迭代结构分成多个周期计算，式（3）变成如下形式

该算法引入的延迟是对整个自适应滤波系统的延迟，所以滤波输出的延迟也是D周期。尽管Long等人证明了当延迟量小于自适应滤波器的阶数时，DLMS算法的敛散性没有太大的影响，但是延迟量越大必然对该算法的收敛性能影响越大，并且影响滤波输出的速度［6，7］。因此本文提出了改进的DLMS算法：在自适应滤波器的权值更新路径中引入延迟m1，又在滤波输出路径中引入延迟m2，本算法的结构图如图2所示。

图2 改进的DLMS算法结构

对照图1可以看出，图2将滤波输出和期望信号减去滤波输出这两部分合并到了误差计算模块；在权值自适应更新过程中，估计误差被延迟了m1周期，输入信号也被延迟了m1周期，与此同时滤波计算过程用到的抽头权值延迟m2周期。这样滤波输出得延迟时间被有效地减少到m2周期［8］。这里式（1）～式（3）变为

滤波输出

估计误差

抽头权值更新

值得一提，当输入信号、期望信号的位宽不变，并且自适应滤波器的阶数很小，而m1和m2不论怎样取值，该自适应滤波器的收敛性都不太理想时，我们可以尝试将μ值适量减小。

下面采用正弦信号sin（0.125πt）t∈［1，1024］作为自适应滤波器的期望信号，将零均值、单位方差的高斯白噪声以SNR＝5掺入上述正弦信号作为输入信号，分别对4阶基于LMS算法和改进DLMS算法的自适应滤波器进行仿真，相应结果分别如图3～图6所示。

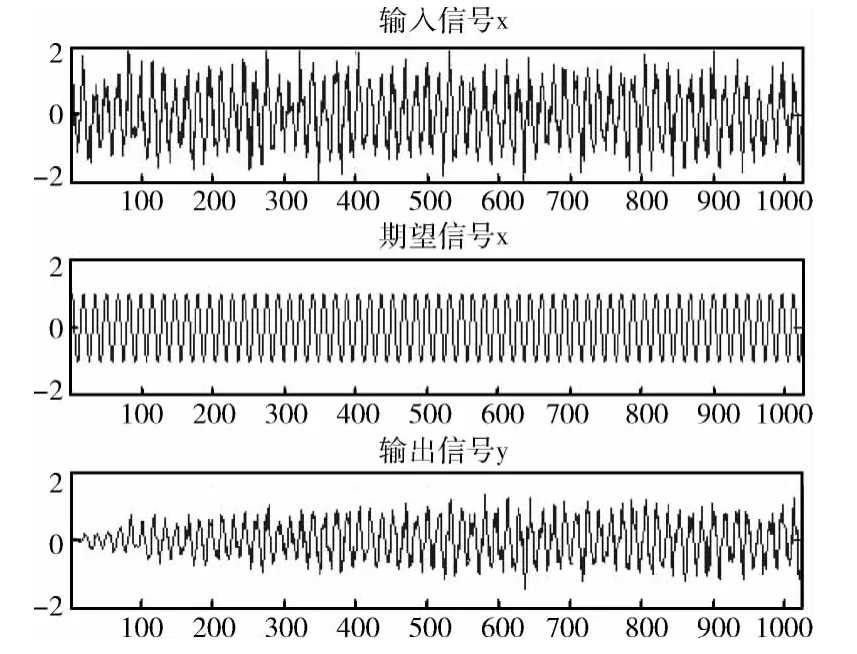
图3 采用LMS算法各个信号波形

图4 采用LMS算法的权值自适应

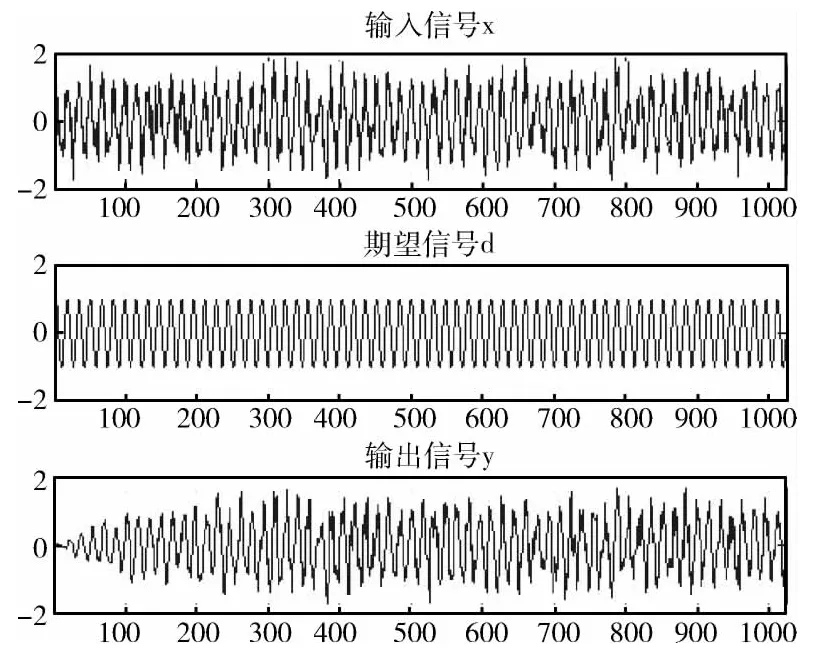
图5 采用改进DLMS算法各个信号波形

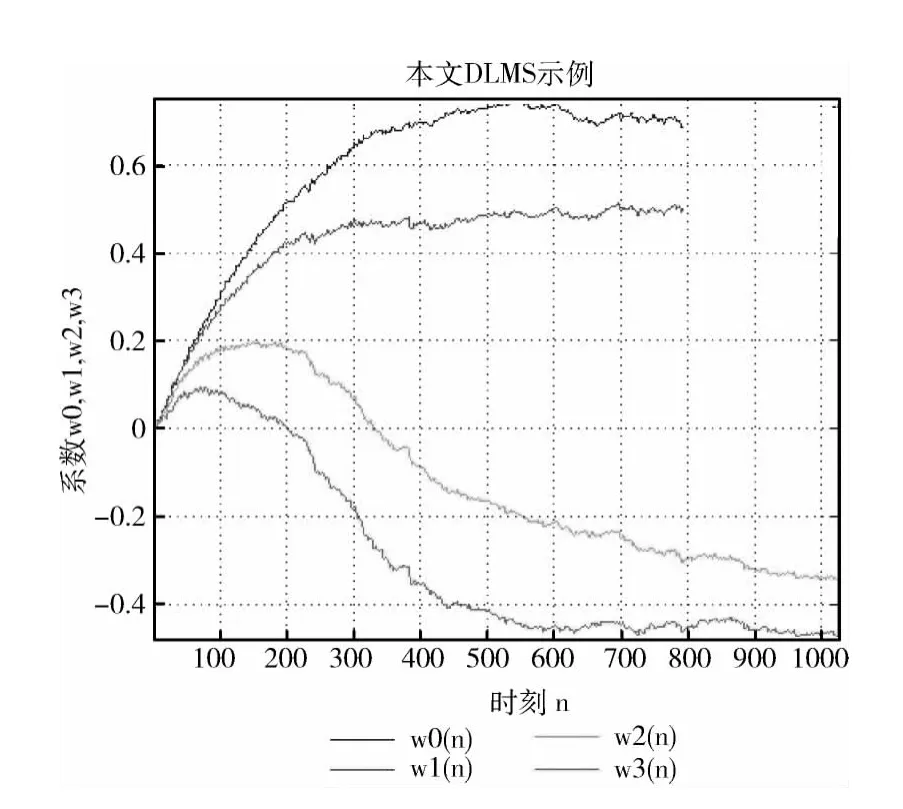
图6 采用改进DLMS算法的权值自适应

图3和图5分别是采用LMS和改进DLMS算法的自适应滤波器的输入信号、期望信号和输出信号的波形图，前两者对应相同，输出信号波形亦大体相似，都是从零开始变化且慢慢平缓，但改进DLMS算法的输出信号变化较为剧烈。图4和图6中自适应滤波器的4个抽头权值总体更新走势相似，但采用改进DLMS算法的自适应滤波器的4个权值波动相对大些。这是由于改进DLMS算法的收敛性能严格意义上不如LMS算法，但其收敛性通常也能很好地满足实际应用的要求。此外，两种算法中y（n）和d（n）的差别都较为明显，如果增大自适应滤波器的阶数，则其差别明显减小。但是阶数越高，自适应滤波器的实现成本越大，并且运行速度也会放缓。因此实际应用中须慎重选择合适的阶数。

3 基于FPGA实现

FPGA主要依靠并行化提高处理速度，如何将一个理论上顺序执行或者说串行的算法高效地映射到FPGA芯片上是当前的热门话题。流水线技术是最常用的并行化技术之一。它将延时较大的组合逻辑块切割成两块延时大致相等的组合逻辑块，从而显著提高设计的运行速度上限。事实上，加入流水线并不会减少原来设计中的总延时，甚至增加插入寄存器的延时和信号同步的时间差，但它却可以提高总体的运行速度［4，9］。

由于LMS算法存在反馈路径，并且严格顺序执行，不能采用一般流水线技术进行优化。而采用改进DLMS算法的自适应FIR滤波器的权值更新路径和滤波输出路径中都加入了延迟，在FPGA实现时都相应添加了锁存器，并且基于FPGA的自适应FIR滤波器的输入、输出、抽头权值都要进行截断处理来保证固定位宽［10］，因此，在采用改进DLMS算法的自适应FIR滤波器的前向路径中可以采用流水线技术对乘法运算进行优化。对乘法结果的累加运算（sum of product，SOP）一般利用加法树实现，这里的累加运算也可以用流水线技术进行优化［11］，但是该优化不需要我们特地编程设计，在高版本的Quartus II集成开发软件对HDL程序进行编译综合时将自动进行。

本文使用VHDL对采用LMS算法和改进DLMS算法的自适应FIR滤波器进行编程描述，在Altera公司Cyclone III系列的EP3C10U256C8芯片上实现，用到了内置嵌入式乘法器模块。以设计4阶自适应FIR滤波器为例，取定输入信号、期望信号、抽头权值的位宽为8位；误差信号和输出信号的位宽为16位；为了将例中的乘法器全部流水线化，流水线级数设为6级；设定延迟量m1＝3，m2＝3。所有信号都采用二进制补码形式表示，采用有符号的十进制形式显示。输入信号、期望信号的数值是通过将第三节最后仿真时所使用的输入信号、期望信号经由MATLAB量化得到的。图7和图8分别给出了采用LMS算法和改进DLMS算法的时序波形图，时钟clk的周期设置为100ns，占空比设置为50%。

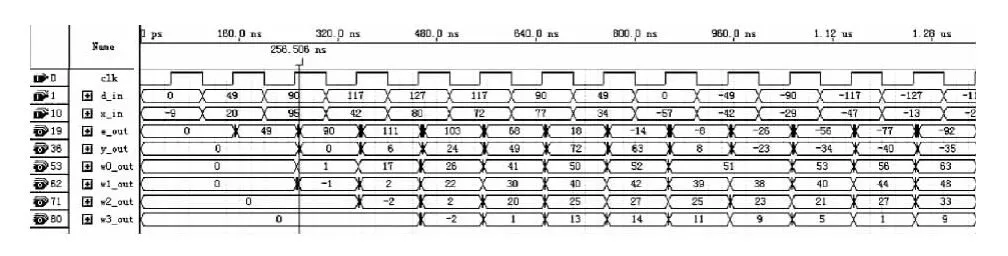
图7 采用LMS算法的自适应FIR滤波器时序波形

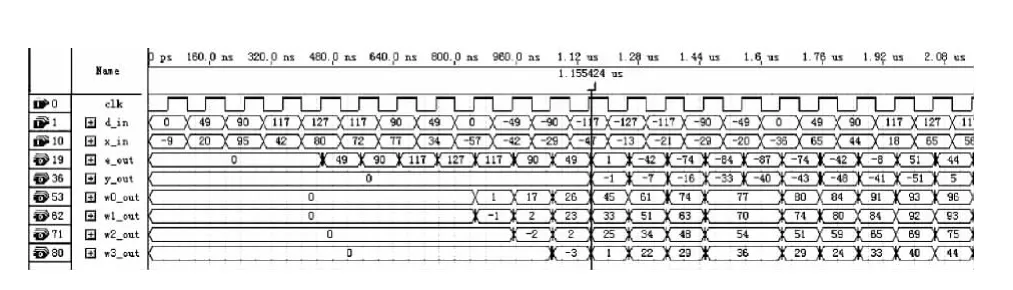
图8 采用改进DLMS算法的自适应FIR滤波器时序波形

结合图7－图8可以看出，采用LMS算法的自适应FIR滤波器的初始延迟时间比采用改进DLMS算法的自适应FIR滤波器的初始延迟时间短一些，但是总体运行速度后者要比前者快许多，表1所列的Fmax或者叫做Registered Performance证实了这一点。后者的初始延迟时间较长主要因为在其RTL电路中多加了6个锁存器。由于篇幅所限本文只给出最开始的时序波形，其实越往后两种算法所设计的自适应FIR滤波器的4个抽头权值的更新都越平缓，并且后者相对 “摆动”剧烈一点，这与第三节MATLAB仿真结果是吻合的。表1给出采用两种算法时分别消耗的资源和运行的速度。

表1 基于两种算法的自适应滤波器所耗资源和速度比较

4 结束语

本文首先简述LMS算法，并在此基础上提出改进的DLMS算法，接着分别使用这两种算法结合FIR直接型结构设计出自适应滤波器。在MATLAB上仿真成功后就在FPGA硬件上进行时序验证。在采用改进DLMS算法设计实现时还利用流水线技术对其乘法器进行优化。两种验证结果总体上都满足要求。由表1知本方案的处理速度虽然提高到原先设计的2倍多，但它所消耗的FPGA硬件资源也比原先增加了一倍多。这印证了硬件设计中速度和资源的永恒矛盾：要想节省资源必然降低处理速度，而要想提高速度必定消耗更多资源。所以在工程应用中要根据实际需求进行取舍或折中。

［1］Simon Haykin.Adaptive filter theory ［M］.ZHENG Baoyu，transl.Beijing：Publishing House of Electronics Industry，2010：159－238 （in Chinese）.［Simon Haykin.自适应滤波器原理［M］.郑宝玉，译.北京：电子工业出版社，2010：159－238.］

［2］Bernard Widrow，Samuel D Stearns.Adaptive signal processing ［M］.WANG Yongde，LONG Xianhui，transl.Beijing：China Machine Press，2008：68－76 （in Chinese）. ［Bernard Widrow，Samuel D Stearns.自适应信号处理［M］.王永德，龙宪惠，译.北京：机械工业出版社，2008：68－76.］

［3］LI Ning.Convergence performance analysis and applications of adaptive LMS algorithm ［D］.Harbin：Harbin Engineering University，2009：15－52 （in Chinese）.［李宁.LMS自适应滤波算法的收敛性能研究和应用［D］.哈尔滨：哈尔滨工程大学，2009：15－52.］

［4］PAN Song，HUANG Jiye，PAN Ming.EDA practical tutorial Verilog HDL ［M］.Beijing：Science Press，2010：27－56 （in Chinese）.［潘松，黄继业，潘明.EDA技术实用教程－Verilog HDL ［M］.北京：科学出版社，2010：27－56.］

［5］Meher P K，Chandrasekaran S，Amira A.FPGA realization of FIR filters by efficient and flexible systemization using distribu－ted arithmetic ［J］.IEEE Trans Signal Processing，2008，56（7）：3009－3017.

［6］Guo Rui，Linda S DeBrunner.Two high－performance adaptive filter implementation schemes using distributed arithmetic ［J］.IEEE Transactions on Circuits and Systems－II：Express Briefs，2011，58 （9）：600－604.

［7］Meher P K，Sang Yoon Park.High－throughput pipelined realization of adaptive FIR filter based on distributed arithmetic［C］//IEEE 19th International Conference on VLSI and System－on－Chip，2011：428－433.

［8］Meher P K，Sang Yoon Park.A high－speed FIR adaptive filter architecture using a modified delayed LMS algorithm ［C］//IEEE International Symposium on Circuits and Systems，2011：121－124.

［9］YANG Haigang，SUN Jiabin，WANG Wei.An overview to FPGA device design technologies ［J］.Journal of Electronics and Information Technology，2010，32 （3）：714－723 （in Chinese）.［杨海钢，孙嘉斌，王慰.FPGA器件设计技术发展综述［J］.电子与信息学报，2010，32 （3）：714－723.］

［10］GAO Yajun.Digital signal processing based on FPGA ［M］.Beijing：Publishing House of Electronics Industry，2012：79－104（in Chinese）. ［高亚军.基于FPGA的数字信号处理［M］.北京：电子工业出版社，2012：79－104.］