基于ANSYSWorkbench的斩波轮支架模态分析

于海辉，景 晨，黑丽民

（公安部第一研究所，北京 100048）

0 引言

斩波轮的工作转速为1500r/min，回转直径达700mm，通过支架与整机连接。因此支架结构在工作中承受着复杂的外力作用，为保证斩波轮旋转时整机系统具有较好的性能，避免支架因斩波轮旋转产生共振，造成对机器的破坏，有必要对斩波轮支架进行模态分析。ANSYS Workbench 是专业的有限元分析软件[1]，通过分析斩波轮支架的模态，为支架的结构设计提供参考。

1 模态分析的基本理论

模态分析是将线性定常系统振动微分方程中的理论物理坐标变换为模态坐标，并将耦合方程变为非耦合方程组，该方程组以模态为参数，然后求解出模态参数。坐标变换中的变换矩阵为模态矩阵，其各列就是模态振型。

斩波轮支架是一个多自由度振动系统，其振动作用力方程为[2]：

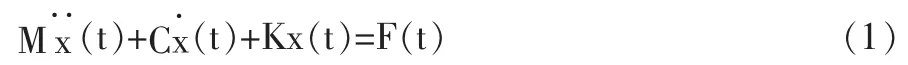
斩波轮支架自身的阻尼矩阵C 很小，可以忽略其影响。当激振力矩阵F（t）=0 时，为系统的自由振动，而系统的固有频率和主振型是振动系统的固有属性，因此通过求解无阻尼自由振动的方式来研究系统的振动固有频率和主振型，即：

求解式（2）得到固有频率和主振型方程为：

其中，A 为主振型，即模态振型；ωn为系统的固有频率。要使式（3）有解，则：

由式（4）知，n 个自由度振动系统方程有n 个特征值，即有n 个固有频率，将特征值代入方程（3），即可得到相应的模态振型。

利用有限元分析软件Workbench 对该结构进行模态分析时，实质是将该支架结构在静止状态下进行人为激振，然后用模态分析理论通过对函数的曲线拟合，识别出结构的模态参数，从而建立起结构的模态模型。根据模态叠加原理，在已知各种载荷时间历程的情况下，就可以预言结构实际振动的响应历程或响应谱。基于该理论，使用Workbench 进行有限元分析，得到斩波轮支架的各阶模态和振型云图。

2 斩波轮支架有限元模型建立

斩波轮支架结构复杂，因此使用Pro/E 建立装配几何模型，如图1 所示，然后利用其与Workbench 的接口直接导入进行分析。Workbench 与三维建模软件有多种接口方式，本文使用Pro/E 5.0 与ANSYSWorkbench 14.0对接，模型不需要中间格式转换，直接将asm 格式的Pro/E 模型导入分析。

有限元计算是基于节点进行的，而节点又与网格单元息息相关，Workbench 的网格划分是智能化的，在生成网格的过程中，精度要求较高的区域会自动调节网格密度，保证整个系统的网格质量[3,4]。

在Workbench 的Analysis Systems 工具栏中选择Modal 分析模块，材料选用Q235B 结构钢，在导入模型之后进行网格划分，并选取网格设置工具Sizing 中的Element Size 为10mm，即网格单元尺寸为10mm，节点总数为61235 个，单元总数为17343 个。为便于网格划分，将连接螺纹孔去掉，优化后的网格划分模型如图2 所示。

图1 斩波轮支架模型Fig.1 The model of Chopper wheel bracket

图2 网格模型Fig.2 The mesh model

3 斩波轮支架的模态分析

模态分析就是要确定斩波轮支架的振动特性，得到支架固有频率和振型的计算过程。该斩波轮支架的前十一阶模态分析结果见图3。

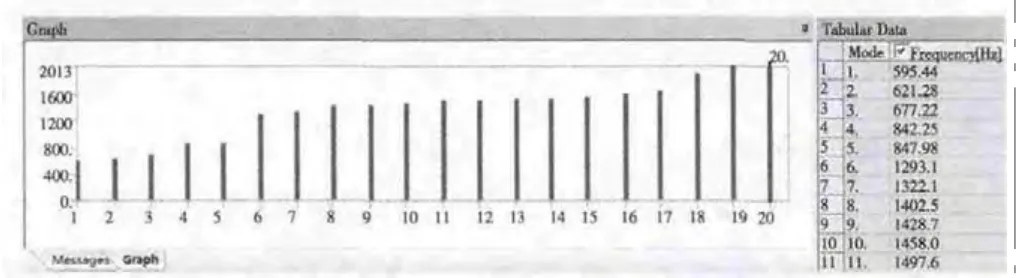
图3 前十一阶模态固有频率Fig.3 The modal frequency of eleven order

通过模态计算结果可知，斩波轮支架前11 阶的固有频率在595.44～1497.6Hz 范围内，振型主要是弯曲、扭转和弯扭组合，其中支架的一阶模态为1 阶扭转振型，二阶模态为2 阶扭转振型，三阶模态为1 阶弯扭组合振型，四阶模态为2 阶弯扭组合振型，五阶模态为1 阶垂直弯曲振型，六阶模态为1 阶水平弯曲振型，前六阶模态振型如图4 所示。

图4 支座的前六阶振型云图Fig.4 The modal images of six order bracket

4 结论

一阶固有频率为595.44Hz，对应斩波轮的临界转速为35726.4r/min，而斩波轮的工作转速为1500r/min，临界转速远大于斩波轮工作转速，系统在工作过程中不会产生共振。斩波轮的工作频率远离各阶固有频率，证明本文斩波轮支架的结构设计具有足够的刚度和强度，在工作转速范围内不会产生共振，能够很好的实现承载斩波轮工作并与整机连接的功能。

[1] 张元通.基于ANSYS WORKBENCH 的颗粒机机架的模态分析[J].信息技术，2011，2.

[2] 闻邦春，刘树英，张纯宇.机械振动学（第2 版）[M].北京：冶金工业出版社，2011.

[3]张功学，田杨. 基于ANSYS Workbench 的变速自行车车架的有限元分析[J].信息化纵横，2009，6.

[4] 司豪杰，田哲文，梅小明，邝勇.基于Workbench 的客车车身骨架模态分析[J].北京汽车，2013，4.