GPS控制网严密平差及精度评定研究

杨胜辉

(贵州中水建设管理股份有限公司，贵阳550001)

GPS控制网严密平差及精度评定研究

杨胜辉

(贵州中水建设管理股份有限公司，贵阳550001)

GPS测量技术与传统测量技术相比具有诸多优越性，无论在工程还是导航上，其用与高精度的特点都已成为共识并使这项技术得到广泛运用。文章阐述了GPS控制网严密平差及精度评定，并提出了消除系统误差影响的措施。

GPS;控制网;平差;计算;误差;精度

1 GPS控制网平差

1.1 GPS网平差的目的

在GPS网的数据处理过程中，基线解算所得到的基线向量仅能确定GPS网的几何形状，但却无法提供最终确定网中点的绝对坐标所必需的绝对位置基准。在GPS网平差中，通过起算点坐标可以达到引入绝对基准的目的。不过，这不是GPS网平差的唯一目的。总结起来，进行GPS网平差的目的主要有3个:①消除由观测量和已知条件中所存在的误差而引起的GPS网在几何上的不一致。②改善GPS网的质量，评定GPS网精度。通过网平差，可得出一系列可用于评估GPS网精度的指标，结合这些精度指标，还可以设法确定出可能存在粗差或质量不佳的观测值，并对它们进行相应的处理，从而达到改善网的质量的目的。③确定GPS网中点在指定参照系下的坐标以及其他所需参数的估值。在网平差过程中，通过引入起算数据，如已知点、已知边长、已知方向等，可最终确定出点在指定参照系下的坐标及其他一些参数，如基准转换参数等。

1.2 GPS网平差计算

包括:①在进行控制测量王的平差计算时，必须采用可靠以及严密的计算软件对其进行计算，利用非同步观测的控制网基线向量作为观测到的数值，并且使用地面水平方向作为横坐标，利用三维严密平差的方法对平差进行有效的计算。②如GPS D级网平差时将市区GPS C级控制网点作为起算的固定点，采用三维严密约束平差方法进行平差计算，获得坐标系成果。将GPS基础控制网点作为起算的固定点，通过计算得出坐标系的成果。③将控制网平差计算出来之后，就需要对控制网的精度以及计算进行严格的控制。

2 平差精度

2.1 高程控制网严密平差及精度评定

高程精度主要与相邻两排高程控制点之间的跨距(平均基线长为单位)有关。最大标准误差和平均高程误差大体上与这个跨距成正比例地变化。根据控制网中所观测到的数据等情况，利用平差的函数模型对其的准确定进行验算。

2.1.1 水准网的条件平差

步骤:①根据实际问题，确定条件方程的个数(等于多余观测的个数)，列出改正数条件方程。②组成法方程式(等于条件方程的个数)。③解算法方程，求出联系数k。④将k代入改正数方程求出改正数v，并计算平差值。⑤计算单位权中误差。⑥将平差值代入平差值条件方程式，检核平差值计算的正确性［1］。

2.1.2 水准网的间接平差

步骤:①将条件平差的方程、改正数条件方程以及法方程列出。②将观测得到的平差值以及高程平差值计算出来。③对观测平差值以及高程平差值的精度进行判断和确定。④最后利用平差模型对其准确性进行检验。

2.1.3 高程精度结论

对于由20%的旁向重叠的航摄像片所构成的区域，至少要有3排高程控制点分别布设在区域的首末两端和中央。区域网的高程精度主要取决于相邻两排高程控制点之间的跨距(以平均基线长为单位表示)。随着跨距的增加，高程误差将成正比地增大。在跨距较短(i≤5)的条件下，区域网的高程精度可以保持在单位权中误差的数量级。大体相当于0.1%的航高。如果区域的范围太大，则在区域的内部应该布置多排高程控制点。使用60%旁向重叠的航摄像片，能够提高平差区域的理论高程精度，并且可以采用格网状的布点方案。由于最大的高程误差总是出现在区域的上下两条边缘航带、相邻两排高程控制点的中间部位，所以，在这些地方增补一个高程控制点，可以有效地提高区域网的高程精度，并改善精度分布的均匀性。

2.2 平面控制网(导线网)严密平差及精度评定

2.2.1 条件平差

步骤:①根据实际问题，确定条件方程的个数(等于多余观测的个数)，列出改正数条件方程。②组成法方程式(等于条件方程的个数)。③解算法方程，求出联系数k。④将k代入改正数方程求出改正数v，并计算平差值。⑤计算单位权中误差。⑥将平差值代入平差值条件方程式，检核平差值计算的正确性。

2.2.2 边角网的间接平差

边角网的间接平差步骤与水准网的间接平差步骤相同，之后就需要对最弱点误差椭圆参数进行计算，对点位误差椭圆进行绘制，然后将该点至已知点的边长平差值中误差、方位角平差值中误差求出来。

2.2.3 平面精度的主要结论

对于平面区域网平差而言，只要有周边控制就够了。区域内部的控制点可以局部改善精度，但不能代替周边控制。在具有密集周边控制的条件下，区域网的平面精度与区域大小几乎无关，且整个区域内精度的分布是十分均匀的。在具有密集周边控制的条件下，区域的形状是无关紧要的。在具有稀疏周边控制的条件下，最大标准误差总是出现在区域边缘上两个相邻控制点的中央地带。区域网的平面精度大体与控制点之间的距离成线性关系。使用60%的旁向重叠的航片，大约可以提高精度40%。

3 测量平差的函数模型

在GPS测量工作中，对模型的建立主要包含了通过测量工作对某些几何量的大小进行确定的数量问题。但是控制测量网所观测到的数值是一个随机的变量，因而在进行模型的建立时，是与其他数学模型是有所不同的，需要考虑的因素非常多。常见的平差函数模型有条件平差法、附有参数的条件平差、间接平差法(参数平差法)、附有限制条件的间接平差等。

在前面所学到的基本平差方法中，可以知道最基本的数据就是观测值向量，进行平差时除建立其函数模型外，还要同时考虑到它的随机模型，亦即观测向量的协方差阵:

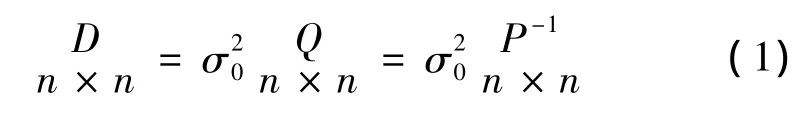
式中:D为L的协方差阵;Q为L的协因数阵;P为L的权阵，为单位权方差。函数模型连同随机模型，就称为平差的数学模型。在进行平差计算前，函数模型和随机模型必须首先被确定，前者按上面介绍的方法建立，后者须知道P、Q、D其中之一。

求得D的估值。

4 消除系统误差影响的措施

①在区域网的平差之前，通过摄影机检定的办法，求出其存在的系统误差，而在量测的像点坐标中加以改正。②在平差过程中，使用扩充了的数学模型，用附加的参数来抵偿各种系统误差的联合影响。这些附加参数作为待定参数在整体平差的过程中确定。人们称这种方法为自检校法。由于这种方法不要求知道任何系统误差的具体形式，也不要求增加任何附加观测，所以得到了广泛地采纳。③在平差之后，采用某种内插方法，根据已知地面控制点上的残余误差，对平差结果加以调整改正。这种方法叫做区域网的外部平差。

［1］王岩.高精度施工控制网平差系统的研究与开发［D］.南京:河海大学，2005.

P228.4

B

1007－7596(2014)07－0195－02

2013－12－13

杨胜辉(1986－)，男，苗族，贵州施秉人，助理工程师，从事水利工程测量工作。