一类线性方程组解的条件与求解

陈 静

(扬州职业大学，江苏 扬州 225009)

循环矩阵是一类应用非常广泛的特殊矩阵，它具有许多特殊而良好的性质和结构，对其有关问题的研究显得很有必要.文献［1-4］研究了求循环矩阵的逆与广义逆的快速算法.在现代科技工程中，常遇到以循环矩阵为系数矩阵的线性方程组的求解问题，文献［5］利用多项式理论给出系数矩阵为麟状因子循环矩阵的线性方程组的解的条件与求解的快速算法，它更利于计算机实现，也利于并行计算.受此启发，本文给出系数矩阵为结式循环矩阵的线性方程组解的判定条件和求解方法.

1 定义与引理

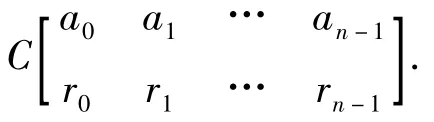
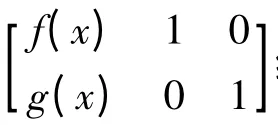
定义2［7］A∈Cn×n，若存在B∈Cn×n，使得(1)ABA=A，(2)BAB =B，则称B 为A 的反射g 逆，记为A(1，2).若只满足条件(1)，则称B 为A 的一个{1}-逆.

由文献［7］可知，Ax=b 有解时，有AA(1，2)b=b.

引理4［7］设B 为m×n 矩阵A 的一个{1}-逆，若线性方程组Ax=b 有解，则其通解为x=Bb+(I-BA)Z，Z 为任意的n 维列向量.

2 主要结果

定理1 结式循环矩阵线性方程组Ax=b 有唯一解的充要条件为(f(x)，g(x))=1.当结式循环矩阵线性方程组Ax=b 有唯一解时，存在唯一的结式循环矩阵T，使得T 的第一列为Ax=b 的唯一解.

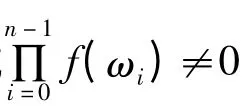
设b=(b0，b1，…，bn-1)T，以b 为第一列构造一结式循环矩阵经过行初等变换一定可化为

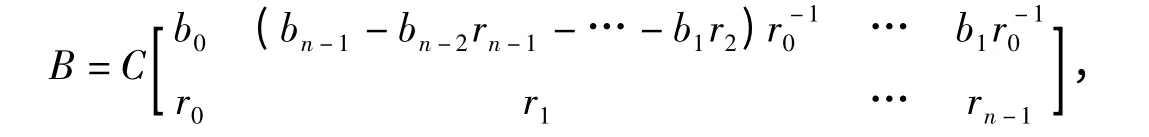
于是，u(x)f(x)+v(x)g(x)=1，u(x)h(x)=c(x)，u(P)A=I，u(P)B =c(P).若取T=c(P)=A-1B，则T 的第一列为A-1b，且AA-1b =b.所以T 的第一列为结式循环矩阵线性方程组Ax =b 的解.由于A-1和B 唯一均为结式循环矩阵，所以T 为结式循环矩阵且唯一，从而A-1b 是Ax=b 的唯一解.

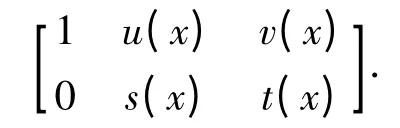
则u(x)f(x)+v(x)g(x)=1，u(P)A=I，故A 可逆，从而结式循环矩阵线性方程组Ax=b 有唯一解.

定理2 设g(x)无重根，则结式循环矩阵线性方程组Ax =b 有无穷多解的充要条件为(f(x)，g(x))≠1，且AA(1，2)b=b。当结式循环矩阵线性方程组Ax=b 有无穷多解时，存在结式循环矩阵H 及C，使得C 的第一列X1为Ax=b 的一个特解，X=X1+(I-H)Z 为Ax=b 的通解，Z 为任意的n 维列向量.

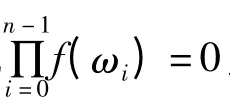
设(f(x)，g(x))=d(x)≠1，且设f(x)=d(x)f1(x)，g(x)=d(x)g1(x)，则(f1(x)，g1(x))=1，由于g(x)无重根，所以(d(x)，g1(x))=1，从而(f(x)，g1(x))=1，(f(x)d(x)，g1(x))=1.

设b=(b0，b1，…，bn-1)T，以b 为第一列构造一结式循环矩阵

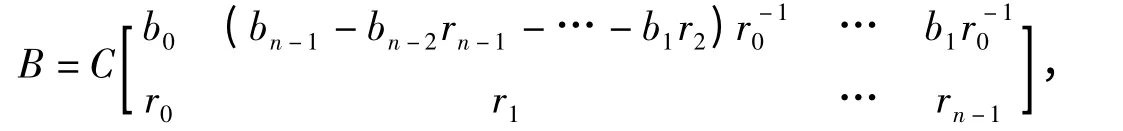
且设B 的表征多项式为h(x).多项式矩阵

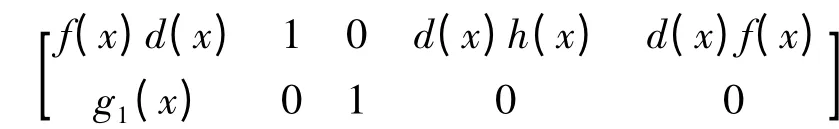
经过一系列初等行变换可化为

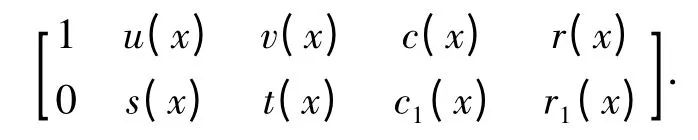
于是 f(x)d(x)u(x)+g1(x)v(x)=1，d(x)u(x)h(x)=c(x)，d(x)u(x)f(x)=r(x).

由f(x)d(x)u(x)+g1(x)v(x)=1 得

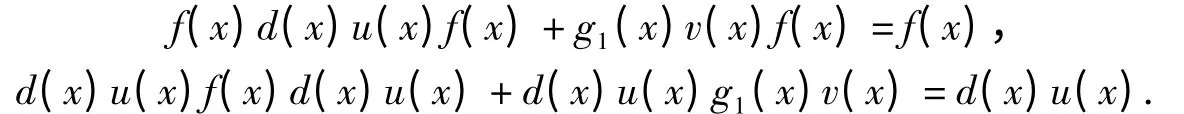
若令T=d(P)u(P)，C=c(P)，H=r(P)，则ATA =A，TAT =T，C =TB，H =TA，且T，C，H 均为结式循环矩阵.由ATA=A，TAT=T 可知T=A(1，2).因为C 的第一列为Tb，且ATb =AA(1，2)b =b，所以C 的第一列Tb 为Ax=b 的一个特解.又A［Tb+(I-H)Z］=b+AZ-AHZ=b+AZ-ATAZ=b，故X=X1+(IH)Z 为Ax=b 的通解，Z 为任意的n 维列向量.

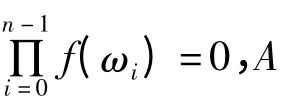
3 算法与算例

根据定理1 和定理2 的证明，不难得到求结式循环矩阵线性方程组Ax=b 解的方法，其步骤如下:

(1)求多项式f(x)，g(x)，h(x)及矩阵P;

(3)若d(x)=1，则T=c(P)的第一列即为Ax=b 的唯一解;

(4)若d(x)≠1，设g(x)=d(x)g1(x)，利用行初等变换化多项式矩阵

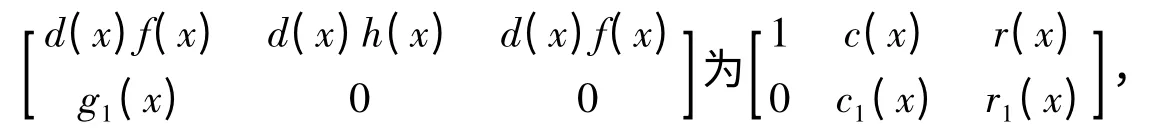
则C=c(P)的第一列为Ax=b 的一个特解X1，X=X1+(I -H)Z 为Ax =b 的通解，H =r(P)，Z 为任意的n 维列向量.

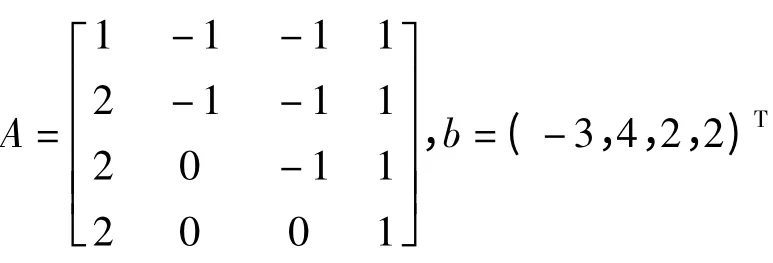
例1 已知，解线性方程组Ax=b.

解 由定义可知

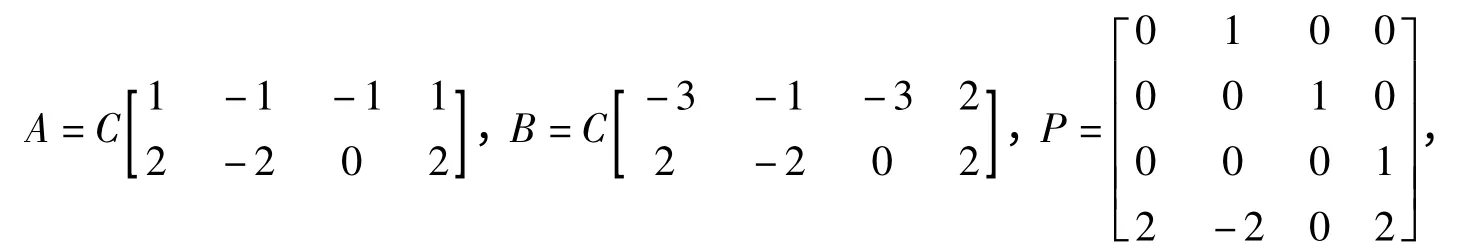
故 f(x)=1 -x-x2+x3，g(x)= -2 +2x-2x3+x4，h(x)= -3 -x-3x2+2x3.

因此 c(x)=3 -2x+2x2-5x3+2x4，从而

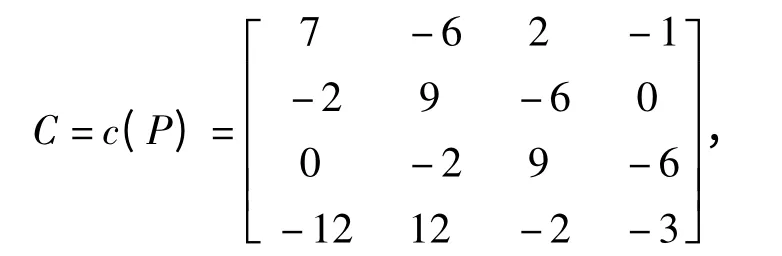
所以原方程组的唯一解为(7，-2，0，-12)T.

故 f(x)=1 -2x+x2，g(x)=1 -x-x2+x3，h(x)=2 -4x+2x2.显然(f(x)，g(x))=d(x)=f(x)=(x-1)2，g1(x)= -x-1.

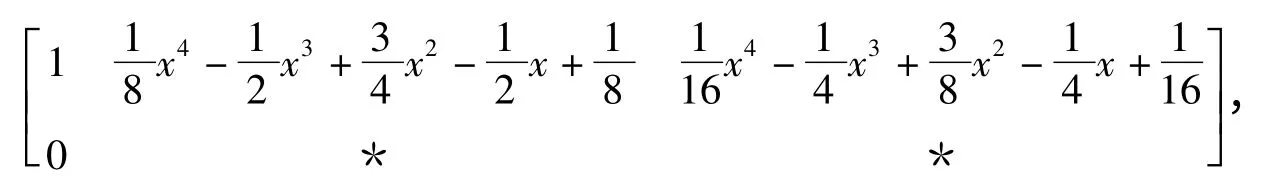
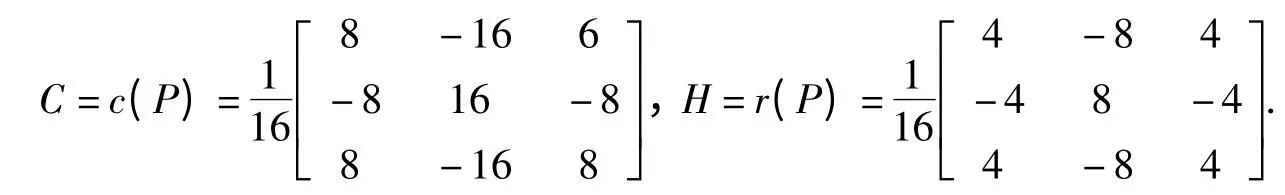
［1］ 贾瑞娟，杨学桢，张志海.结式循环矩阵的逆与广义逆［J］.系统工程理论与实践，1997(11):124 -129.

［2］ 江兆林，刘三阳，张圣贵.求置换因子循环矩阵的逆阵及广义逆阵的快速算法［J］.高等学校计算数学学报，2003，25(4):227 -234.

［3］ 何承源，胡明.关于两类循环矩阵求逆的一种快速算法［J］.数值计算与计算机应用，1998(4):258 -2264.

［4］ 刘桂香，许乃武.求结式循环矩阵的逆与广义逆的快速算法［J］.扬州教育学院学报，2005，23(3):6 -9.

［5］ 何承源，罗新建，胡明.鳞状因子循环矩阵方程解的条件与求解的快速算法［J］.工程数学学报，2007，24(3):519 -526.

［6］ 张小红，蔡秉衡.高等代数专题研究选编［M］.西安:西安科学技术出版社，1992.

［7］ 陈永林.广义逆矩阵的理论与方法［M］.南京:南京师范大学出版社，2005.