薄冲积层下开采地表动态移动规律与特征

唐 君，王金安，王 磊

（北京科技大学 金属矿山安全高效开采教育部重点实验室，北京 100083）

1 引 言

我国自南水北调、西气东输、西电东送建设开始后，对高压线、输气管线、河流等穿越采煤影响区问题日益突出。国内外对采煤引起的岩层及地表移动规律有了较深刻地认识，例如，国外Barry 等[1]对地下采矿引起的地表下沉类型及其机制进行了比较系统地研究。国内王金庄等[2]，刘林[3]，余学义等[4]对巨厚岩层下开采进行研究，得出地表沉陷是由上覆基岩和松散层双层介质作用所致，并且地表移动具有初始期、活跃期短而衰退期较长等特点；郑志刚等[5]，滕永海等[6]，谭志祥等[7]对综采放顶煤开采进行研究，得出此方式下开采地表移动剧烈、下沉盆地陡峭、移动变形集中、导水断裂带异常发育，具体表现为地表下沉系数、主要影响角正切明显偏大等；黄平路等[8]对复杂地质条件下矿山开采进行研究，得出在采矿之初，地表塌陷主要是由地下水疏干引起的；地表大规模塌陷形成以后，地下采空区的扩大是引起地表塌陷的主要原因，但矿区特殊的地质条件对地表塌陷范围的扩展速度有重要影响；刘玉成等[9]对煤层埋深与厚度之比较大情况下的地表沉降进行研究，得出在形成矩形采空区的过程中，由上覆岩层移动形成地表下沉盆地的形态和大小主要取决于离地表最近一层主关键岩层的弯曲，且地表的下沉量远远小于关键层岩层厚度的观点。由此可见，地层条件是矿山开采岩层移动的基础，决定着地表塌陷的类型与过程。现如今国内外对薄冲积层下采煤引起的岩层及地表移动的研究尚不充分，特别是地表下沉及变形的动态机制研究有待深入。

天祝煤矿位于甘肃省天祝藏族自治县炭山岭镇，此地区地层有元古界、中生界、新生界3 层，中生界侏罗纪中统窑街组（J2Y）为本区主要含煤地层。煤系地层走向一般为北10°～40°西，倾向北东，倾角一般为9°～18°之间；含煤总层数为4 层，平均总厚度为9.94 m，可采煤层2 层：上层煤及中层煤，局部可采煤层一层（顶层煤）。其中3229 工作面倾斜长度为140 m，走向长度为1 368 m，煤层开采厚度为6.32 m，平均采深为360 m。值得注意的是，本区第四系覆盖层较薄，仅为12 m，主要由表土、冲积砾石及堆积碎石构成（见图1），并且地表有金沙河流过，3229 工作面距金沙河最近水平距离只有180 m 左右（见图2）。

众所周知，地下开采造成覆岩及地表自下而上形成三带，即：垮落带、导水裂缝带和弯曲下沉带[10]，弯曲下沉带主要由第四系冲积层构成，当冲积层较薄时，地表移动变形将会导致导水裂隙带通达至地表。为防止金沙河水沿采动裂隙倒灌到井下，给工作面生产和安全构成严重威胁，文献[11]对该区地下开采覆岩裂隙发育高度进行了分析，文献[12]提出了金沙河防渗四元结构，该结构自下而上依次为：河床加固层、防渗垫层、防渗层及保护层。其中，加固层提高河床强度，减轻因地下采动对河床的影响，保证河床的整体性；防渗垫层防止因河床错动或砾石对防渗层的折损，同时可协调和吸收部分河床局部变形；防渗层主要进行防渗，并具有足够的厚度、强度、耐寒、耐热及耐紫外线老化性能；防渗保护层防止防渗层直接与水面接触，有固定防渗层、保护防渗层的功能，同时还起到维护河床生态的效果。然而，地表移动变形是一个动态发展过程，防渗结构设计应适应地表动态变形发展。因此，迫切需要对金沙河附近采动影响下的岩层与地表开展动态移动规律研究。这不仅为评价河床防渗工程可靠性提供依据，更为薄冲积层矿区安全开采提供了理论和实践基础。

图1 岩层柱状图Fig.1 Rock strata histogram

2 观测站布置

为观测地表动态岩移规律与特征，在3229 工作面分别沿工作面走向和倾向布置了两条观测线。走向观测线上设置了22个测点，编号分别是Z0、Z1、…Z22；倾向观测线设立了19个测点，编号分别是Q0、Q1、…Q19。测线上各测点间距25 m。3229 工作面地面岩移观测测点布置如图2 所示。

3229 工作面2011年7 月14 日初采，至2012年11 月16 日开采结束，期间每月均采用DTM352C全站仪监测地表移动变形，共进行了16 次观测。观测期全面覆盖并反映了采动地表移动变形规律及特征。

（1）走向方向，随着工作面远离，工作面后方地表下沉趋势逐渐趋于稳定，下沉量逐渐增加，最大下沉点随工作面推进向前推移。当工作面开采1 000 m时，采空区内地表累计最大下沉量为1 493 mm，达到最终总下沉量的98%。随后地表下沉逐渐趋于稳定（见图3（a））。地表水平移动基本是朝向工作面推进方向，当工作面开采长度小于1 000 m时，地表水平移动有逐月增加的趋势，之后地表移动逐渐趋于稳定（见图3（b））。

（2）倾向方向，随着工作面的推进，地表下沉量逐渐增加，最大沉陷区域始终处于采空区上方。当工作面开采1 000 m 后，地表下沉逐渐趋于稳定，最终为1 523 mm。金沙河附近下沉量始终较小，累计下沉量为8 mm（见图3（c））。地表水平移动基本是朝向采空区方向，当工作面开采长度小于1 000 m时，地表水平移动有逐月增加的趋势，最大水平移动点位于工作面下山侧外缘35 m 左右，之后随着工作面的推进，地表水平移动逐渐趋于稳定。金沙河附近水平移动较小，最大水平位移仅为-19.27 mm、7.89 mm（见图3（d））。

图2 监测点平面布置图Fig.2 Layout of measurement point

图3 实测地表移动变形图Fig.3 Surface movement and deformation curves by in-situ measurement

3 沿走向方向地表动态移动变形特征与规律

地下开采引起的地表沉陷和移动变形是一个复杂的时间和空间过程。为了掌握随工作面开采沿走向方向地表移动和变形的时空变化规律，对工作面走向测线监测数据进行动态分析，得到沿走向方向地表动态移动变形Knothe 函数特征以及地表移动动态参数和轨迹。

3.1 地表移动变形动态特征与改进的Knothe时间函数

地表沉陷随时间的发展过程可以分为3个阶段，即地表下沉的初始阶段、发展阶段和衰减阶段[13-14]。地表下沉的初始阶段下沉量增长缓慢，下沉速度增加较快，而地表下沉到发展阶段时，地表下沉量会有大幅增长，且增长速度逐渐达到最大。而地表下沉的衰减阶段沉陷变形曲线形态基本不再变化，下沉量会继续增加，但增加缓慢，并且此阶段下沉速度逐渐减小最终趋近于0。因此，下沉量动态曲线应呈现为大致的S 型曲线，下沉速度曲线类似于正态分布曲线。

现场地表岩移监测走向测线上的Z0点，即倾向测线上的Q2点为测线布置范围内最终下沉量最大点（见图3）。图4(a)中显示此点地表下沉量及下沉速度随工作面推进的动态变化特征。工作面开采距此点110 m 左右时，地表点开始进入活跃期，但下沉量始终较小。当工作面推过该点30 m 后，地表下沉量急剧增加。当工作面推进到过该点50 m左右时，地表下沉进入剧烈期。当工作面推过该点88 m时，该点的下沉速度达到最大，为20.6 mm/d，地表点移动最剧烈，之后逐渐减小。当工作面推过该点150 m 左右时，剧烈期结束。当工作面推过该点400 m 左右时活跃期结束，此后地表点进入衰退阶段，地表沉降逐渐趋于稳定，沉降速度逐渐趋近于0。由此可见，薄冲积层下综采放顶煤开采地表移动初始期很短,活跃期比较长（历时185 d），地表点的下沉量达到该点总下沉量的90.7%，而剧烈期较为显著，但时间相对较短（历时约60 d）。

对薄冲积层下开采地表走向测线上水平移动、变形最大点进行研究发现，其移动变形曲线随工作面推进也大致为S 型，并且当工作面未推至到此点时，地表移动变形较小，地表点水平加速往复运动，并出现小幅的拉伸变形。当工作面推进至此点50 m范围内时，地表开始向开采工作面方向产生倾斜变形。当工作面开采过该点后，地表开始向采空区内加速移动并且同期开始产生大幅倾斜变形，地表进入活跃期。当工作面推进到过该点200 m时，地表水平移动变形速度与倾斜速度同时达到最大，最大水平移动速度为3.92 mm/d，最大水平变形速度为0.059 mm/m/d，最大倾斜变形速度为0.118 mm/m/d。当工作面推进到过该测点300 m 后，地表水平移动变形呈现震荡衰减趋势，当工作面推进到过该点600 m（约350 d）时，地表点水平移动变形仍出现小幅增加，而倾斜变形有所减小。地表整个变形过程中剧烈期非常显著，工作面推进引起的地表水平移动变形相对于倾斜变形更为敏感（见图4(b)、(c)、(d)）。

图4 沿走向地表动态移动变形曲线Fig.4 Dynamic movement and deformation curves of surface along strike of coal seam

1952年波兰学者Knothe[15]利用土压实的基本假设进行了地表移动与变形时间过程研究，认为地表下沉速率dW(t)/dt与地表最终下沉值W0和某一时刻t 的动态下沉值W(t)之差成比例，即

式中：c为与上覆岩层力学性质有关的时间因素影响系数，其单位为1/a。

根据初始时刻边界条件：t=0，W(t)=0，对式（1）积分，可得

式（2）就是Knothe 地表移动动态过程的下沉表达式[16-17]。但Knothe时间函数所描述的地表下沉是一个逐渐衰减的过程，不能反映地表下沉全程变化特征。针对Knothe时间函数的不完整性，文献[18]和[19]在原时间函数模型式（2）上加一个幂指数k，将其改为如下的形式：

式中：k为待拟合参数。

由于工作面监测与开采同时进行，因此，地表下沉变形与工作面推进距离的关系更为紧密。同时，工作面基本为匀速推进，下沉曲线整体为S 型，借鉴改进的Knothe时间函数，设定拟合曲线函数为

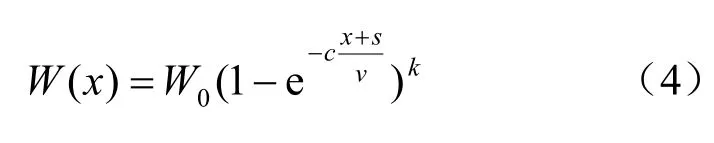
式中：x为测点距工作面的距离；s为监测点到工作面切眼相对距离；v为平均开采速度。

将地表下沉最大点的相关参数W0=1 523 mm，s=483.7 m，v=2.93 m/d，代入式（4），并对图4(a)地表下沉量随工作面推进的变化曲线进行拟合，得到拟合系数c=0.035，k=1 145.24，R2=0.998 6。

薄冲积层下开采走向测线其他监测点均为S 型下沉曲线。并且受地表工作面开采制度和开采沉降时间等因素的影响，距离开切眼越远地表沉降越充分，地表下沉曲线S 型越明显（见图5）。将其相关参数代入式（4），对图5 地表下沉量随工作面推进的变化曲线进行拟合，得到拟合系数见表1，由R2数值看拟合效果较好。

对改进的Knothe时间函数式（3），对时间t求一阶导数得出下沉速度V 表达式[17]：

图5 沿走向地表移动变形曲线Fig.5 Movement and deformation curves of surface along strike of coal seam

表1 沿走向地表移动各测点下沉曲线拟合参数Table 1 Fitted parameters of ground subsidence along strike of coal seam

同理，基于工作面基本为匀速推进，设定下沉速度拟合曲线函数为

代入上述地表下沉量拟合系数，可得到该点下沉速度随工作面推进变化的拟合曲线与现场监测数据基本吻合，其中最大下沉点速度拟合曲线如图4(a)所示。

由于走向测线地表最大移动变形点变形曲线类似于下沉曲线，大致为S 型（见图4），基于薄冲积层开采沉降拟合公式（4），提出地表移动变形拟合公式为

式中：y为监测点移动变形值；y0为监测点最终移动变形值。

根据现场实测数据，拟合得到走向测线移动变形最大点拟合系数（见表2），拟合曲线如图4(b)、(c)、(d)所示，拟合效果较好。

表2 沿走向地表移动变形曲线拟合参数表Table 2 Fitted parameters of ground movement and deformation along strike of coal seam

在走向测线上，地表水平移动、变形曲线均具有S 型特征，并且随着工作面开采地表测点S 型特征趋于明显，如图5 所示。将各监测点相关参数代入式（7）进行拟合，得到其拟合参数（见表3～5），总体拟合效果较好。Z7之后的局部监测点由于地表本身移动变形量较小，未达到充分采动，因而测量误差对结果本身影响相对较大，测量误差导致曲线S 型特征不明显。因此，没有进行拟合。

3.2 地表起动距与超前影响角

起动距反映工作面开采对地表岩移的初始开采长度。实测结果表明，薄冲积层下3229 工作面开采起动距为139.7 m，约为采深（H0）的0.39 倍。符合我国一般在初次采动时起动距为(1/4～1/2)H0的变化范围[20]。

表3 沿走向地表各测点水平移动曲线拟合参数Table 3 Fitted parameters of ground horizontal displacement along strike of coal seam

表4 沿走向地表各测点水平变形曲线拟合参数Table 4 Fitted parameters of ground horizontal deformation along strike of coal seam

表5 沿走向地表各测点倾斜变形曲线拟合参数Table 5 Fitted parameters of ground inclination along strike of coal seam

超前影响角大小受采动程度、工作面推进速度和上覆岩层岩性等因素的影响。据实测，该工作面刚开采时地表下沉基本处在采空区正上方，地表下沉传播超前影响范围较小，随工作面推进，超前影响范围稍有增大。当工作面开采400 m 左右后，影响角最终约为80°（见图6）。分析认为，薄冲积层条件下，当开采深度较大、开采速度达到或超过某一定值时，由于距离和时间的影响，地下开采对地表前方产生沉降的影响传播较弱。因此超前影响范围较小，即停采前塌陷盆地始终位于开采工作面的上方附近。

图6 超前影响角示意图Fig.6 Schematic of pre-influence angle

3.3 地表测点移动轨迹

地表点从开始移动到剧烈移动，再到逐渐停止，是一个较为复杂的时间、空间过程。根据走向测线测点下沉及水平移动监测数据，捕捉到薄冲积层下开采走向测线地表测点移动轨迹（见图7）。地表移动变形初期，地表水平方向主要是向工作面前方移动，并产生一定的下沉量。随着工作面开采，地表开始向工作面后方移动，并迅速产生大量沉降。之后大部分时间是在采空区范围内往复运动。除此以外，沿着工作面推移方向测点从Z17～Z1（见图2），地表移动轨迹逐渐趋于简单化、规律化，分析认为主要是由于初始开采时，地表移动范围影响不到Z1点所致。

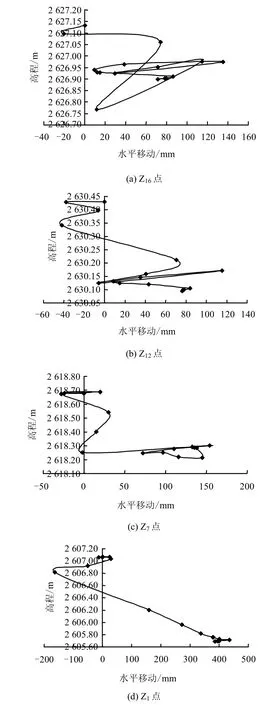
图7 地表移动轨迹图Fig.7 Trajectories of surface movement

4 地表沿倾向方向动态移动变形特征与规律

通过对工作面倾向测线监测数据计算，分析薄冲积层下开采的3229 工作面对金沙河附近地表影响范围和程度，结果表明，沿倾向方向地表动态移动变形同样符合Knothe 函数特征，地表移动角满足指数函数动态特征。

4.1 地表移动变形动态特征与改进的Knothe时间函数

对薄冲积层下开采地表沿倾向测线上水平移动、变形最大点进行研究发现，当工作面未推进至此点时，地表移动变形较小。当工作面推进至距此点60 m 范围内时，地表产生小幅倾斜变形，之后随着工作面推进，地表开始水平移动变形。当工作面开采过该点后，地表首先向采空区内加速倾斜变形，之后迅速开始产生大幅水平移动变形，地表进入活跃期。当工作面推进过该点88 m时，地表倾斜变形速度首先迅速达到最大为0.26 mm/m/d；工作面再向前推进90 m时，地表水平变形速度也达到最大为0.10 mm/m/d。当工作面推进到过该点300 m 后，地表点移动变形逐渐趋于稳定。地表整个变形过程中剧烈期非常显著，水平变形速度增减呈阶梯状，且地表倾斜变形相比于水平移动变形更为敏感（见图8）。

倾向测线移动变形最大点变形曲线呈S 型，符合改进的Knothe时间函数，依照式（4）和式（7）对薄冲积层下开采倾向地表移动变形曲线进行拟合，获得拟合系数见表6，拟合曲线见图8。由R2数值看，拟合效果很好。

薄冲积层下开采，倾向测线其它测点下沉曲线S 型规律明显，并且随着监测点距离工作面中心逐渐接近，地表最终沉降逐渐变大，S 型曲线趋于拉伸化、稳定化。在水平方向上，地表移动变形曲线类似于走向测点移动变形曲线，呈S 型或倒S 型，如图9 所示。依照式（4）和式（7）进行拟合，拟合结果见表7～10，拟合效果较好。

图8 沿倾向地表移动变形曲线Fig.8 Dynamic movement and deformation curves of surface along inclination of coal seam

图9 沿倾向地表移动变形曲线Fig.9 Movement and deformation curves of surface along inclination of coal seam

参照地表下沉速度拟合公式（6）的形式，得出地表移动变形速度拟合公式为

将地表移动变形拟合系数代入式（6）和式（8），得到地表移动变形速度随工作面推进变化规律，与现场实测数据总体变化趋势相同，拟合程度较高，基本符合上式。其中，最大移动变形点速度拟合曲线见图8。

表6 沿倾向地表移动变形曲线拟合参数表Table 6 Fitted parameters of ground movement and deformation along inclination of coal seam

表7 沿倾向地表各测点下沉曲线拟合参数表Table 7 Fitted parameters of ground subsidence along inclination of coal seam

表8 沿倾向地表各测点水平移动曲线拟合参数Table 8 Fitted parameters of ground horizontal displacement along inclination of coal seam

表9 沿倾向地表各测点水平变形曲线拟合参数Table 9 Fitted parameters of ground horizontal deformation along inclination of coal seam

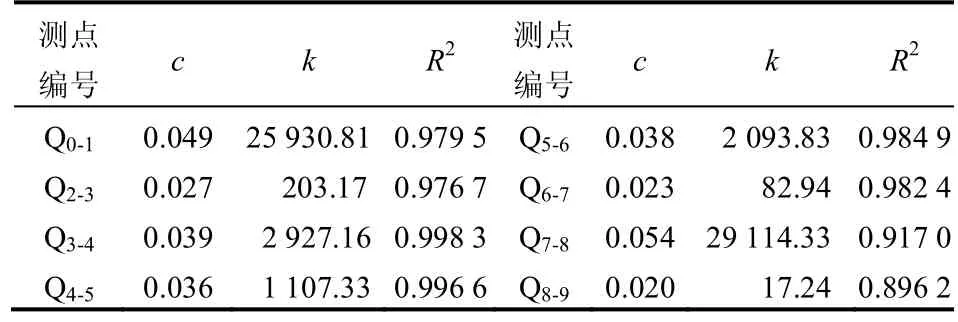
表10 沿倾向地表各测点倾斜变形曲线拟合参数Table 10 Fitted parameters of ground inclination along inclination of coal seam

4.2 移动角动态变化规律

薄冲积层开采地表下山移动角变化规律如图10 所示。随着工作面逐渐开采，地表下山移动角逐渐减小。在工作面未推进到倾向测线时，下山移动角以0.75°/m 速度减小，当开采到其下方时，移动角未有改变，当工作面推过该测线时，移动角以0.1°/m 速度减小，并于工作面推过倾向侧线500 m左右后趋于稳定，其值在60°左右。下山移动角总体动态变化趋势可用下式表述：

式中：β为下山移动角；a,b,d为待拟合参数。

拟合得到相关系数a=19.236 7，b=172.058 11，d=59.934 2，拟合曲线如图10 所示。

图10 地表下山移动角变化趋势图Fig.10 Trends of moving angle towards down inclination

5 地表裂缝观测分析

地表变形最直接的后果就是使地表产生裂缝或错动，导致河水倒灌到井下，易造成淹井事故，给工作面生产和安全构成严重威胁。裂缝宽度则与岩土体性质有关。

现场勘测发现，工作面开采600 m 左右后，首次在走向和倾向测线附近发现裂缝，如图11 所示。在走向方向距工作面后方214 m 处，发现倾向裂缝（图中裂缝1），宽度为0.03 m，长度为6 m。之后随工作面采动裂缝暂无发展。在倾向方向，距金沙河往西60～210 m 范围内，发现走向沉陷裂缝（图中裂缝2～6），裂缝宽度在0.01～0.05 m 之间。裂缝2～4为裂缝密集区，裂缝长度3～100 m 不等。随工作面开采裂缝向南发育，密集区向东有小范围扩大，裂缝长度增长100%～233%。

图11 现场地表裂缝发展位置图Fig.11 Locations of surface cracks

薄冲积层条件下，由于开采深度较大，开采制度较完善，因此，工作面走向方向地表水平变形控制在一定范围内，产生的走向裂缝较少。而在倾向测线方向，随着工作面开采，地表从采空区到金沙河附近产生了不均匀沉降及水平移动，且水平变形较大，因此，产生的倾向裂缝较多，并且裂缝随工作面开采逐渐发育。

应当指出，文献[12]提出的柔性四元防渗结构为开放式梯形断面，对于平行裂缝有良好的吸收和防御作用。并且薄冲积层下开采产生的地表最大移动变形发生在采空区附近，金沙河附近移动变形相对较小，截止到开采完毕，金沙河最大水平位移仅为-19.27 mm、7.89 mm，最大水平压缩变形为0.605 mm/m，最大拉伸变形为0.8 mm/m。在湿润的条件下，四元防渗结构的防渗层土工膜径向的拉伸强度为217.8 kN/m，并且经向断裂伸长率为288%，纬向断裂伸长率为123%，可见，文献[12]提出的柔性四元防渗结构能够满足协调和缓冲开采扰动河床变形的要求。

6 结 论

（1）实测表明，薄冲积层下放顶煤开采地表下沉移动初始期很短；活跃期比较长（历时185 d），地表点的下沉量达到该点总下沉量的90.7%；剧烈期较为显著，最大下沉速度达20.6 mm/d，但剧烈扰动时间相对较短（历时约60 d）。所有测点下沉曲线均为S 型分布，下沉速度曲线类似为正态分布，参考Knothe时间函数，地表下沉量曲线可表达为式（4）；下沉速度曲线为式（6），拟合结果与现场实测数据相符。

（2）薄冲积层下开采，在工作面未推进到达时，地表移动变形较小；工作面开采后，地表迅速进入活跃期，并且速度达到最大；当工作面推进到过300 m 后，地表点移动变形逐渐趋于稳定。整个地表移动变形过程中剧烈期非常显著，并且走向测线地表水平移动变形对工作面的推进更为敏感，倾向测线地表则为倾斜变形更为敏感。其中，充分采动的测点移动变形值满足式（7）函数。

（3）沿着工作面推进方向，初始开采时地表初始变形阶段主要朝向回采工作面前方做水平和下沉移动，之后大部分时间是在采空区范围内往复运动。总体来说，地表点移动是一个较为复杂的时间、空间过程，在采空区上方表现出移动轨迹的简单化和规律化。

（4）研究得出薄冲积层放顶煤开采地表移动动态参数。其中，起动距为139.7 m，约为0.39H0。超前影响角80°，超前影响范围偏小。随着工作面逐渐开采，地表下山移动角逐渐减小，其值最终稳定于60°，变化规律满足曲线式（9）。

（5）薄冲积层下开采，平行于工作面走向方向的地表裂缝更易发育。随着工作面推进，地表裂缝前移，密集区向工作面外侧有小范围扩大，裂缝沿工作面走向长度发育较快。

就天祝煤矿金沙河床防渗工程而言，设计的柔性四元防渗结构[12]可以适应工作面采后地表剧烈变形期的变形速率且满足移动变形的要求。

[1]BARRY H G B,BROWN E T.Rock mechanics for underground mining[M].London:George Allen Unwin,1985.

[2]王金庄,李永树,周雄,等.巨厚松散层下采煤地表移动规律的研究[J].煤炭学报,1997,22(1):18-21.WANG Jin-zhuang,LI Yong-shu,ZHOU Xiong,et al.Ground movement cause by mining under thick alluvium[J].Journal of China Coal Society,1997,22(1):18-21.

[3]刘林.淮南潘集地区地表沉降初步研究[J].中国矿业大学报,1999,28(2):165-167.LIU Lin.Study on surface subsidence in Panji mining area[J].Journal of China University of Mining &Technology,1999,28(2):165-167.

[4]余学义,李邦帮,李瑞斌,等.西部巨厚湿陷性黄土层开采损害程度分析[J].中国矿业大学报,2008,37(1):43-45.YU Xue-yi,LI Bang-bang,LI Rui-bin,et al.Analysis of mining damage in huge thick collapsible loess of western China mine[J].Journal of China University of Mining&Technology,2008,37(1):43-45.

[5]郑志刚,滕永海,王金庄,等.综采放顶煤条件下动态地表沉陷规律研究[J].矿山测量,2009,(2):61-62.ZHENG Zhi-gang,TENG Yong-hai,WANG Jin-zhuang,et al.Dynamic surface subsidence laws under conditions of fully mechanized coal caving[J].Mine Surveying,2009,(2):61-62.

[6]滕永海,王金庄.综采放顶煤地表沉陷规律及机理[J].煤炭学报,2008,33(3):264-267.TENG Yong-hai,WANG Jin-zhuang.The law and mechanism of ground subsidence induced by coal mining using fully-mechanized caving method[J].Journal of China Coal Society,2008,33(3):264-267.

[7]谭志祥,王宗胜,李运江,等.高强度综放开采地表沉陷规律实测研究[J].采矿与安全工程学报,2008,25(1):59-62.TAN Zhi-xiang,WANG Zong-sheng,LI Yun-jiang,et al.Field research on ground subsidence rules of intensive fully mechanized mining by sublevel caving[J].Journal of Mining &Safety Engineering,2008,25(1):59-62.

[8]黄平路,陈从新,肖国峰,等.复杂地质条件下矿山地下开采地表变形规律的研究[J].岩土力学,2009,30(10):3020-3024.HUANG Ping-lu,CHEN Cong-xin,XIAO Guo-feng,et al.Study of rock movement caused by underground mining in mines with complicated geological conditions[J].Rock and Soil Mechanics,2009,30(10):3020-3024.

[9]刘玉成,曹树刚.基于关键层理论的地表下沉盆地模型初探[J].岩土力学,2012,33(3):719-724.LIU Yu-cheng,CAO Shu-gang.Preliminary study of surface subsidence model based on theory of key rock stratum[J].Rock and Soil Mechanics,2012,33(3):719-724.

[10]国家煤炭工业局制定.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社,2010.

[11]李瞾,王金安.金沙河下采煤地表移动变形与导水裂隙带高度预测分析[J].中国矿业,2012,21(8):121-124.LI Zhao,WANG Jin-an.Predictive analysis of ground deformation and water flowing fracture height mining under Jinsha River [J].China Mining Magazine,2012,21(8):121-124.

[12]王金安,焦申华,唐君,等.开采扰动河床防渗治理方法[J].煤炭学报,2013,9,38(9):1549-1556.WANG Jin-an,JIAO Shen-hua,TANG Jun,et al.Anti-seepage control method for mining disturbed riverbed[J].Journal of China Coal Society,2013,9,38(9):1549-1556.

[13]李德仁,郑肇葆.解析摄影测量学[M].武汉:武汉大学出版社,2002.

[14]黄乐亭,王金庄.地表动态沉陷变形规律与计算方法研究[J].中国矿业大学报,2008,37(2):211-215.HUANG Le-ting,WANG Jin-zhuang.Research on laws and computational methods of dynamic surface subsidence deformation[J].Journal of China University of Mining &Technology,2008,37(2):211-215.

[15]KNOTHE S.Time influence on a formation of a subsidence surface[J].Archiwum Gómictwa i Hutnictwa,Kraków(in Polish),1952,1(1):1.

[16]彭小沾,崔希民,臧永强,等.时间函数与地表动态移动变形规律[J].北京科技大学学报,2004,8,26(4):341-344.PENG Xiao-zhan,CUI Xi-min,ZANG Yong-qiang,et al.Time function and prediction of progressive surface movement and deformation[J].Journal of University of Science and Technology Beijing,2004,8,26(4):341-344.

[17]崔希民,缪协兴,赵英利,等.论地表移动过程的时间函数[J].煤炭学报,1999,10,24(5):453-456.CUI Xi-min,MIAO Xie-xing,ZHAO Ying-li,et al.Discussion on the time function of time dependent surface movement[J].Journal of China Coal Society,1999,10,24(5):453-456.

[18]刘玉成,庄艳华.地下采矿引起的地表下沉的动态过程模型[J].岩土力学,2009,30(11):3406-3416.LIU Yu-cheng,ZHUANG Yan-hua.Model for dynamic process of ground surface subsidence due to underground mining[J].Rock and Soil Mechanics,2009,30(11):3406-3416.

[19]刘玉成,曹树刚,刘延保.改进的Konthe 地表沉陷时间函数模型[J].测绘科学,2009,9,34(5):16-17.LIU Yu-cheng,CAO Shu-gang,LIU Yan-bao.The improved Knothe time function for surface subsidence[J].Science of Surveying and Mapping,2009,9,34(5):16-17.

[20]何国清.矿上开采沉陷学[M].北京:中国矿业大学出版社,1994.