轻质量及中质量核结构的壳模型研究
袁岑溪 亓 冲
1(中山大学 中法核工程与技术学院 珠海 519082)
2(瑞典皇家工学院 瑞典 斯德哥尔摩 SE-10691)
轻质量及中质量核结构的壳模型研究
袁岑溪1亓 冲2
1(中山大学 中法核工程与技术学院 珠海 519082)
2(瑞典皇家工学院 瑞典 斯德哥尔摩 SE-10691)
壳模型被广泛应用于研究轻质量及中质量核的性质,它能很好地描述这些原子核的基态和低激发态的能量、电磁矩和电磁跃迁以及β衰变等性质。本文简要介绍了原子核壳模型的基本框架,如何选择单粒子基矢和构建模型空间和有效哈密顿量。对不同区域的原子核的壳模型最新研究做了回顾。在psd区,介绍一个新的相互作用成功地描述碳、氮、氧的中子滴线及其它性质以及A=20附近弱束缚丰质子核的谱学性质;在fp区,介绍了N=Z奇奇核中不同同位旋形成的转动带,以及通过N=Z附近的镜像核研究核力的电荷对称性破缺;在更重的区域,介绍了92Pd这个N=Z的原子核中同位旋标量质子中子对起主导作用,以及Sn同位素的研究。
原子核壳模型,轻质量及中质量核,低激发态,能谱,电磁跃迁,质子中子对
我国和其它国家近年来投入巨资兴建或升级大型放射性束装置,新一代放射性束装置极大地增加了人们对原子核的认识,越来越多的非稳定原子核甚至滴线附近的原子核被发现和研究[1]。研究这些远离稳定线的原子核的基态能量、能谱、衰变等性质,有助于我们更全面地认识和利用原子核。原子核是一个量子多体体系,如何求解这个多体问题是个难题,常用的方法大概分为三类:从头计算(ab initio)方法、基于平均场近似的方法、原子核壳模型。原子核壳模型从薛定谔方程出发,在截断的模型空间计算,相比于ab initio方法大大减小了计算量,可以在单机及小型服务器上实现计算。壳模型计算中包含模型空间的组态混合,通过对角化过程同时给出基态和激发态,能够很好地描述原子核的结合能、能谱、电磁矩、跃迁和β衰变等性质,广泛应用于轻质量和中质量核区的研究[2-3]。本文总结了壳模型的基本框架,介绍了作者近年来对不同区域原子核的壳模型研究的进展。
1 原子核壳模型简介
原子核中质子中子数为2、8、20、28、50等数值时,原子核特别稳定,这些数被称为幻数。幻数的存在可以由核素丰度、原子核结合能和激发能等实验数据证实[4],这些证据表明原子核存在壳层结构。20世纪50年代,Mayer等[5]用自旋轨道耦合相互作用解释了原子核的幻数。通过中心力加自旋轨道耦合力,求解薛定谔方程得到单粒子轨道,原子核基态为质子和中子分别从低到高占据轨道,这就是简单壳模型或称为独立粒子模型。
独立粒子模型没有考虑核子间的“剩余”相互作用,现代壳模型即相互作用壳模型包含“剩余”两体相互作用,这时原子核为组态混合态。对于一个原子核,质子和中子在各个轨道上分布。原子核的态可以看作所有可能分布的叠加。原则上可以通过求解薛定谔方程得到原子核的能量和波函数,但对于绝大多数原子核,质子数中子数比较多,实际计算受到限制。基于壳结构,计算时可以选择一个核心,通常核心的质子中子都是幻数。不考虑核心的激发,考虑其他价核子的激发,在价空间求解薛定谔方程,从而得到原子核各个态的波函数和本征能量。
壳模型的基本框架包含:选择球形单粒子基矢、构建模型空间和有效哈密顿量。壳模型计算基于一组球形基,原则上可以用任意球形基。实际上在求解能量本征方程时,即从壳模型哈密顿量求解原子核的波函数这一过程,并不依赖于基的具体形式。但在构建壳模型哈密顿量和利用原子核波函数计算电磁矩和电磁跃迁等性质时,需要用到球形基的径向单粒子波函数的具体形式,通常选择谐振子基作为基矢。有了单粒子波函数构成的一组基矢,原子核单组态就可以写为这组基矢的Slater行列式,原子核波函数就是模型空间内所有可能的组态的叠加。
有了原子核波函数,就可以通过求解薛定谔方程得到原子核波函数和本征能量。但实际上描述大多数原子核所需要的谐振子基非常庞大,所以壳模型计算中构建模型空间至关重要。首先选取一个核心,通常取一个双幻核作为核心。核心以外取一些轨道作为模型空间,考虑到计算量,通常取一到两个大壳作为模型空间,这里一个大壳的意思是包含一个主量子数N对应的所有轨道。价空间中的核子可以在价空间中的各个轨道运动,这些轨道是开放的。价空间以外空间的所有轨道冻结,即不能有核子激发到这个轨道。对于研究的原子核,选择的模型空间要包括这些原子核的低激发态的重要组态。壳模型常用模型空间有:sd空间,取16O作为核心;fp空间,取40Ca为核心。包含两个大壳的空间有psd空间,取4He作为核心,如图1所示。

图1 psd模型空间示意图Fig.1 Schematic figure of psd model space.
确定了模型空间后,需要在此空间求解薛定谔方程:
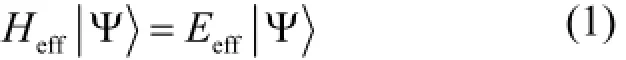
有效哈密顿量从核力出发,核子核子势模型大概可以分两类:一类是唯象的,用Yukawa等形式的函数拟合实验数据;一类是介子交换形式的,即单波色子交换势,从介子拉氏量出发,耦合常数通过拟合介子核子散射和核子核子散射数据得到。1990年以来人们根据大量更为精确的实验数据,提出了现代核子核子势,或称为高精度核子核子势,比如唯象的AV18势[6]和介子交换的CD-Bonn势[7]。可以通过这些核子核子势,也称为现实核力,做壳模型计算,称为现实壳模型。这需要重整化核力,即去除强排斥芯效应和考虑价空间外部空间的影响这两步重整化[8]。也可以用拟合核结构数据得到的有效哈密顿量做壳模型计算,称为唯象壳模型。唯象哈密顿量两体相互作用矩阵元可以通过拟合核结构数据,包括结合能、能级等实验数据得到,而哈密顿量单粒子能部分通常取接近实验值。
壳模型计算的维数非常庞大,是大规模数值计算。如何实现这样的计算是一个有着几十年历史并不断进步的前沿问题。最早的壳模型程序是通过jj耦合实现的,jj耦合维数小,但需要计算母分系数,对于多体问题这一系数的计算非常复杂。Glasgow组的Whitehead等[9]发展了在M-scheme展开的壳模型程序,并引入了Lanczos对角化算法这一壳模型对角化中的重要方法。在M-scheme展开做壳模型计算的程序中,应用最广泛的是Antoine程序。M-scheme计算方便,但维数大,jj-scheme计算维数小,但母分系数计算复杂。OXBASH程序吸收了这两个scheme计算方面的优点,即在M-scheme中生成基矢,投影到jj-scheme,这样避免了复杂的母分系数计算,又利用了jj-scheme维数小的优点。作者等[10]也编写了类似OXBASH算法的程序,优化了投影方法并实现了并行计算。
2 轻质量及中质量原子核的壳模型研究
2.1 psd区原子核
从稳定线到滴线,由于核力作用,壳结构可能发生变化,新的幻数可能产生,这些现象称为壳演化。近年来,很多工作研究了质子中子相互作用特别是其高阶项(张量力)对壳演化的影响。核力的其他成分也同样地可能对壳演化有所贡献。从氧同位素到氮同位素再到碳同位素,N=14同中素的激发能下降很快,表明N=14壳在氧同位素中存在,在氮同位素中减弱,在碳同位素中基本消失。我们对这一壳演化过程进行了更细致的讨论,把核力中各个部分相互作用对壳演化的贡献计算出来。结果表明中子中子相互作用在中子数N=14壳演化过程中起到重要作用[11]。
psd区域中,人们已经提出了一些有效相互作用,比如1975年提出的MK相互作用,1992年提出的WBT和WBP相互作用。MK、WBT和WBP是在(0-1)ħω模型空间中构建的,(0-1) ħω态和(2-3) ħω态之间的混合没有被考虑,对一些远离稳定线原子核的性质描述不好,比如不能正确给出碳氧同位素的滴线。我们提出了一个新的psd区的有效相互作用[12]。此相互作用可以同时正确给出碳、氮、氧同位素的滴线位置,比如给出的22C的双中子分离能为106keV,根据之后发表的首次观测值[13]计算可得双中子分离能实验值为110keV。此相互作用同样可以很好地描述硼、碳、氮、氧等同位素的激发能级、电四极矩、磁矩和β衰变等。
研究丰质子核对理解天体物理非常重要,比如17F(p,γ)18Ne反应在恒星爆炸过程起了重要作用,丰质子核的结合能和能谱是计算这些反应所必需的。通常这些能谱和丰质子核镜像核的能谱非常接近,因为强相互作用几乎电荷无关,库仑相互作用对能级的影响很小,镜像核能级差(Mirror Energy Difference, MED)通常为0.1MeV左右。一些特殊的镜像态之间,MED可以远大于0.1MeV,比如18Ne的3+态比18O的低了0.82MeV。这是由于价质子占据弱束缚1s1/2轨道时,库仑力的排斥相对较弱。因为1s1/2轨道没有离心位垒,波函数的径向部分比别的轨道更向外延伸。在一个包含多个价核子的体系中,丰质子核中价质子之间的剩余相互作用比相应镜像核中丰中子之间的剩余相互作用要弱,因为价质子更弱束缚波函数向外延伸。可以看出如果想从镜像核研究丰质子核,既要修正单粒子能级,也要减弱剩余相互作用。我们考虑弱束缚丰质子核中的价核子弱束缚效应,修正了sd区常用的USD系列相互作用,研究了质量数A=20附近丰质子核的性质[14]。通过修正后的相互作用可以很好地描述丰质子原子核的结合能、能级和MED。
2.2 fp区原子核
在N=Z的核中,质子中子对的T=0和T=1成分以及它们之间的竞争关系都有可能起很重要的作用。在很轻的N=Z的奇奇核中,基态一般占据同位旋最低T=0的态。但随着粒子数的增加,T=1的态的能量逐渐降低。从fp壳层开始,T=1的态成为N=Z的奇奇核的基态。对于46V和50Mn,人们发现T=0和1的组态都可以形成转动谱,系统性地研究这些核的谱学对我们理解原子核的配对性质有重要作用。基于CD-Bonn势,我们计算了fp壳层N=Z奇奇核的低激发态结构,很好地描述了这些核中T=0和1态之间的相对位置和衰变性质。作为例子,我们系统地计算了46V和50Mn的T=0和1的转动带性质并与已有的实验结果做了比较。计算表明,这些T=0和1的带内E2跃迁很强而且带间有很强的M1跃迁[15]。
前文提到,在轻核中,MED等镜像核的能量差别主要来自库仑能。而0f7/2壳核的一个特别性质就是库仑能对激发态的能量和衰变性质影响较小,主要是因为这些态的波函数主要组分都是0f7/2。这为我们研究核子力的同位旋不对称或电荷对称性破缺效应提供了特别的条件。我们基于CD-Bonn核子核子相互作用计算了fp壳层T=1/2镜像核的结构和衰变性质。计算的能级结构与实验以及基于唯象相互作用的计算都能很好地符合[16]。0f7/2核中的镜像能量差电荷对称性破缺效应的贡献可能和库仑力具有同等的重要性。基于电荷相关的高精度CD-Bonn势,我们计算了这些镜像核的镜像能量差以及电荷对称性破缺效应的矩阵元强度,并与唯象抽取的强度做了比较。
2.3 g9/2轨道及更重的原子核
对于单j轨道上的3或4核子态,可以通过角动量分解的方法给出能量的解析解,有些重要的态的解析形式非常简单,有助于研究辛弱数守恒与否的性质[17]。g9/2轨道上4核子态有两个特别的组态,自旋为4和6且辛弱数都为4。这两个态是任意两体相互作用的本征态,即这两个态的辛弱数在任意相互作用下是好量子数,这个辛弱数部分守恒的例子可以被解析地证明,而对于j≤15/2的轨道上的其他核子数和自旋数的情况则不成立[18]。在辛弱模型基础上,我们也研究了同位旋矢量质子中子关联对原子核结合能的影响[19]。
最近对92Pd的低激发态能谱的测量表明:在这个非常重的N=Z的核的基态和激发态中,自旋顺排的同位旋标量质子中子对可能会取代通常的超流态成为主导,这个很强的同位旋标量关联对进一步研究核结构和快质子俘获过程很有意义[20]。进一步的壳模型研究表明,这些同位旋标量质子中子对更倾向于耦合成g9/2轨道上允许的最大的角动量J=9,这一特性和其他的所有偶偶核都不一样[21]。这样的质子中子对形成的低激发能谱有如下特征:(1) 能级近乎等间隔;(2) I到I-2的态跃迁概率近似为常数且具有强选择性。这一独特的激发模式在接近双幻核100Sn的N=Z原子核中取代了同位旋矢量耦合。
基于CD-Bonn势,我们研究了102-132Sn等原子核的性质[22],哈密顿量中的单粒子能和单级相互作用通过对这些核低激发转晕态的结合能拟合而得。基于此哈密顿量,我们研究了101Sn和103Sn的自旋反转及可能的超出普通对关联的相互作用的贡献。
3 结语
本文回顾了壳模型的基本框架和一些最新进展。在轻核区,原子核的研究已达到中子滴线,一个新的psd区相互作用能够同时正确给出碳、氮、氧的滴线位置。A=20质子滴线附近的弱束缚核需要同时考虑单粒子能和两体相互作用的修正。N=Z附近的核对研究质子中子对关联性质有重要帮助,在fp区46V和50Mn的T=0和T=1的态都可以形成转动带,在g9/2轨道92Pd被发现自旋顺排的同位旋标量质子中子对组态占据主导。壳模型非常适合研究此类质子中子对关联性质。fp区的镜像核库仑能差对能级的差别影响较小,可以用来研究核力的电荷对称性破缺。从轻质量到中质量核,壳模型对理解原子核结构发挥着重要的作用。
致谢感谢许甫荣教授、Otsuka教授、Suzuki教授等的讨论和建议。
1 Thoennessen M. Reaching the limits of nuclear stability[J]. Reports on Progress in Physics, 2004, 67: 1187-1232
2 Brown B A. The nuclear shell model towards the drip lines[J]. Progress in Particle and Nuclear Physics, 2001, 47: 517-599
3 Caurier E, Martinez-Pinedo G, Nowacki F, et al. The shell model as a unified view of nuclear structure[J]. Reviews of Modern Physics, 2005, 77: 427-488
4 卢希庭, 江栋兴, 叶沿林. 原子核物理(修订版)[M]. 北京: 原子能出版社, 2000
LU Xiting, JIANG Dongxing, YE Yanlin. Nuclear physics (revised edition)[M]. Beijing: Atomic Energy Press, 2000
5 Mayer M G, Jensen J H D. Elementary theory of nuclear shell structure[M]. New York: Wiley, 1955
6 Wiringa R B, Stoks V G J, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking[J]. Physical Review C, 1995, 51: 38-51
7 Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential[J]. Physical Review C, 2001, 63: 024001
8 Dean D J, Engeland T, Hjorth-Jensen M, et al. Effective interactions and the nuclear shell-model[J]. Progress in Particle and Nuclear Physics, 2004, 53: 419-500
9 Whitehead R R, Watt A, Cole B J, et al. Computational methods for shell-model calculations[J]. Advances in Nuclear Physics, 1977, 9: 123-176
10 Qi C, Xu F R. Shell-model studies of isomeric states in51,52,53Fe[J]. Chinese Physics C, 2008, 32(s2): 112-115
11 Yuan C X, Qi C, Xu F R. Shell evolution in neutron-rich carbon isotopes: unexpected enhanced role of neutron-neutron correlation[J]. Nuclear Physics A, 2012, 883: 25-34
12 Yuan C X, Suzuki T, Otsuka T, et al. Study of B, C, N, and O isotopes based on VMU[J]. Physical Review C, 2012, 85: 064324
13 Gaudefroy L, Mittig W, Orr N A, et al. Direct mass measurements of19B,22C,29F,31Ne,34Na and other light exotic nuclei[J]. Physical Review Letters, 2012, 109: 202503
14 Yuan C X, Qi C, Xu F R, et al. Mirror energy difference and the structure of loosely bound proton-rich nuclei around A=20[J]. Physical Review C, 2014, 89: 044327
15 Qi C, Xu F R. Shell-model study of spectroscopies and isospin structures in odd-odd N=Z nuclei employing realistic NN interaction[J]. Nuclear Physics A, 2008, 800: 47-62
16 Qi C, Xu F R. Isospin asymmetry effects in mirror nuclei with modern charge-dependent NN potential[J]. Nuclear Physics A, 2008, 814: 48-65
17 Qi C. Energy expressions for n=3 and 4 systems in a single-j shell[J]. Physical Review C, 2010, 81: 034318
18 Qi C. Partial conservation of seniority in the j=9/2 shell: analytic and numerical studies[J]. Physical Review C, 2011, 83: 014307
19 Qi C. Double binding energy differences: mean-field or pairing effect?[J]. Physics Letters B, 2012, 717: 436-440 20 Cederwall B, Moradi F G, Bäck T, et al. Evidence for a spin-aligned neutron-proton paired phase from the level structure of92Pd[J]. Nature, 2010, 469: 68-71
21 Qi C, Blomqvist J, Bäck T, et al. Spin-aligned neutron-proton pair mode in atomic nuclei[J]. Physical Review C, 2011, 84: 021301(R)
22 Qi C, Xu Z X. Monopole-optimized effective interaction for tin isotopes[J]. Physical Review C, 2012, 86: 044323
CLCTL11
Recent shell-model studies of light and medium-mass nuclei
YUAN Cenxi1QI Chong2
1(Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-Sen University, Zhuhai 519082, China) 2(Royal Institute of Technology, AlbaNova University Center, Stockholm SE-10691, Sweden)
Background: Nuclear shell model is widely applied in the studies of light and medium-mass nuclei. The ground and excited state energies, electromagnetic properties and β decay properties of these nuclei can be well understood by solving many body Schrödinger equation with effective shell-model Hamiltonian in the model space. Purpose: The aim is to introduce the framework of shell model and its application in nuclei. Methods: The nuclear shell model is used to study properties of selected nuclei. Results: In psd region, a new effective shell-model Hamiltonian is introduced. The neutron drip-line of C, N, and O isotopes can be given with such Hamiltonian. The nuclei around A=20 with weakly bound proton are investigated through a modified shell model Hamiltonian. N=Z nucleus is good for studying the effect of proton-neutron pair.46V and50Mn have both T=0 and 1 rotational band.92Pd can be understood under a spin alignment isoscalar scheme of proton-neutron pair. Mirror nuclei around N=Z in fp region can be used for the investigation of charge symmetry breaking effect of nuclear force. Conclusion: Nuclear shell model is proper and useful for the description of light and medium-mass nuclei.
Nuclear shell model, Light and medium-mass nuclei, Low-lying states, Energy level, Electromagnetic transition, Proton-neutron pair
TL11
10.11889/j.0253-3219.2014.hjs.37.100503
国家自然科学基金(No.11305272)、高等学校博士学科点专项科研基金(No.20130171120014)资助
袁岑溪,男,1984年出生,2012年于北京大学获博士学位,原子核结构专业
2014-04-25,
2014-09-20

