一种新方式描述具有X(5)对称性的原子核
戴连荣 丛美玲 刘入菱 邓 鑫 刘 琦
(辽宁师范大学 物理系 大连 116029)
一种新方式描述具有X(5)对称性的原子核
戴连荣 丛美玲 刘入菱 邓 鑫 刘 琦
(辽宁师范大学 物理系 大连 116029)
相互作用玻色子模型(Interacting boson model, IBM)是一个代数模型,它能很好地描述原子核的集体运动性质。由于IBM中玻色子数守恒及有可解析解,因而能方便地研究原子核过渡区的行为。本文在IBM模型中引入了一种新的方案,即用O(6)高阶项替代传统方案的SU(3)四极-四极相互作用来描述轴对称转动核。在此基础上,对过渡区具有X(5)对称性的原子核的量子相变现象进行了系统的研究。分别在两种方案下,研究了原子核154Gd和98Sr低激发态的能谱和电磁跃迁性质。结果表明,采用新的O(6)高阶项相互作用可以更好地描述实验结果,特别是描述不同带之间的带间跃迁性质。
相互作用玻色子模型,量子相变,高阶项
原子核形状相变及临界点对称性的研究是物质深层次结构的前沿领域和热点问题,探索与原子核结构和形状相变相关的新对称性十分重要。量子形状相变的特性在理解有限多体系统的动力学行为时极其重要[1-3]。许多原子核系统的特性都与形状相关,特别让人感兴趣的是不同形状之间过渡区及临界点的性质。
原子核的相互作用玻色子模型(Interacting boson model, IBM)是一个代数模型,它用来描述原子核的集体运动。IBM中存在三种动力学对称性极限,其分别对应三种集体运动模式并对应着原子核的三种几何形状即球形核的U(5)振动极限、椭球形核的SU(3)转动极限和不稳定核的O(6)极限[4-6]。只考虑这三种极限的相图称为Casten三角形,从一种极限过渡到另一种极限对应着从一种几何形状到另一种几何形状,在这三种极限之间的区域称为过渡区。由于IBM中玻色子数守恒及有可解析解,因而能方便有效地研究原子核过渡区的量子相变行为。研究发现,大部分原子核处在这三种极限的过渡区域,因此对于量子相变和临界点对称性的研究成为关注的焦点。本文研究原子核从球形振动到轴对称转动过渡区具有X(5)对称性核的结构和性质。
我们曾在最近的工作中[7-8],对上面提到的两种方案进行了系统的研究,研究了不同玻色子数下系统从振动到转动过渡区的原子核量子相变特征,计算了一些感兴趣物理量如低激发态能级比和电四极跃迁比、玻尔形变参量的基态期待值及均方根偏差值等,对具有X(5)对称性核如152Sm和150Nd,计算了低激发态能谱和电四极跃迁性质,并和实验数据进行了对比分析,发现O(6)高阶项相互作用可以用来描述X(5)对称性核的特性,特别是可以更好地描述不同带之间的带间跃迁性质。这一研究具有理论意义,它揭示了一种新的代数结构来描述原子核的结构。在此基础上研究其他的X(5)对称性核候选者,进一步检验O(6)高阶项这一代数结构是否可以描述更多的原子核是有意义的。
1 哈密顿量
IBM模型的哈密顿量可由Casten三角形上整个区域的控制参量的变化来描述,两个极限之间的临界点会发生量子相变[9-11]。原子核从球形向轴对称形变化的U(5)-SU(3)过渡区的临界点具有X(5)对称性[12-13]。
文献[14]中曾利用SU(3)四极-四极相互作用方案对这一区域的量子相变行为的相关物理量做过系统的研究,这一方案称为U(5)-SU(3)方案,其哈密顿量为:
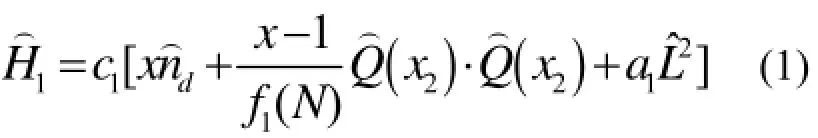
最近Isacker[15]提出了不仅可以用SU(3)四极-四极相互作用来描述转动谱,也可以用O(6)高阶项来描述原子核的转动谱,Thiamova等[16]进一步验证了这一结论。因而本文将利用O(6)高阶项代替传统的SU(3)四极-四极相互作用来描述原子核从球形向轴对称形变化过渡区具有X(5)对称性核,这一方案称为UQ方案,其哈密顿量为:

2 计算结果与讨论
对原子核的转动谱可以采用SU(3)四极-四极相互作用描述,也可以用O(6)高阶项来描述。原子核从振动到转动过渡区的原子核量子相变行为可以用上面提到的两种方案进行,并且我们曾对中子数为90的具有X(5)对称性核152Sm和150Nd进行了有意义的研究。继续对其他的X(5)核候选者进行研究是让人感兴趣的,本文利用上面提到的两种方案,研究另外一个中子数为90的X(5)核候选者154Gd核和一个中子数为60的98Sr核,研究这两个核的低激发态能谱和电四极跃迁性质。
2.1154Gd核的结构
表1给出了U(5)-SU(3)方案和UQ方案下154Gd核能谱的计算结果并与实验值[17]进行了对比分析。表1中下标1代表基带,下标2和3分别代表β带和γ带。σ(E)表示能量的实验值偏离理论值的均方偏差大小[7]。结果表明,UQ方案也可以用来描述154Gd核的低激发态能级;对γ带,UQ方案比U(5)-SU(3)方案更接近实验值。
表2给出了U(5)-SU(3)方案和UQ方案下电四极跃迁性质的计算结果并与实验值[17]进行了比较。σ(BE2)表示电四极跃迁的实验值偏离理论值的均方偏差大小[7]。结果表明UQ方案也可以用来描述154Gd核的电四极跃迁性质,且比U(5)-SU(3)方案更接近实验值。

表1 154Gd能级的实验和理论值(keV)Table1 Calculated results and experimental data of 154Gd energy levels (keV).

表2 154Gd核的电四极跃迁值(W.u.)Table2 Calculated results and experimental data of 154Gd E2 transitions (W.u.).
2.298Sr核的结构
另一个感兴趣的X(5)核候选者之一是中子数为60的98Sr核,我们对其低激发态的能级和电四极跃迁性质也进行了初步的研究。表3给出了两种方案下98Sr核能谱的计算结果并与有准确信息的实验值[18]进行了比较。结果表明,UQ方案也可以用来描述98Sr核的低激发态能级,并且比U(5)-SU(3)方案更接近实验值。特别是β带的带头20+态的能量,实验值为215.4 keV,U(5)-SU(3)方案和UQ方案下的理论结果分别为307.4 keV和211.1 keV,可以看到UQ方案极大地改进了β带的带头能量。
表4给出了两种方案下98Sr核电四极跃迁性质的计算结果并与实验数据[18]进行了比较。结果表明,UQ方案也可以用来描述98Sr核的电四极跃迁性质;对于β带到基带的带间跃迁,实验值为57.0 W.u.,U(5)-SU(3)方案和UQ方案下的理论结果分别为58.9 W.u.和56.0 W.u.,表明UQ方案可以改进这一带间跃迁性质并使之更接近实验值。
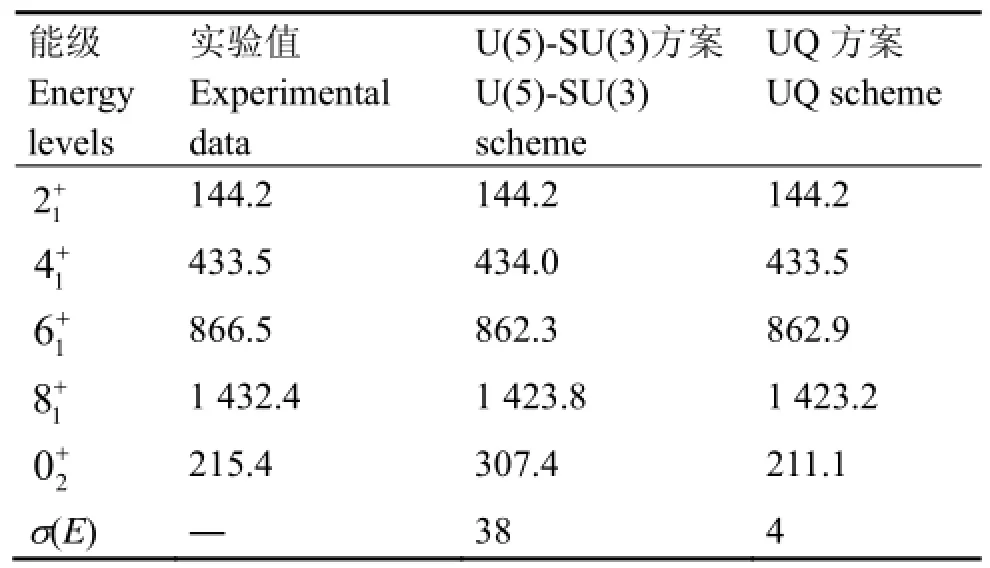
表3 98Sr能级的实验和理论值(keV)Table3 Calculated results and experimental data of 98Sr energy levels (keV).
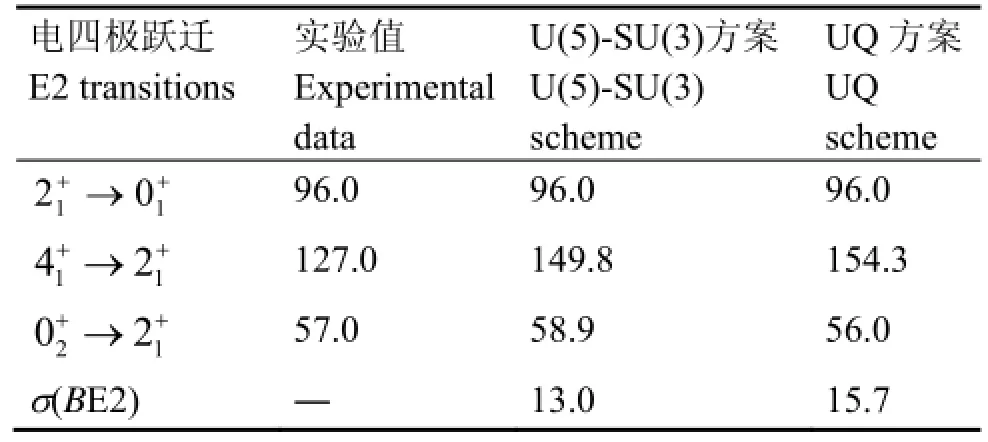
表4 98Sr核的电四极跃迁值(W.u.)Table4 Calculated results and experimental data of 98Sr E2 transitions (W.u.).
2.3结果的定性分析
以上用两种方案定性分析了两个可能的X(5)核候选者,其中一个是中子数为90的154Gd核,另一个是中子数为60的98Sr核。初步计算结果表明,U(5)-SU(3)方案和UQ方案均可以用来描述原子核从球形振动到轴对称转动过渡区具有X(5)对称性核的结构和性质。通过对原子核不同能级的拟合分析,发现哈密顿量中的2ˆL项会直接影响20+态的能量。这一点可以清楚地从表3中的98Sr核中看到,UQ方案极大地改进了β带的带头能量,从而表明O(6)高阶项这一新的代数结构或许比SU(3)四极-四极相互作用更合适用来描述轴对称转动核以及与之相应的描述X(5)核的结构和性质。
3 结语
本文利用O(6)高阶项代替传统的SU(3)四极-四极相互作用来研究原子核从振动到转动过渡区具有X(5)对称性原子核的结构和性质。在两种方案下,分别研究了具有不同中子数的154Gd核和98Sr核的低激发态能谱和电四极跃迁性质。结果表明,可以用O(6)高阶项代替SU(3)四极-四极相互作用来描述这两个原子核的性质。O(6)高阶项这一新方案,可以用来描述从振动到转动过渡区具有X(5)对称性的原子核的量子相变特征。O(6)高阶项相互作用提供了一种新的代数结构,也许可以用来描述更感兴趣的其他实验结果,值得未来进行更深入的研究。
1 Rowe D J, Thiamova G. The many relationships between the IBM and the Bohr model[J]. Nuclear Physics A, 2005, 760(1): 59-81
2 Thiamova G. The IBM description of triaxial nuclei[J]. The European Physical Journal A, 2010, 45(1): 81-90
3 Fortunato L, Alonso C E, Arias J M, et al. Phase diagram for a cubic-Q interacting boson model hamiltonian: signs of triaxiality[J]. Physical Review C, 2011, 84: 014326
4 Arima A, Iachello F. Interacting boson model of collective states I the vibrational limit[J]. Annals of Physics, 1976, 99(2): 253-317
5 Arima A, Iachello F. Interacting boson model of collective nuclear states II the rotational limit[J]. Annals of Physics, 1978, 111(1): 201-238
6 Arima A, Iachello F. Interacting boson model of collective nuclear states IV the O(6) limit[J]. Annals of Physics, 1979, 123(2): 468-492
7 Dai L R, Pan F, Liu L, et al. Alternative characterization of the spherical to axially deformed shape-phase transition in the interacting boson model[J]. Physical Review C, 2012, 86: 034316
8 Dai L R, Zhong W W, Cong M L, et al. Description of150Nd nucleus by a new alternative scheme[J]. Chinese Physics C, 2013, 37(12): 124101
9 Dieperink A E L, Scholten O, Iachello F. Classical limit of the interacting-boson model[J]. Physical Review Letters, 1980, 44(26): 1747-1750
10 Dieperink A E L, Scholten O. On shapes and shape phase transitions in the interacting boson model[J]. Nuclear Physics A, 1980, 346: 125-138
11 Feng D H, Gilmore R, Deans S R. Phase transitions and the geometric properties of the interacting boson model[J]. Physical Review C, 1981, 23(3): 1254-1258
12 Scholten O, Iachello F, Arima A. Interacting boson model of collective nuclear states III the transition from SU(5) to SU(3)[J]. Annals of Physics, 1978, 115(2): 325-366
13 Iachello F. Analytic description of critical point nuclei in a spherical-axially deformed shape phase transition[J]. Physical Review Letters, 2001, 87(5): 052502
14 Pan F, Draayer J P, Luo Y A. Close look at U(5)-SU(3) transitional patterns in the interacting boson model[J]. Physics Letters B, 2003, 576: 297-302
15 Van Isacker P. Dynamical symmetry and higher-order interactions[J]. Physical Review Letters, 1999, 83: 4269-4272
16 Thiamova G, Cejinar P. Prolate-oblate shape-phase transition in the O(6) description of nuclear rotation[J]. Nuclear Physics A, 2006, 765: 97-111
17 Harmatz B. Nuclear data sheets for A=154[J]. Nuclear Data Sheets, 1979, 26(2): 281-384
18 Singh B. Nuclear data sheets for A=98[J]. Nuclear Data Sheets, 1998, 84(3): 565-716
CLCTL11
A new alternative scheme to describe nuclei with X(5) symmetry
DAI Lianrong CONG Meiling LIU Ruling DENG Xin LIU Qi
(Department of Physics, Liaoning Normal University, Dalian 116029, China)
Background: Quantum phase transition is of great interest in many areas of physics. Purpose: In this work, a new scheme is applied to describe the transitional nuclei with X(5) symmetry, from spherical to axially deformed shape-phase transition. Methods: In this new scheme, the usual SU(3) quadrupole-quadrupole interaction is replaced by an O(6) cubic interaction in the Interacting boson model (IBM). Results: The two X(5) candidates154Gd and98Sr nuclei are firstly investigated. The low-lying energy levels and E2 transition rates are calculated and compared with the experimental data. Conclusion: The results show that the new scheme can reasonably describe the experimental low-lying spectrum and the intraband and the interband E2 transitions. The present work is meaningful in understanding the new characteristics of symmetry by the higher order O(6) cubic interaction.
Interacting boson model (IBM), Quantum phase transitions, Higher-order term
TL11
10.11889/j.0253-3219.2014.hjs.37.100505
国家自然科学基金(No.11375080)和辽宁省科学技术基金(No.201320091)资助
戴连荣,女,1968年出生,1996年于中国科学院高能物理研究所获博士学位,现从事核结构和中高能核物理研究
2014-04-29,
2014-06-21

