不同长度的三维四向编织复合材料T型梁模态性能研究
王 欢,李嘉禄(., ;., )
振动是复合材料制件在应用中普遍存在的问题之一。随着复合材料制件尤其是三维编织复合材料制件在航空航天领域中的应用愈来愈广泛,其振动问题也越来越受到关注。因此,为避免在使用中造成不必要的损失,对三维编织复合材料制件的振动研究也就显得尤为重要。
目前国内外都有关于复合材料制件振动性能的研究。刘兵山等[1]进行了复合材料机翼盒段结构的模态分析和试验,两者结果吻合较好。王军等[2]在没有对复杂结构进行简化的前提下,利用ANSYS有限元软件建立了完整的某直升机复合材料旋翼桨叶,并计算了桨叶在额定转速下的前5阶固有模态和频率。李建华等[3]在abaqus环境下,建立复合材料叶片,划分网格,施加约束,并采用有限元方法进行模态分析,同时讨论了复合材料叶片动力刚化效应对振动的影响,为叶片结构设计提供了有价值理论的参考。T.H.Ooijevaar等[4]将振动试验与模态应变能损伤算法相结合,通过利用模态实验中获得的频率发现了损伤的存在,并由试验获得的阵型准确地做出了损伤定位。Jaehong Lee等[5]研究了工字形截面复合材料薄壁梁的振动,它基于经典的层和理论,研究了不同铺层顺序、对称与非对称铺层、边界条件对弯曲和扭转模态的影响。并用1维的有限元模型预测了梁的固有频率和相应的阵型。本文对不同自由端长度的三维编织复合材料T型梁制件的模态性能进行了研究。采用单输入/单输出的频域模态参数识别方法,确定了自由端长度对复合材料T型梁固有频率的影响及固有频率与阻尼性能的关系。并把实验得到的固有频率和有限元模拟的结果进行了对比。
1 实验
1.1 T型梁试件
实验使用的三维四向编织复合材料T型梁试件是采用四步法编织工艺,再经RTM工艺复合固化制得。其中编织纱为 T700-12K碳纤维,密度为1.76 g/cm3,线密度为0.8 g/m;基体材料为TDE-86 型环氧树脂。本实验中采用的T型梁的纤维体积含量为51%,表面编织角为29°。图1为试件的实物图,其中腹板的尺寸为280 mm×20 mm×4.2 mm,肋板的尺寸为280 mm×21.2 mm×4.4 mm。在实验中通过改变T型梁试件加持区域的长度来改变其自由端的长度,实验中悬臂梁的自由端长度分别为255 mm、245 mm、235 mm、225 mm、215 mm。

图1 三维四向编织复合材料T型梁试件实物图
1.2 实验装置
图2为三维四向编织复合材料T型悬臂梁的振动模态实验系统的模拟图。用力锤在点A(位于远离肋板一侧的腹板平面的沿纤维方向的中心线上,距加持点约10 mm)沿与纤维垂直的方向激振,力锤上的力传感器感受力信号,同时用加速度传感器在另一点B(与点A在同一条直线上,接近T型梁顶端)测量加速度响应,这两个信号经 WS-2401滤波放大器放大后输入到WS-5921网络数据采集仪中,再由Vib'SYS模态分析软件进行分析计算,得到 B 点对A点的频率响应函数。最后由模态分析系统求得模态频率和阻尼比。

图2 模态测试装置连接图
2 实验结果与讨论
在实验中分别对不同自由端长度的三维四向编织碳纤维/环氧树脂复合材料T型梁进行了悬臂梁振动实验模态分析(每种长度有3个试件),获得了各个模态参数的平均值(阻尼比、固有频率) ,如表 1所示。

表1 试验获得的固有频率和阻尼比
2.1 长度对三维四向编织复合材料T型梁固有频率的影响
图3是不同自由端长度的三维四向编织复合材料T型梁试件的前两阶固有频率。从图3中可以看出前两阶固有频率都随着自由端长度的增加而减小。根据梁的振动理论,悬臂梁的一阶振动频率服从以下关系[6]:
(1)
式中,K1为对应一阶频率的系数(取1.875);l为梁自由端的长度,单位mm;E为梁的弹性模量,单位 GPa;h为平行于梁振动方向的高度,单位mm;ρ为梁的质量密度,单位g/mm3。由公式(1)可见,当梁的其它参数相同时,梁的一阶振动固有频率反比于梁自由端长度的平方。图4是一阶固有频率f和1/l2之间的关系图,并在图中做了拟合直线。当拟合优度R2的值越接近于1时,说明直线的拟合程度越好,图4中直线的拟合优度R2为99.94%,说明该直线的拟合程度很好。因此可以看出本实验中三维四向编织复合材料T型梁的固有频率确实随着自由端长度的增大而减小,且与1/l2呈线性关系,故实验结果是合理的。

图3 不同自由端长度的T型梁的固有频率
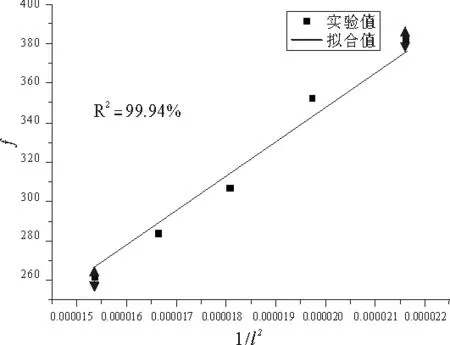
图4 T型梁的固有频率和1/l2的关系
2.2 长度和固有频率对阻尼的影响
图5中a图和b图分别展示了第一阶和第二阶的阻尼比与固有频率的关系,其中横坐标是固有频率,纵坐标是阻尼。从图5中可以明显地看出,对三维四向编织复合材料T型梁来说,它的固有频率和阻尼没有明显的相关关系,这个结论也和Shafi Ullah Khan[7]得出的结论相类似。由于固有频率与自由端长度之间的关系是单调的,所以长度和阻尼也没有明显的相关关系。
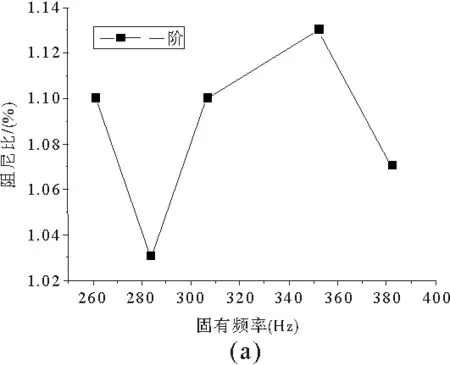
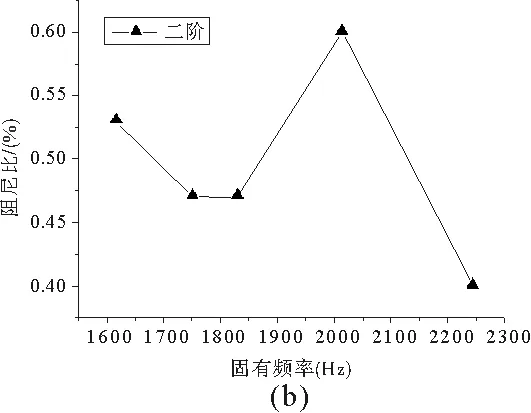
图5 T型梁阻尼比与其固有频率的关系
3 有限元模拟
运用ANSYS14.0软件建立了T型梁的实体有限元模型,模拟了T型梁的固有频率。采用六面体划分网格,对T型梁的端部固定约束,然后计算。计算中采用的弹性性能数据来自于李典森等[8]的三维四向编织复合材料弹性性能的有限元预报中,选取的是表面编织角为30.7°,纤维体积含量为55%的一组数据,这和本实验中所采用的数据相对比较接近。计算的固有频率结果与实验的固有频率结果对比如图6所示。


图6 固有频率对比
图6中a图和b图分别是第一阶和第二阶固有频率的对比,从图6中可以看出T型梁固有频率的模拟值和试验值还是比较一致的,尤其是第二阶固有频率。在所有的数据中,最小的百分比差值为0.7%,最大的百分比差值为6.8%,即实验结果和模拟结果的一致性较好。
4 结论
4.1当除自由端长度以外的其它参数相同时,三维四向编织结构的碳纤维/环氧树脂复合材料T型梁的固有频率随着其自由端长度的增加而减小。
4.2三维四向编织结构的碳纤维/环氧树脂复合材料T型梁的固有频率和其阻尼性能没有明显的相关关系。
4.3对于三维四向编织结构的碳纤维/环氧树脂复合材料T型梁,有限元模拟的固有频率与实验得到的固有频率相一致。
[1] 刘兵山,燕瑛,钱卫,等.复合材料机翼盒段的设计、模态分析和试验[J].北京航空航天大学学报,2003,29(11):1026—1028.
[2] 王军,冯国旭,杨亚东,等.直升机复合材料桨叶振动失效分析[J].失效分析与预防,2011,6(2):80—84.
[3] 李建华,毛文贵,傅彩明.复合材料风机叶片有限元模态分析[J].湖南工程学院学报(自然科学版),2011,21(1):28—30.
[4] T.H.Ooijevaar, R.Loendersloot,L.L.Warnet.Vibration based structural health monitoring of a composite T-beam[J].Composite Structures,2010,92(9):2007—2015.
[5] Jaehong Lee,Seung-Eock Kim.Free vibration of thin-walled composite beams with I-shaped cross-sections[J].Composite Structures,2002,55(2):205—215.
[6] 郑丽娟,赵玉涛,金明江,等.纤维/树脂/铝合金叠层复合材料的显微组织与阻尼性能[J].中国有色金属学报,2003,13(3):667—670.
[7] Shafi Ullah Khan, Chi Yin Li, Naveed A.Siddiqui,et al.Vibration damping characteristics of carbon fiber-reinforced composites containing multi-walled carbon nanotubes[J].Composites Science and Technology,2011,71(12):1486—1494.
[8] 李典森,卢子兴,蔺晓明,等.三维四向编织复合材料弹性性能的有限元预报[J].北京航空航天大学学报,2006,32(7):828—832.

