比率依赖Holling-Ⅲ捕食-食饵系统的多个周期解
朱长青,田德生
(1湖北工业大学工程技术学院,湖北 武汉430068;2湖北工业大学理学院,湖北 武汉430068)
近年来,重合度理论广泛应用于研究生态方程的周期解问题[1],本文就是考虑如下的一类比率依赖Holling-Ⅲ的食饵-捕食者模型
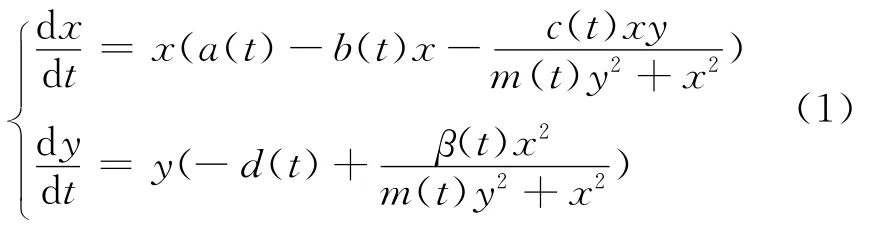
其中g为连续的ω-周期函数。
首先,引入重合度理论中的延拓定理[6]。
设X,Z是赋范向量空间,L:DomLX→Z为线性映射,N:X→Z为连续映射。称L为指标为零Fredholm算子,如果dim Ker L=codimImL< ’且ImL为Z中的闭集。如果L为指标为零Fredholm算子,又存在连续投影P:X→X和Q:Z→Z满足ImP
其中参数的生物意义参见文献[2]。环境变化对很多生物种群产生有着重要影响[3-4],特别是周期变化的环境带来的生物种群数量的周期波动,这促使我们考虑系统(1)中的参数都属于周期函数的情况。因此,假设a(t),b(t),c(t),d(t),β(t),m(t)是正的连续ω-周期函数,实际上这种假设与环境的周期变化(如气候的季节因素、食物的供给、生殖习惯等)相一致。本文研究系统(1)的周期解的存在性,与一般生态方程周期解的存在性研究[3-6]比较,在处理这些问题时用了新技巧,得到了新的结果。目前,运用重合度理论研究比率依赖Holling-Ⅲ的捕食-食饵系统周期解的存在性问题似乎尚不多见。
引理 设L是指标为零Fredholm算子,N在Ω是L-紧的,假设
(ⅰ)对任意的λ∈ (0,1),x∈Ω∩domL,都有Lx≠λNx;
(ⅱ)对任意的x∈Ω∩Ker L,都有QNx≠0;
(ⅲ)deg {JQN,Ω ∩ Ker L,0} ≠0。
则方程Lx=Nx在DomL∩Ω珚至少存在一个解。
应用重合度理论中的延拓定理讨论系统(1),得到如下结果。
证明 系统(1)过点 (x(0),y(0))的正轨线可写为
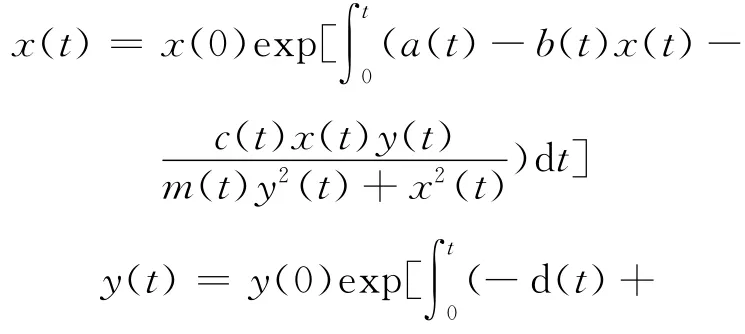
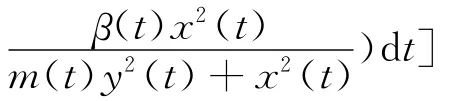
可见,当x(0)>0,y(0)>0,t≥0时,总有x(t)>0,y(t)>0。这表明从(x(0),y(0))出发的正轨线总停 留 在 第 一 象 限。 因 此,={(x,y)x≥0,y≥0} 是系统(1)的正不变集。令
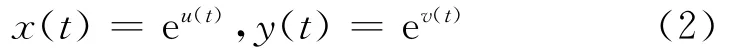
于是,系统(1)变为
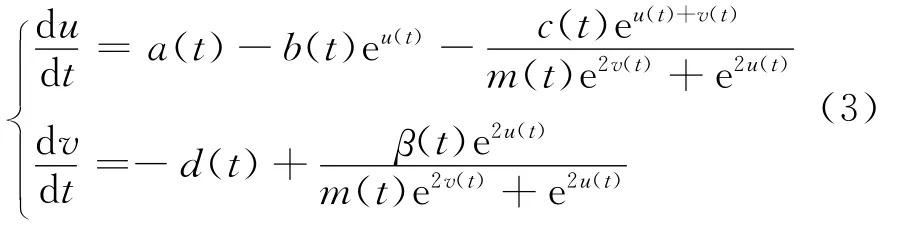
由变换(2)知,若 (u*(t),v*(t))为系统(3)的一个ω-周期解,则
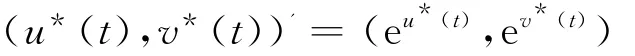
必为系统(1)的正ω-周期解。
故为证定理,只需证明系统(3)存在一个周期解即可,考虑辅助系统

其中λ∈ (0,1),假设(u(t),v(t))是系统(4)的一个ω-周期解。对式(4)两端从0到ω积分得
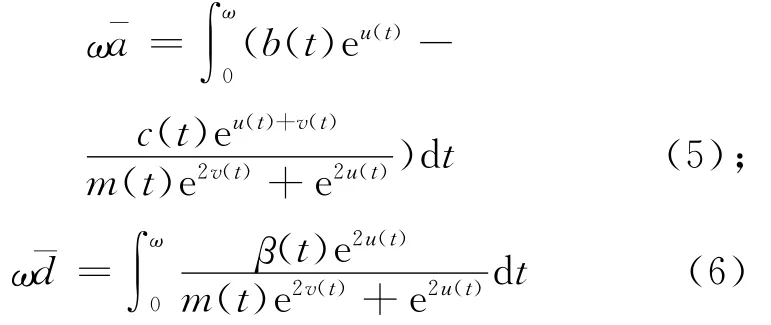
由式(4)—(6)得

选择ti,si∈ [0,ω],i=1,2,满足
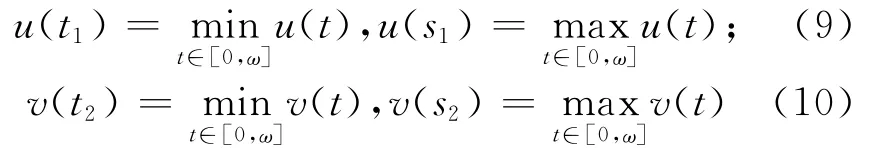
由(5)和(9)得
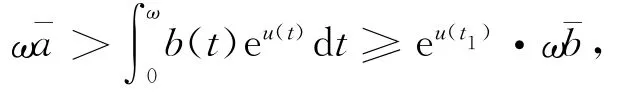
即

或者

由(7)和(11)得 t∈ [0,ω],有

由不等式a2+b2≥2ab和式(5)、式(9)得
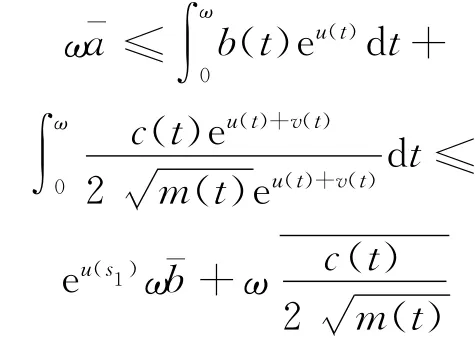
因此

或
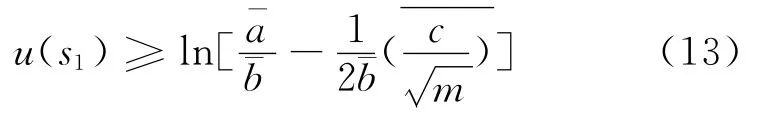
由(7)和(13)得,t∈ [0,ω],有


即
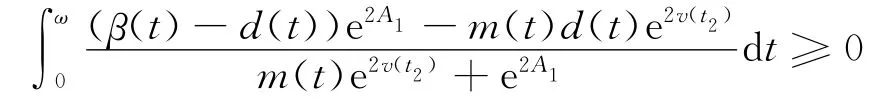
由第二积分中值定理得
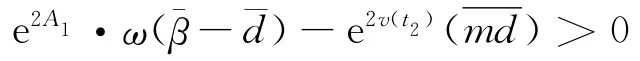
解这个不等式,得

或
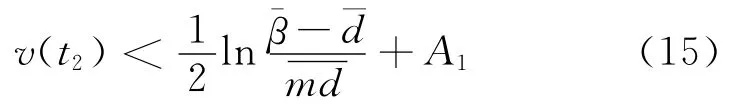
由(8)和(15)得
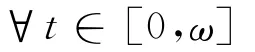
有

类似的,由式(6)、式(8)、式(10)和式(14)得


取
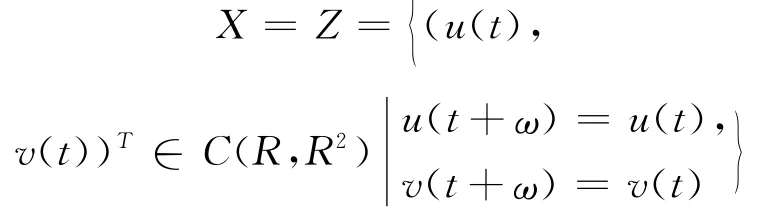
定义如下范数

则X是Banach空间。
令 L:domL X → X,L (u(t),v(t))T=(u′(t),v′(t))T,其中

再令N:X→X,则
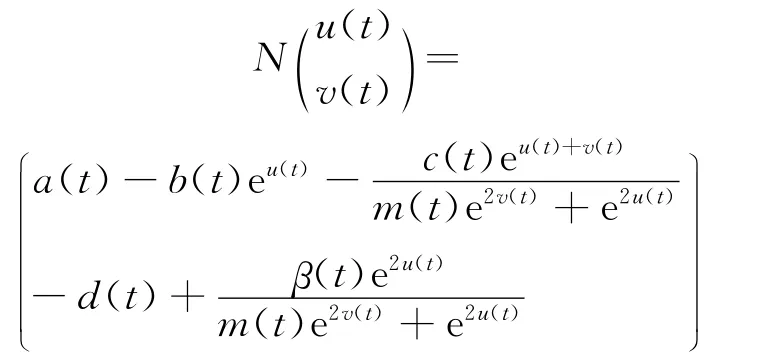
再定义两个投影P和Q,即
2) 修缮后的矿化床在前期(0~15 d) 对进水COD、NH3-N和TN均有较好的去除效果,COD最为明显,去除率>90%;随着运行时间的延长,去除效果呈下降趋势,推测由于矿化床靠微生物和吸附作用,受外界影响变化大,且易堵塞孔隙,极大影响矿化床的处理效果。
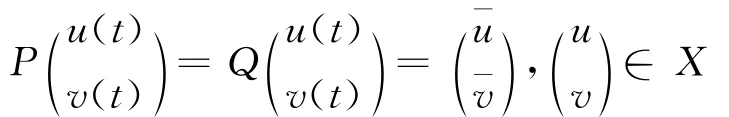
显 然,Ker L = ImP = R2,ImL = Ker Q ={(u(t),v(t))T∈X:u珔=v珔=0} 是X中的闭集,且dim Ker L =dim()=2。
因此,L是指标为零的Fredholm算子,又定义L的广义逆如下:

不难验证QN 和Kp(I-Q)N连续,取

由式(12)、式(14)、式(16)和式(17)可知

设
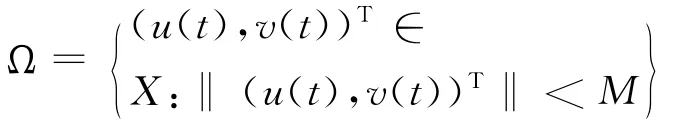
则Ω为X中的有界开集,根据Lebesgue控制收敛定理,可知QN和Kp(I-Q)N是连续的;进一步根据 Arzela-Ascoli 定 理 可 知 QN(Ω)和 Kp(I -Q)N(Ω)是紧集,因此,N 在Ω是L-紧的。
由式(12)、式(14)、式(16)、式(17)和式(18)可知,对 任 意 的 λ ∈ (0,1),(u(t),v(t))T∈ Ω ∩domL,都有L(u(t),v(t))T≠λN (u(t),v(t))T,即已经证明了引理中的条件(ⅰ)是满足的。
下面来证明引理中的条件(ⅱ)和(ⅲ)也是满足的。
设 (u,v)T∈Ω∩Ker L=Ω∩R2,即(u,v)T∈R2且 ‖ (u,v)T‖ = M 。
首先,证明QN (u,v)T≠0,即引理中的条件(ii)成立。若不然,即

由式(19)的第二式得
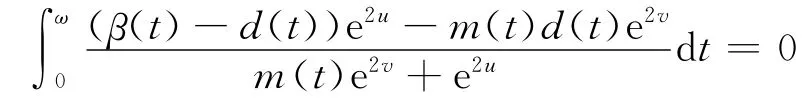
这可以推得
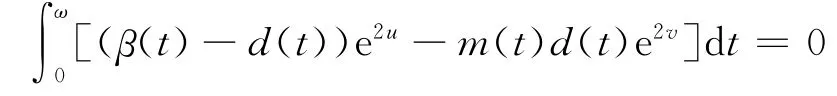
即
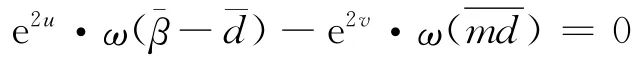
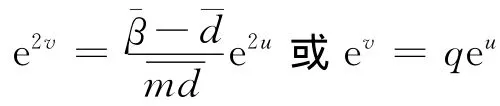
其中q为常数。代入式(19)的第一式可得

这和ev=qeu一起表明式(19)有唯一的解组(u,v)T,且
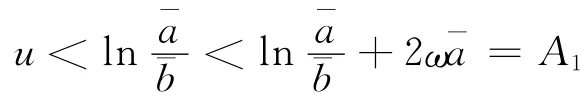
又类似于式(14)、式(16)、式(17)可证u>A2,v<B1,v>B2。因此

相矛盾,所以引理中的条件(ii)也是满足的。
最后,证明引理中条件(iii)也满足,为此,作同伦变换

其 中μ∈ [0,1]。Φ(u,v,μ)≠0。若Φ(u,v,μ)=0,则类似的可验证A2<u<A1,B2<v<B1,且Φ(u,v,μ)=0有唯一的解
进一步,令
J =I:ImL → Ker L,J (u,v)T= (u,v)T计算得

至此已经证明了对于有界开集Ω,引理中所要求的条件都是满足的,因此,系统(4)在Ω上至少存在一个ω-周期解,故系统(1)至少存在一个正的ω-周期解,定理得证。
推论 在系统(1)中,假设2aL>和βL>dM,则系统(1)至少存在一个正的ω-周期解。
证明由已知2aL>和βL>dM,得
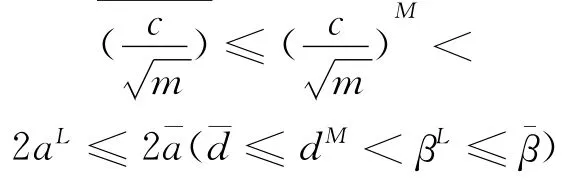
[1] Arditi R,Ginzburg L R.Coupling in predator-preg dynamics:ratio-dependence[J].Theor.Biol,1989(139):311-326.
[2] 马知恩.种群生态学的数学模型与研究[M].合肥:安徽教育出版社,1996.
[3] TIAN De-sheng,ZENG Xian-wu.Periodic solutions of a class of predator-prey model exploited with functional responses[J].J of Math(PRC),2005(25):480-484.
[4] Zhang Zhengqiu,Wang Zhichen.Periodic solution of a two-species ratio-dependent predator-prey system with time delay in a two-patch environment[J].Anziam J,2003,45:233-244.
[5] Tian Desheng,Zeng Xianwu.Existence of at least two periodic solutions of a ratio-dependent predator-prey model with exploited term[J].Acta Math.Appl.Sinica,English series,2005,23(03):489-494.
[6] Gaines R E,Mawhin J L.Coincidence degree and non-linear differential equations[M].Berlin:Springer,1977.

