齿轮传动副背隙动态测试平台的仿真与研究
王 刚,卢 红,石立城
(武汉理工大学机电工程学院,湖北 武汉430070)
当一对齿轮啮合时,轮齿非啮合面的两个轮齿之间存在回程间隙,这严重影响了传动精度和性能,为此,设计搭建一个传动性能测试实验台,主要分析比较可替换的行星齿轮传动和蜗轮蜗杆传动机构,测试研究机械传动系统的性能。齿轮传动和蜗轮蜗杆传动都是回转传动,在有些场合可以互换使用,但同时它们又各自具有自身的特点,在设计过程中需要根据实际的情况进行比较选择以保证传动形式最为可靠精准。目前研究现状是:两种传动方式的实验平台的振动、传动背隙、振动特性等属性不是特别清晰,内部规律还需进一步深入研究,本文以此为研究对象,用solidworks建模,使用有限单元法,比较了相同精度和尺寸大致相当条件下,这两种传动方式的一些模态、谐响应特性[1-2]。
1 蜗轮蜗杆和行星齿轮测试实验平台
本文设计建模,并用有限元分析为后续实验验证比较提供理论依据,并且将理论和实际进行匹配比较。为了比较齿轮传动系统与蜗轮蜗杆传动系统的差别,选取同样精度等级和相近大小尺寸的两套系统(图1、图2)。本实验用来比较两种传动方式在实际应用中的优劣,验证仿真的可靠性,为此搭建一个试验,实现方式为:驱动电机正转提供动力,负载电机被动反转模拟负载,具体通过加载试验,测试不同转速、转矩下传动系统振动、噪声等参数。通过噪声仪测量实验台的噪声分贝数来判断振动的强弱;在支架上粘贴应变片,测量应力变形情况来评估振动及其传动系统的稳定性。通过电气控制,使齿轮在起动和换向的过程中始终受到偏置力矩的作用,编码器读取脉冲反馈,半闭环控制,对误差进行实时补偿,实现无回差反转,从而达到消除背隙。检测比较传动机构随负载变化而变化的振动频率,传动精度,以及控制策略[3-4]。

图1 直线式布局

图2 垂直式布局
2 蜗轮蜗杆和行星齿轮接触应力分析
理论上没有背隙的齿轮应该也能传动,正因为齿轮在传动中会变形,才需要背隙。背隙与载荷关系曲线帮助用户判断加载之后的间隙与磨损,平衡取舍。而额定载荷下齿面变形量则可以反映由载荷造成背隙的影响,进而判断两种减速器的优劣。
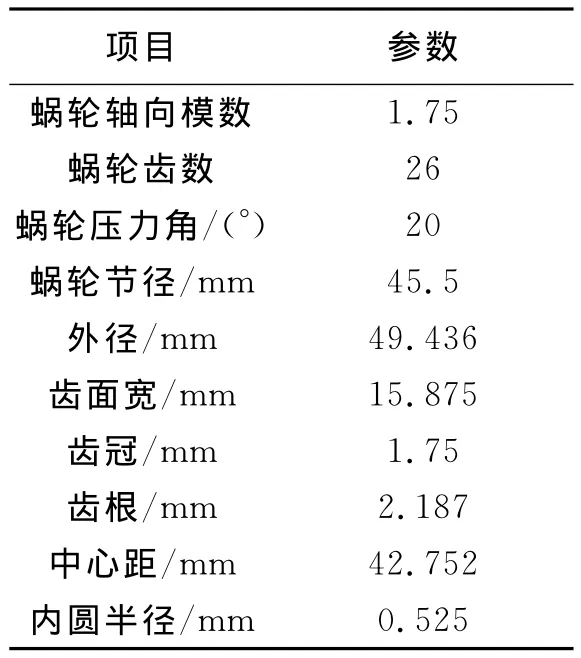
表1 蜗轮尺寸参数

表2 蜗杆尺寸参数
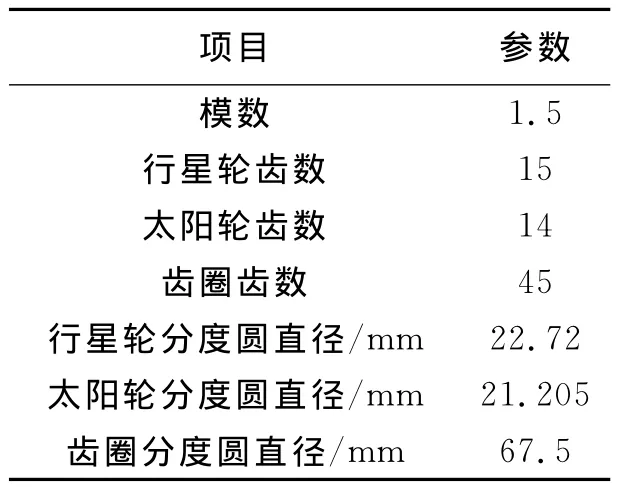
表3 星齿轮尺寸参数
在此,对以上蜗轮蜗杆[5-6](表1、表2)和行星齿轮[7-8](表3)进行了装配体导入、材料属性定义、边界接触条件定义、网格划分(见图3、图4)、施加约束、求解器定义等操作。其中材料为45号钢(调制),弹性模量E =200GPa,泊松比u=0.3;根据实际工况在蜗轮蜗杆和行星齿轮输入轴施加2.6 Nm转矩。

图3 蜗轮蜗杆网格划分

图4 行星齿轮网格划分

图5 蜗轮蜗杆等效应变
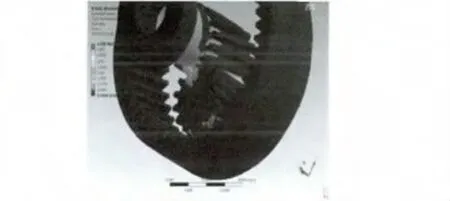
图6 行星齿轮等效应变
从图5、图6的应力应变云图可以分析出,在力矩传递过程中,齿廓之间会有很大的应力出现,但由于齿廓的强度较高,应变较小。然而每一个应变的叠加就会造成传动过程中的背隙出现,降低传动精度,引起振动和噪声,而且随着齿廓表面的磨损,背隙现象会越来越严重。
比较二者最大等效应变,行星齿轮明显小于蜗轮蜗杆。由此可以比较得出:无论从形变量,还是最大应力应变,行星齿轮都比蜗轮蜗杆性能优越;因此,由转矩产生的背隙,行星齿轮更少,性能更加优越。
3 模态分析
模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型,找到结构振动的一些基本振型对应的频率,避开这这些基本频率,防止共振。

表4 行星齿轮-蜗轮蜗杆一至六阶振型频率
从表4可以看出无论从各阶的振型还是变形量,行星齿轮减速器都比蜗轮蜗杆减速器优越,因为从结构上分析,行星齿轮为斜齿轮,并且对称性非常好,可以有效地削弱振动。
4 谐响应分析
谐响应分析建立在模态分析的基础之上,是用于确定线性结构在承受一个或多个随时间按正弦规律变化的载荷时,稳态响应的一种技术。谐响应分析的目的在于计算出结构在几种频率下的响应值对频率的曲线,从而使设计人员能预测结构的持续性动力特性,验证设计是否能克服共振、疲劳以及其他受迫振动引起的有害效果。
4.1 谐响应分析操作
从静态结构到模态分析到谐响应分析,材料属性和几何模型进行共享,并且对模型,设置,求解器进行设置。设置参数为:蜗轮蜗杆输入轴施加2.6 Nm转矩,蜗杆啮合面为检测平面,计算频率为从200Hz到4 000Hz,步长为50Hz;行星齿轮太阳轮输入轴孔中施加2.6Nm转矩,输出轴太阳轮轴为检测体,计算频率从4 000Hz到10 000Hz,步长为100Hz.
4.2 蜗轮蜗杆谐响应结果
图7为蜗轮蜗杆应力频谱和位移频谱。显然在频率为950Hz和2450Hz的时候,位移速度,应变和加速度有两个峰值。

图7 应力频谱(上)-位移频谱(下)
下面分别计算这两个频率值时候的位移形变和等效应应力。由图8可见:在950Hz的时候,蜗杆的谐响应振幅达到最大,为3.1964×10-5m,振动形式为蜗杆两端反向斜摆,最大振动位置发生在输入端;由图9可见:在2 450Hz的时候,蜗杆的谐响应振幅达到最大,为2.1688×10-4m,最大应力为6.688×108Pa,振动形式为蜗杆两端同向扭摆,最大振动位置发生在输出端;比较两图,第二种振动更加剧烈,与前面分析一致,并且容易引起齿轮箱体的严重振动。

图8 总体变形图1

图9 总体变形图2
4.3 行星齿轮谐响应结果
图10 为谐响应分析的应力频谱和位移频谱。显然在频率为4 600Hz和7 150Hz的时候,应力有两个峰值。
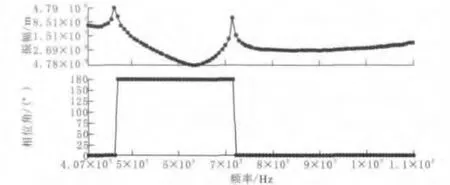
图10 应力频谱(上)-位移频谱(下)
1)分别计算这两个频率值时候的位移形变。由图11可以看出:在4 600Hz的时候,行星齿轮的太阳轮谐响应振幅达到最大,为1.7788×106m,最大应力为5.554×108Pa,振动形式为太阳轮轴向串动,最大振动位置发生在太阳轮齿轮啮合处。
2)由图12可以看出:在7 150Hz的时候,行星齿轮的太阳轮的谐响应振幅达到最大,为7.927×104m,最大应力为4.257×109Pa,振动形式为太阳轮回转振动,最大振动位置发生在齿轮啮合处。

图11 总体变形1

图12 总体变形2
5 结论
1)应变的叠加就会造成齿侧背隙,降低传动精度,而且随着齿廓表面的磨损,背隙现象会越来越严重;无论从形变量,还是最大应力应变,行星齿轮都比蜗轮蜗杆性能优越。
2)行星齿轮减速器振动频率比蜗轮蜗杆高,远离正常工作频率,并且抗振动效果比蜗轮蜗杆减速器好;在机器正常工作频率区间,要远离计算出的峰值频率,启动的时候不能长期停留在振动加强频率区间,正常工作时要选择振动比较低且比较平稳的工作频率区间。根据理论频率曲线和对应振型可以提前预知实际振动形式,为搭建实验平台提供了数据。
[1] 常 远,甄万才.齿轮传动与蜗轮蜗杆传动性能比较与消隙机构[J].电子工业专用设备,2007(01):1-3.
[2] Baek J.Backlash estimation of a seeker gimbal with two-stage gear reducers[J].The International Journal of Advanced Manufacturing Technology 21.8(2003),2003,1(01):1-2.
[3] Merzouki R,CadiouandN J C.Sirdi M.Compensation of backlash effects in an Electrical Actuator[J].LaboratoiredeRobotiquedeVersailles 10-12,avenue de l’Europe.2:2-3.
[4] 王汝青,陈兴燕,卢 利.基于ANSYS的非对偶蜗轮蜗杆不同啮合位置有限元分析[J].科技广场,2012(05):6-9.
[5] 邱 晶 .基于ANSYS环境下的TI蜗杆建模分析与安装误差分析[D].天津:天津大学,2006.
[6] 李俊源.基于SolidWorks的蜗轮蜗杆三维参数化设计[J].长春理工大学学报,2006,29(01):2-3.
[7] 刘雪艳.基于ANSYS的渐开线直齿行星齿轮有限元分析[D].西安:西北农林科技大学,2009.
[8] 王春光.行星齿轮传动动态特性的研究[D].哈尔滨:哈尔滨船舶锅炉涡轮机研究所,2005.

