基于k－壳分解的集装箱海运网络度分布研究＊

王 杰 王晓斌

（大连海事大学交通运输管理学院 大连 116026）

0 引 言

海运网络是一个综合、开放、动态的复杂系统，以往相关研究主要集中在图论、分形理论等方法上，主要围绕海运网络的空间组织与优化、经济效率等进行分析，缺乏其整体性和规模性的研究．复杂网络理论对此提供了新的重要思路．

目前，针对海运网络的复杂性研究尚处于起步阶段．Fremont［1］以马士基班轮公司的数据为例，构建了全球海运网络，对其航线结构、港口情况及发展演变趋势进行了详细分析；熊文海［2］从复杂网络理论出发，对世界海运网络的结构特性及其动力学行为进行了深入探讨；武佩剑等［3］验证了集装箱海运网络的小世界特性和无标度特性，得出度较大的节点对集装箱海运网络影响较大的结论；王成金［4］剖析了全球集装箱航运组织网络的空间格局和主要港口的集装箱组织能力；陈关荣［5］介绍了近年来复杂网络研究新领域；覃森等［6］对节点数固定的复杂网络进行了初步探讨．

综之，以往研究多认为海运网络具有无标度分布特性．本文运用k－壳分解法（k－shell decomposition）研究东亚区域集装箱海运网络，得出不同于以往的网络分布特性，并分析其原因．

1 复杂网络基本理论概述

近10a来，复杂网络理论研究取得了巨大进展［7－13］，形成庞大的体系．在此仅选取与本研究相关的基本理论进行介绍．

1．1 网络模型

复杂网络研究涉及的网络模型包括全局耦合网络模型、最近邻耦合网络模型、星形耦合网络模型、随机图模型、配置模型、BA无标度网络模型等，其中全局耦合网络模型和星形耦合网络模型与本研究直接相关．

1）全局耦合网络 如果一个网络中任意2个节点之间都有边直接相连，那么就称该网络为一个全局耦合网络，简称全耦合网络，见图1．

2）星形耦合网络 如果一个网络有且仅有一个中心节点，其余的节点都只与这个中心节点连接，而他们彼此之间不连接，那么称该网络为星形耦合网络，见图2．

图1 全耦合网络

图2 星形耦合网络

1．2 网络度及度分布

在网络中，节点的度是指与之相关联的边的条数，而度分布p（k）表示随机选取一个节点其度值为k的概率．即

式中：Nk为网络中度为k的节点个数；N为节点总数．

1．2．1 无标度分布

如果一个分布p（k）不存在明显的特征标度则称网络服从无标度分布，即不存某个特征标度使大部分取值都落在以特征标度为中心的一个相对较小的区域内．

1．2．2 幂律分布

若存比例在常数C和幂指数γ，使得近似有

则称该网络度分布为幂律分布．幂律分布是惟一满足无标度分布的概率分布函数．

并且由p（k）＝Ck－γ⇒ln p（k）＝ln Ck－γ⇒lnp（k）＝ln C－γln k，可知在双对数坐标下ln k～ln p（k）近似成负相关．

1．3 k－壳分解法

针对复杂网络的各种基础性研究中，寻找网络中最具影响力的中心节点始终是一个重要问题，k－壳分解法就是寻找网络中心节点的有效手段，具体算法如下．

1）将所有度值为1的节点，以及与这些节点相连的边从网络中移除，同时将因此产生的新的度值为1的节点及其连边从网络中移除，迭次重复，直到网络的剩余节点度值均大于1为止．将移除的节点和边作为网络的1－壳，且其ks值为1．

2）将网络中度值为2的节点以及与这些点相连的边从网络中移除，并且将因此产生的度值小于2的节点及其连边从网络中移除，迭次重复，直到网络的剩余节点度值均大于2为止．将移除的节点和边作为网络的2－壳，且其ks值为2

3）重复前2步，直到网络中所有节点都被划分到一个相应的k－壳中，即可获得该网络的k－壳分解．

得到k－壳分解后，网络中每一个节点都拥有属于自己的惟一ks值，所有ks值大于或等于k的节点称为该网络的k－核（k－core）．

2 东亚集装箱海运网络实证分析

2．1 数据来源及说明

本文以世界排名前3的马士基、地中海航运和达飞公司为背景，整理出东亚区域的主要集装箱航线；3大班轮公司在东亚区域共有72条航线，涉及47个港口．港口编号见表1．

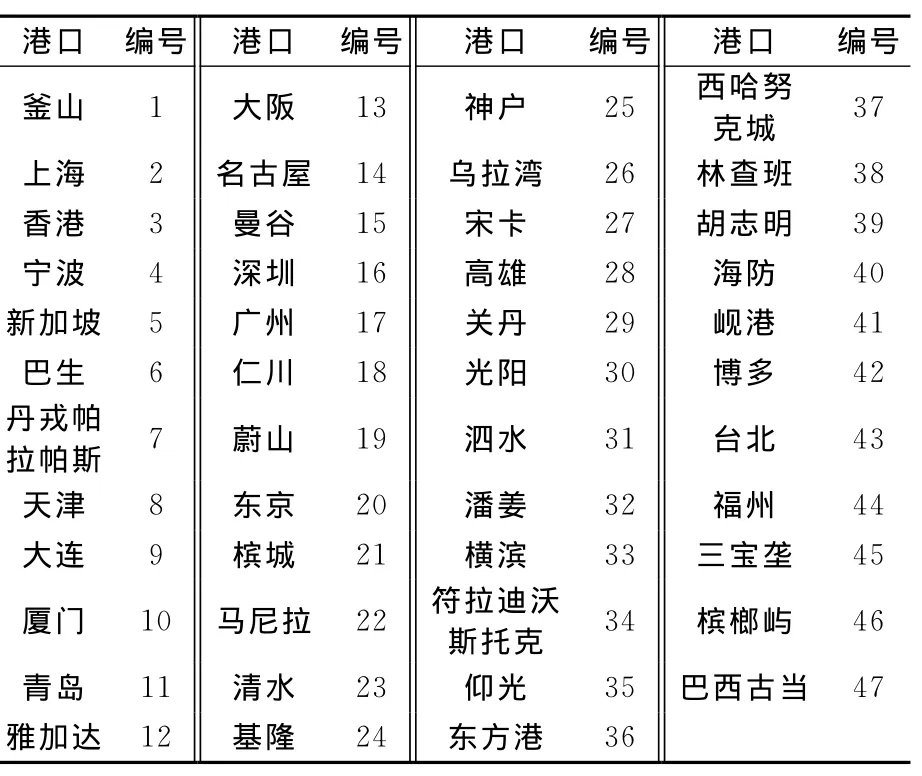
表1 港口编号

2．2 基于k－壳分解的网络实证分析

运用前述k－壳分解法分解上述网络，可知该网络节点共分5层，各层节点编号如下：ks＝1，包括34，35，36，43，44编号节点；ks＝2，包括15，23，26，27，29，41，45，46，47编号节点；ks＝3，包括19，21，32编号节点；ks＝4，包括9，18，20，37，40，42编号节点；ks＝5，包括1，2，3，4，5，6，7，8，10，11，12，13，14，16，17，22，24，25，28，30，31，33，38，39编号节点．

经计算，原始网络（1－核）涉及的港口度值见表2，网络度分布见表3．

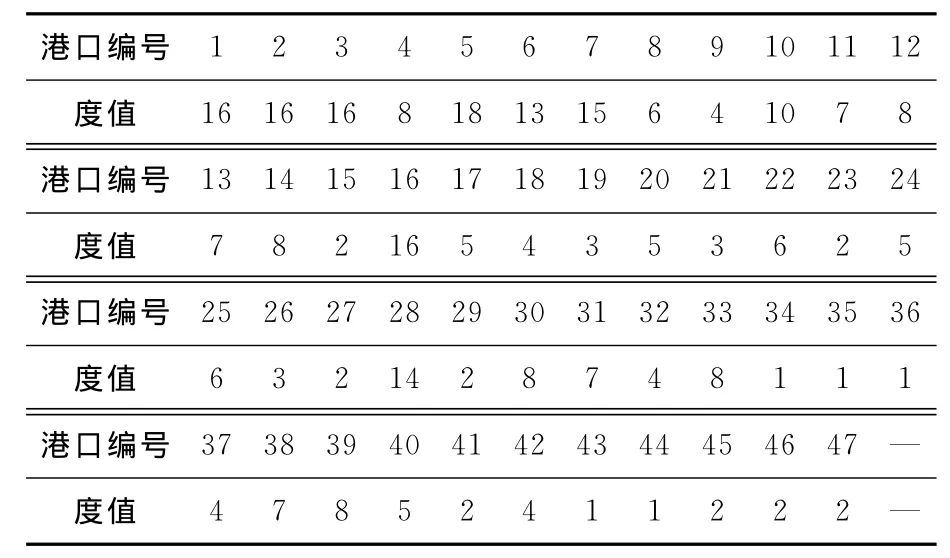
表2 1－核网络度值

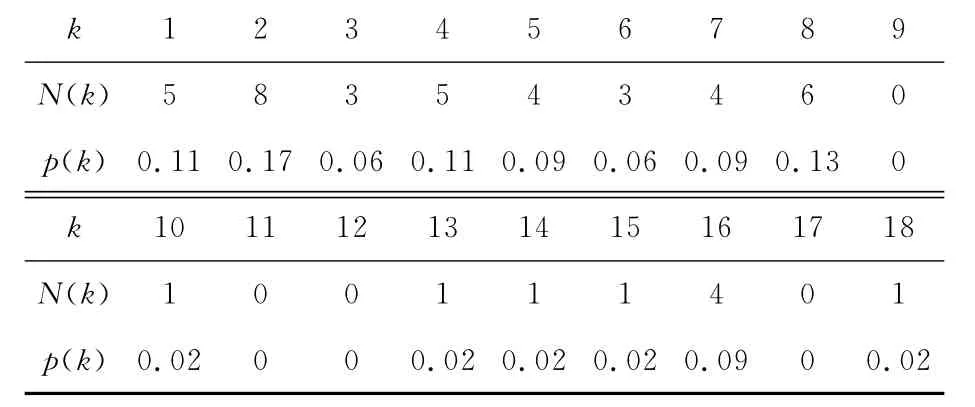
表3 1－核网络度分布

分别在普通坐标和双对数坐标下绘制该网络的度分布图，见图3．

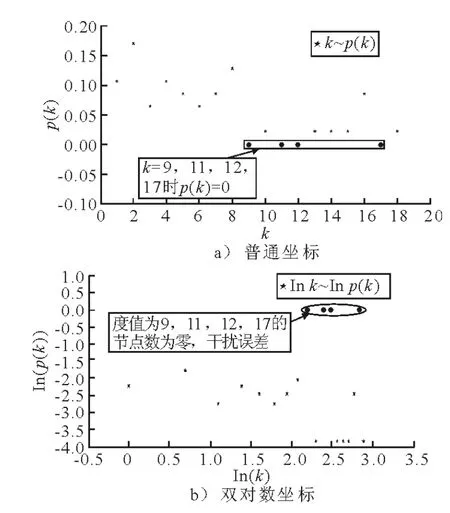
图3 节点度分布

其中，度值为11，12，17的节点（图中圆点）个数N（k）＝0，其概率分布p（k）＝0，双对数坐标下lnp（k）＝ ∞ ，为干扰项．

移除该网络的1－壳，得到该网络的2－核子网络，经计算2－核网络的港口度值见表4，网络度分布见表5．普通坐标和双对数坐标下2－核网络的节点度分布见图4．

同理，可得到该网络的3－核子网络，经计算3－核网络的港口度值见表6，网络度分布见表7．普通坐标和双对数坐标下3－核网络的节点度分布见图5．

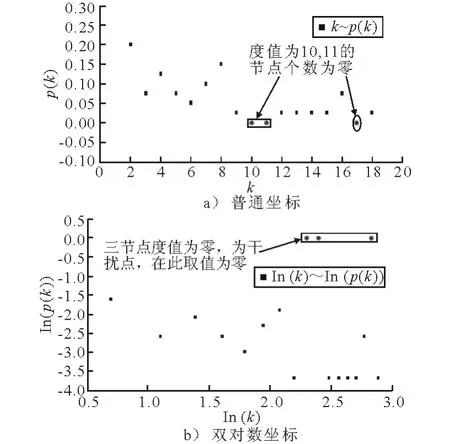
图4 节点度分布

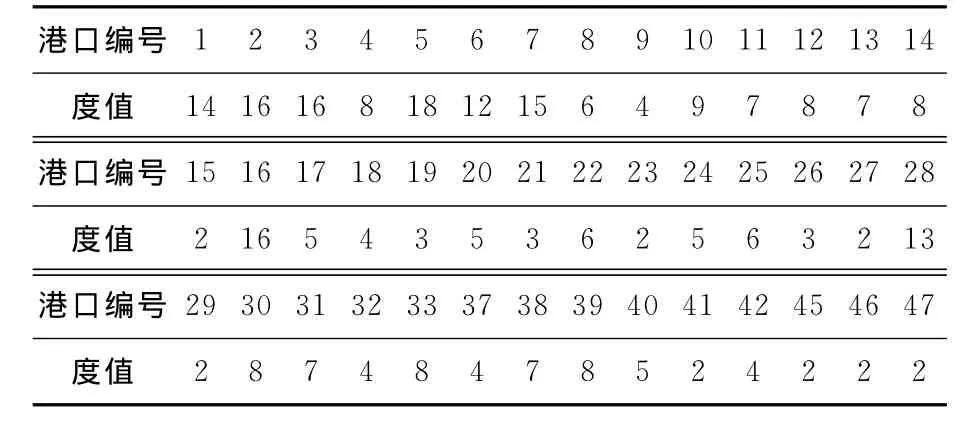
表4 2－核网络度值

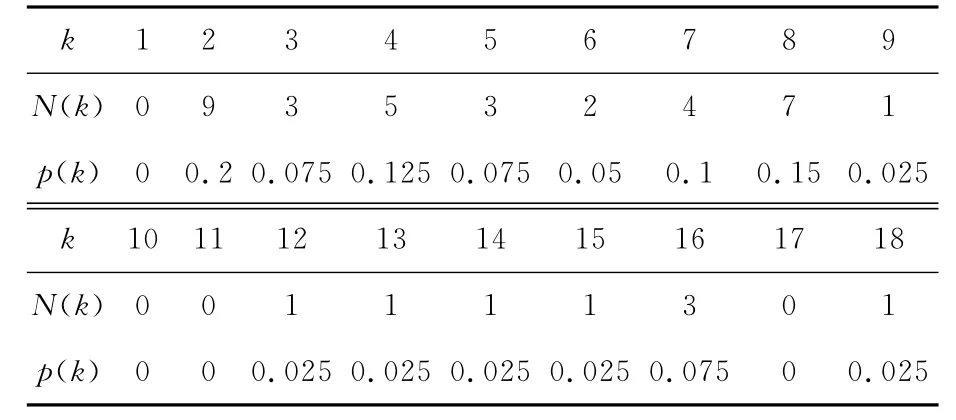
表5 2－核网络度分布

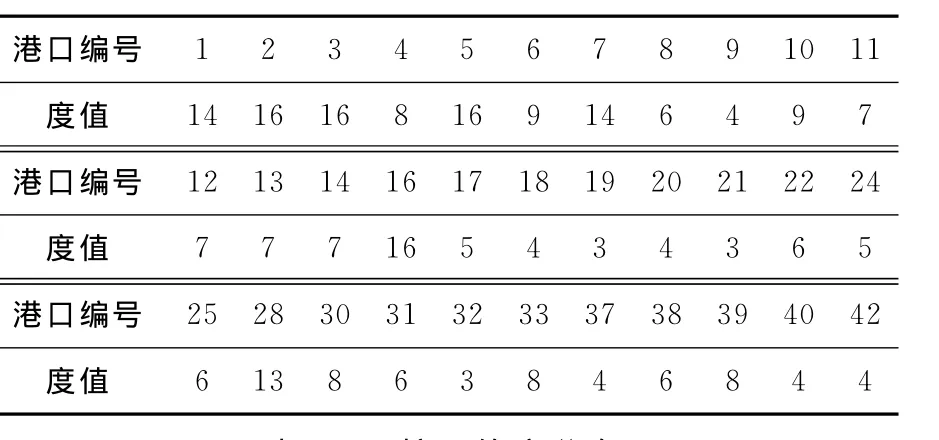
表6 3－核网络度值

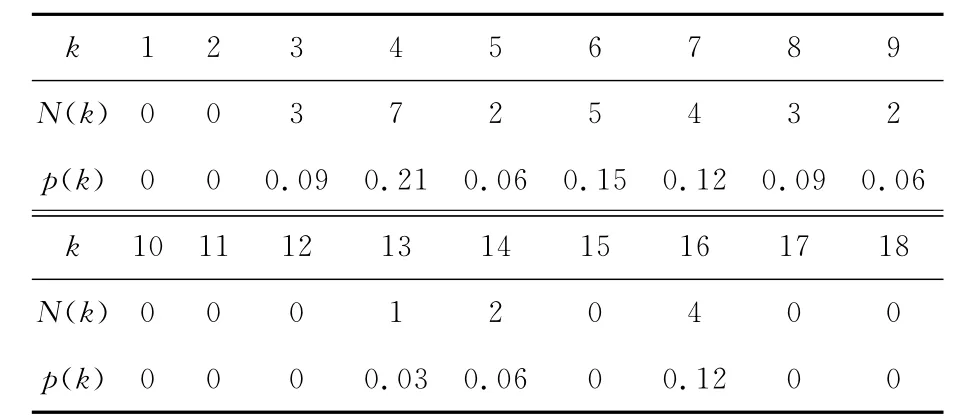
表7 3－核网络度分布

同理，可得到该网络的4－核子网络，经计算4－核网络的港口度值见表8，网络度分布见表9．普通坐标和双对数坐标下4－核网络的节点度分布见图6．

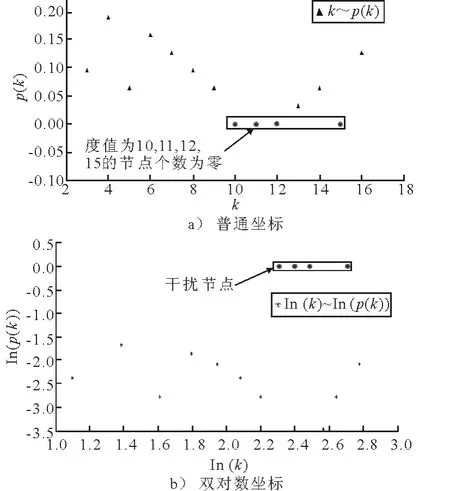
图5 节点度分布

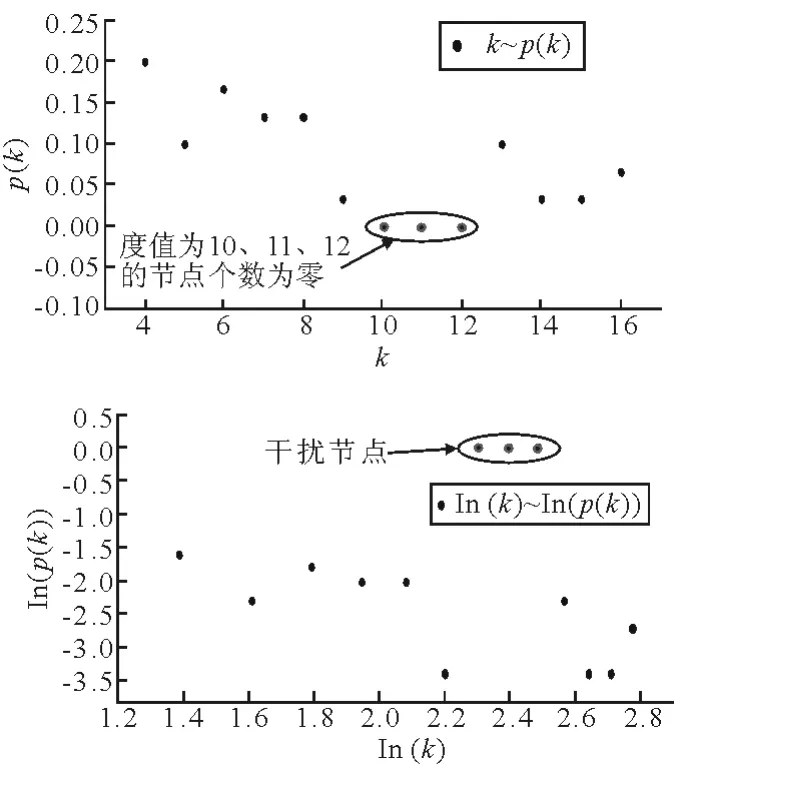
图6 节点度分布

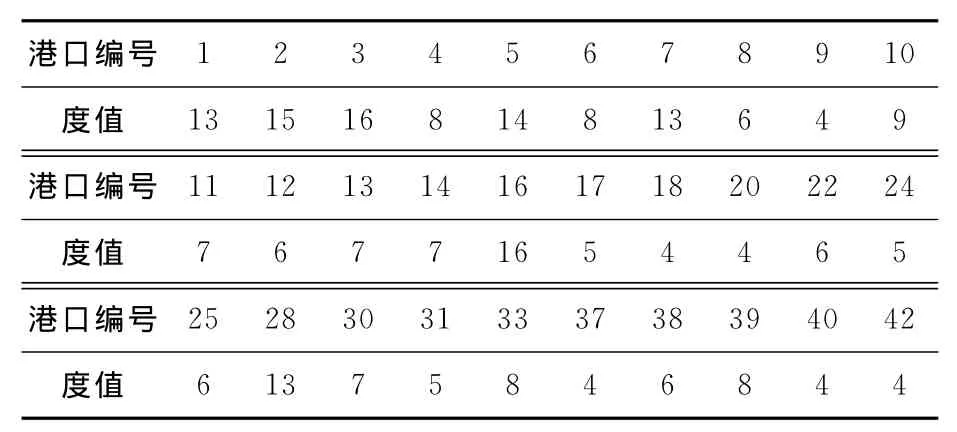
表8 4－核网络度值

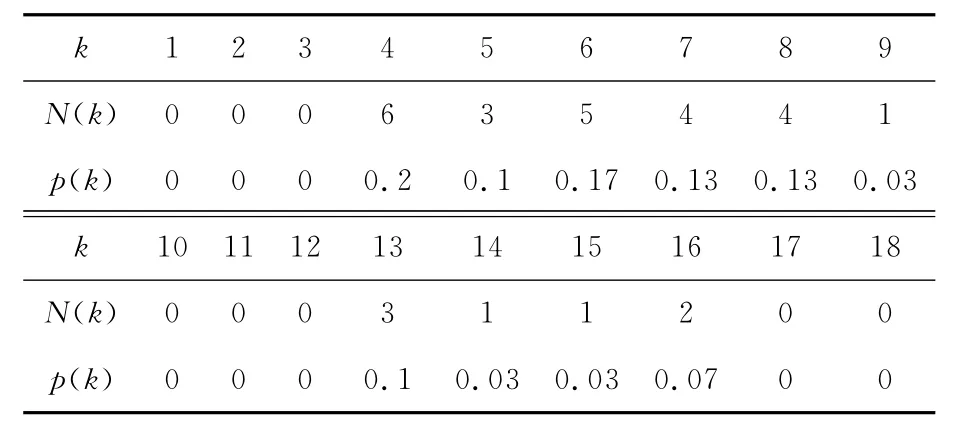
表9 4－核网络度分布

同理，可得到该网络的5－核子网络，经计算5－核网络的港口度值见表10，网络度分布见表11．普通坐标和双对数坐标下5－核网络的节点度分布见图7．

表10 5－核网络度值

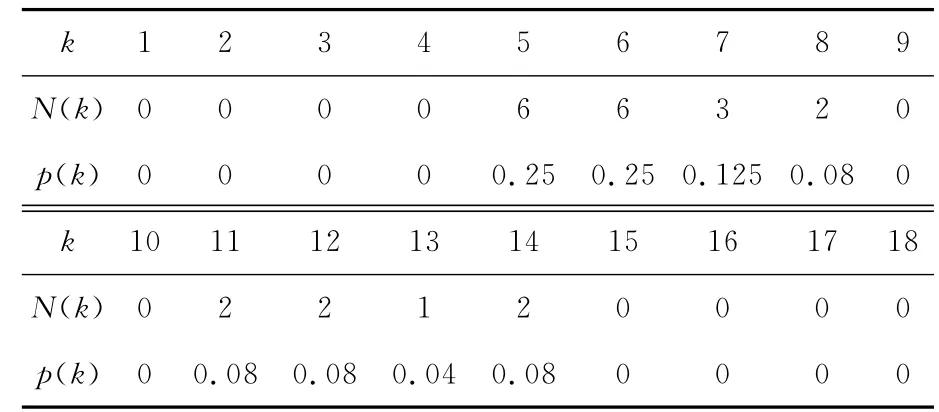
表11 5－核网络度分布

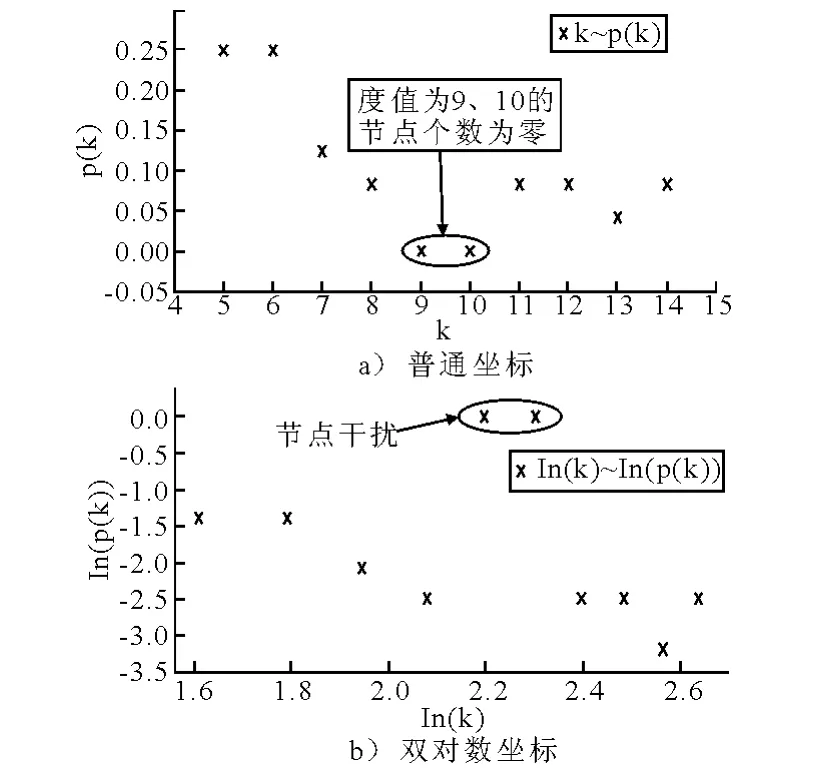
图7 节点度分布

2．3 实证分析结果及其原因分析

由图3a）～图7a）可见，在普通坐标下，去除干扰节点后，可以明显将图中黑点分成若干部分，即实际网络的度值存在若干特征标度．这种现象在图3a），5a），6a）中表现为2个特征标度，在图7a）中表现为3个特征标度．

进一步地，由图3b）～图7b）可以看出，在双对数坐标下，ln k～ln p（k）之间也不存在明显的负相关性；而在以往关于海运网络分布的研究多认为网络度分布具有无标度特性，由附录一可知无标度网络近似服从幂律分布，且在双对数坐标下表现为明显的负相关．

鉴此，得出以下结论，东亚区域集装箱海运网络并非无标度分布，f（x）并不能近似表示成式（2）的形式；实际网络中既存在大量度值相对较小的节点，也存在相当一部分度值相对较大的节点，而度值适中的节点则相对较小，亦即从度值大小的角度看，网络中节点存在分层．

根据集装箱运输的实际情况，海运网络度值分层原因有如下3点．

1）为增强海运网络的鲁棒特性而有意设计一些“圈”．这类情况普遍存在于各类技术网络中（Intenet网络和公路网络等），目的是当网络受到外力冲击时仍能维持基本的通信能力．这样便形成了网络中最核心的一部分节点，它们构成一个全局耦合网络，见图8．

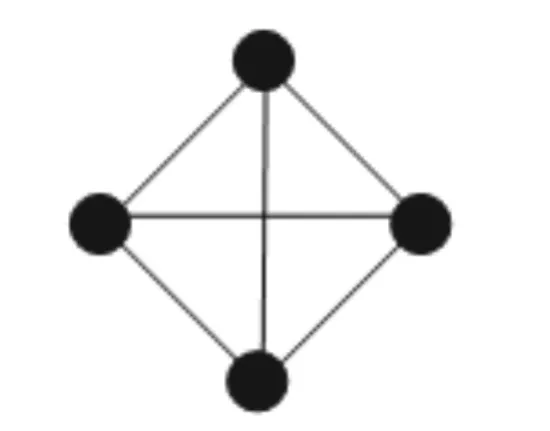
图8 枢纽港间连接

2）从节约成本的角度，集装箱运输多采用轴辐式运输模式．这样便形成支线港与核心港的连接，它们构成星形耦合网络，见图9．

3）出于行业竞争和追求跨越式发展，网络中出现一些零星连接，在图上表现为支线港与核心港间的随机连接，见图10．

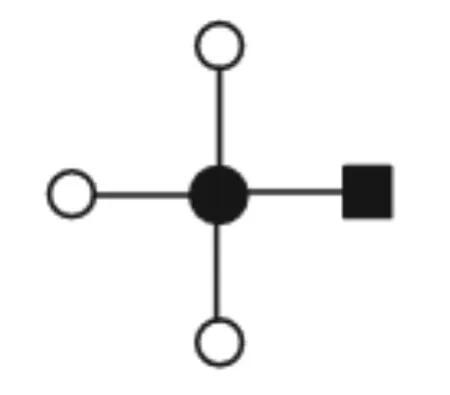
图9 支线港与枢纽港间连接

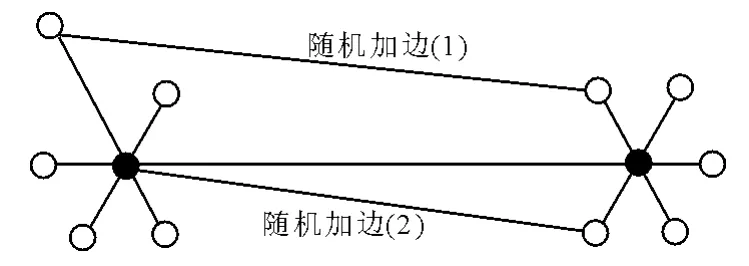
图10 理论模型

3 结 论

1）基于概率理论，证明无标度网络必定具有近似幂律形式分布函数，且其在双对数坐标下近似负相关．

2）基于东亚区域集装箱海运数据，计算集装箱海运网络度分布．在普通坐标下，可以观察到节点度值具有明显的分层现象；在双对数坐标下，并未观察到ln k～ln p（k）间具有显著负相关性，可见集装箱海运网络度分布不能近似用幂律函数形式表示．

3）结合东亚集装箱海运的实际情况，将该区域海运网络节点度值分层的原因归结为鲁棒性、经济型和竞争性，并给出其网络拓扑解释．

［1］FREMONT A．Global maritime networks：the case of Maersk［J］．Journal of Transport Geogra－phy，2007，15：431－442．

［2］熊文海．世界航运网络的结构特性及其动力学行为研究［D］．青岛：青岛大学，2008．

［3］武佩剑，邓贵仕，田 炜．集装箱航运网络拓扑特性研究［J］．武汉理工大学学报：交通科学与工程版，2008，32（4）：665－668．

［4］王成金．全球集装箱航运的空间组织网络［J］．地理研究，2008，27（3）：636－647．

［5］陈关荣．复杂网络及其新近研究进展简介［J］．力学进展，2008，38（6）：653－662．

［6］覃 森，戴冠中，王 林．节点数固定的复杂网络模型初探［J］．复杂系统与复杂性科学，2005，2（2）：7－11．

［7］汪小帆，李 翔，陈关荣．网络科学导论［M］．北京：高等教育出版社，2012．

［8］何大韧，刘宗华，汪秉宏．复杂系统与复杂网络［M］．北京：高等教育出版社，2009．

［9］王 林，戴冠中．复杂网络的Scale－free性、Scale－free现象及其控制［M］．北京：科学出版社，2009．

［10］AIRRIESS C A．The spatial spread of container transport in a developing regional economy［J］．Transportation Research，1989（6）：453－461．

［11］BAIRD A J．Rejoinder：Extending the lifecycle of container main ports in upstream urban locations［J］．Maritime Policy ＆ Management，1979（2）：299－301．

［12］NOTTEBOOM T E．Concentration and load centre development in the European container port system［J］．Journal of Transport Geography，1997（2）：99－115．

［13］庄佩君．全球海运物流网络中的港口城市－区域：宁波安例［D］．上海：华东师范大学，2011．