基于盲数理论的我国海上战略通道安全风险评价＊

李振福 颜章龙

（大连海事大学交通运输管理学院 大连 116026）

由于经济的快速发展，中国经济正在遭遇资源和能源的瓶颈，要实现中国经济的可持续发展，就必须把眼光投向海外，谋求国际资源和世界市场［1－2］．所以，利用海上通道进行运输是一个非常重要的战略问题．海上战略通道的安全面临着传统安全因素和非传统安全威胁的风险［3］．我国海上战略通道的安全性研究，目前是一个热点问题．由于通道的安全风险评价信息具有未确知性，并且是盲信息，因而本文利用盲数理论［4］对通道的安全风险进行评级，为解决这一难题提供了一种方法．

1 盲数理论

1．1 盲数的概念

设R为实数集，R为未确知有理数集，G是有理灰数集．

设ai∈G，αi∈ ［0，1］，i＝1，2，…，n，f（x）为定义在G上的灰函数称为A与B的可能值带边 ＊ 矩阵，x1，x2，…，xm和y1，y2，…，ym分别表示A与B的可能值序列，互相垂直的2条直线叫纵轴和横轴，第一象限元素构成的m×n阶矩阵称为A与B在＊运算下

若当i≠j时，ai≠aj，且 ＝α，0＜α≤1，则称函数f（x）是一个盲数，阶数为n．称αi为f（x）在ai的可信度，称α为f（x）的总的可信度［5］．

1．2 盲数的运算

设＊表示G中的一种运算，可为＋，－，×或÷中的任一种．

设盲数的可能值＊矩阵，简称可能值＊矩阵．称为A 关于B 的可信度带边积矩阵，α1，α2，…，αm和β1，β2，…，βm分别表示A与B的可信度序列，第一象限元素构成的m×n阶矩阵称为A关于B的可信度矩阵，简称可信度积矩阵［6］．

称φ（x）为盲数A与B的＊运算，记作

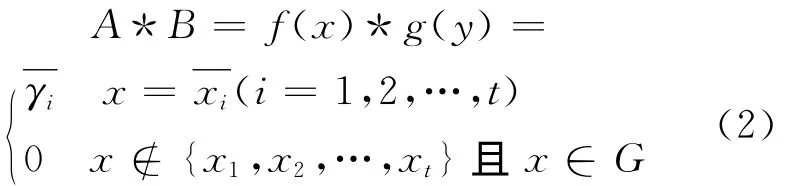
式中：在进行除法运算时要求yj（j＝1，2，…，n）的区间中不包含有零．

设A，B，C是盲数，则盲数的运算具有下列性质：（1）A＋B＝B＋A；（2）A×B＝B×A；（3）（A＋B）＋C＝A＋（B＋C）；（4）（A×B）×C＝A×（B×C）．

2 通道评价的盲数模型

2．1 通道单因素的未确知测度

在通道的安全风险评价中，对安全风险产生影响的因素主要是定性指标，其确定采用德尔菲法（Delphi），由若干专家进行评价．

专家可信度，即为专家的可信赖程度，某些程度上体现了专家在该领域的权威．最值得信任的专家可信度为1，最不值得信任的专家可信度为0，若专家组A1，A2，…，An的可信度分别为，

称为专家Ai关于专家组A1，A2，…，An的综合可信度［7］．

设C＝ ｛c1，c2，…，cK｝为评价空间，其中ck（1≤k≤K）为第k个评价等级．现将评价中的ai1，ai2，…，ain按不同分数重新排列为：aij1，aij2，…，aijk，αijk为x＝aijk时的专家可信度之和．于是，对于因素Ai可得盲数fi（x）：

设影响海上战略通道安全有n个因素F1，F2，…，Fn，记为F ＝ ｛F1，F2，…，Fn｝．用xi表示在Fi因素下的评价值．设评价值xi处于第k个评价等级ck的程度为αik＝α（xi∈ck），那么αik是对程度的一种测量结果，其满足3条测量准则，即非负有界性、可加性、归一性：（1）0≤αik≤1；

式中：其中：i＝1，2，…，n；k＝1，2，…，K．称满足上述3条测量准则的αik为未确知测度．称

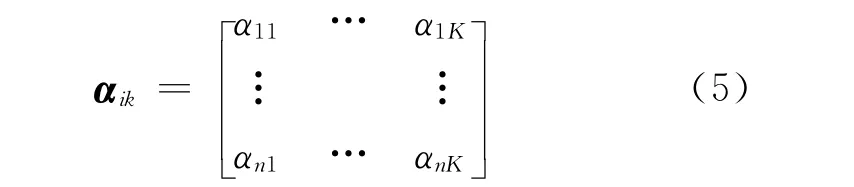
为单因素评价矩阵．

2．2 因素权重的确定

本文采用层次分析法（AHP）确定因素的权重，通过对n个因素成对比较，构造一个反映两两之间重要程度的判断矩阵．

判断矩阵分析法，是把m个评价因素排成一个m阶判断矩阵，专家通过相对比较标度（见表1），对因素两两比较，得到判断矩阵

表1 相对比较标度

求解判断矩阵B的最大特征根λmax及其对应的特征向量ξ＝ （ξ1，ξ2，…，ξn），进行一致性检验，其中RI的取值见表2．

表2 RI取值

当CR≤0．1时，判断矩阵基本符合一致性条件；当CR≥0．1时，认为所给出的判断矩阵不符合一致性条件，需要进行修正判断矩阵的元素．

取ξi作为因素Fi的权重，必要时可以对特征向量ξ进行归一化处理，从而得到所求的盲数模型各个因素的权重向量：

2．3 多因素综合未确知测度分析

根据通道的单因素未确知测度αik和各因素的权重向量ξ，可以计算出通道多因素综合未确知测度α：

2．4 评价准则的确定

由于通道安全评价的评价目标取值为安全风险越小越好，并且评价的各个等级间有c1＜c2＜…＜cK，即评价等级划分是有序的，所以不能使用最大测度识别准则进行评价，适合用置信度识别准则代替．由于评价空间存在有序性和信息不确定性，为了使评价结果更加合理，设置信度为λ（λ＞0．5），通常取0．6或0．7［8－10］．

令：

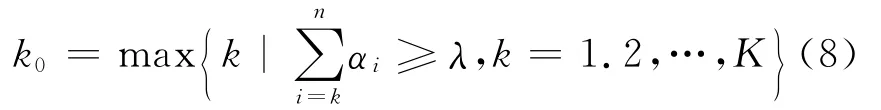
则判定通道属于第k0个评价等级ck0．

3 案例分析

以我国一个战略通道——马六甲海峡为例，利用盲数理论对马六甲海峡通道进行安全风险评价和分析．

马六甲海峡目前由新加坡、马来西亚和印度尼西亚3国共同管理．一旦马六甲海峡形式紧张，一些大国介入其中，封锁海峡，将直接影响中国进出口运输的安全，也关系着中国未来的发展和安全［11］．

通过分析，得到影响马六甲海峡的安全因素主要如表3所列．

表3 影响马六甲海峡的安全因素

建立评价空间C．在对马六甲海峡进行安全风险分析时，将马六甲海峡的通道安全性分为5个等级，即c1，c2，c3，c4，c5，分别表示非常安全、安全、普通、危险、非常危险．评价空间C记为：C＝｛c1，c2，c3，c4，c5｝，且有ci∩cj＝ ∅（i，j＝1，2，3，4，5且i≠j），实际上，认为ck＋1比ck“危险程度高”，记为ck＋1＞ck（k＝1，2，3，4）．

由5位专家对马六甲海峡通道安全的因素实施评价，专家的具体情况如表4所列，并由式（3）取得专家的综合可信度值．按非常安全（1分），安全（2分），普通（3分），危险（4分），非常危险（5分）进行打分评价，评价结果见表5．

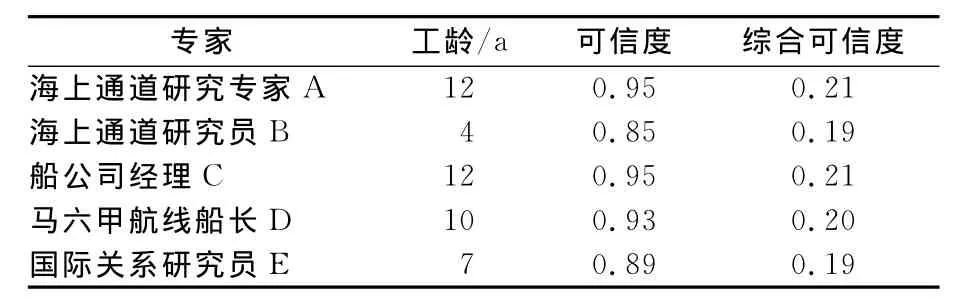
表4 评价专家情况

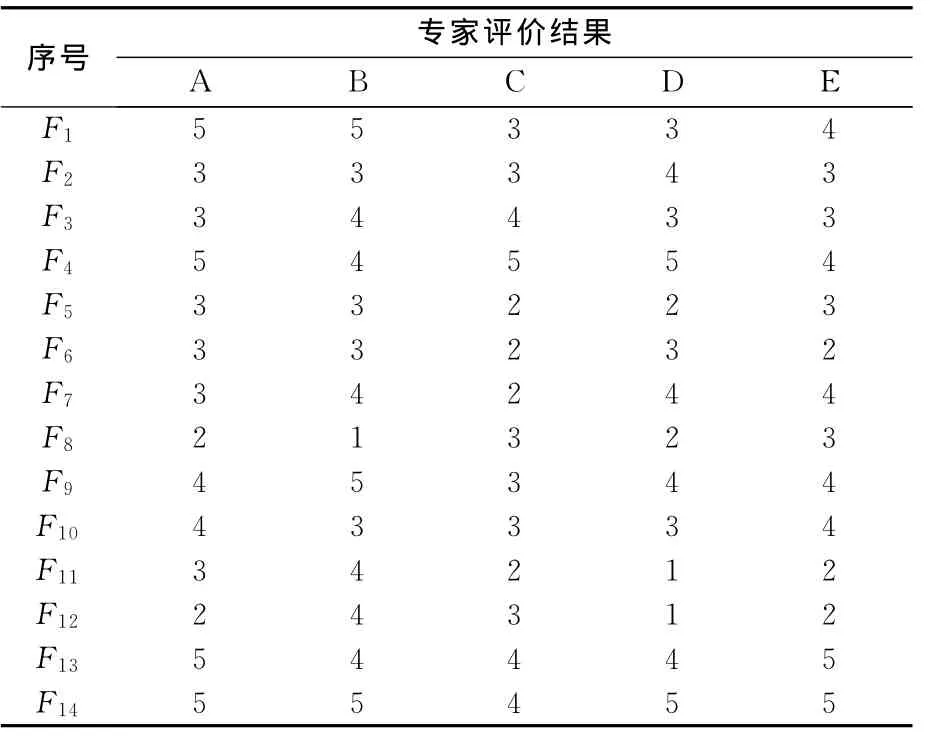
表5 影响马六甲海峡通道安全因素的专家评价

设 f1（x），f2（x），…，f14（x）为 F1，F2，…，F14的综合评价值，由公式（4）则可知f1（x），f2（x），…，f14（x）为盲数，表示如下．

用ν表示影响马六甲海峡通道安全因素的单指标未确知测度评价向量，根据盲数理论，由式（5）有

通过对这14个影响因素进行两两比较，构造了一个反映两两之间重要程度的判断矩阵如表6．利用数学计算Matlab工具调用AHP算法求得影响马六甲海峡的14个因素的权重见表7．

随机一致性比率CR＜0．10时，判断矩阵才具有满意的一致性．否则，需要对判断矩阵进行调整，直到满足一致性条件．在本例中，

表6 基于AHP的属性层权重确定

表7 各因素的权重

说明所获得的指标权重值比较合理，可以作为分析结果用于评价研究．

对马六甲海峡安全风险评价的未确知测度α定义为

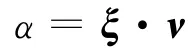
式中：ξ为影响马六甲海峡通道安全的14个因素的权重；ν为14个因素的单指标测度．这里

从而由式（7）可以求得，

若取置信度为λ＝0．7，按式（8）即可求得马六甲海峡的评价等级的k0值：

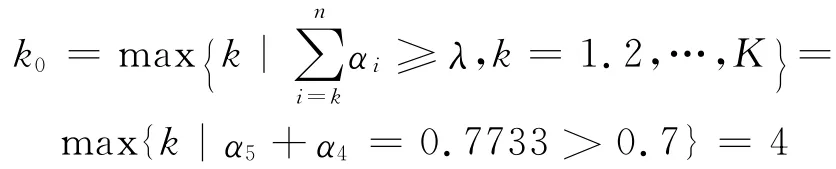
从而马六甲海峡的评价等级为c4，即马六甲海峡的通道安全风险级别为：危险．

设置信度为λ＝0．6，则可求得马六甲海峡的评价等级的k0值：

即马六甲海峡的评价等级为c4．同样地，在该置信度水平下，马六甲海峡的通道安全风险级别为：危险．

4 结束语

本文应用盲数理论，探索了一种将海上战略通道的研究从定性研究到定量研究的方法，提出了一个对海上通道进行安全风险评价的模型，为通道的研究提供一个新的视角．根据该模型，研究人员可以对我国海上战略通道的安全风险性能做出评估和预测．本文以马六甲海峡为例进行了安全风险评价，研究结果表明，将盲数理论用于通道安全风险的评价，具有一定的理论可行性和推广应用价值．

［1］李 兵．海上战略通道安全透视［J］．人民论坛，2010（1）：36－37．

［2］王历荣．论中国海上通道安全［J］．徐州工程学院学报：社会科学版，2009，24（5）：10－13．

［3］谭 箭，胡国龙．海事非传统安全现状分析［J］．武汉理工大学学报：交通科学与工程版，2012，36（3）：624－627．

［4］刘开第，吴和琴，庞彦军，等．不确定信息数学处理及应用［M］．北京：科学出版社，1999．

［5］王宝森，公 平，郑丕谔．盲数在投资项目经济评价中的应用［J］．河北建筑科技学院学报，1999，16（2）：59－61．

［6］刘开第，吴和琴，庞彦军，等．盲数的概念、运算与性质［J］．运筹与管理，1998，7（3）：14－17．

［7］王岳峰，刘 伟．信息混沌环境下区域物流能力盲数测评模型［J］．管理学报，2010，7（3）：418－422．

［8］刘开第，庞彦军，姚立根，等．大气环境质量评价的未确知测度模型［J］．环境科学，2000，21（3）：11－15．

［9］刘开第，庞彦军，孙光勇，等．城市环境质量的未确知测度评价［J］．系统工程理论与实践，1999（12）：52－58．

［10］吴彩华，刘开第．大气环境质量评价的未确知测度模型［J］．河北建筑科技学院学报，1999，16（3）：81－85．

［11］胡利明，周山丹，冯 丹．马六甲海峡与中国石油运输安全［J］．价值工程，2010（35）：44－45．