变压器套管容性故障对频响曲线的影响

刘 勇，梁笑尘，汲胜昌，汪 伟，秦 睿，朱生鸿，孙 涛

（1.西安交通大学电力设备电气绝缘国家重点实验室，710049，西安；2.深圳供电局有限公司，518000，广东深圳；3.甘肃电力科学研究院，730050，兰州）

变压器是电力系统中关键且昂贵的设备之一，其可靠安全性对于保障整个电网的持续运行意义重大。当变压器遭到短路电流冲击时，绕组变形是其主要故障形式［1］。为了有效地对变压器绕组变形进行检测，人们开发了多种无损测试方法，其中频率响应分析法由于具有良好的测试重复性［2］和便携性［3］得到了普遍的应用。目前，利用频响法对变压器绕组变形进行检测时，考虑的影响因素主要是测试系统接地线与引线长度［4-7］、变压器油状态［8］和分接开关位置［4，6-7，8］等，但套管状态并未被过多考虑。据统计［9］，110kV及以上变压器由套管引发的事故占总事故台次的9.9%，如将变压器所发生的事故按损坏部位分类，套管所引发的事故居第2位，仅次于绕组［10］。随着电压等级的不断提高，套管事故所占比例也在不断上升，所以套管状态对变压器频响曲线的影响是一个不可忽视的问题。

文献［11-12］最早研究了高压套管对频响曲线的影响，发现扫频信号分别施加在套管顶端和末端时测得的频响曲线并不完全吻合，当频率小于3MHz时，二者基本相同；而当频率大于3MHz时，两者出现明显差异。文献［13］通过仿真得到套管电容性故障时，从套管顶端注入信号的频响曲线，与正常情况相比，在频率小于250kHz时两者基本重合，但在高频时套管电容性故障的频响曲线幅值较高。文献［14］提取了正常情况下单个套管的“离线”频响曲线与多个套管的“在线”频响曲线，经对比发现，“在线”测试时套管等效电容越大频响曲线的低频段越平滑，且在高频段时与“离线”频响曲线也越接近。综合看来，上述研究大多侧重于正常套管对频响曲线影响的探讨，虽然有部分学者考虑了套管故障，但只是进行了简单的仿真，并没有实测分析。实际上，对变压器进行频响法检测时，不论是“在线”还是“离线”都需要经套管把扫频信号加载到变压器绕组上，所以套管状态必然会在频响曲线中有所体现。因此，需要深入研究套管故障对变压器频响曲线的影响，为正确判定变压器绕组变形打下良好的基础。

1 试验对象及测试系统接线

1.1 试验对象

试验中被测变压器为特制试验变压器，如图1所示。为了便于更改绕组接线方式，三相高、低压绕组首末端皆装有套管，且固定于变压器外壳的顶端，其中A、B、C和X、Y、Z分别为三相高压侧绕组首端和末端套管，a、b、c和x、y、z分别为三相低压侧绕组首端和末端套管，其他套管定义以此类推。该变压器高、低压绕组有抽头引出，文献［15］指出，变压器绕组变形故障主要是绕组电感、纵向电容和对地电容发生变化所引起。因此，在抽头上进行短接、串并联电容和电感即可模拟各种类型的绕组变形故障。

图1 试验变压器实物图

图1 a中的3个变压器高压套管是为本文试验设计的电容式套管，可用于模拟多种套管故障。该套管有6层电容芯子，且每层电容芯子上都有导线引出，如图2所示。芯子间绝缘介质击穿是最为常见的一种套管电容性故障形式［16］，可通过短接芯子出线进行模拟。

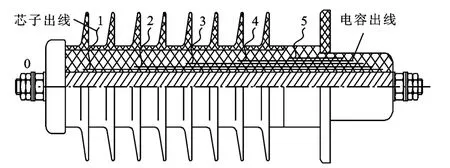
图2 变压器套管内部结构

1.2 测试系统接线

根据频率响应分析法的基本原理，在实验室中搭建的模拟测试系统，如图3所示，其中包括以下设备：扫频信号源、NF功率放大器、数据采集卡、计算机和试验变压器等。

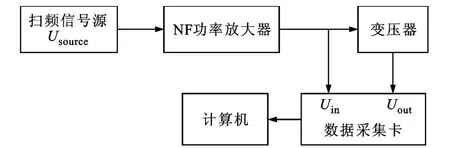
图3 测试系统示意图

由图3可知，测试时，首先扫频信号源发出幅值为5V、频率范围为1kHz～1MHz的激励信号，经过NF功率放大器后，幅值放大10倍，可大大提高测量的信噪比。然后该放大电压信号被用于两条支路，一条由数据采集卡端口Uin接收；另一条则进入变压器，其响应信号在绕组末端套管处被数据采集卡端口Uout接收。最后根据所采集的数据，得到不同频率下的传递函数H（jω），并画出频响曲线。通过对比不同时间段的频响曲线，可对变压器状态进行判定。数据处理公式为

变压器绕组变形频率响应分析法的电力标准［17］中指出：运用频率响应分析法检测变压器绕组变形，可采用两种激励源注入方式，一种为扫频信号通过套管末屏注入变压器绕组内部，简称末屏注入；另一种则是利用套管导杆注入扫频信号，简称导杆注入。因此，文中主要针对这两种测试方式下的频响曲线受套管容性故障影响的情况进行研究，其中导杆注入方式的等值电路如图4所示。

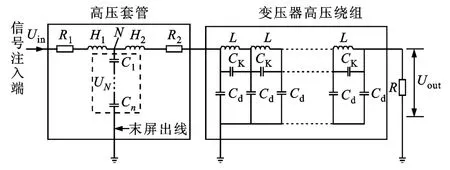
图4 变压器单相等值电路图

2 试验结果及分析

2.1 两种信号注入方式的频响曲线比较

在变压器正常情况下，分别采用套管导杆注入和末屏注入信号的方式得到变压器频响曲线，如图5所示。由图5可以看出，在频率为1～25kHz时，2条频响曲线的走势并不相同，导杆注入信号时，频响曲线的幅值随着频率的升高而降低。因为变压器绕组的感抗XL和频率f成正比，当频率f升高时，感抗XL变大，造成响应电压Uout降低，从而使得传递函数H（jω）也随之减小；而末屏注入信号时，其频响曲线与前者完全相反。这是由于电容式套管内部串联了多个屏间电容，在低频时，该电容处于高阻抗状态，使得H（jω）很小。随着频率的升高，容抗XC不断变小，从而造成H（jω）的增大。

星期六，我做完作业，想去找李立涵玩，可是他不在家。我又想去找周玉清，得知他和父母外出旅游。回到家后，我闷闷不乐地躺在沙发上，爸爸看见后，放下手机对我说:“儿子，我来给你表演个魔术吧！”

在频率为25kHz时，末屏注入方式下的频响曲线出现最大波峰，这是由套管电容和绕组电感产生串联谐振所造成的。此时，电路中的电压与电流相位相同，电路呈纯阻性，且总阻抗最小，总电流和匹配电阻R上的电压最大，因此频响曲线的幅值最高。同时，在相同频率的导杆注入方式下，频响曲线出现轻微波动，其原因是绕组的电感与匝间电容产生了串、并联谐振作用。

在频率为40kHz～60kHz时，2条频响曲线开始趋于相同，其幅值皆随频率的增大而减小，且当频率为60kHz时，两者都到达了最大的波谷，可知此时变压器集总参数发生了并联谐振。

当频率为60kHz～1MHz时，能明显看到2条频响曲线的走势和谐振点基本一致，但导杆注入方式下的频响曲线幅值要大于末屏注入方式的，且两条曲线的幅值差集中在7～12dB之间。其原因为在较高的频率下套管容抗较小，已不能对频响曲线产生较大影响，此时决定频响曲线走势和谐振点的主要为绕组状态。根据图4可知，末屏注入信号时，扫频电压注入位置由导杆首端变更为电容Cn的接地端，即套管末屏接地端。因此，套管电容与变压器绕组为串联关系，所以始终会有一部分电压加于套管电容，最终造成响应电压Uout小于导杆注入扫频信号的测试方式，反映在图5中即导杆注入方式下的频响曲线高于末屏注入方式的。

图5 两种信号注入方式的变压器A相正常频响曲线

2.2 套管电容性故障时频响曲线的测试分析

通过以上分析可知，采用末屏注入信号时，频响曲线易受套管状态的影响。下面，将采用末屏注入和导杆注入两种方式，对相同套管电容性故障进行测试，通过对频响曲线的分析，进一步验证该结论的正确性。其中，短路套管1-2号屏、1-3号屏、1-4号屏分别表示3种不同严重程度的电容性故障。根据图2可知，套管短路1-2号屏，即把套管1号和2号芯子出线相连，用于模拟1-2号电容屏击穿故障，其他短路依此类推。

（1）导杆注入信号。当短路套管分别处于1-2号屏、1-3号屏、1-4号屏时，测试得到的频响曲线与套管正常时对比，如图6所示。

图6 导杆注入时A相套管电容性故障与正常情况的对比

从图6可以看出，图中的4条频响曲线基本重合。利用图4能够很好地解释上述现象。已知套管等效电容为

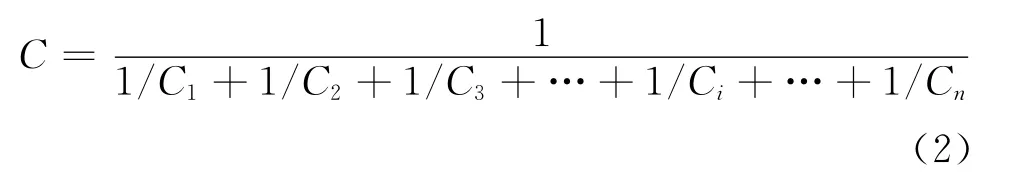
式中：C为等效电容；Ci为第i个串联的屏间电容，i=1～n。当串联电容的个数减少，即n变小时，等效电容C增大，套管容抗XC变小，又由于图上节点N之前还串联有导杆电阻R1和电感H1，所以电压UN减小。考虑到套管电容与由导杆电阻R2、电感H2、变压器高压绕组和匹配电阻R组成的支路相并联，所以匹配电阻R上电压Uout也随之减小，由式（1）可知最终传递函数H（jω）也会变小。由于导杆电阻R1、R2和电感H1、H2都极小，其影响可忽略不计，所以故障曲线与正常曲线基本重合。

为了更加直观地了解套管故障对频响曲线的影响，根据文献［17］，可得3条套管故障频响曲线与正常情况的相关系数（低频相关系数RLF，中频相关系数RMF，高频相关系数RHF）及具体判据，如表1所示。

由表1可知，当通过导杆注入信号时，3条故障曲线与正常情况的相似度极高，并不会影响绕组变形的判定，且随着频率升高，相关系数减小，该结果与上文分析相符。综上所述，当利用导杆注入信号时，套管电容性故障不会对频响曲线产生影响。

表1 导杆注入A相出现套管故障的相关系数

（2）末屏注入信号。本节采用末屏注入的方式，对各电容屏故障时变压器绕组的频响曲线进行测试，并与正常情况进行对比，如图7所示。

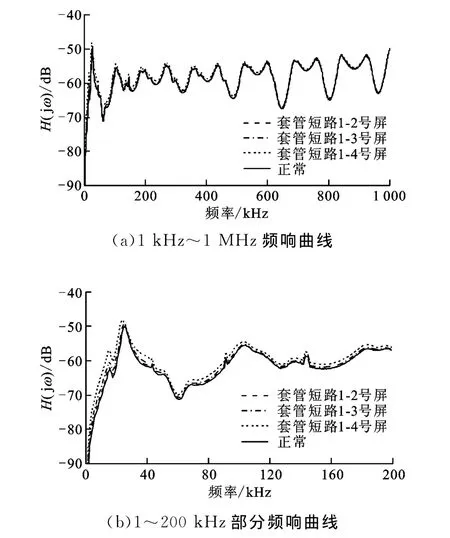
图7 末屏注入时A相套管电容性故障与正常情况的对比

由图7可以看出，在整个频段中，4条频响曲线的走势基本相同，但幅值却有明显差异。在频率为1～25kHz时，4条曲线的幅值高低是由短路电容屏的个数所决定的，短路个数越多则幅值越高。低频时，套管的容抗XC较大，绕组的感抗XL较小，所以套管状态决定了频响曲线的走势。如果此时套管等效电容发生改变，则会造成频响曲线的变化，具体原因分析如下。

由式（2）可知，当串联电容的个数n减少时，套管等效电容变大，容抗XC变小。此外，由于图4中的套管电容、变压器绕组和匹配电阻R为串联关系，所以容抗XC越小，匹配电阻R上的电压越高，传递函数H（jω）越大。由此可知，该频段频响曲线的幅值高低与套管等效电容的大小为正相关。

从图7中还可看出，大约在25kHz时，4条频响曲线都出现了最大波峰，原因与图5相同，但4个波峰所对应的频率却略有不同，由低到高依次为套管短路1-4号屏、1-3号屏、1-2号屏和正常情况。具体原因为：绕组电感L不变，套管电容C增大，则谐振频率f降低。因此，图7中波峰所对应的频率会随套管等效电容的增大而降低。

当频率为25kHz～1MHz时，随着频率的升高，3条故障曲线在逐渐接近正常曲线。由于频率升高，电容容抗XC减小，套管电容对响应电压Uout的影响变小；与此相反，绕组电感的影响则增大。当套管发生电容性故障时，绕组电感不变，因此4条频响曲线会在高频处趋于重合。根据测试曲线，得到图中3条套管故障频响曲线与正常情况的相关系数，如表2所示。

表2 末屏注入时A相出现套管故障的相关系数

从表2可知，随着频率的升高，3条套管故障频响曲线与正常情况的相关系数变大，这进一步说明了在套管末屏注入时，套管电容性故障主要影响频响曲线的低频段。当套管短路1-3号屏时，其频响曲线低频段的相关系数已接近绕组轻度变形的范围，而套管短路1-4号屏时，绕组状态则会被判定为轻度变形［17］。

为了验证以上分析结果的正确性，本文另外测量了B、C相套管出现与A相相同的电容性故障时的变压器频响曲线，并与正常情况进行了对比，如图8和图9所示。从中可以看出，频响曲线的变化趋势与图7基本相同，由此再次证实了以上对套管电容击穿时频响曲线变化原因的分析。计算得到B、C相出现套管故障时的相关系数如表3所示。从中可以看到，B、C相在套管短路1-4号屏时，由相关系数的值进行诊断，同样会得出绕组发生变形的结果。结合表2的判定结果可知，采用末屏注入时，如套管电容性故障比较严重，将会误判为绕组变形故障。

采用导杆注入信号时，套管电容性故障并不会对频响曲线产生影响，也不会影响相关系数对绕组变形故障的判定；但由末屏注入信号时，套管电容性故障会对变压器频响曲线产生较大影响，具体表现为变压器频响曲线全频段幅值升高，且在低频段时幅值升高最为明显。同时，由相关系数分析得出：当由末屏注入信号时，套管电容性故障会对绕组状况的诊断产生影响，严重时会引起误判。

图8 B相套管电容性故障与正常情况频响曲线的对比

图9 C相套管电容性故障与正常情况频响曲线的对比

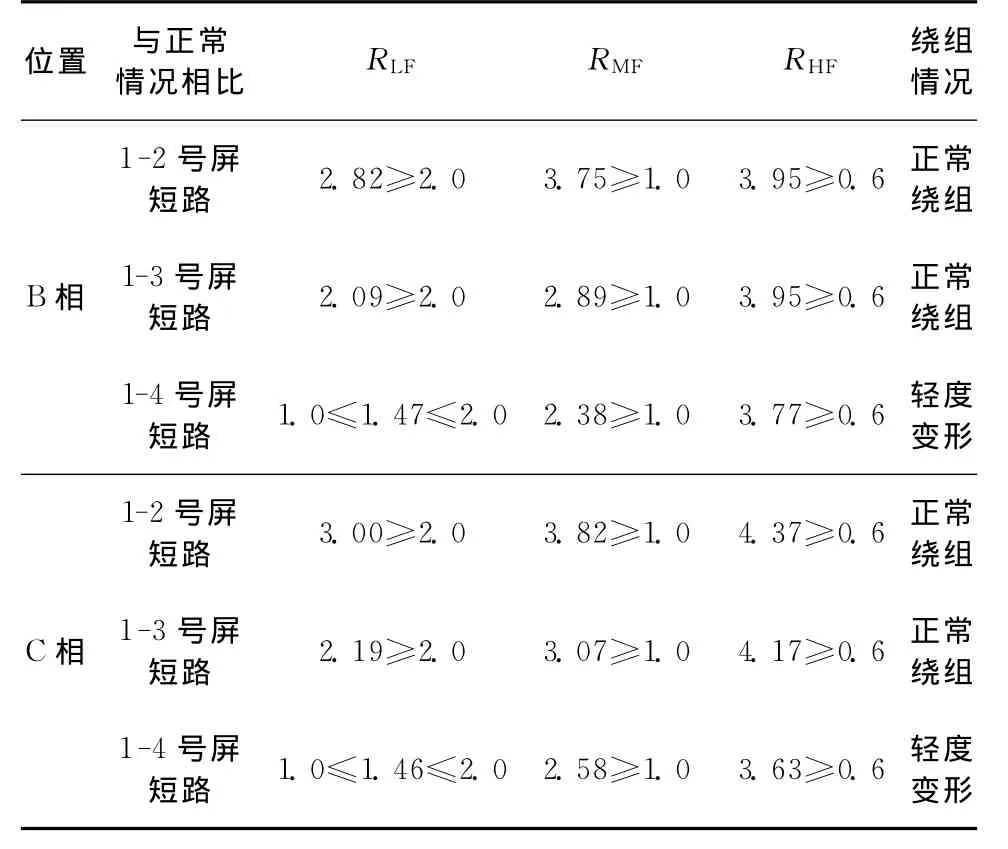
表3 末屏注入时B、C相出现套管故障的相关系数

2.3 套管电容性故障与绕组故障的比较

本文套管电容性故障为套管短路0-4号屏，绕组电感故障为A相高压绕组短路1-2号屏，绕组纵向电容故障为A相高压绕组1-2号屏之间并联470pF的电容，而绕组对地电容故障则为A相高压绕组第5号屏与地之间并联47pF的电容。利用末屏注入方式得到以上4种故障形式的频响曲线，并与正常情况频响曲线进行了比较，如图10所示。

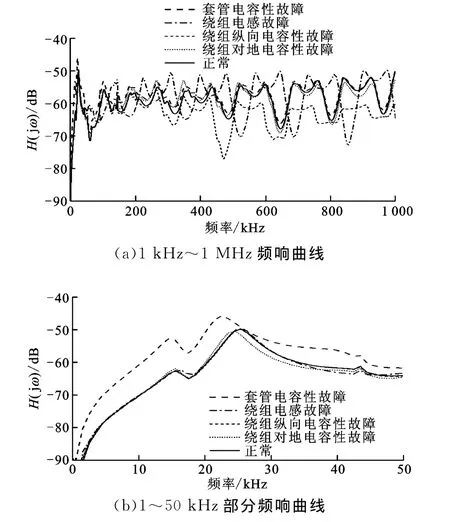
图10 A相套管电容性故障与绕组变形故障的频响曲线对比

由图10可以看出，在频率为1～50kHz时，除了套管电容性故障以外，其他3种绕组变形故障的频响曲线与正常情况基本重合，而套管故障时的频响曲线幅值则较高，在1～25kHz时该情况尤为明显。此现象再次证明了低频时频响曲线受套管状态影响较大的特点。当频率为50kHz～1MHz时，4条故障频响曲线与正常情况相比则完全不同：套管电容性故障主要表现为频响曲线幅值增大，其走势与正常情况相同；绕组电感故障则表现为频响曲线的波峰、波谷向高频处移动，且波谷幅值减小，波峰幅值增大；绕组纵向电容故障表现为频响曲线幅值明显降低，谐振点向低频处移动，当频率大于500kHz时，波峰、波谷趋于消失；绕组对地电容故障为频响曲线幅值减小，其走势与正常情况相同。

综上所述，在末屏注入信号时，套管电容性故障的频响曲线并不同于绕组变形故障，具有很强的可辨识性，且低频段频响曲线主要受套管状态的影响，而中、高频段的频响曲线则主要由绕组状态所决定。由此可知，套管的特征变量位于1～25kHz，即频响曲线的最大波峰之前，如发生套管电容性故障，该频段的频响曲线会出现幅值的升高。当然，对于不同电压等级的变压器而言，由于套管及绕组等值分布电路模型的参数略有不同，套管电容性故障的特征频段会与本文的被试变压器有所差别，但从原理上来说都会集中在扫频曲线的低频段。

3 结 论

（1）利用套管导杆注入信号时，套管电容性故障的频响曲线与正常情况基本重合，且利用相关系数作为判据，并不会对绕组变形故障产生误判。所以，当激励源位置为导杆时，套管电容性故障并不会对频响曲线产生影响。

（2）采用套管末屏注入信号时，套管电容性故障的频响曲线与正常情况相比会出现幅值上升和谐振点频率降低的现象，且故障越严重，其频响曲线的幅值越高，谐振点频率越低。对于文中所试变压器而言，在频率为1～25kHz时，即最大波峰所对应的频率之前，这种变化最为明显。采用相关系数诊断绕组状态时，套管电容性故障越严重，对相关系数的影响越大，从而容易误判为绕组变形故障。

（3）利用末屏注入方法，通过4种故障形式（套管电容性故障、绕组电感故障、绕组纵向电容故障和绕组对地电容故障）频响曲线与正常情况的比较，验证了套管发生电容性故障时的频响曲线具有可辨识性，并确认了套管状态的影响范围主要表现在变压器频响曲线的低频段。

从本文的研究来看，根据相关系数判断绕组状况的判据对于末屏注入方法而言并不完善，而套管故障时在频响曲线上的表现又具有可辨识性，因此应继续深入开展由频响曲线分别诊断变压器绕组和套管各自状况的方法，从而避免误判，提高诊断的可靠性和可信度。此外，在线测试大多利用套管电容耦合的方法将扫频信号加于变压器绕组中，所以文中的研究对在线监测变压器绕组变形也具有一定的参考价值。

［1］ 凌愍，王圣.110kV级变压器事故统计及短路故障分析 ［J］.变压器，1995（12）：33-36.

［2］ DICK E P，ERVEN C C.Transformer diagnostic testing by frequency response analysis［J］.IEEE Transactions on Power Apparatus and Systems，1978，97（6）：2144-2153.

［3］ 王钰，李彦明，张成良.变压器绕组变形检测的LVI法和FRA法的比较研究 ［J］.高电压技术，1997，23（1）：13-15.

WANG Yu，LI Yanming，ZHANG Chengliang.The comparisonal study on LVI and FRA method of detecting winding deformation faults in transformers ［J］.High Voltage Engineering，1997，23（1）：13-15.

［4］ 姚森敬，欧阳旭东，林春耀.电力变压器绕组变形诊断分析 ［J］.电力系统自动化，2005，29（18）：95-98.

YAO Senjing，OUYANG Xudong，Lin Chunyao.Analysis on winding deformation diagnosing of power transformers［J］.Automation of Electric Power Systems，2005，29（18）：95-98.

［5］ RYDER S A.Diagnosing transformer faults using frequency response analysis［J］.IEEE Electrical Insulation Magazine，2003，19（2）：16-22.

［6］ 戴文进，刘保彬.用频率响应法检测变压器绕组的变形 ［J］.高压电器，2004，40（6）：464-465.

DAI Wenjin，LIU Baobin.Monitoring the distortion of transformer winding using frequency response method［J］.High Voltage Apparatus，2004，40（6）：464-465.

［7］ 吴国跃，李世伟，刘多禄.电力变压器绕组变形实测中的影响因素 ［J］.高电压技术，2001，27（3）：81-82.

WU Guoyue，LI Shiwei，LIU Duolu.Analysis of influence factors in detecting power transformer winding deformation［J］.High Voltage Engineering，2001，27（3）：81-82.

［8］ 何文林，陈金法，应高亮，等.频响分析法测试变压器绕组变形的研究 ［J］.中国电力，2000，33（12）：42-45.

HE Wenlin，CHEN Jinfa，YING Gaoliang，et al.A study on detecting winding deformation in transformers with FRA method［J］.Electric Power，2000，33（12）：39-42.

［9］ 王梦云，薛辰东.1995～1999年全国变压器类设备事故统计与分析 ［J］.电力设备，2001，2（1）：11-19.

WANG Mengyun，XUE Chendong.Nation-wide statistics and analysis on power transformers faults in 1995～1999［J］.Electrical Equipment，2001，2（1）：11-19.

［10］张淑珍，傅锡年，朱建新.500kV变压器、电抗器的套管事故及障碍分析 ［J］.电力设备，2002，3（4）：7-11.

［11］WANG M，VANDERMAAR A J，SRIVASTAVA K D.Transformer winding movement monitoring in service-key factors affecting FRA measurements［J］.IEEE Electrical Insulation Magazine，2004，20（5）：5-12.

［12］WANG M，VANDERMAAR A J，SRIVASTAVA K D.Improved detection of power transformer winding movement by extending the FRA high frequency range［J］.IEEE Transactions on Power Delivery，2005，20（3）：1930-1938.

［13］HASHEMNIA N，ABU-SIADA A，MASOUM M A S，et al.Characterization of transformer FRA signature under various winding faults［C］∥Proceedings of 2012IEEE International Conference on Condition Monitoring and Diagnosis.Piscataway，USA：IEEE，2012：446-449.

［14］BAGHERI M，NADERI M S，BLACKBURN T，et al.Bushing characteristic impacts on on-line frequency response analysis of transformer winding ［C］∥2012 IEEE International Conference on Power and Energy.Piscataway，USA：IEEE，2012：956-961.

［15］ISLAM S M.Detection of shorted turns and winding movements in large power transformers using frequency response analysis［C］∥Power Engineering Society Winter Meeting.Piscataway USA：IEEE，2000：2233-2238.

［16］王世阁.变压器套管故障状况及其分析 ［J］.变压器，2002，39（7）：35-40.

WANG Shige.Fault situation of transformer bushing and its analysis［J］.Transformer，2002，39（7）：35-40.

［17］中国电力企业联合会.电力变压器绕组变形的频率响应分析法 DL／T 911-2004［S／OL］.［2013-08-10］.http：∥www.bzko.com／std／28209.html.