基于APM模型的电磁波三维可视化研究与实现＊

王春雨 田 斌 冯 超

（1.海军工程大学电子工程学院海洋电磁环境研究所 武汉 430033）（2.武汉军械士官学校 武汉 430075）

1 引言

随着部队信息化进程的加速建设，各种武器装备都已经主动或者被动地处于复杂的电磁环境中，电磁环境研究成为了当前军事领域研究的一个热点和重大课题[1]。可视化技术作为一种用于知识发现与理解的工具成为电磁环境最重要表现手段和核心技术，电磁环境可视化，可使人们方便地查阅作战区域内的电磁场分布情况，形象直观地获得所需要的战场电磁信息，反映全局的电磁分布特征，准确把握战场电磁态势。但目前国内在这方面多是具体针对雷达探测范围进行可视化研究，需要假定一定的目标参数，不是真正意义上的电磁环境可视化，表现在二维坐标中就是常见的雷达威力图，在三维中是对探测范围面的三维显示，如文献[2～4]中对复杂电磁环境可视化的研究。因此，探索一种能全空域反映电磁环境的方法是一个亟需要解决的问题。

2 电磁场可视化的研究

2.1 电磁环境的特点

在某一特定空间范围内存在的所有无线电波在频率、功率和时间上的分布称为电磁环境，可用电磁场强分布表示。其主要特点是：1）空间范围广阔；2）时间随机分布；3）频率拥挤重叠；4）能量分布不均；5）信号密度高。正是这些复杂特点导致了可视化的效果一直不理想。

2.2 常见的三维可视化方法

1）颜色法

可视化系统中，常用颜色表示数据中的数据大小，即在数据与颜色之间建立一种映射关系，把不同的数据映射为不同的颜色。如果对于精度要求不是很高的时候也可以将某个数值范围内的数据块映射为同一种颜色，这样可以减少计算量，提高绘制效率，在文献[5]中也称为分色云图法。在绘制图形时，根据数据场中的数据确定点或图元的颜色，从而以颜色来反映数据场中的数据及其变化规律。

2）等值面

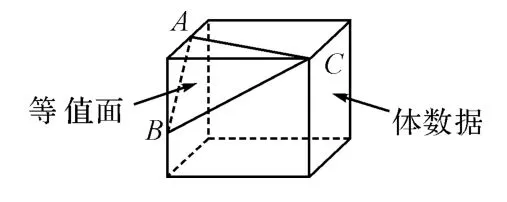
图1 MC方法的示意图

为了清楚地表现重点观察数值的分布情况，常常采用等值面技术，其中Marching Cube（MC）算法是三维数据场等值面生成的经典算法，是体素单元内等值面抽取技术的代表。算法的核心思想是处理数据场中每一个的立方体，分类出与等值面相交的立方体，采用插值计算出等值面与立方体边的交点。根据立方体每一顶点与等值面的相对位置，得到将等值面与立方体边的交点，然后按一定的方式连接生成等值面（如图1所示），作为等值面在该立方体内的一个逼近表示。

3）体绘制

由于我们使用的显示设备绝大多数都是二维的平面显示器，为了在二维平面上显示出逼真的三维绘制效果，体绘制算法是一个不错的方法。它可以分为以图像空间为序、物体空间为序和混合空间为序算法，以图像空间为例，它是从屏幕上的每一象素点出发，根据视点方向，发出一条射线，这条射线穿过三维数据场，沿射线进行等距采样，求出该采样点的不透明度值及颜色值，将每一个采样点的颜色及不透明度进行组合，从而计算出屏幕上该像素点处的颜色值。

3 APM模型简介

APM模型是在PE（抛物方程模型）的基础上综合几种其他的电磁波传播模型发展而来的一种混合模型，该模型的特点是将传播区域划分为四个部分：平坦地面（Flat Earth，FE）、射线光学（Ray Optics，RO）、抛物方程（Parabolic Equation，PE）和扩展光学（Extended Optics，EO），如图2所示。APM模型和PE模型相比不仅没有降低计算的精度，反而增加了计算速度。

此模型被应用到了美国海军新发展的新型传播预报系统—高级折射效应预报系统（AREPS）中。该系统不仅可以用于海上还可用于陆地等复杂的地理环境条件中，在输入环境数据和辐射源的信息后，可以计算出高准确度的雷达探测、通信系统和电子支援数据，并可以把数据保存下来。

图2 APM模型区域划分

4 利用Matlab对电磁波的可视化仿真

4.1 数据的获取

设置初始条件后，通过APM模型计算出垂直剖面离散电磁数据，保存下来。初始环境设定如表1所示。

表1 初始条件的设置

利用Matlab读取文件函数fopen、fscanf和textread等，将需要的数据提取到变量中，方便下一步使用。

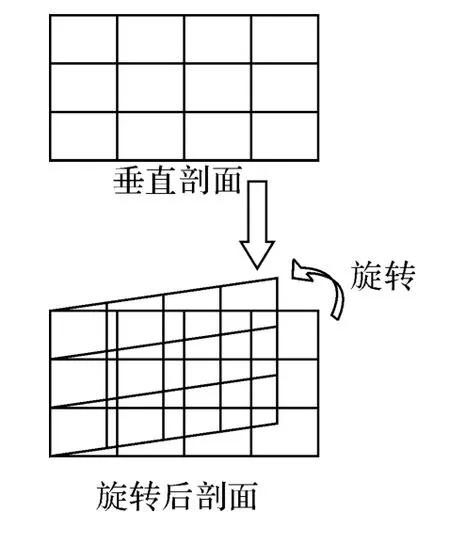
图3 旋转变为三维数据的示意图

4.2 数据从二维到三维的变换

由于APM模型计算的是一个垂直二维剖面上的数据，不能全空域地反映电磁波的强度，因此需要对其进行三维变换。易知发射源是向四周发射电磁波的，因此最好的三位转换方法就是将剖面沿着过发射源且垂直于地面的直线做等角度圆周旋转，等价于在圆周上做采样，那么旋转的角度就决定了电磁场数据在圆周切线上的精确度，如图3所示。这样就得到了三维的电磁场立体数据。

4.3 颜色的分配

在Matlab画立体图时，颜色是用一个参量表示的[6]，因此本文将每一点处的电磁场强度值映射为该点处的颜色值，那么不同的颜色就可以表示为不同的场强值，颜色相同的地方就表示场强值一样，典型的几种颜色表如表2所示。

表2 Matlab的几种颜色方案

4.4 等值面的提取

由于本文中的三维数据是由二维剖面数据旋转得到的，因此形成的电磁数据格式表现在柱坐标中是规则数据，但是在笛卡尔直角坐标系中却是杂乱的，并且Matlab中关于求等值面的函数如isosurface和patch等都是应用在直角坐标系且利用meshgrid产生的规则数据体中的，因此不能直接调用函数进行绘图[7]。

对于这个问题有两种解决方法：

1）在直角坐标系中把不规则的数据通过插值、重新划分网格点，得到新网格上每一点的数据，以此来规整数据。但是这种方法存在两个缺点：一是通过插值产生的数据会积累误差，使准确度变低。二是由于全体数据为柱状数据体，所以在整个绘制范围的边界部分即立方体的边缘位置插值的数据会产生畸变，严重影响最后结果。

2）通过了解计算机画图的原理和画图过程发现Matlab在绘制等值面时，先把符合等值条件的点和面一一找出来，然后把这些点按照一定的规则连接起来得到等值面，这两个步骤分别是由两个参数控制的（在isosurface函数中为F，V）。由此我们可以在柱坐标中利用规则的数据找到等值的点和连接的规则，然后再把这些点转化到直角坐标中。这种方法不仅能保持数据的原始性，而且实现过程也相比第一种方法简单、易操作。

整个过程的流程图如图4所示，最后再加上光照和透明度等效果，效果图如图5所示，从图中可以看出该立体图形不精可以显示一个等值面而且可以表现整个空间内部的电磁场信息，且颜色由中心向四周渐变对应于颜色条上的蓝色向红色端过渡，越红表示电磁波的衰减越来越大，场强越来越小，与实际情况相符合，同时比以往仅仅只有探测范围的三维可视化更加全面、清晰。

图4 流程图

图5 最终效果图

5 结语

电磁环境可视化对于未来信息化作战是不可或缺的技术之一，但由于电磁环境的数据量大、维数多等特点，导致目前可视化的研究还存在很多问题。本文在用APM模型产生数据的基础上，巧妙地对数据进行了三维拓展，而且在等值面抽取时尽可能地减小了误差。最后利用Matlab强大的图形处理功能较好地实现了整个立体数据场的可视化，并且得到重点场值的等值面，在电磁环境可视化方面做了积极的探索和尝试。

[1]高光英，高永明，董正宏.空间复杂电磁环境快速可视化研究[J].现代电子技术，2012（10）：132－133.

[2]张敬卓，袁修久，赵学军，等.基于APM的雷达探测范围三维可视化[J].计算机工程，2012：281－283.

[3]袁新恩.复杂电磁环境仿真中态势可视化技术研究[D].南京：南京理工大学，2011：35－46.

[4]董凯，李伟明，姜本清，等.数字化战场中雷达探测区域可视化技术研究[C]／／第13届中国系统仿真技术及其应用学术年会论文集，2011.

[5]姚丽娇.科学计算中的标量场可视化技术[D].沈阳：东北大学信息科学与工程学院，2009：19，34.

[6]张航，黄攀.精通Matlab 6[M].北京：清华大学出版社，2002：344－356.

[7]刘正君.MATLAB科学计算与可视化仿真[M].北京：电子工业出版社，2009，4.