不同布局下高超声速飞行器FADS求解精度①
陈 康,符文星,闫 杰
(西北工业大学 航天学院,西安 710072)
0 引言
嵌入式大气数据传感(Flush Airdate Sensing,FADS)系统是一种依靠嵌入飞行器前端的压力传感器阵列来测量飞行器表面的压力分布,并由此压力分布间接获得飞行参数的飞行数据传感系统。与传统的基于空速管的大气数据传感系统相比,FADS系统在精度、可靠性、适应范围上都具有更大的优势[1]。
采用FADS系统求解大气参数,关键步骤是获取精确的压力分布。对于不同的飞行器外形,其测压点数目和布局相对固定[2]。例如,F-18HARV采用了23个测压孔,23个压力传感器,其中11个传感器处于系统的正常工作状态,其余12个作为系统的备份;X-31采用6个压力传感器,其中5个处于正常工作状态,第6个作为系统的备份。对于FADS系统而言,多传感器的信息融合需要特定算法,在算法的基础上,通过传感器的精确数据和计算机的高速处理,从而获得攻角、侧滑角等大气数据。由于FADS系统优良的性能和广阔的适用范围,所以备受各国航空航天领域工程技术人员关注,目前的研究主要集中在测压孔位置及数量优化技术、CFD仿真技术、数据融合技术、高精度压力传感器等方面。
本文基于X-33高超声速飞行器的结构外形,利用计算流体力学方法求解飞行器前端的压力分布,采用三点法求解攻角和侧滑角,并对求解数据进行修正;然后,变换测压点布局,采用相同方法进行数据处理;最后,对不同布局下的结果进行对比和分析,以得到在不同布局下高超声速飞行器FADS系统的解算精度。
1 FADS系统的计算机仿真模型
X-33为降低系统噪声敏感度和提高冗余度,采用6个独立的测压点来计算大气参数[3]。本文采用X-33前端1/10比例模型,基于仿真中无干扰和降低计算量的考虑,选取不同布局下的5点分别进行攻角和侧滑角的求解。鉴于在某一状态下3号点测得的压力一定,亦可单独选取纵向3点求解攻角;然后,选取横向3点求取侧滑角,其测压点分布见图1,CFD软件中建立的仿真模型及坐标见图2。
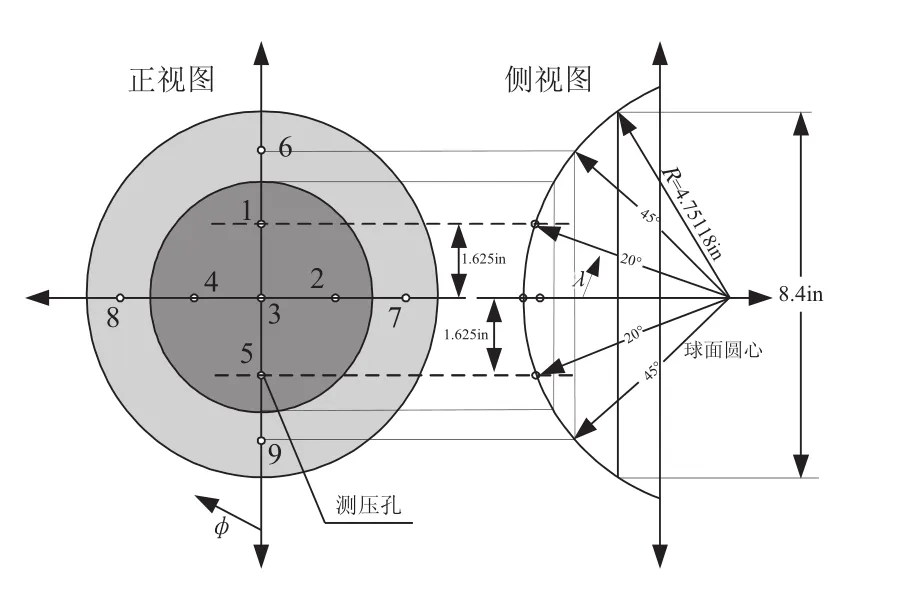
图1 测压点分布Fig.1 Layout of the pressure points

图2 Ansys1 2.0中建立的头部模型Fig.2 Head model in Ansys1 2.0
图1中,λ为测压点的圆锥角,是测压点表面法线方向与球顶纵轴之间额夹角;φ为测压点圆周角,是由机身底部为起点顺时针到该测压点转过的角度。坐标角描述见图3。
在仿真模型中,定义的测压点圆锥角、圆周角对应的角度值见表1。
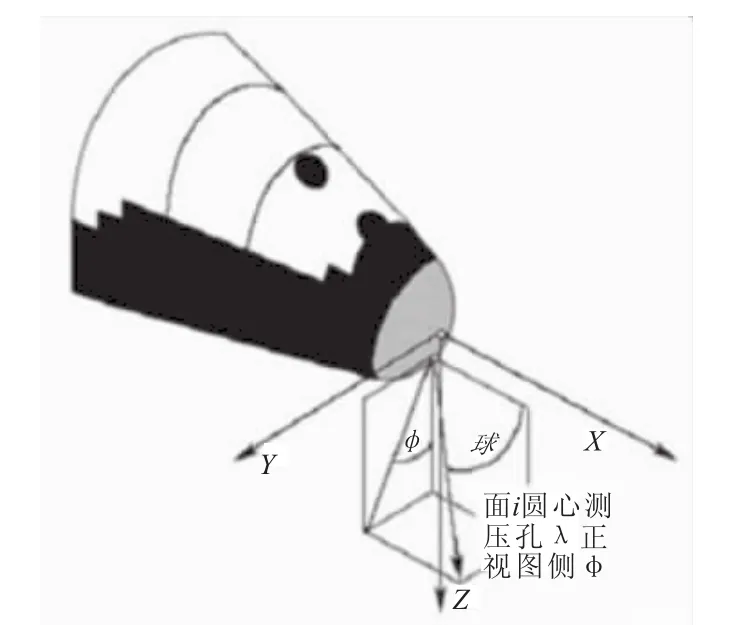
图3 圆锥角、圆周角的定义示意图Fig.3 Sketch of conical angle and circumferential angle

表1 各测压点圆锥角λ、圆周角φ角度值Table 1 Values of conical angle λ and circumferential angle φ at each pressure point
在低马赫数下,将钝头体的FADS系统模型视为适合次音速的potential flow模型[4]。在CFD仿真中,只能分别求得各测压点的静压和动压,而动压方向与来流方向相同,通过将仿真中测得的各点动压折合为垂直于该点切线方向的分量后,再与该点处静压作和,就可得到用来替代FADS系统压力传感器实测量的压力值。在有攻角和侧滑角的情况下,压力折合运算公式为
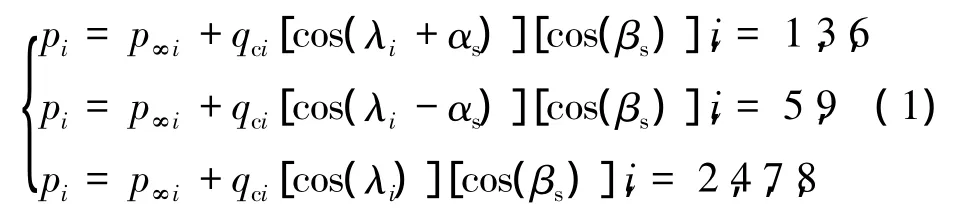
式中 pi为i号测压点压力,Pa;p∞i为仿真计算中i号测压点处静压,Pa;qci为仿真计算中i号测压点处动压,Pa;λi为i号测压点的圆锥角,rad;αs为仿真过程中设定的攻角,rad;βs为仿真过程中设定的侧滑角,rad。
2 攻角、侧滑角的求解
利用Ansys1 2.0进行仿真计算,得到每一点处的静压和动压后,依据式(1)可获得在特定状态(飞行马赫数和飞行攻角)下的每一点的压力;然后,依据三点法[5]对攻角和侧滑角进行求解。
对于攻角,定义:
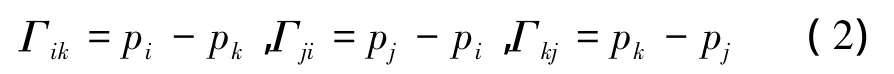
其中,pi、pj、pk为测压点压力;i,j,k 为下标,代表测压点序号,此时 i、j、k=1、3、5 或 6、3、9,且 i、j、k 互不相等。
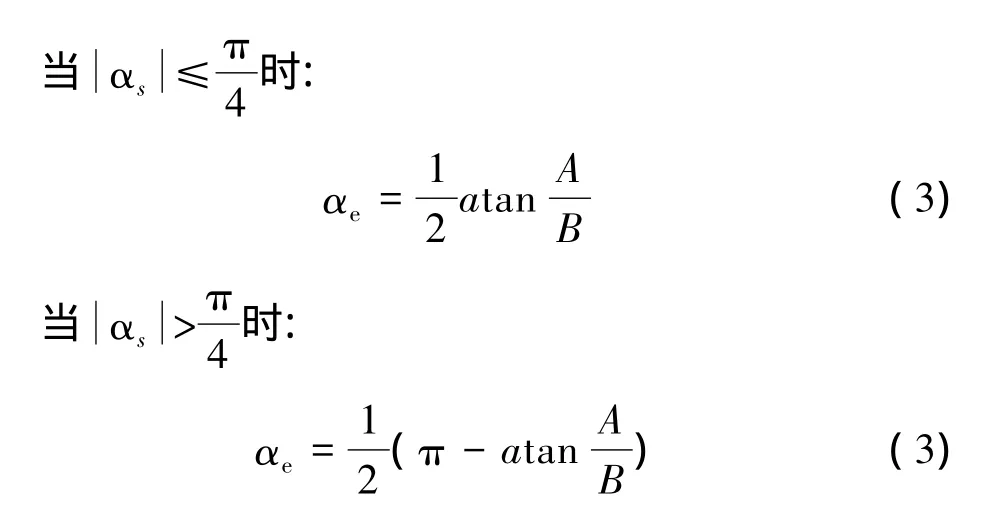
其中,αs为仿真过程中设定的攻角;αe为初步计算攻角。

求出初步计算攻角后,对于侧滑角,定义:
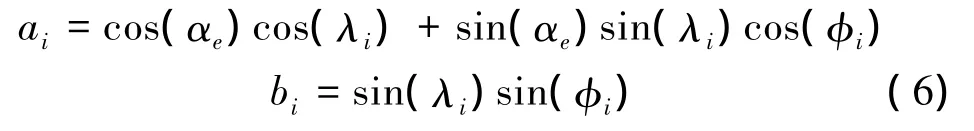
则
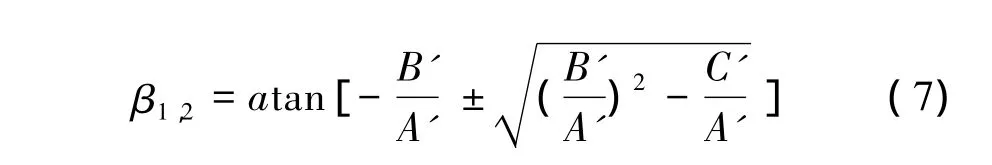
初步计算侧滑角βe,选取较小的值。
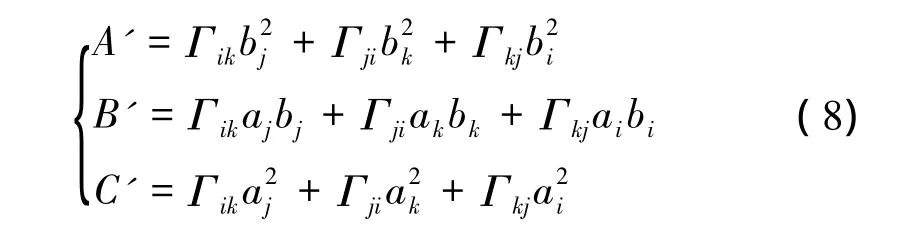
3 仿真结果及分析
3.1 仿真结果
利用Ansys1 2.0对所建模型进行压力迭代计算,采用隐式方程,非动态网格,网格数为120万,设置迭代次数为2 500次以上,压力分布仿真结果见图4。从图4来看,当头部无攻角时,压力分布均匀,以球型头部中心为最大压力点,压力向外扩散,呈逐渐减小趋势;当头部有攻角时,最大压力点移动,攻角为正时向下移动,移动角度大小与攻角大小有关,攻角越大,移动角度越大。另外,距离最大压力点越近的点,压力衰减越快。
设定所建模型在海平面以上20 km处巡航飞行,在此高度时,压强为5 745 Pa,通过设定边界条件,可获得在不同飞行状态下的压力分布;然后,根据三点法可求得初步计算结果。其中,部分仿真数据和初步计算数据见表 2。以 1、2、3、4、5 点构成布局一,以 3、6、7、8、9 点构成布局二,以 1、2、3、4、6 点构成布局三。

图4 模型表面压力分布正视图和侧视图Fig.4 Front view and side view of surface pressure distribution
3.2 数据校正
从表2可见,初步计算攻角与仿真设定攻角之间有一定偏差。本文采用曲线拟合的方法[3],对初步计算结果进行修正,令初步计算攻角的修正量为

对各状态下的修正量,采用三次多项式:

进行拟合求解校正曲线。则最终计算结果αc为

侧滑角的校正与攻角的校正类似,此处不再赘述。
在获得初步计算攻角和侧滑角后,根据修正公式(9)、(10),应用Matlab工具,采用最小二乘法对各状态下的初步计算结果与相应偏差量进行三次多项式拟合校正。不同测压点布局下拟合结果见图5。

表2 部分仿真数据和初步计算数据Table 2 Partial simulation data and primary calculation data under the first arrangement

图5 攻角校正曲线Fig.5 Calibration curve of the attack angle
从图5可看出,不同布局下的拟合曲线差异较大;在固定马赫数下,均采用6个状态点求解拟合曲线,在布局一下,计算数据分布均匀且初步计算攻角就在设定攻角附近2°范围,但曲线曲率较大,在曲率突变处容易造成修正后的攻角误差超出允许范围;在布局二下,拟合曲线显得相对平滑,但仍存在曲率正负变化问题,且计算结果分布不均匀,需对初步计算结果进行较大幅度的修正;在布局三下,拟合曲线曲率最为平滑,修正后的结果与设定结果最为吻合,计算结果分布较为均匀,但仍需对初步计算结果进行较大幅度的修正。依据拟合曲线对计算数据进行校正,其中部分结果见表3。
为验证校正结果是否准确,选择曲线拟合过程中未采用的各马赫数下2°、6°值,用拟合曲线对各状态下初步计算结果进行校正,结果见表4。
从拟合结果来看,由于在求解拟合曲线时并未采用在2°、6°下的计算值,拟合校正后结果与设定结果偏差要比其他角度下的结果稍大一些。布局一下的修正结果偏差最大,部分数据误差超出0.5°;布局二下数据整体偏差稳定,修正后结果与设定结果偏差约0.3°左右;由于布局三的拟合曲线曲率变化平滑,修正后的结果大部分精度较高,仍能保证在0.1°左右,但部分结果出现较大的误差,达0.3°以上,难以判断最终结果的准确度。综上,布局二下由于采用对称性布局且测压点分布较远,结果较为稳定且修正后的数据精度也较高,基本保证在 0.3°。
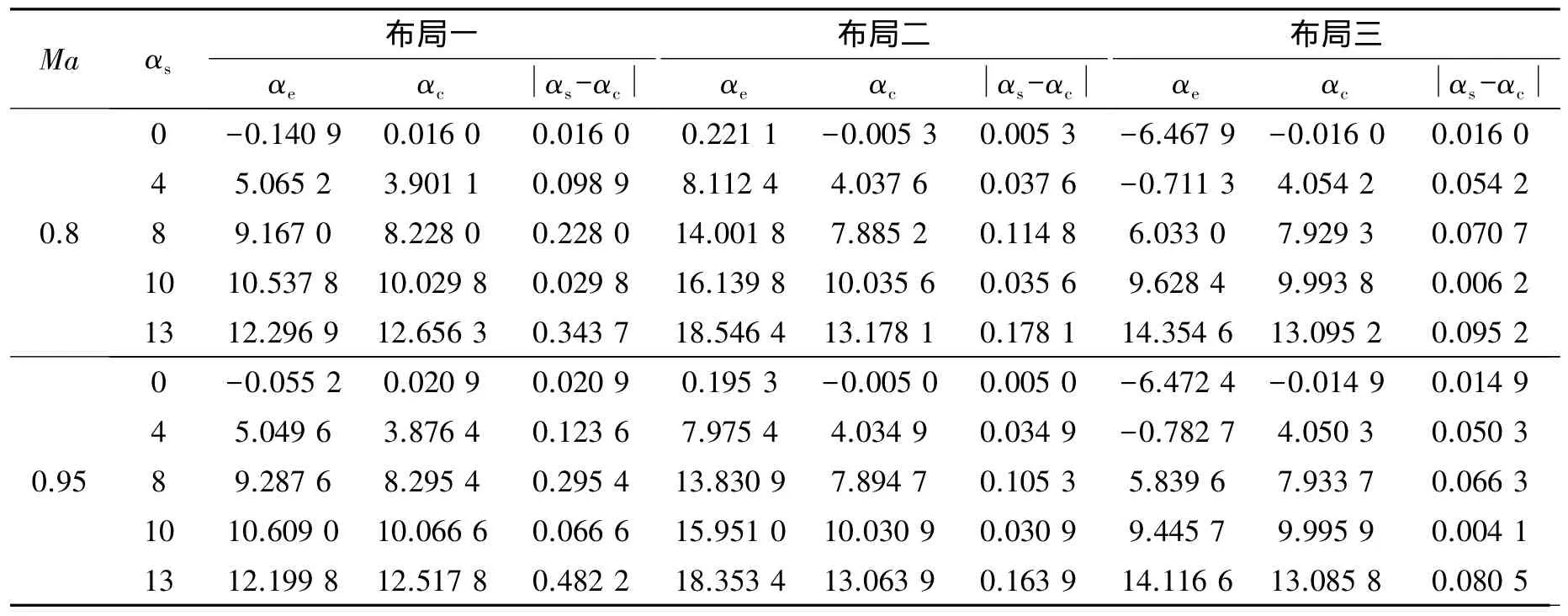
表3 不同状态的部分攻角校正结果Table 3 Partial calibration results of the attack angle in different conditions (°)
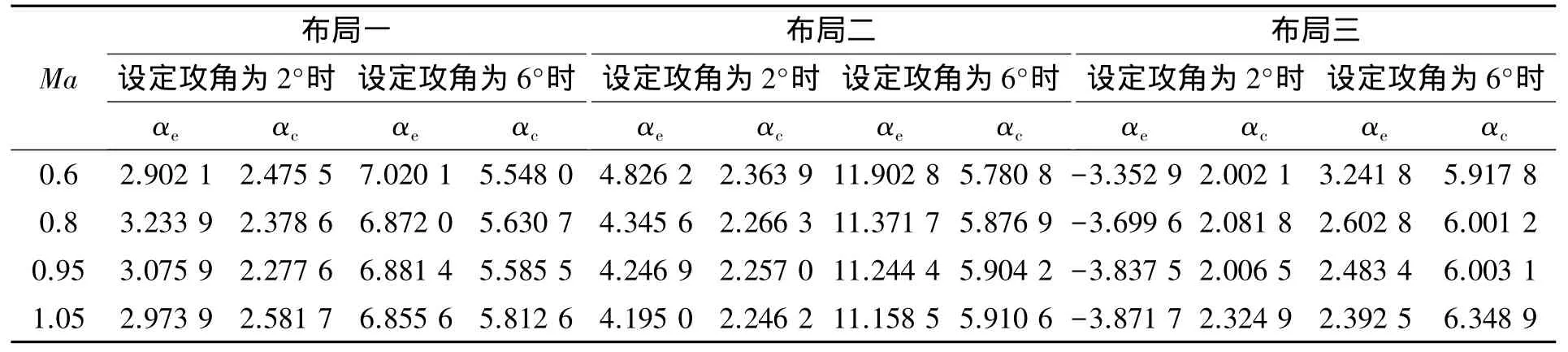
表4 另选角度下的攻角校正结果Table 4 Calibration results of the attack angle in different degrees (°)
4 结论
(1)在低马赫数下,利用计算机仿真的FADS系统的求解具有较高精度,基于布局二的攻角求解误差基本控制在 0.3°。
(2)测压孔对称性布局适用于钝头体,且测压孔分布较远的布局比测压孔分布较近的布局在求解精度上具有优势。
(3)非对称布局情况下,在求解攻角时出现修正数据与设定数据偏差不稳定现象,不利于判断最终数据的准确性。
[1] 邵笑杰.嵌入式大气数据传感系统及其算法研究[D].南京航空航天大学,2004,12.
[2] 李清东,王伟,任章.FADS压力传感器冗余配置研究[J].计算机仿真,2008,25(11):48-51.
[3] Stephen A Whitmore,Brent R Cobleigh,Edward A Haering.Design and calibration of the X-33 flush airdate sensing system [J].NASA/tm-1998-206540,Dryden Flight Research Center Edward,California,1998:1-30.
[4] Currie I G Fundamental mechanics of fluid[M].McGraw-Hill Book Company,NewYork,1974Brent R.Cobleigh,Stephen A.Whitmore,Edward A.
[5] Haering Jr.Flush sirdate sensing(FADS)system calibration procedures and results for blunt forebodies[R].Systems and Technologies Conference and 3rd Weakly Ionized Gases Workshop 1-5,November,1999:1-27.

