亏损结构振动方程的稳态响应求解
张 淼
(长春工程学院 理学院,吉林 长春 130012)
0 引言
系统的运动方程总是在一定的坐标系中用坐标的微分方程[1]来描述的,设法使一组本来耦合的方程组变为一组无耦合的方程组,使每一个方程中只有一个待求的坐标,每个微分方程便可独立求解,称为工程结构振动微分方程的解耦[2].
若系统的特征值全不相同,则称为单频结构系统,若系统有重特征值,但重特征值的几何重数与代数重数相符,则对应的振动系统称为重频完备系统,若系统有重特征值,但重特征值的几何重数小于代数重数,则对应的振动系统称为重频亏损系统.在很多结构系统中即使出现密频或重频的问题,在讨论中一般都假定系统为完备系统从而进行动特性分析[3-6].但在亏损振动系统,这个过程的研究发生了困难,如非比例阻尼矩阵,或在非保守力作用下的结构动力问题,气动弹性颤振分析,以及结构和控制系统相耦合的问题,其相应的矩阵可能是亏损的[7].对亏损系统目前较好的方法是利用广义模态理论[8-9]实现非经典系统的优化与控制.本文考虑引入广义模态的伴随向量系[10],从而满足一定程度的规范正交化条件,来求解简谐激励下亏损结构振动方程的稳态响应.
1 基本理论
描述自由度为N的线性阻尼离散系统的自由振动方程为

(1)
相应地其强迫振动方程为

(2)
式中M,C和K∈RN×N分别为系统的质量、阻尼和刚度矩阵,它们为非对称矩阵.结构有限元分析时,作拉普拉斯变换x(t)=uest=ueiωt(s=iω)代入(1)式可得(s2Mu+sCu+Ku)est=0.考虑阻尼系统复特征对(si,ui)(i=1,2,…,2N)满足方程
(3)
对于N自由度振动系统,特征方程det[s2M+sC+K]=0有2N个呈复共轭对出现的特征值s1,s2,…,s2N(si∈C,其中si+1为si的共轭(i=1,3,…,2N-1)),称为系统的复频率.这些频率对应着一组呈复共轭对出现特征向量u1,u2,…,u2N(ui∈CN,其中ui+1为ui的共轭(i=1,3,…,2N-1))称为系统模态向量.
对线性振动系统的运动方程(1)式,设
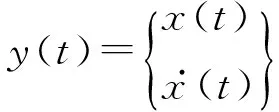
(4)
代入方程(1),则该二阶系统将转化为如下一阶系统:
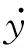
(5)
其中
称为系统的状态矩阵.
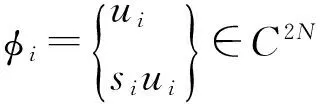
在A的Jordan标准形中,设对应于si(i=1,2,…,r)的Jordan块有r种不同的阶数,即
J=diag(J1,J2,…,Jr) (1≤r (6) 式中 则A矩阵对应的Jordan特征问题为 AY=YJ (7) 其中Y=[y1,y2,…y2N],称为A的广义状态向量矩阵,它的列向量组称广义状态向量,又可称为广义模态向量.为了方便表述,设亏损系统的特征分布情况为s1=s2=…=sm=s(2≤m<2N),而其余基频sm+1sm+2,…,s2N均为单频的情形.由(7)式可得方程组 (8) 根据文献[2],由方程组(8)解得的y1,y2,…,y2N是线性无关的.若x1,x2,…,x2N为A的广义状态向量系的伴随向量系,记X=[x1,x2,…,x2N],则必有 XHY=E (9) 其中(·)H表示共轭转置.用XH左乘(7)式并利用(9)式即可得到广义状态向量及其伴随向量系关于矩阵A的加权规范正交化条件为 XHAY=J (10) 下面利用这些正交性(9)和(10)式,来解耦亏损系统的振动方程,并求解其稳态响应的解析解.对方程(2)建立状态方程 (11) 其中 引入坐标变换 y(t)=Yq(t) (12) 其中q(t)=(q1(t),q2(t),…,q2N(t))T为模态坐标向量,将(12)式代入状态方程(11)并左乘XH,则有 (13) 假定s1=s2=s3,而其余基频s4,s5,…,s2N均为单频的情形,由(6)式可知 根据正交关系(9)和(10)式,将(13)式化为 即 (14) (15) (16) (17) 其中{·}i代表向量{·}的第i维分量.若解出q(t),然后代入(12)式获得y(t),并由(4)式可知取前N维即为响应x(t).现在考虑如何求解q(t). 对微分方程(17)式,为了表达方便,记si=a,qi(t)=y(t),{XHf′(t)}i=b(t),(17)式可表达为 y′(t)-ay(t)=-b(t) e-aty′(t)-ae-aty(t)=-e-atb(t) 即为 [e-aty(t)]′=-e-atb(t) 两边积分得 因此可解得 即 (18) (16)式与(17)式的解法相同.若考虑简谐激励下的强迫振动响应,那么{XHf′(t)}i中的各分量不是零,就是正弦函数,因此(18)式是一个关于正弦与指数乘积形式的典型分部积分问题,在数学的计算上不存在困难,具体结果视{XHf′(t)}i的形式而定.将q3(t)代入(15)式,它仍然是一阶线性微分方程,与(17)式的解法类似.同样将(15)式中解出的q2(t)代入(14)式,它还是一阶线性,仍然与(17)式的解法类似.由此可见,已全部求解出q(t). 在工程领域中,特征向量最大的功能就是使系统的性质矩阵对角化,从而解耦系统的振动方程,以便求得工程师们最为关心的响应问题,这也是之所以振型迭加法广为应用的主要原因.而亏损系统的最大特点是重频,且其重频率所对应的特征向量的个数发生缩减,使之由特征向量构成的无关的状态向量的个数少于系统的自由度的2倍,导致系统的状态空间的基底,不能完全满足特征方程.换而言之,由于状态向量的缺失,使状态向量对状态矩阵的对角化性能变得不完整,特征向量的解耦性能退化.本文针对这个问题,引入亏损矩阵的Jordan特征方程和Jordan标准形理论,建立广义状态向量系来构成状态空间的基底,虽然没有将状态矩阵完全对角化,但其部分对角化的程度并未对解耦后的振动方程的求解带来太大的影响,因此通过广义状态向量及其伴随向量系的双正交性,推导出亏损结构振动方程的稳态响应,使目前对亏损系统的研究又向前推进了一步. [1]龚东山,刘岳巍,牛富俊.特征函数在高阶常微分方程特解计算中的应用 [J].吉林师范大学学报(自然科学版),2008,29(4):8~10. [2]李德葆,陆秋海.实验模态分析及其应用[M].北京:科学出版社,2001. [3] Abe M.Vibration control of structures with closely spaced natural frequencies by a single actuator [J].Journal of Vibration and Acoustices,1998,120(1):117~124. [4]刘一武,张洪华,吴宏鑫.可控性差的空间密集模态的结构的振幅最优控制[J].自动化学报,2002,28(2):1~6. [5]Sun H L,Zhang P Q,Chen H B,et al.Active control of a structure with continuously closely spaced natural frequencies [J].Journal of Sound and Vibration,2006,294:15~22. [6]徐博候,鲍荣浩,张阿平.密频系统振动控制的状态估计[J].力学学报,2000,32(5):606~612. [7]张慧生,王文亮,张振宇.亏损特征值问题的摄动分析[J].复旦大学学报(自然科学版),1997,36(2):121~129. [8]时国勤,诸德超,王俊奎.线性振动亏损系统的广义模态参数的识别方法[J].固体力学学报,1991,12(3):235~241. [9]徐 涛,于 澜,鞠 伟,等.线性振动亏损系统广义模态灵敏度的逐层递推演算方法[J].力学学报,2008,40(2):281~287. [10]于 澜.亏损矩阵的广义特征向量系的规范正交性[J].长春工程学院学报(自然科学版),2012,13(4):123~125. [11]张 淼,于 澜,鞠 伟.亏损振系广义状态向量灵敏度的移频算法[J].计算力学学报,2013,30(6):872~878. [12]方保镕,周继东,李医民.矩阵论[M].北京:清华大学出版社,2004.2 亏损系统振动方程稳态响应求解
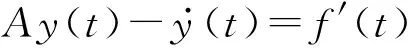
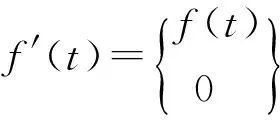
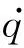
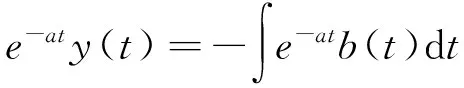
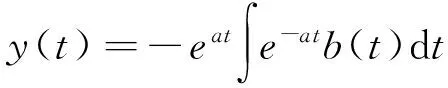
3 结论

