四象限电机控制器直流侧PWM 整流器变系数控制策略

姜卫东，李王敏，佘阳阳，吴志清

(合肥工业大学，安徽合肥23009)

电压外环的传递函数为式(6)，PWM 整流器输出电压与输入电流之间的传递函数:

0 引 言

目前，能源短缺已成为人类面临的重大难题之一。据统计，我国电动机的年用电量约占全国总发电量的65% ～70%。常规的电机驱动器的电源是由不控整流得到的，不能实现能量的回馈，也不能实现电机的四象限运行，同时对电网产生污染。因此研究电机节能系统具有重大的现实意义和深远的可持续发展的意义。

电压型PWM 整流器不仅能实现AC/DC 的电能变换，而且具有实现能量双向流动、低输入电流谐波含量、功率因数可控、输出电压可控等优点，是一种“绿色能源变换器”，得到越来越多的应用［1］。PWM 整流器控制策略一直是学术界关注和研究的热点，其控制策略主要包括基于电流闭环的矢量控制［2］、负载电流前馈控制［3］、直接功率控制策略［4］等。其中，基于同步旋转d－q 坐标系的电流－电压双闭矢量控制具有控制简单、稳定性和快速性较好等优点，因此得到了广泛的应用。

PWM 整流器在基于同步旋转d－q 坐标系的电流－电压双闭环矢量控制中，双闭环多采用PI 调节［5－7］，传统的PI 调节器存在稳定性和快速性相互制约的问题。增大PI 调节器中的比例系数可以提高系统的快速性，但系统的稳定性会受到影响。

本文介绍了三相PWM 整流器的数学模型和电流－电压双闭环控制［8］，在此基础上提出了变系数的PI 调节器。最后将此种控制方法实验，实验结果验证了此种控制算法的正确性和有效性。

1 PWM 整流器的控制模型

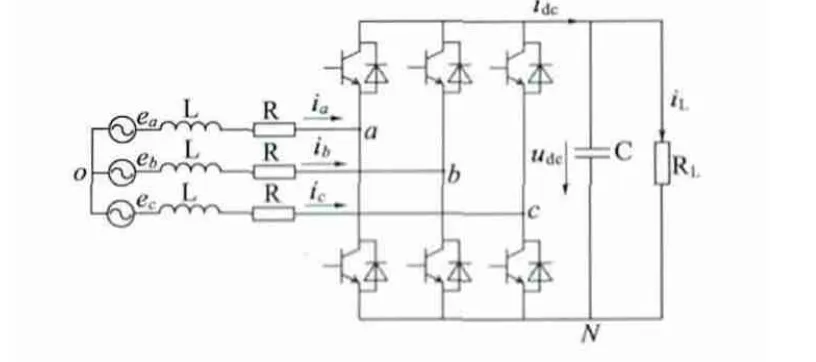
图1 三相电压型整流器主电路拓扑图

图1 为三相电压型PWM 整流器的拓扑图。其中ea、eb、ec为三相交流输入电网相电压;L、R分别为三相交流侧输入电抗的电感值和寄生电阻值;udc为直流侧电压;C 为直流侧电容;RL为直流侧负载;iL为负载电流;ia、ib、ic为整流器交流侧输入电流。Sk(k=a，b，c)为桥臂k 开关管开关逻辑。定义单极性二值逻辑开关函数:

假设三相交流电压对称，并忽略三相交流线路中电阻、电感的不对称性，根据基尔霍夫电压、电流定律和三相对称电压、电流之间的关系，得到三相电压型整流器在三相静止坐标系上的开关函数模型:

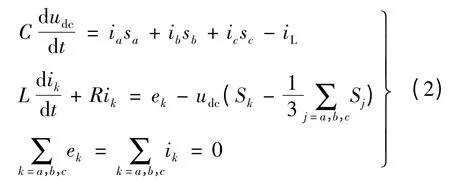
通过Clarke 变换和Park 变换，得到整流器在同步旋转d、q 坐标系下的数学模型，实现对三相电流的无静差跟踪。即:

式中:ed、eq为在d、q 坐标系下的电网电压;id、iq为在d、q 坐标系下的电网电流;Sd、Sq为在d、q 坐标系下的单极性二值逻辑开关函数;ud、uq为在d、q 坐标系中交流侧输入电压;ω 为电网电压的角频率。

2 PWM 整流器解耦控制算法

选取d 轴与电网电动势重合，则d 轴为有功分量参考轴，q 轴为无功分量参考轴。通过独立控制d轴与q 轴电流，实现有功和无功的独立控制。

在d、q 坐标系中，有功电流与无功电流相互耦合，任何轴上电流的变化都会引起另一轴上电流的变化。所以一般的PI 调节器很难达到理想的控制效果，为此将检测到的电流进行前馈，实现电流的解耦控制。忽略式(3)中的电阻，采用PI 调节，得到如下控制方程:

式中:kiP和kiI为电流PI 调节器的比例系数和积分系数分别为d 轴和q 轴电流给定值;有功电流给定值与负载电流成正比，其值为电压外环调节器的输出与功率因数φ 有关，d、q 轴电流给定值:

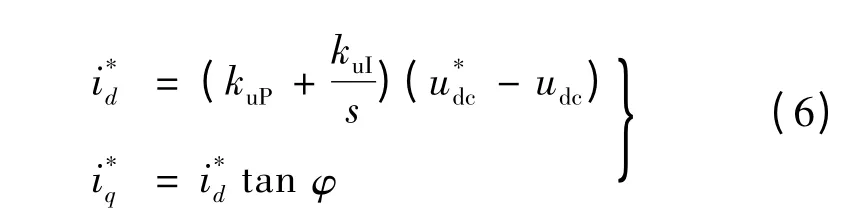
式中:φ 为功率因数角;kuP，kuI为电压PI 调节器的比例系数和积分系数;u*dc为直流侧电压给定值。图2为PWM 整流器的电流解耦控制图。通过设置有功、无功电流比率来控制三相电压型整流器的功率因数，当PWM 整流器在单位功率因数下工作时=0。

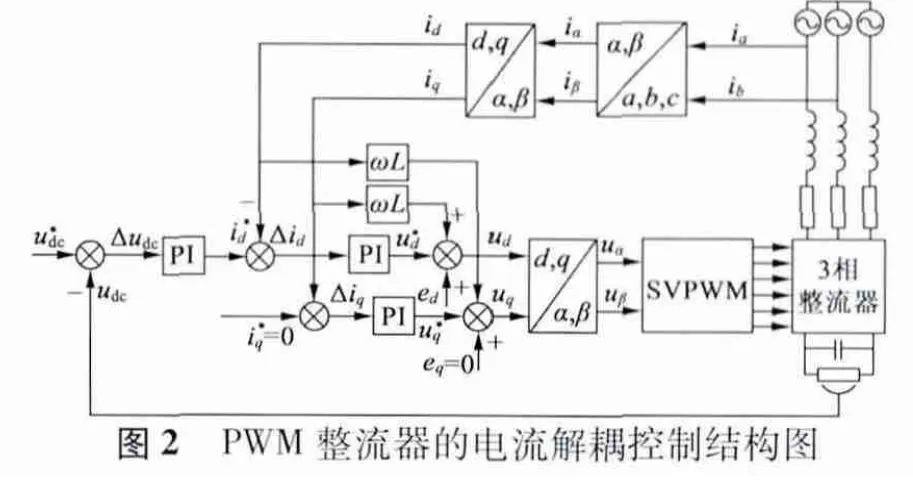
3 PWM 整流器的变系数PI 调节器的设计

PWM 整流器的变系数调节器的设计分为两步，首先按照电流－电压双闭环PI 设计方法设计出调节器参数的基值，然后根据动态过程中误差的大小对电压外环比例系数进行调整。

3.1 电流内环的设计

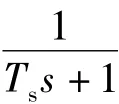
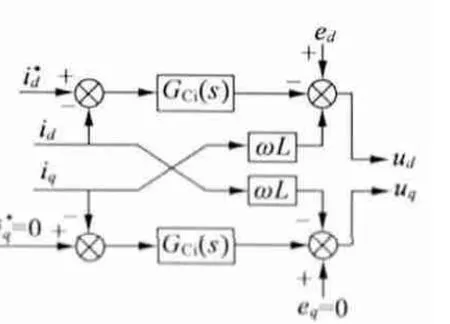
图3 PWM 整流器的电流内环控制框图

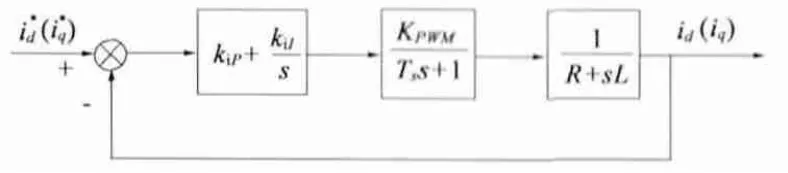
图4 简化的PWM 整流器电流环控制框图

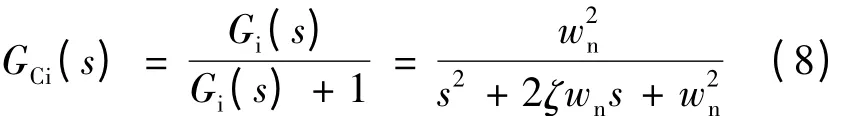
式中:

3.2 电压外环基值的设计

电压外环的传递函数为式(6)，PWM 整流器输出电压与输入电流之间的传递函数:

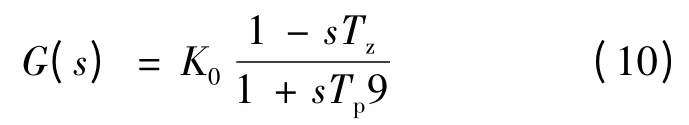
usm为网侧相电压幅值，ism为网侧输入相电流幅值。式(10)具体推导参考文献［9］。

图5 电压外环控制框图

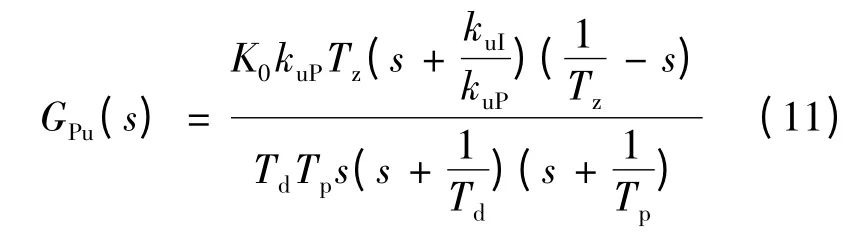
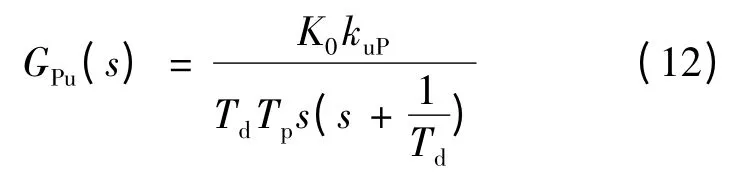
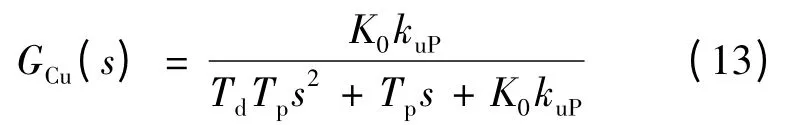
式中时，求得:

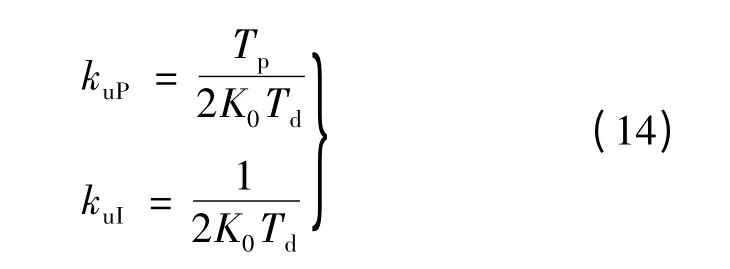
3.3 变系数电压外环PI 参数的设计

图6 为外环采用变系数的系统控制框图。设变

图6 外环变系数系统控制框图

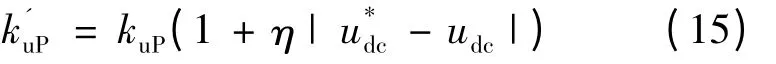
通过设定η 的值，改变电压外环在动态时的比例系数。

由图7 看出，不同的比例系数，系统的响应特性不同。电压误差可以认为是在输入侧加上了一个扰动信号，当误差较大时，误差变化相对较慢，持续时间较长，可以认为是一个低频输入扰动。在误差较小时，例如由于采样等原因引起的干扰，实际上是一个高频扰动。通过设计不同的PI 调节器来抑制不同频段的干扰信号。

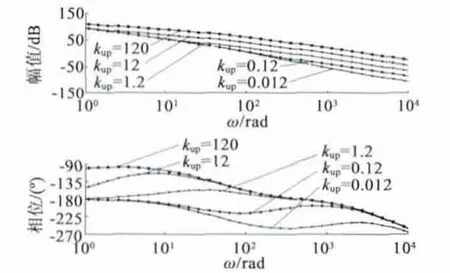
图7 电压外环不同比例系数下系统开环传递函数的Bode 图

从图7 中可以看出，采用较大的比例系数，系统的低频开环增益较大，有利于系统快速跟踪给定。系统对低频误差响应较快，但是在高频段增益也较大，不利于抵抗高频干扰。采用较小的比例系数，系统的低频开环增益较小，在高频段增益也较小，有利于抵抗高频干扰。

变系数PI 调节器的比例系数是随着误差变化的，当误差较大时，比例系数也较大，利用了系统的开环增益较大的特性，改善系统的快速性。当误差较小时，比例系数也较小，利用了此时控制系统开环增益较小的特性，改善系统的抗干扰能力。实际上，变比例系数的PI 调节算法就是在这一组Bode 图曲线中，根据误差的大小实现自动查找相应的控制系统增益曲线。

4 实验结果

为了验证所提出算法的有效性，搭建了实验平台，样机照片如图8 所示。样机主要参数如表1 所示。

图8 试验平台实物图

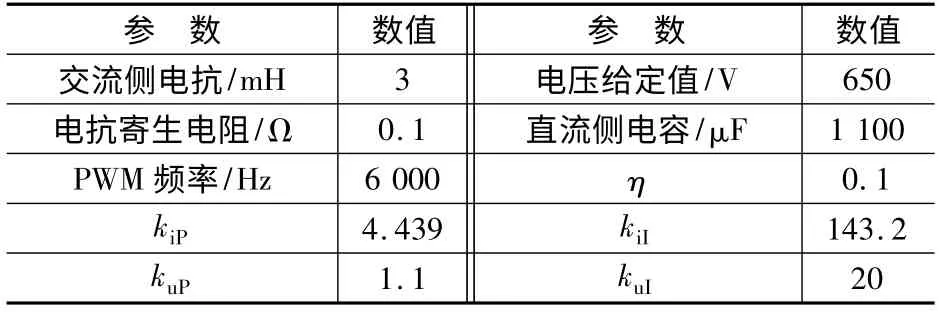
表1 样机主要控制参数表

4.1 PWM 整流器空载起动试验

图9 为PWM 整流器由不控整流进入PWM 整流的试验波形。图9(a)为采用定系数PI 调节器的试验波形，试验中直流侧电压最大升高了118. 75 V，调节时间大于82.4 ms，直流侧电压存在超调量。图9(b)为采用变系数PI 调节器的试验波形，整流器由不控整流进入到PWM 整流的过程中电压升高了92.5 V，调节时间小于28 ms，直流侧电压几乎不存在超调。

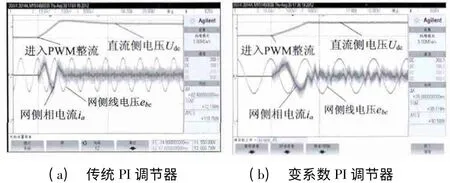
图9 PWM 整流器由不控整流进入PWM 整流的波形图

4.2 PWM 整流器突加负载实验

图10 为PWM 整流器突加负载试验波形，负载为100 Ω 的纯阻性负载，进入带载稳定后交流电流峰值为9.1 A。图10(a)为采用定系数PI 调节器突加负载实验波形，直流侧电压下降了约60 V，调节时间约为127.6 ms。图10(b)为变系数的PI调节器突加负载实验波形，直流侧电压下降了27.5 V，调节时间约60.2 ms。

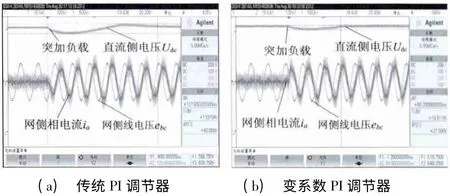
图10 PWM 整流器突加负载波形图

4.3 PWM 整流器整流突减负载实验

图11 为PWM 整流器突减负载试验波形。图11(a)为采用定系数PI 调节器突减负载实验波形，直流侧电压值波动为17. 5 V，调节时间为146. 8 ms。图11(b)为变系数的PI 调节器突减负载实验波形，直流侧电压没有出现明显波动，电流调节时间为51.8 ms。

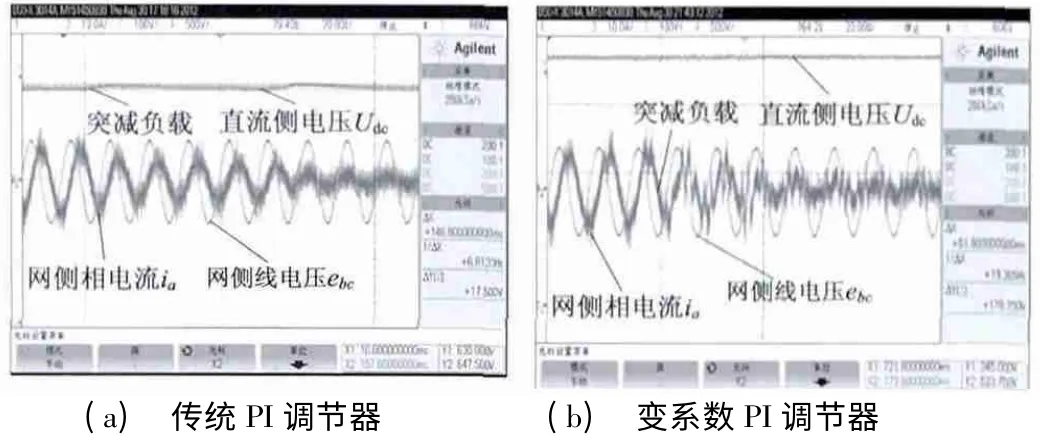
图11 PWM 整流器突减负载波形图

5 结 语

对比试验表明，采用变系数的PI 调节器获得比传统的PI 调节器更好的特性。采用变系数的PI 调节器获得更好的快速性、更小的超调量、甚至可以达到消除超调量的目的。采用变系数的PI 调节器可以保证系统在稳定性的基础上提高系统的快速性。

［1］ 张崇巍.PWM 整流器及其控制［M］. 北京:机械工业出版社，2003:20－110.

［2］ 张兴.采用新型PWM 控制的变频调速系统［J］. 电气传动，1997(3):21－24.

［3］ 倪靖猛，方宇，邢岩，等. 基于负载电流前馈的400 Hz 三相PWM 航空整流器［J］.电工技术学报，2011，26(2):141－146，164.

［4］ 王久和，李华德，王立明.电压型PWM 整流器直接功率控制系统［J］.中国电机工程学报，2006，26(18):54－60.

［5］ Bouafia A，Gaubert J P，Krim F.Predictive direct power control of three－phase pulsewidth modulation(PWM)rectifier using space－ vector modulation(SWM)［J］. IEEE Transaction on Industrial Electronics，2010，25(1):228－236.

［6］ Briz F，Degner M W，Lorenz R D. Analysis and design of current regulators using complex vectors［J］.IEEE Transaction on Industrial Applications，2000，36(3):817－825.

［7］ 陈耀军，钟炎平.基于合成矢量的电压型PWM 整流器电流控制研究［J］.中国电机工程学报，2006，26(2):143－148.

［8］ Blasko V，Kaura V. A new mathematical model and control of a three－phase AC－DC voltage source converter［J］.IEEE Transaction on Power Electronics，1997，12(1):116－123.

［9］ 陈大卓，姜建国.基于前馈解耦控制的电压型PWM 整流器可逆运行研究［J］.电气自动化，2008(6):45－48.