基于波形参数设计的认知雷达跟踪方法
杨 军,张 群,2,张景波,刘 明,邓冬虎
(1.空军工程大学信息与导航学院,陕西 西安710077;2.复旦大学电磁波信息科学教育部重点实验室,上海200433;3.中国电子科技集团公司第二十七研究所,河南 郑州450047)
0 引言
认知雷达是未来雷达系统发展的重要方向[1]。认知雷达通过对历史和当前环境的检测、分析、学习、推理和规划,可利用相应的结果自适应调整系统的接收和发射信号,使用最适合的系统配置,达到与外部环境和目标状态相匹配,可以实现获取最佳的系统性能[2]。
作为认知雷达的重要分支,认知跟踪雷达已成为目前的研究热点之一。认知跟踪雷达利用认知雷达完成对目标的跟踪,通过目标状态等先验信息设计发射波形,雷达从经目标和环境返回的回波中提取出新的目标和环境信息作为下一发射时刻的先验信息,并以此为依据设计新的发射波形,由此完成对目标的跟踪。文献[3]系统地介绍了认知跟踪雷达,通过认知波形选择,以目标跟踪误差最小为准则,利用容积卡尔曼滤波实现了目标认知跟踪。文献[4]利用正交频分复用(OFDM)信号提出了基于后验克拉美罗界(Posterior Cramér-Rao Bounds,PCRB)的波形设计方法,可在多径环境下有效实现目标的跟踪。文献[5]结合接收端最大信噪比准则分析了多目标环境中的认知雷达目标跟踪问题。现有的雷达对机动目标进行跟踪时,存在跟踪误差大、不能充分利用环境信息的问题。针对此问题,本文提出了基于波形参数设计的认知雷达跟踪方法。
1 跟踪问题建模
1.1 量测模型
假设ET为发射信号的功率,fc为载频,则雷达的发射信号为:
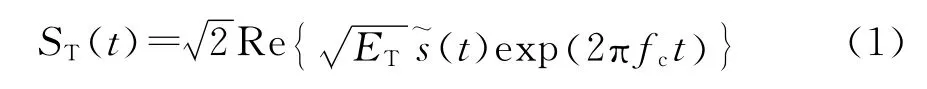
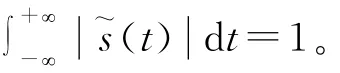
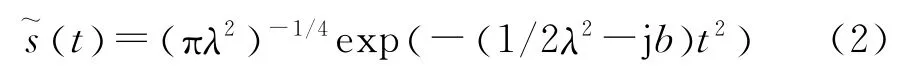

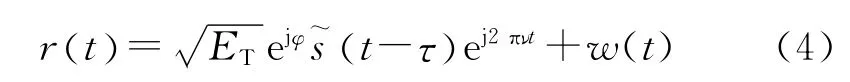
以ts=1/fs=T/N 为采样间隔对回波信号进行采样,有:
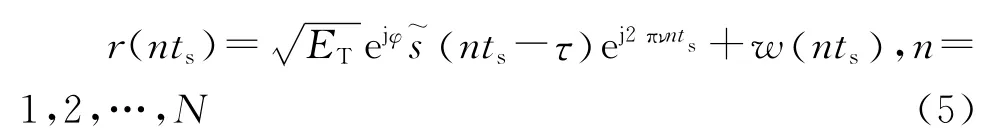
1.2 状态模型

当目标沿着线性轨迹运动时,可以将状态转移矩阵H 表示为:

式(8)中,Δt是运动状态采样间隔。状态演化噪声vk为零均值高斯随机变量,协方差为Σe的高斯分布:
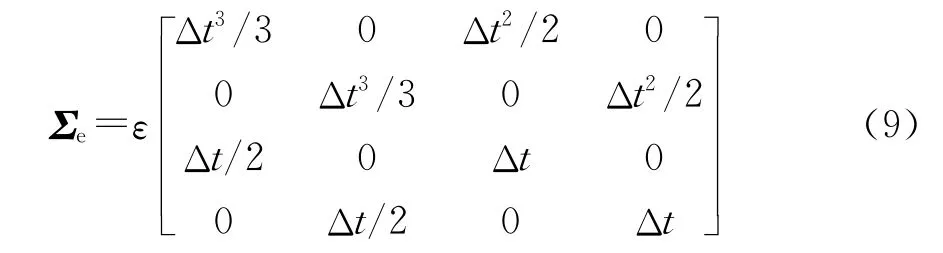
式(9)中,ε是表示目标的噪声强度。
1.3 目标跟踪算法
本文量测方程(6)中的矩阵SU 是目标运动状态εk的非线性函数矩阵,即SU=f(εk),使得无迹卡尔曼滤波或者容积卡尔曼滤波不能很好地跟踪上目标,因此这里采用粒子滤波实现目标跟踪。另外,考虑到提高计算效率,解决粒子贫乏问题,增强目标的跟踪性能等因素,因此,本文采用粒子群优化粒子滤波实现目标的跟踪。
粒子群优化滤波方法的基本原理是:将最新观测值融合到采样过程中,并对采样过程利用粒子群优化算法进行优化,使粒子集朝着高似然区运动[6-7]。具体跟踪算法如下:
1)首先将最新的量测值引入到采样过程,并定义适应度函数:
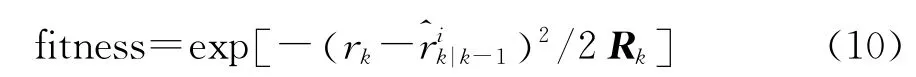

2)初始化。初始时刻,从重要性函数采样N 个
3)计算重要性权值:

第i个粒子从初始状态到当前迭代次数搜索最优值为个体极值Ppbest,种群从初始状态到当前迭代次数搜索最优值为全局极值Pgbest,根据最优值通过
式(12)、式(13)更新每个粒子的速度和位置。


对权值归一化处理得到

4)重采样:为了解决粒子退化问题,选择和复制较大权值的粒子,将带有权值的样本映射为等权值样本。
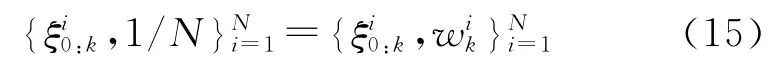
2 认知雷达波形参数设计理论
在利用认知雷达跟踪目标时,常用波形设计准则有最大信噪比准则、互信息准则、PCRB 准则等,输出信噪比是反映雷达性能的一个重要参数,雷达的跟踪性能和信噪比有着密切联系,但是点目标高斯白噪声情况下的输出信噪比与发射波形无关,互信息准则必须满足目标冲激响应已知的条件,而PCRB准则具有适用范围广,设计精度高的特点,不受以上制约的影响。综合考虑,本文选择了基于PCRB的波形参数设计方法。
关于目标运动状态向量ξk的PCRB可以表示为:

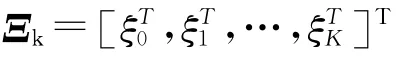
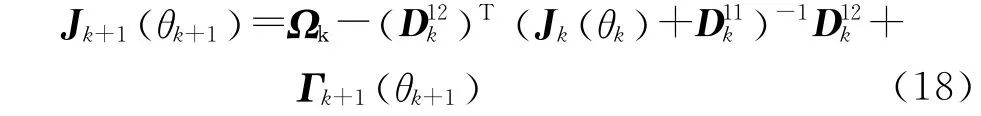
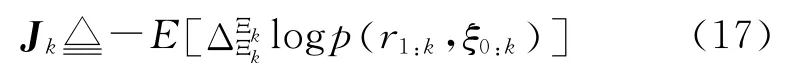
其中,
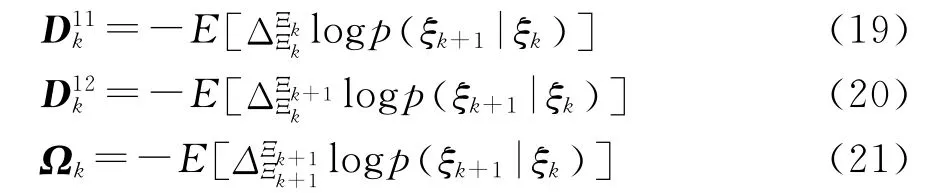

波形参数θ仅仅出现在量测方程(6)中,因此,在FIM 递推方程(18)中,只有Γk+1θk( )+1与波形参数θk+1相关,在波形参数θk+1设计的过程中,只用考虑Γk+1(θk+1),考虑到充分利用历史观测值r1:k,重新定义:
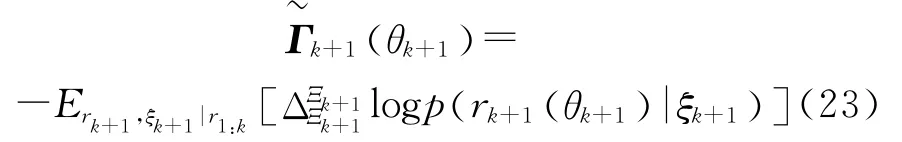
于是最优波形发射参数为:

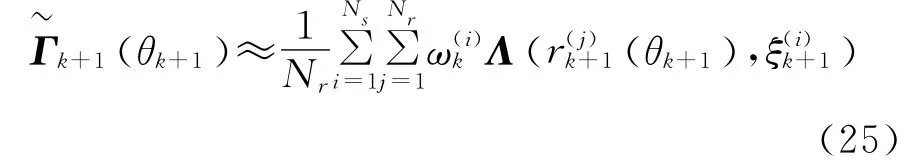
于是基于PCRB的波形参数为:
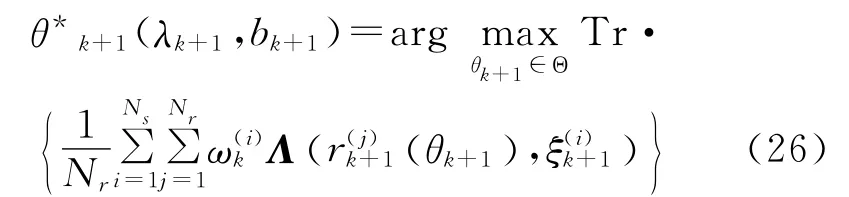
由此完成对认知跟踪雷达发射波形的设计。
3 仿真与分析

表1 仿真参数设置Tab.1 Values of parameters forsimulation
此处进行了Nm=100次蒙特卡罗仿真,距离和速度的估计的均方根误差(RMSE)分别定义如下:

其中x、x·、y、y·、x^i、y^i、^x·i、^y·i分别表示目标 的 运 动状态以及第i次蒙特卡罗仿真的估计运动状态。
图1和图2分别示出了目标的距离和速度估计情况与迭代次数的关系。由图1可知,基于自适应设计的波形能够较好地跟踪上目标,而传统固定波形设计在迭代更新次数大于14之后出现明显误差。由图2可知,基于自适应波形设计的RMSE(距离、速度)小于传统固定波形设计,且自适应波形设计对速度跟踪的RMSE 趋于稳定,而传统波形设计对速度跟踪的RMSE 有变大的趋势。从仿真结果得到自适应的波形设计可以有效地实现对目标的跟踪。
本文算法充分利用历史观测值,在认知雷达发射端通过利用PCRB 准则来设计认知跟踪雷达的发射波形,在接收端利用粒子群优化粒子滤波算法来对目标状态进行有效估计,从而最大程度上降低雷达系统对目标跟踪精度的PCRB,改善了目标的跟踪性能。仿真结果验证了该算法的有效性。
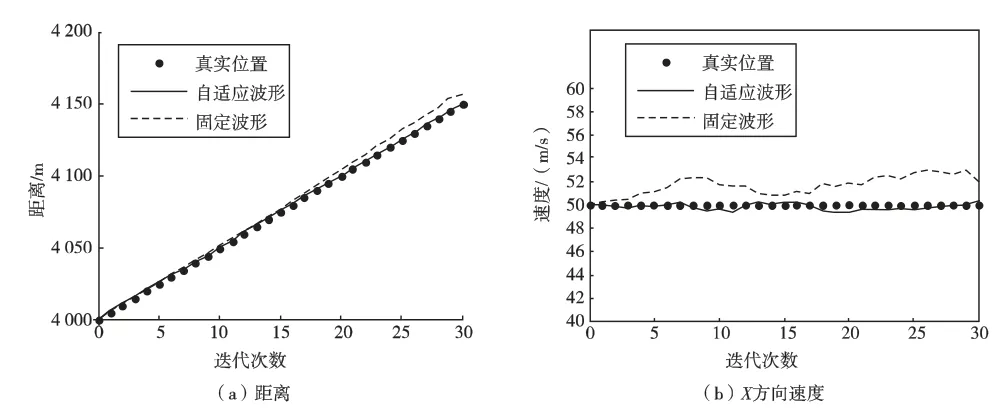
图1 认知波形和固定波形跟踪轨迹与迭代次数关系Fig.1 Comparison of tracking results for cognitive and fixed waveform

图2 认知波形和固定波形RMSE与迭代次数关系Fig.2 Comparison of RMSE for cognitive and fixed waveform
4 结论
本文提出了基于波形参数设计的认知雷达跟踪方法,该方法利用目标的运动状态和发射波形参数联合构建系统量测模型和状态模型,在系统发射端采用优化PCRB设计了自适应发射波形参数,降低了对目标跟踪精度的PCRB,在接收端考虑到传统的粒子滤波容易陷入局部最优,对粒子数目要求大等问题,采用了粒子群优化的粒子滤波来对目标进行跟踪,最后以二维空间中匀速运动点目标为实验模型。仿真表明,相比于传统固定波形设计,本文所提方法很大程度上提高系统的跟踪精度。但是文中所设计的波形不能较好地抑制多径效应的影响,因此下一步研究拟结合压缩感知理论或者将单分量LFM 信号作为OFDM 信号的导频信号来完成复杂环境下目标的认知雷达跟踪。
[1]黄培康.遥感目标的特征提取与反演[R].长沙:国防科 技大学,2011.
[2]Haykin S,Cognitive radar:a way of the future[J].IEEE Signal Processing Magazine,2006,23(1):30-40.
[3]Haykin S,Zia A,Xue Y,et al.Cognitive tracking radar[C]// Proceedings of 2010 IEEE Radar Conference.Washington DC:IEEE,2010:1467-1470.
[4]Chavali P,Nehorai A.Cognitive Radar for Target Tracking in Multipath Scenarios[C]//Proc.Int Waveform Diversity Des.Conference.Niagara Falls,Canada:WDD,2010:110-114.
[5]崔琛,张鑫.多目标环境中的认知雷达跟踪方法[J].信号处理,2013,(29)1:107-114.
[6]方正,佟国峰,徐心和.粒子群优化粒子滤波方法[J].控制与决策,2007,22(3):273-277
[7]朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010.
[8]Tichavsky P,Muravchik C H,Nehorai A.Posterior Cramér-Rao bounds for discrete-time nonlinear filtering[J].IEEE Trans Signal Process,1998,46(5):1386-1394

