基于双线导线的磁干扰计算与优化设计方法

杨振宇，林春生

（海军工程大学兵器工程系，湖北 武汉430033）

0 引言

光泵磁强计是一种高分辨率、高精度、高稳定性的磁强计，在航磁测量、地磁导航定位等领域有着广泛的应用［1-2］。在安装空间狭小的高速运动载体上用光泵进行磁场实时测量时，必须首先掌握磁测装置受载体电磁环境影响规律，在此基础上通过载体磁优化设计，为测量系统提供一个良好的工作环境，保证磁场测量精度。为了保证系统的正常工作，必须要对设备进行供电，载流导线产生的磁场是载体内部主要干扰源之一。直流双线供电是测量系统最常用的供电方式［3］，双线导线磁干扰量级很小［4］，对于探头安装在尾椎末端大型固定翼载体可以不考虑，但对于小型运动载体［5］，光泵探头难以做到远离导线安装，必须设法通过优化布线和合理选择光泵探头安装位置等措施将导线磁干扰降低到要求的范围以下。准确计算导线的磁场有助于了解导线磁干扰规律和为载体平台的磁环境优化设计提供参考，Alksne的双线导线磁场模型［6］只分析了轴向磁场，其双平行线公式是在双绞线公式基础上取极限得到的，且为了便于对比分析使用了许多归一化的假设。本文针对此问题，提出了基于双线导线的磁干扰计算与优化设计方法。

1 双绞导线磁场建模与计算

当光泵探头距离导线较近时可以将导线简化为无限长模型，设双绞导线在周围任意点P 产生的磁场为Bt，建立直角坐标系如图1所示。图中Z 轴为双绞线的轴线，XOY 面为过P 点和Z 轴垂直的平面，该平面和两线交点的连线为X 轴。设双绞导线的轴距为2d，螺距为p，当2d≪p 时，电流可近似认为是沿Z 方向的［6］，设线i（i=1、2）通过电流为Ii，根据毕奥-萨伐尔定律，其在P 点产生的磁场：

式中，μ0=4π×10-7N／A2，Ri是P 点 到 电 流 元I1dz、I2dz之间的距离，ri是Ri在XOY 面的投影。

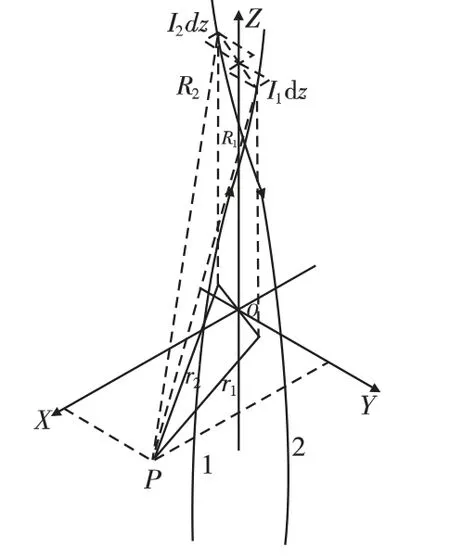
图1 双绞导线直角坐标系Fig.1 Rectangular coordinate system of twisted pairs

由安培定则可知Bt1和Bt2均在XOY 面上，如图2所示。将它们沿X、Y 轴分解可得双绞线磁场：

图2 双绞导线的XOY 平面Fig.2 XOYflat of twisted pairs

求解Bt即求解其两个分量Btx、Bty。为了便 于分析角度的影响，这里使用极坐标替换Alksne模型中的直角坐标，设OP 的长度为r，和Y 轴夹角为θ，旋度系数k=2π／p，由余弦定理可得：

计算式（2）中的三角函数得：

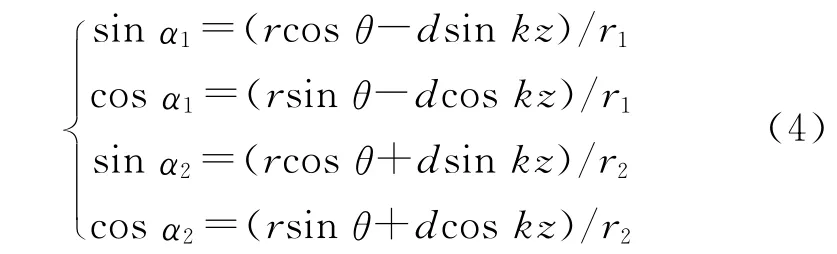
当I1=-I2=I时，将式（1）、式（3）、式（4）代入式（2），忽略二项展开式中包含d2的二次小项，化简整理得：

上式中奇函数的积分为0，利用贝塞尔函数计算偶函数的积分得：

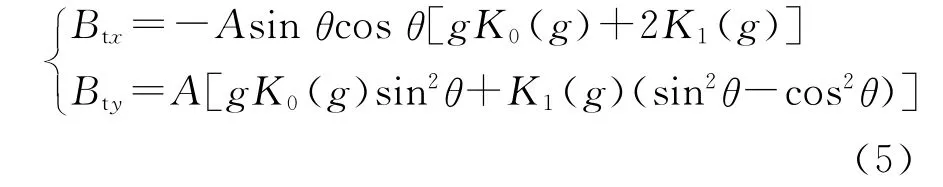
式中，g=2πr／p，A=2μ0dI／rp，K 是第二类修正贝塞尔函数。

2 双平行导线磁场建模与计算

参照计算双绞导线磁场的方法，设双平行导线的磁场为Bp，导线间距为2d，通过电流I1=-I2=I，在空间任意一点P 产生的磁场分别为Bp1、Bp2，由安培定则可知它们共面，以此面为XOY 平面，以两导线的连线为X 轴，建立坐标系如图3所示。图中r、r1、r2为点P 到O、I1、I2的径向距离，θ、α1、α2为OP、Bp1、Bp2和Y 轴的夹角。

双平行导线磁场：

由无限长直导线的磁场公式得：

由余弦、正弦定理可得：

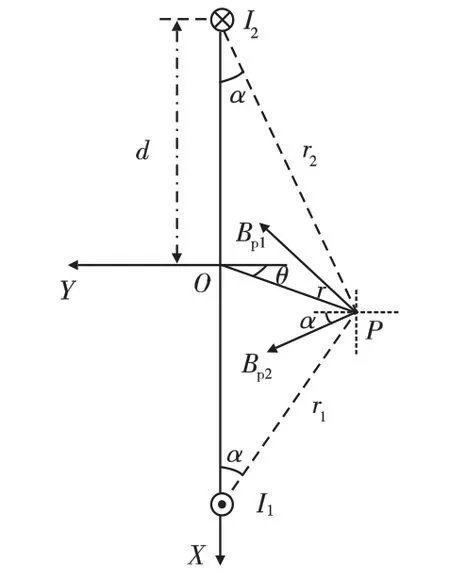
图3 双平行线的坐标系Fig.3 Rectangular coordinate system of parallel wire

为了便于与双绞线磁场比较，需要将r1、r2用r、θ替代，同样由余弦定理得：

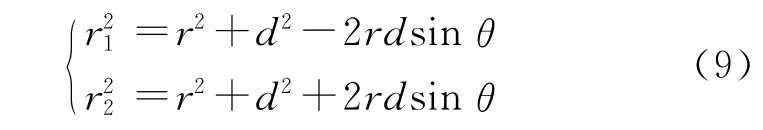
将式（7）-式（9）代入式（6）即可得到双平行导线的磁场：

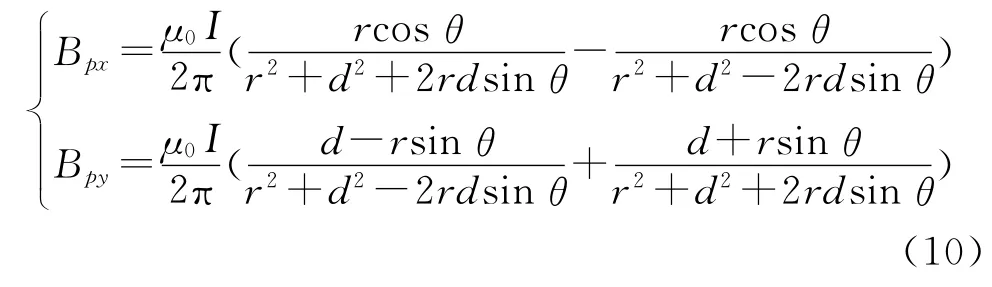
3 双线导线磁场影响因素分析

根据式（5）、式（10）可以将双线导线磁场的影响因素分为电流、测点位置、导线参数三大类，其中测点位置包括测点到导线轴线的径向距离r和夹角θ，导线参数包括导线轴距（或间距）d 和螺距p，两类导线的磁场均与I、r、θ、d 四个变量有关，双绞线还与p 有关。可以证明两类导线磁场都与电流I成正比，为简化分析，下面的分析中均设定I=1A。

3.1 双线导线磁场与测点位置（r、θ）的关系分析

设定d=1cm，p=10cm，取r=10cm，导线磁场与夹角θ的关系如图4所示，由于建立的模型均是对称，θ只需在0°～90°范围内取值。

由图4可见两类导线磁场都随θ增大而增大，Y轴方向的磁场最大。对比图4（a）、（b）可见双绞导线受θ的影响比双平行更明显。d、p 取值不变，θ分别取0°、45°、90°时对应的导线磁场沿径向分布如图5所示。

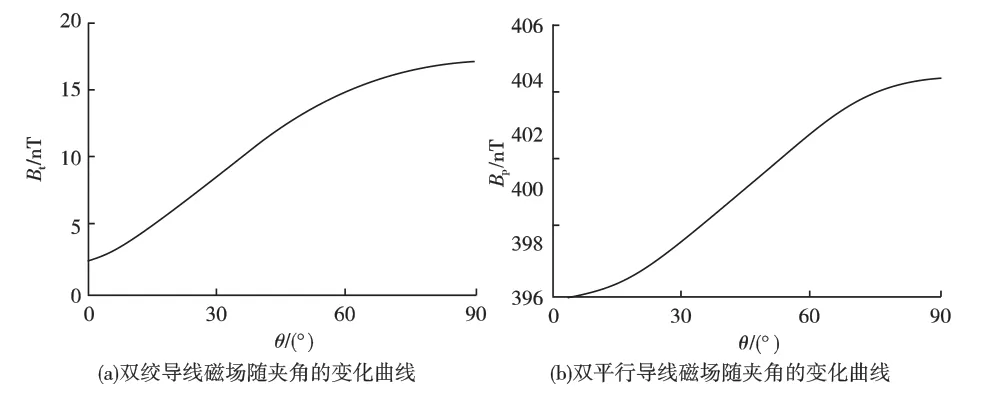
图4 双线导线磁场与夹角θ的关系分析Fig.4 Relationship between magnetic field of two wires andθ

由图5可见两类导线的磁场随r的增加迅速下降，双绞导线的下降速度更快，由于双线导线磁场随距离增大衰减很快，故综合比较r 比θ 对导线磁场的影响更明显。

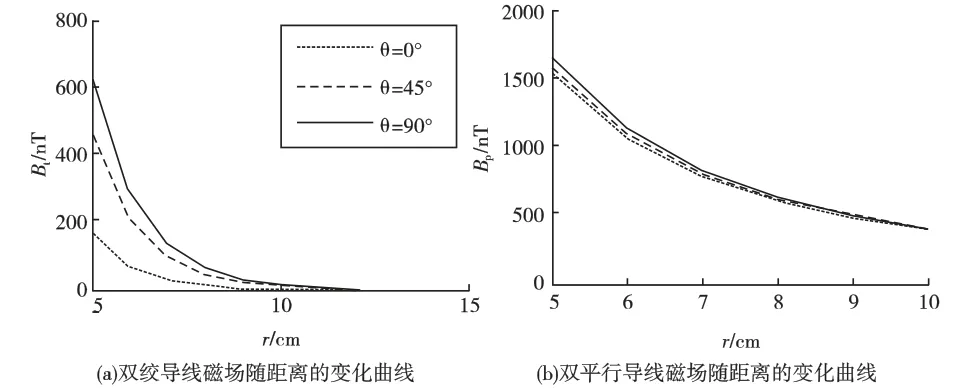
图5 双线导线磁场沿径向分布规律Fig.5 Relationship between magnetic field of two wires and r

3.2 导线磁场和导线参数（d、p）的关系分析

取p=10cm，r=10cm，θ=90°，双线导线磁场和导线轴距／间距d 的关系如图6所示。

图6 双线导线磁场和轴距／间距d 的关系分析Fig.6 Relationship between magnetic field of two wires and d

可见两类导线磁场均与d 成反比。设定d=1 cm，r=10cm，θ分别取值0°和90°时双绞导线磁场与p 的关系分析如图7所示，图中的直虚线为相同参数对应的双平行导线的磁场。

图7（a）中，当θ=0°时双绞导线的磁场随着p增大而逐渐趋向于双平行的，但当θ=90°时，图7（b）中出现双绞线磁场更大的情况，其交点对应横坐标为p=0.57m，计算可得当r／p＜0.175时，双绞线磁场比相同参数的双平行线磁场大，这一结论与文献［6］的归一化计算结果相同。

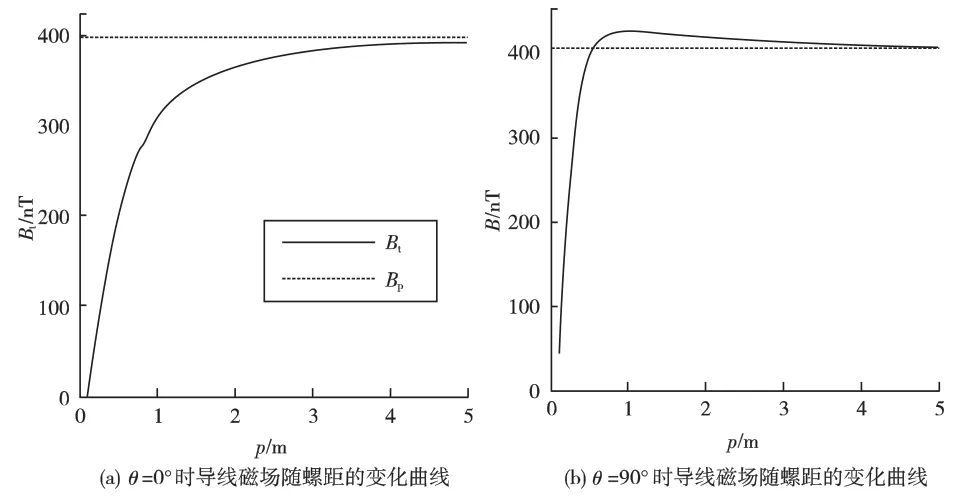
图7 双线导线磁场和螺距p 的关系分析Fig.7 Relationship between magnetic field of two wires and p

4 应用实例分析

已知导线参数d=0.5cm，p=0.3m，要求给出测点位置处的导线磁场干扰小于10nT 的电流控制与测点位置选择的磁环境优化设计方案。由前面可知导线磁场与角度有关，为了简化分析，取磁场最大时对应的θ=90°，当I=1A 时，由式（7）计算得到的单线导线磁场Bs和由式（10）、式（5）计算得到的双线导线磁场Bp、Bt沿径向分布如表1所示。

表1 导线磁场沿径向分布Tab.1 Radial distribution of magnetic field

由表1可见，双线制导线磁场远小于单线的。当供电电流大小为1A 时，为保证测点的磁干扰低于10 nT，采用双绞线布线时要求光泵的安装位置与导线的径向距离r＞20cm，双平行布线时要求r＞45cm。

由于导线磁场和电流成正比，故当光泵与导线的径向距离已知时，如r=10cm，则为满足磁环境优化的指标要求，对于双绞线，允许的最大电流为r／140.8≈71mA，双平行线的则是r／200.5≈50mA。

根据前面的分析结论，在运动载体上进行磁场测量时，降低导线磁干扰的载体磁环境优化设计方法可总结如下：

1）尽量使用双线供电取代单线，一般优先选择双绞线，注意当角度和双绞线的轴距取值较大时，可能会出现双绞线磁场更大的情况。

2）安装探头首先应当尽量使测量点远离导线，当测点距离导线较近时，应尽量使测点在两导线的延长线（X 轴）方向，避免测点位于两导线的轴线（Y轴）方向。

3）设计布线时应当尽量减小电流，对于双平行导线，尽量减小其间距，对于双绞导线，需要尽量减小其轴距和螺距。

5 结论

本文提出了基于双线导线的磁干扰计算与优化设计方法，该方法与以前的Alksne模型相比，使用了精确的双平行磁场公式，分析了角度的影响。实例分析表明研究结论可以为优化布线和合理选择测点位置等载体磁环境优化措施提供理论依据和参考。本文只研究了无限长双线导线的磁场与优化设计方法，拟对半无限长以及有限长两种情况的导线磁干扰进行研究。

［1］伍东凌，陈正想，王秀.基于遗传算法的磁干扰补偿方法［J］.探测与控制学报，2012，34（6）：16-20.

［2］谭斌，林春生，张宁，等.地磁场梯度对飞机磁场求解精度的影响分析［J］.武汉大学学报（信息科学版），2011，36（12）：1482-1485.

［3］金华标，吴军，李鹤鸣.船用电子设备电磁兼容性设计［J］.武汉理工大学学报（交通科学与工 程版），2009，33（3）：479-482.

［4］Piper G R，Jr A P.Magnetic Flux Density Produced by Finite-Length Twisted-Wire Pairs［J］.IEEE Tran on Electromagnetic Compatibility，1996，38（1）：84-92.

［5］胡正东，郭才发，张士峰，等.Unscented卡尔曼滤波在飞航导弹地磁导航中的应用［J］.宇航学报，2009，30（4）：1443-1448.

［6］Alksne A Y.Magnetic Fields near Twisted Wires［J］.IEEE Trans on Space Electron and Telemetry，1964（10）：154-158.