用于多普勒回波去噪的双重指数型阈值函数
张 翔,王海彬,杨军超
(1.西安机电信息技术研究所,陕西 西安710065;2.机电动态控制重点实验室,陕西 西安710065)
0 引言
小波变换[1]的概念是由法国工程师J.Morlet在1974年首先提出的。近年来,小波变换理论得到了非常迅速的发展,特别是在信号分析所涉及的去噪、压缩、传递等领域[2]。在信号去噪领域中,Donoho和Johnstone[3]提出了小波阈值去噪的方法,他们研究的是在叠加性高斯白噪声环境下检测出真实信号的情况,获得了非常好的去噪效果。
滤波器去噪是实际应用最广泛的一种方法,但时常在滤除噪声的同时导致了有用信号的失真,它是从纯频域的角度来分析和消除噪声。在常用的基于傅里叶变换的信号去噪方法中,总是使得信号和噪声的频带重叠部分尽可能小,这样在频域通过时不变滤波,就将信号和噪声区分开,但如果两者重叠区域很大时,就无法实现去噪的效果了。由小波变换的特性可知,高斯噪声的小波变换仍然是高斯分布的,它均匀分布在频率尺度空间的各部分,而信号由于其带限性,它的小波系数仅仅集中在频率尺度空间上的有限部分,利用正交小波变换和高斯随机变量的性质对信号的小波分解系数做阈值量化,就可以完成去噪的过程[4]。但是在阈值量化过程中,Donoho提出的阈值函数存在不连续或估计的小波系数和分解的小波系数存在偏差的问题,这些问题都会降低去噪效果。本文针对此问题,提出了双重指数型阈值函数对多普勒回波信号进行去噪处理。
1 小波阈值去噪算法和双重指数函数
1.1 小波阈值去噪算法
小波变换是一种信号的时-频分析,发展了传统的傅里叶变换思想,在时域和频域都具有良好的局部特性,特别是对非平稳信号的分析明显优于傅里叶变换。同时它具有多分辨率的特点,可以方便地从含有噪声的信号中提取原始信号,小波变换能将信号的能量集中到少数的小波系数上,而白噪声在任何正交基上的变换仍然是白噪声,其分量分布在大多数展开系数上[5]。相对来说,有用信号所对应的小波系数幅值较大,但数目较少,而噪声对应的小波系数是一致分布的,个数较多,但幅值小。基于这一思想提出了“硬阈值”和“软阈值”[6]去噪方法,即在众多小波系数中,把绝对值较小的系数置为零,而让绝对值较大的系数保留或收缩,得到估计小波系数,然后利用估计小波系数直接进行信号重构,即可达到去噪的目的。
因此,小波阈值去噪过程可分为以下三个步骤:
1)选择一个小波基函数,确定小波分解层数并对信号进行小波分解,得到一组小波系数。
2)确定阈值并选择合适的阈值函数对小波系数进行阈值处理。
3)小波重构。根据阈值化处理后的高频小波系数以及未处理的低频小波系数进行离散小波反变换重构信号。
在小波阈值去噪算法中,阈值函数的选取会直接影响小波阈值去噪的质量,因此一个完善的阈值函数对于小波阈值去噪是一个重要的因素。
常用的阈值函数有以下两种:
1)硬阈值函数
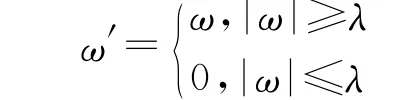
2)软阈值函数
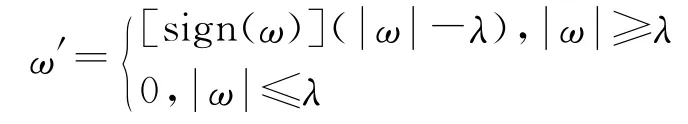
其中ω 是分解的小波系数,ω′是估计的小波系数,λ是指定的阈值。
1.2 双重指数函数
双重指数函数常规公式为:

当x<0 时,双重指数函数接近1,但当x>0时,双重指数函数成长速率比指数函数还要快,如图1为双重指数函数和一般实数指数幂的比较。

图1 双重指数函数和一般实数指数幂的比较Fig.1 Comparing of double exponential function and general exponential power
2 双重指数型阈值函数
阈值函数的作用是对小波系数作门限阈值处理操作,通常都是将较小的小波系数置零,将保留较大的小波系数或对较大的小波系数进行收缩处理。直接将较小的小波系数置零虽然能滤除大部分噪声,但是同样会滤去一定量的真实信号;如果直接保留较大的小波系数,会使去噪后的信号存在较多的尖峰,不够平滑;如果对较大的小波系数进行收缩处理,虽然能够使去噪后的信号更加平滑,但是收缩后的小波系数(即估计的小波系数)始终与分解的小波系数存在一个恒定的偏差,该偏差值大小等于阈值λ。阈值函数的连续性同样重要,硬阈值函数在│ω│=λ处是不连续的,容易引发伪吉布斯现象,即在不连续点四周的信号会在一个特定目标水平上下波动。
可以通过设计一个连续的新阈值函数解决上述问题。处理较小的小波系数时,为了保留真实信号的同时又最大程度地滤去噪声,可以对较小的小波系数进行收缩处理,考虑使用一个指数形式的系数来满足条件,类似2a,其中a是一个包含阈值λ 和分解的小波系数ω 的函数,当│ω│→0时,2a→0;处理较大的小波系数时,既要兼顾信号去噪后的平滑性,又要使估计的小波系数与分解的小波系数在数值上尽可能接近,这就要求当│ω│→∞时,2a→1,且2a向1逼近的速度要随着│ω│的增大而加快,这样才能够更好地减小估计的小波系数与分解的小波系数之间的偏差,使用双重指数形式的系数可以满足这个要求。

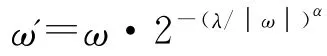
式中α为正整数。
所以该阈值函数是呈线性逼近ω′=ω 的,当ω增大时,ω′逐渐逼近ω,因此双重指数型阈值函数可以很好地解决软阈值函数中ω和ω′和恒定偏差问题。
双重指数型阈值函数不是分段的,相比传统的阈值函数更为简单。同时该阈值函数在对低于给定阈值的小波系数处理上同样具有优势,传统的阈值函数设定当小波系数的绝对值小于给定的阈值时,小波系数取零;双重指数型阈值函数对那些绝对值小于给定阈值的小波系数进行缩减处理,使得它们远小于其他系数,在一定程度上保留其包含的真实信号。调控参数α 越大,双重指数型阈值函数越近似于硬阈值函数,但是随着α的增大,计算量也会相应地增加。
3 仿真验证
3.1 使用三种阈值函数进行阈值处理
分别使用三种阈值函数对简单信号进行阈值处理,结果如图2所示。从图中可以看出,双重指数型阈值函数的处理结果最为平滑,而且相比软阈值函数的处理结果更能够保留一些真实信号中的尖峰特性。
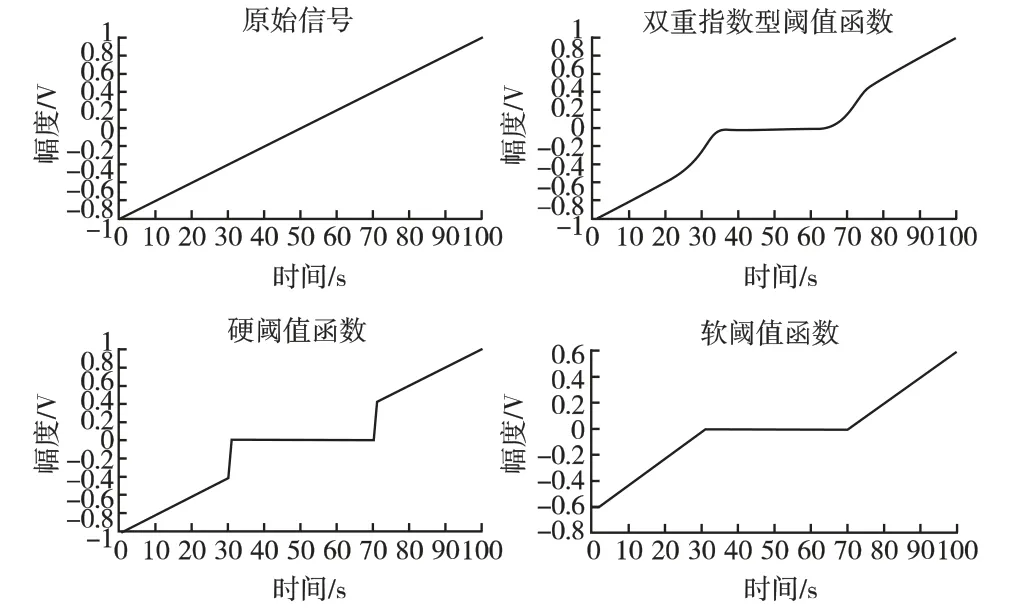
图2 三种函数阈值处理结果Fig.2 The results of three kinds functionthreshold processing
3.2 引信回波信号的模拟
考虑相对简单的情况:点目标静止,引信匀速直线运动,速度为V,点目标与引信运动方向垂直距离为H,设从引信工作起始点到离目标最近点长为R0,经过时间t后,引信运动至与距目标最近点相距R 处,具体如图3所示。
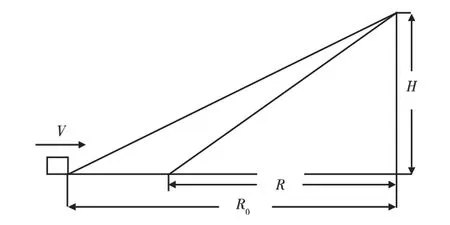
图3 引信工作历程图Fig.3 Fuze work process diagram
由图3可知R=R0-Vt,假设发射波形为f=sin(2πf0t),其中f0为载频,取15GHz。则回波可表示为:

脉冲多普勒雷达的发射信号是按一定的脉冲重复周期进行幅度调制的脉冲,因此多普勒频移表现为脉冲到脉冲的相移。若目标相对引信的径向速度为零,则经过模数转换后的回波信号为一等幅脉冲串;若目标相对引信的径向速度不为零,则经过模数转换后的回波信号为一经过余弦信号调幅的脉冲串,此余弦信号的频率即为多普勒频率,径向速度不同则多普勒频率也不同。
将回波信号与本振f=sin(2πf0t)混频再经低通滤波后,得到多普勒信号
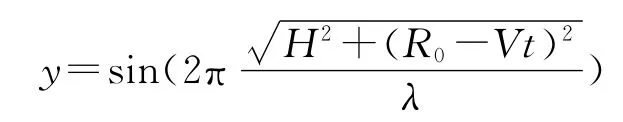
对相位求导得多普勒频率为:
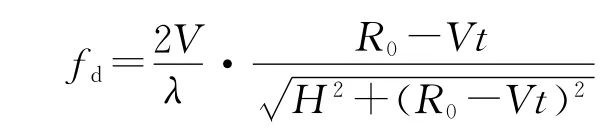


图4 模拟回波信号Fig.4 Simulate echo signal
3.3 去噪处理以及结果对比
3.3.1 去噪处理
首先对回波信号y(t)进行采样处理,得到离散采样数据y[k],y[k]=c0,k,则信号y(t)的小波变换分解为:

其中cj,k为尺度系数,dj,k为小波系数;h、g 为一对正交滤波器组;j为分解层数;N 为离散采样点数。
再对分解得到的每个小波系数进行阈值处理,阈值取:

此处N 为样本序列长度,取N=40 001。
分别用双重指数型阈值函数、软阈值函数和硬阈值函数对分解的小波系数进行处理,双重指数型阈值函数的参数取α=7。
最后通过反变换公式

重构函数,得到去噪处理后的信号。
3.3.2 结果对比
图5为分别使用双重指数型阈值函数、“软阈值函数”和“硬阈值函数”三种阈值函数对信噪比为10 dB的回波信号作去噪处理后得到的信号放大到单个脉宽的信号图,从图中可看出,“软阈值函数”处理后的信号较双重指数型阈值函数和“硬阈值函数”处理后的信号更为平滑,但是在信号幅度上有明显的衰减,这对于通过回波信号的幅度大小判断目标方位的无线电定向探测引信的定向精度有很大影响。双重指数型阈值函数和“硬阈值函数”处理后的信号仅从图中无法看出明显区别,可以通过计算处理后信号的信噪比、与原始信号的均方差进行优劣判别。
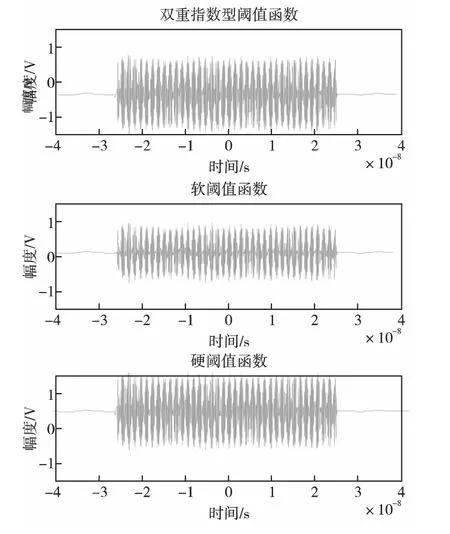
图5 回波信号去噪结果Fig.5 Echo signal denoising results
将原始信号y 作为标准信号,则经过小波去噪后的估计信号y'的信噪比(SNR)公式定义为:
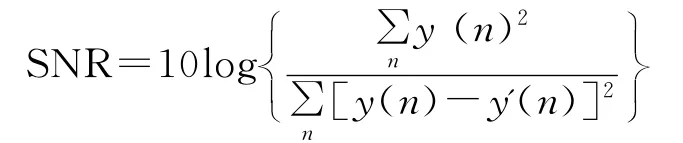
原始信号与估计信号的均方差(MSE)定义为:

上述两个公式中n为信号长度。
估计信号的信噪比越高,原始信号与估计信号的均方差越小,则估计信号越接近原始信号,去噪效果越好。表1中列出了使用双重指数型阈值函数、软阈值函数和硬阈值函数三种情况下,估计信号的信噪比和均方差的比较。从信噪比和均方差的角度看,使用双重指数型阈值函数去噪后得到的估计信号信噪比最大,与原始信号的均方差最小,去噪效果最好。
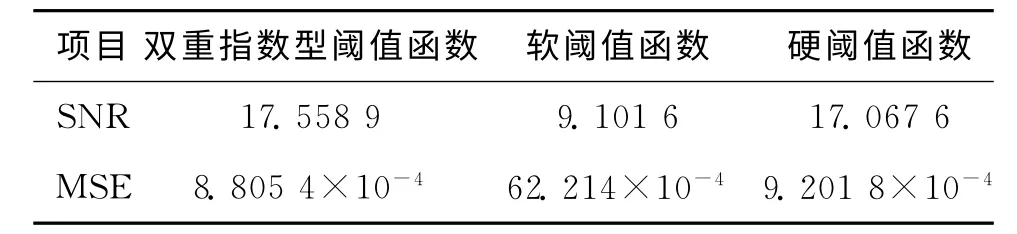
表1 三种去噪结果比较Tab.1 Result comparison of three kinds of de-noising
通过多次仿真验证发现,当回波信号信噪比为1dB时,使用双重指数型阈值函数对回波信号作去噪处理,处理后信号信噪比约为4.8dB;当回波信号信噪比为0dB时,使用双重指数型阈值函数对回波信号作去噪处理,处理后信号信噪比约为1.4 dB,此时信号与噪声的功率相差不大,去噪效果已经开始呈现不理想的状态;当回波信号信噪比为-1 dB时,处理后信号已出现明显丢失。具体结果如图6所示。

图6 处理不同信噪比的回波信号Fig.6 Process echo signal has different SNR
4 结论
本文提出双重指数型阈值函数对多普勒回波信号进行去噪处理。该阈值函数呈双重指数形式,不是分段函数,含有一个调控参数控制估计的小波系数向分解的小波系数或0逼近的速度,以阈值和分解的小波系数的比值是否大于1判定估计的小波系数逼近的方向。仿真结果表明使用双重指数型阈值函数去噪后得到的信号最为平滑。在回波信号信噪比低于0dB时,使用双重指数型阈值函数去噪效果不理想。在对多普勒回波的去噪过程中,使用双重指数型阈值函数去噪后得到的信号的信噪比大于使用“软阈值函数”和“硬阈值函数”得到的信号的信噪比;使用双重指数型阈值函数去噪后得到的信号与原始信号的均方差小于使用“软阈值函数”和“硬阈值函数”得到的信号与原始信号的均方差,双重指数型阈值函数在去噪效果上优于传统的“软阈值函数”和“硬阈值函数”。
[1]杨建国.小波分析及其工程应用[M].北京:机械工业出版社,2005.
[2]Delyon B,Juditsky A,Benverniste A.Accuracy Analysis for Wavelet Approximation[J].IEEE Transactions on Neural Networks,1995(6):320-350.
[3]Donoho DL,Johnstone I.Wavelet shrinkage:Asymptopia[J].Journal of Royal Statistical Society,1995,57(2):301-369.
[4]Gu Jie.Wavelet Threshold De-noising of Power QualitySignals[C]//Fifth International Conference on Natural Computation,2009(6):591-597
[5]K Berkner,Jr R O Wells.Wavelet transforms and denoising algorithm [C]//Signal,System & Computers,Conference Record of the Thirty-Second Asilomar Conference.Pacific Grove,California:Monterey Bay Aquurium Research Institute,1998:1639-1643.
[6]Donoho DL.De-noising by soft-thresholding[J].IEEE Trans.on Inf.Theory,1995,41(3):613-627.

