基于OFDM 信号分布的指数查询表索引算法

丛 犁，李晓记

(1.国家电网吉林省电力有限公司信息通信公司，长春130021;2.桂林电子科技大学广西无线宽带通信与信号处理重点实验室，广西桂林541004)

0 引 言

功率放大器(PA:Power Amplifier)将已调信号放大至所需功率，是现代无线通信系统中不可缺少的关键部件。但是，高功效PA本身具有很强的非线性特性，在非恒包络系统中会导致严重的非线性失真问题，这就造成现代通信系统中广泛应用的正交频分复用(OFDM:Orthogonal Frequency Division Multiplexing)调制信号受PA影响非常严重［1，2］。由于调制后的OFDM信号存在高峰均比(PAPR:Peak to Average Power Ratio)的固有缺点，造成PA较多运行在非线性工作区。所以，PA的非线性失真会导致两方面的问题:1)星座点扭曲造成误码率性能的下降;2)频谱的带外增生造成邻道信号干扰［3－5］。为了解决这一问题，人们提出了放大器的预失真线性化技术［6－10］，通过展宽放大器的线性区间，避免失真现象。其中查询表(LUT:Look－Up Table)预失真法由于实施效果好、实现简单，得到了广泛的应用。

传统的LUT方法在确定信号对应的地址索引时，采用的是均匀索引算法［4，5，11－14］，均匀索引算法为

其中m指输入信号幅度为Am时的索引地址;Asat是PA的饱和输入幅度，亦即允许放大信号幅度的最大值，与PA的饱和点相关;N是查询表的大小。这种均匀索引算法复杂度低，适应性和通用性强，但由于没有考虑输入信号的幅度分布特性，因此会带来如下几个问题:1)当信号幅度属于非均匀分布时，由于其不同幅度的信号出现概率并不相同，这就造成概率高的信号对应的LUT表项值更新频率高，出现概率低的信号对应的LUT表项值更新频率低，从而导致LUT更新频率不一致，进而影响系统性能;2)由于此时的索引精度仅与查询表的大小N相关，因此，提升精度依赖于N的提升，为了达到较高精度需要大容量的LUT，易造成硬件资源紧张。

为解决这一问题，人们陆续提出了多种改进的地址索引算法。文献［15］是较早开始研究该问题的文献之一，提出了基于PA放大特性的LUT地址索引算法，并在此基础上给出了适用于任何系统的一个优化索引算法;但在实际中PA的功放特性往往是无法精确得知的。文献［16］提出一种采用自适应方式调整查询表间距的方案，以满足不同系统下最优查询表索引的问题。但由于采用了自适应的方案，在一般情况下，文献［9］的方法只能给出最优解中一个较好的近似解，而无法达到最优解。将文献［9］提出方案推广后，文献［17］提出了分段内插的地址索引算法，同时提出了基于PA失真特性的最优LUT分段算法;但由于其针对通用系统，并未考虑到OFDM信号的具体特性，因此在OFDM系统中应用时，算法复杂度较高，其硬件实现成本高。实际上，目前的地址索引算法仍以简单的均匀索引算法为主。

为解决均匀索引算法在OFDM系统应用中存在的问题，在不明显增加复杂度的基础上，笔者提出一种新型的结合OFDM信号的统计分布特性的查询表指数地址索引算法。通过在地址索引算法中引入信号分布特性，使LUT表项值更新频率趋于一致，同时降低LUT表的容量，消除PA饱和点带来的影响，因此能有效解决上述问题。

1 背景原理

1.1 OFDM信号幅度分布特性

OFDM信号是多个子载波的叠加信号，当子载波足够多时，根据中心极限定律，OFDM信号的正交分量和同相分量均为高斯信号，OFDM信号的幅度服从瑞利分布，而相位服从均匀分布(见图1)。依据上述结论，可以直接得到OFDM样点幅度的概率密度函数

式(2)中，r为输入信号的幅度，2σ2是输入信号的平均功率，在本文中用功率符号Pav代表，因此Pav=2σ2。由图1可以看出，OFDM信号幅度分布特性是大幅度信号和小幅度信号的出现频率较低，中等幅度信号的出现频率较高。

1.2 功率回退情况下OFDM信号幅度分布特性

对于OFDM信号，由于其存在PAPR高的固有缺点，PA会对其造成严重的非线性失真。为了消除这种非线性失真，必须将PA的输入信号进行功率回退，将大部分输入信号缩小至线性放大区。PA功率回退

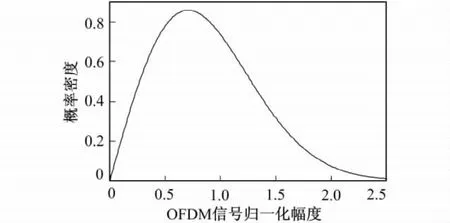
图1 OFDM信号幅度分布曲线Fig.1 OFDM signal amplitude distribution curve

一般采用输入功率回退(IBO:Input Back－Off)进行衡量，可定义为

其中Psat为功放的饱和输入功率，Pav为回退后信号的平均功率。一般而言，对于采用16QAM方形映射256子载波的OFDM系统，其输入功率回退通常接近8 dB。

功率回退会降低待传输的已调OFDM信号的平均功率，即降低PA的输出信号平均功率，因而IBO的存在严重影响了PA的功率效率;另一方面，如果单方面减小IBO，又会导致信号较多，超出PA饱和区域，造成失真更为严重。为了解决这一矛盾，研究存在IBO情况下的索引算法很有必要。在考虑IBO的影响的情况下，OFDM信号的平均功率发生了改变，即平均功率

2 新型指数地址索引算法

2.1 LUT的等概率分布下标

查表法在本质上是将信号分成若干段，利用分段信号逼近原始信号;当分段数目趋近于无穷时，分段信号等价于原始信号。因此，在LUT中常用分段结束位置的下标表示对应幅度信号的地址索引(见图2)，图2中tm表示［tm－1，tm］分段的结束位置，m为其下标;当信号幅度Am∈［tm－1，tm］时，其对应的索引地址为m。

图2 LUT位置及下标示意图Fig.2 Location and subscript of LUT

均匀索引算法中，所有分段的长度是相等的，但在信号幅度分布特性不均匀的OFDM系统中，会造成每个小区间分布信号概率不同，从而引发查询表更新不同步。因此，对于OFDM信号，为使所有LUT表项值更新频率相等，必须使LUT表项对应的范围［ti，ti+1］和［tj，tj+1］(i≠j)内出现的信号概率相等。由于此时的索引依据是信号幅度，因此t必须满足

其中N为查询表容量。式(5)可采用数学归纳法求解t的结果，过程如下。

1)当m=1时，式(5)简化为

一般情况，取t0=0。将式(2)带入式(6)并求解，可得

最终求得

2)当m=k时，依据式(9)，设

成立，则当m=k+1时，式(5)变为

将式(10)带入式(11)并化简后可得

因此，综合1)和2)，可证得

2.2 确定地址索引公式

当输入信号的幅度为Am时，通常会使用Am所处区间的结束位置tm的下标m定位信号。因此

对式(14)求解可得

式(15)给出了基于OFDM信号幅度分布特性的地址索引算法的表达式，由于其表示为一个exp()函数形式，因此称之为指数索引算法。图3给出了指数索引算法与均匀索引算法的对比图(横坐标为归一化的信号幅度)。

由图3可见，均匀索引方法的表项间距是均匀的，而指数索引方法的表项间距分布是非均匀的。正是这种非均匀性，使指数索引算法中大信号区域和小信号区域的表项间距较宽，属于这些区域的信号出现概率相比均匀索引增大;而中等信号区域表项间距变小，使信号出现频率相比均匀索引有所降低，从而各个表项区间信号出现频率一致，最终达到表项值更新频率一致的目的。

图3 线性查询与指数查询表间距分布示意图Fig.3 Distance distribution of linear and exponential lookup table

当系统存在功率回退时，由式(4)可知

此时，式(15)可改写成

式(17)给出了存在功率回退情况下的指数索引算法公式。由式(17)可知，指数索引算法与IBO密切相关，因此查询地址能更真实地反应信号幅度信息，最终达到提升在小IBO情况下的系统误码率性能、同时降低查询表容量的目的。

另一方面，对于硬件实现，式(17)中使用输入信号的功率代替幅度计算地址索引值;由于硬件实现中的幅度信息实际由功率信息开方得到，因此，采用指数索引算法减少一个开方运算，有利于节约硬件资源;同时，在复杂度方面，由于exp()函数的求解可以利用查表法实现，所以，相比均匀索引算法复杂度提升不高。

3 仿真结果

笔者利用Matlab仿真工具验证结论。仿真系统采用512子载波的OFDM调制系统，同时采用功率归一化的16QAM方形映射。PA采用在仿真中广泛应用的Saleh模型

其中f(A)和g(A)分别表示PA的AM－AM幅度失真和AM－PM相位失真。而预失真技术采用RASCAL算法予以实现。

3.1 IBO较小时的系统性能

IBO与输入功放信号幅度有直接关系，当IBO较大时，输入信号幅度变小，功放线性放大性能变好，但严重降低了功放效率，大量的能源以热能的形式被消耗。由于IBO的减小能直接提升放大效率，节约能源，因此，研究IBO较小情况下的系统性能十分重要。图4显示了在不同的IBO条件下，线性查询算法和指数查询算法的误码率性能。

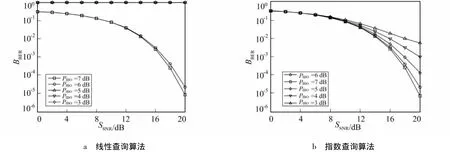
图4 不同IBO条件下误码率性能Fig.4 Different IBO condition algorithmunder

从图4可以看出，当PIBO≤5 dB时，线性查询算法误码率性能急剧恶化，起不到消除功放失真的作用;当PIBO＞5 dB时，线性查询算法的误码率性能会有明显提升，并且随着IBO的增大和功放线性放大性能的提升而越来越好，这意味着对于线性查询算法，存在一个IBO阈值，只有满足阈值条件的IBO才能实现预失真的功能。对于指数查询算法，在低于阈值的IBO环境中，其误码率性能相比线性查询算法有明显提升，而在超过阈值的IBO环境中，其误码率性能基本与线性查询算法保持一致。因此，指数查询算法性能不存在工作阈值，并且能在小IBO环境中保持较好的误码率性能，能有效改善功放的放大效率。

3.2 系统性能损耗

功放的IBO越大，PA的非线性失真影响越小，当IBO增大到一定程度时，PA的非线性失真基本可以忽略不计，但IBO的增大也伴随着PA放大效率的不断降低;另一方面，发射端往往需要增大发射功率，以提高信号的信噪比性能，这等同于系统增加了损耗，降低了系统的整体效率。因此，笔者引入系统性能总损耗(TD:Total Defense)，表示特定的BER性能下系统性能与功放IBO的关系，定义为

其中SHPA是当输入信号通过包含PA的高斯白噪声信道时，为了达到给定的BER所需的信噪比;而Sawgn表示输入信号仅通过高斯白噪声信道时，为了达到给定的BER所需的信噪比。在BBER=10－3的情况下，指数查询算法和线性查询算法的TD比较结果如图5所示。

图5 TD性能比较Fig.5 Comparison of TD characteristic

由图5可以看出，当IBO较小时，指数查询算法性能较线性查询算法下降明显，其TD性能降低较多;IBO超过4 dB后，线性查询算法的性能得以提升。

4 结 语

当前，通信网络的大能耗问题极大制约了通信技术的发展。为了降低通信网络能耗，笔者围绕预失真技术中的一个关键技术 查询表地址查询算法进行研究，目的在于解决OFDM系统中应用线性查询预失真算法导致的查询表表项值更新不一致问题。笔者基于OFDM信号幅度的分布规律，提出了一种新型的指数型查询表索引方法。通过与已有算法进行比较，指数查询算法不存在工作阈值，在小IBO条件下依然能维持较好的误码率性能，能显著改善功放的功率效率，提升功放回退较小情况下的系统性能;同时，在不降低误码率的前提下，指数查询算法所需的查询表容量更小，因此，能简化物理实现时的硬件复杂度，具有较好的性能。

［1］WANG T，ILOW J.Compensation of Nonlinear Distortions with Memory Effects in OFDM Transmitters［C］∥IEEE Global Telecommunication Conference.Dallas，USA:IEEE，2004:2398－2403.

［2］SHI Zhan，ZHOU Jianmin，LI Hui，et al.Performance Analysis for Scalar Digital Predistortion［C］∥Radio and Wireless Symposium(RWS).Austin，TX，USA:IEEE，2013:88－90.

［3］CRIPPS S.RF Power Amplifiers for Wireless Communications［M］.Boston:Artech House，2006:35－43.

［4］REN Zhiyuan，LI Yongzhao，ZHANG Hailin，et al.A High Power Efficiency Method Using Orthogonal Signal Decomposition in High PAPR System ［J］.Science China－Information Sciences，2013，56(4):404－410.

［5］REN Zhiyuan，ZHANG Hailin.A Novel Distortion Elimination Method of Power Amplifier in Wideband OFDM System ［J］.Science China－Information Sciences，2012，55(2):396－406.

［6］ROGER F.A 200 mW 100 MHz－to－4 GHz 11th－Order Complex Analog Memory Polynomial Predistorter for Wireless Infrastructure RF Amplifiers［C］∥ Solid－State Circuits Conference Digest of Technical Papers(ISSCC).2013 IEEE International.San Francisco，CA，USA:IEEE，2013:94，95，17－21.

［7］KWAN A K，BASSAM S A，HELAOUI M，et al.Concurrent Dual Band Digital Predistortion Using Look Up Tables with Variable Depths［C］∥Power Amplifiers for Wireless and Radio Applications(PAWR).2013 IEEE Topical Conference on.Santa Clara，CA:IEEE，2013:25，27，20－20.

［8］HAMMI O，KWAN A，GHANNOUCHI F M.Bandwidth and Power Scalable Digital Predistorter for Compensating Dynamic Distortions in RF Power Amplifiers［J］.Broadcasting，IEEE Transactions on，2013，59(3):520－527.

［9］CHEN S，HONG X，GONG Y，et al.Digital Predistorter Design Using B－Spline Neural Network and Inverse of De Boor Algorithm［J］.Circuits and Systems Ⅰ:Regular Papers，IEEE Transactions on，2013，60(6):1584－1594.

［10］SHI Zhan，LI Hui，ZHOU Jianmin，et al.Time Domain Delay Items Design for Memory Orthogonal Polynomial Predistorter［C］∥Vehicular Technology Conference(VTC Spring).2012 IEEE 75th.Yokohama，Japan:IEEE，2012:1，5，6－9.

［11］JARDIN P，BAUDOIN G.Filter Lookup Table Method for Power Amplifier Linearization［J］.IEEE Transactions on Vehicular Technology，2007，56(3):1076－1087.

［12］KATHLEEN J M，MOHSEN KAVEHRAD，RAJEEV KRISHNAMOORTHY.Look－Up Table Techniques for Adaptive Digital Predistortion:A Development and Comparison ［J］.IEEE Transactions on Vehicular Technology，2000，49(5):1995－2002.

［13］WRIGHT A S，DURTLER W G.Experimental Performance of an Adaptivedigital Linearized Power Amplifier［J］.IEEE Trans on Vehicular Technology，1992，41(4):395－400.

［14］CAVERS J K.Amplifier Linearization Using a Digital Predistorter with Fast Adaptation and Low Memory Requirements［J］.IEEE Transactions on Vehicular Technology，1990，39(4):374－382.

［15］CAVERS J K.Optimum Table Spacing in Predistorting Amplifier Linearizers ［J］.IEEE Transactions on Vehicular Technology，1999，48(5):1699－1705.

［16］BA S N，WAHEED K，ZHOU G T.Optimal Spacing for a Polar Look－Up Table Predistorter［C］∥2007 International IEEE Northeast Workshop on Circuits and Systems(NEWCAS'07).Montreal:IEEE，2007:189－192.

［17］BA S N，WAHEED K，ZHOU G T.Optimal Spacing of a Linearly Gain LUT Predistorter［J］.IEEE Transactions on Vehicular Technology，2010，59(2):673－681.