马氏体相变研究的最新进展(六)

刘宗昌，计云萍

(内蒙古科技大学材料与冶金学院，内蒙古包头 014010)

5 马氏体相变的切变机制及其误区

1924年Bain提出了马氏体相变机制的第一个模型，为压缩应变模型。1930年提出第1个切变模型，在以后的40余年中提出了一系列切变模型，由于每个模型均难以与实际符合，不断修改或“完善”，到70年代共提出了8个晶体学切变模型。但最终所有的切变模型均与实际不符。马氏体相变的形核长大、马氏体形貌、缠结位错、精细孪晶、微细层错、位向关系、表面浮凸等试验现象均不能用切变机制作出明晰而合理的解释。晶格切变耗能太大，相变驱动力无力克服切变应变能。马氏体相变的切变学说无论实践检验还是理论检验都是不合格的，因此马氏体相变的切变“理论”尚不能称为理论，而是不完整、不成熟的学说。

造成切变学说误区的原因之一是没有采用系统科学的方法进行研究。在20世纪，材料科学家首先研究了珠光体转变机理，紧接着就进行了马氏体相变机理的研究，因为珠光体组织和马氏体组织发现最早。学者们分别孤立地进行了共析分解机理和马氏体切变机理的研究。而贝氏体组织的发现较晚(约晚60年)，20世纪50年代，贝氏体相变机制开拓者则借用了马氏体的切变机制来解释贝氏体的成因。20世纪70年代，扩散学派利用共析分解理论解释贝氏体相变。他们都忽视了贝氏体相变的过渡性，都没有把过冷奥氏体转变作为一个整合系统来研究，忽略了共析分解、贝氏体相变、马氏体相变三者的相关性、过渡性、交叉性，孤立地进行了马氏体相变切变机制的研究。

20世纪前半叶，材料研究设备仪器落后，而SEM、TEM、HRTEM、STM等均是20世纪后半叶才投入应用的，因此对马氏体相变和马氏体的物理本质缺乏深入细致的试验观察，所提出的切变机制缺乏充分的试验依据，造成理论上的重重误区。

5.1 马氏体相变切变机制的研究历程及评价

过冷奥氏体的转变是一个整合系统，应当将共析分解、贝氏体相变、马氏体转变作为一个整体，运用系统科学的方法进行研究。但历史上，贝氏体组织的发现晚于马氏体组织近60年，也即人类对马氏体相变的研究早于贝氏体相变约半个世纪，因此，马氏体相变的研究一直处于“孤立”的状态，缺乏与中温转变的联系，不能从贝氏体相变研究中获得启发。相反，20世纪50年代提出的贝氏体相变机制，却借用了马氏体相变的尚不成熟的研究结果，指出贝氏体相变具有马氏体相变那样的切变机制。

70年代，美国学者Aaronson从能量上否定了切变学说，指出贝氏体就是共析分解的产物，认为贝氏体相变具有共析分解那样的扩散机制［30］。从而导致了贝氏体相变形成两个学派，即切变学派和扩散学派，并且两派进行了近40年的学术论争。就这样，马氏体相变机制的研究一直没有纳入过冷奥氏体整合系统，而“孤军奋战”到20世纪末。使学术界误认为切变机制是成熟的理论，至今，切变学说仍然被一些学者“奉为至宝”。

刘宗昌等人运用系统科学的方法，吸收了国内外学者正确的研究成果，同时指出了两派的错误观点，指出贝氏体相变既非切变过程，也非共析分解;并提出了贝氏体相变新机制，实现了贝氏体相变理论的整合［33］。贝氏体相变研究的新进展为马氏体相变的研究提供了新思路，促进了马氏体相变机制的研究。

马氏体相变机制与中温区的贝氏体相变存在密切的联系，它是过冷奥氏体从中温区到低温区，相变过程逐渐演化的结果。研究马氏体相变机制不能割裂与贝氏体相变的联系。

1878年，索拜Sorby首先用金相显微镜观察到淬火高碳钢中的硬相，即高碳马氏体组织。

1895年法国学者Osmond将钢中的这种硬相命名为马氏体(Martensite)。

1924年，美国学者Edgar Bain提出马氏体相变具有表面浮凸现象。并且提出了马氏体相变的应变模型，称为贝茵模型。

1926～1927年，W.L.Fink和 Γ.Β.库尔久莫夫等人各自分别用X-射线技术测得钢中马氏体为体心正方结构，并且第一次指出马氏体是碳在α-Fe中的过饱和固溶体。此发现在当时具有理论意义，此定义一直延续到20世纪末才有人提出修改意见。人们发现不仅钢中存在马氏体相变，而且在有色金属及合金，陶瓷材料中都可发生马氏体相变。故该定义过时。

1929年，周志宏等首先将电解铁淬入水银，获得马氏体组织。此举证明，马氏体也可以是体心立方结构，不为碳所过饱和。

1930年，Γ.Β.库尔久莫夫和 G.萨克斯(Sacks)首先测得1.4%C钢中马氏体与母相奥氏体保持一定的晶体学位向关系，即K-S关系［34］。据此设计了K-S切变模型，从此开始了马氏体相变切变机制、相变晶体学的研究。

1933年，R.E.迈尔(Mehl)测得中、高碳钢中马氏体在奥氏体的{225}γ晶面上形成，称其为惯习面［35］。

1934年，西山测得Fe-Ni合金马氏体相变时存在西山关系，并且设计了西山模型。它具有K-S模型同类的缺点。

1 949年，Greniger和Troiano测定了Fe-22%Ni-0.8%C合金中的马氏体位向，发现了G-T关系［36］。并提出马氏体相变是无扩散的切变过程。该模型力图解释位错和孪晶的存在和表面浮凸的形成。

1951年，J.W.Christian首先提出了马氏体相变的层错形核模型［37］。

1953年，Frank首先提出Fe-C{225}γ马氏体与母相间的位错界面模型。促成了K-D位错胞核胚模型的提出。但K-D位错胞马氏体核胚模型至今没有得到试验证实。母相和马氏体中均不可能存在如此高的位错密度，理论上与实际不符。

1953～1954年，由 M.S.Wechsler等(W-L-R)和J.S.Bowles等(B-M)分别独立地提出两个马氏体相变的表象学假说，其一称为“W-L-R理论”;另一个称为“B-M 理论”［38－39］。两者基本上等价，即指两者的出发点和推理过程相近。学术界称其为出色的“表象学理论”，现在从试验和理论上分析，这两个学说的物理模型是错误的，因此其计算结果与实际不符是必然的，虽然个别合金中计算结果与实际符合，但计算机算出的结果是个案，不可信。

马氏体相变表象学说将贝茵应变B，形状应变F，简单切变S和刚性转动R，用一个矩阵式描述:即F=RBS。此计算式的物理模型不正确，其中:

1)贝茵应变B太大，达21%，这与实际不符;

2)形状应变F，用浮凸值表示，浮凸是相变比体积变化所致，是一级相变的必然结果，并非切变过程。

3)简单切变S，不能获得真正的马氏体晶格参数，并且耗能太大。

4)刚性转动R是虚拟的，实际上不存在。

物理模型的不当，必导致计算结果与实际不符，虽然在Au-Cd等合金中得到证实，但仅是个案，不具普适性。对于低碳钢、中碳钢、高碳钢马氏体的计算结果与实际均不符。针对Fe基马氏体，在20世纪70年代提出了非均匀切变模型，即所谓“近代唯象理论”。该假说较原始表象学说作了更多的假设，处理更复杂，但是在定量计算上仍然无能为力［37］。

1964年，Bogers-Burgers双切变模型被提出。

60年代末，70年代初，先后提出马氏体相变的协作形变“理论”和范性协作模型，以及多次切变模型。到20世纪末就马氏体相变机制已经提出8种切变模型，但均不够成熟。

总之，19世纪末到20世纪前叶，学者们分别孤立地进行了珠光体转变、马氏体相变和贝氏体相变的研究，虽然取得了一定的成果;但不足之处是没有把过冷奥氏体作为一个整合系统来研究，理论研究缺乏系统性，整体性，忽略了共析分解、贝氏体相变、马氏体相变三者之间的内在联系。在没有应用先进设备搞清其物理本质的情况下，过早地确定其转变机制，因而出现认识上的偏差和错误在所难免。

直到20世纪末，马氏体相变切变机制的研究也没有形成完整而成熟的理论体系，假说多，模型多，与实际相差甚远。

5.2 马氏体相变晶体学的经典模型

相变晶体学是相变机制的核心内容，如果说相变热力学、动力学的研究是外围战，那么，晶体学的研究则是攻坚战。一个世纪以来，马氏体相变晶体学研究进行了大量理论研究工作，提出许多模型或假说。

20世纪对马氏体相变晶体学的研究经历了三个阶段:

第一阶段，1924年Bain提出了应变模型。该模型不能说明惯习面，而且应变太大，不能说明马氏体的亚结构等，故为人们所摈弃。

第二阶段，从1930年开始，提出了一系列晶格切变模型，如K-S模型、西山模型、G-T模型、B-B双切变模型、藤田模型等。这些模型均为针对某一具体发现的事例，设计一种切变模型，以说明相变时原子的具体移动方式，说明位向关系、惯习面等。但是，这些切变模型均不能与实际完好地吻合。

第三阶段，50年代初，提出了马氏体相变晶体学唯象学说。晶体学唯象学说只推测相变过程的表象，而不能描述原子的迁动过程。它吸收了贝茵应变模型和切变模型的成分，从“不变平面应变”这一个基本观点出发，设计了一套可以定量计算的应变模型。力图说明母相、新相的点阵结构、位向关系、惯习面(指数)、外形变化、亚结构之间的关系，但多与实际不符。

上述三个阶段中，形成了许多个模型或假说，科学技术哲学告诉我们，假说只有不断地被证实，才能上升为理论。因此切变机制尚不是成熟的理论。以下仅介绍几种经典的切变模型。

5.2.1 K-S切变模型和西山模型

5.2.1.1 K-S 切变模型

20世纪30年代初，库氏和Sachs确定了1.4%C钢中奥氏体与马氏体之间的位向关系为:

{111}A//{011}M＜110＞A//＜111＞M此称为K-S关系。据此设计了材料学界众所周知的K-S晶格切变模型。

根据K-S关系，新相和旧相晶体的密排原子面相互平行，认为相变时，母相的{111}γ面将转变为新相的{011}α面。因此，首先需要弄清{111}γ和{011}α面的原子排列情况和堆垛次序。见图63，底面为密排面{111}γ。堆垛次序为ABCABCAB……，●表示底层原子A，⊕表示中间层(第二层)原子B，○表示顶层(第三层)原子C。

图64(a)是1.4%的Fe-C马氏体的原子排列情况和堆垛次序，为体心正方结构(bct)，底面为{011}α。图64(b)图是体心立方结构的α-Fe的原子排列情况和堆垛次序，底面也为{011}α。

切变分三步进行:

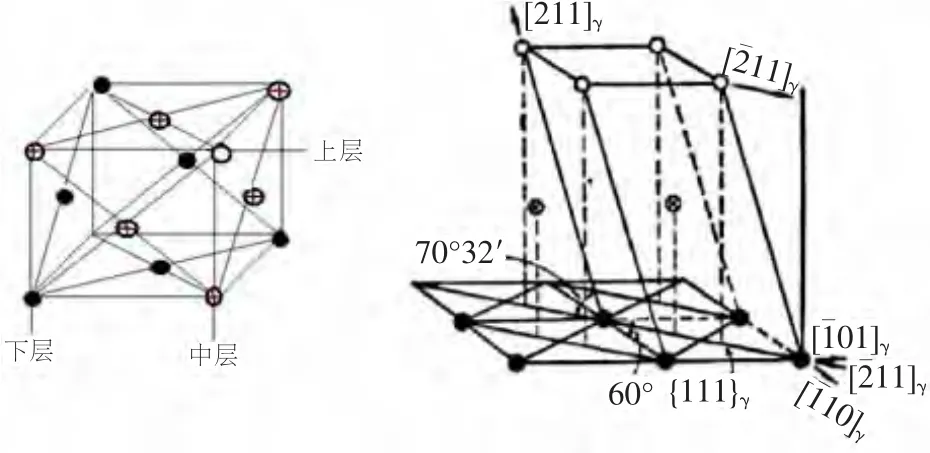
图63 {111}γ面原子堆垛Fig.63 Atomic stacking of{111}γ

图64 (a)体心正方马氏体和(b)体心立方α-Fe原子堆垛Fig.64 Atomic stacking of(a)body-centered tetragonal Martensite and(b)body-centered cubic α-Fe

1)第一切变:见图65，底面为{111}γ菱形，菱形角为60°。切变在{111}γ面上，沿着［11］γ方向进行，底层原子不动，第二层⊗原子沿［211］γ方向移动0．057nm，○层原子移动0．114nm，切变角为19°28';含碳 1．4% 的 Fe-C 马氏体(c/a=1．06，下同)，切变角则为 15°15'。

2)第二切变:在{211}α面上，沿着［111］α方向进行一次小的切变，使60°角变成69°。如果不含碳，则使 60°角变成 70°32'，如图 66 所示。

3)第3步，晶格线性调整，为使其符合实际的马氏体晶格的面间距等参数，转变为bccM(0%C)，进行晶格参数调整，晶格参数调整量列于表3中。

各切变参数依下列各式计算:

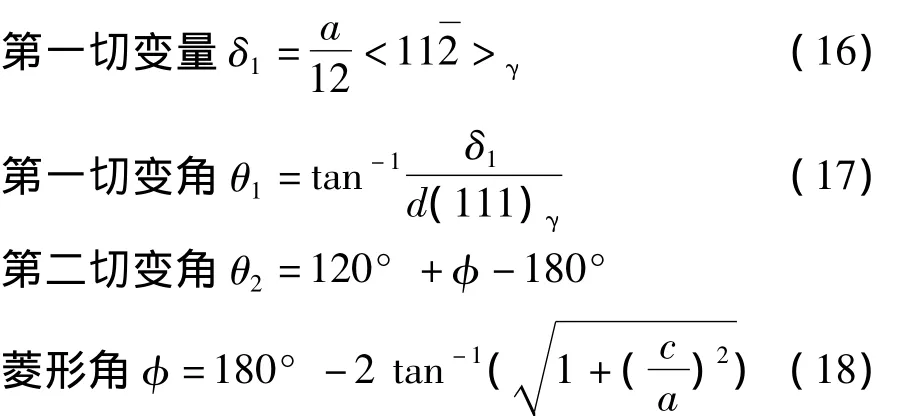
许多书中将上述过程集中描绘在一个图中，即将原子的迁移情况投影在底面菱形上，来表示切变全过程，图67为K-S切变模型的平面投影［6］。图67(a)表示{111}γ上原子的排列情况，图67(b)表示第一切变后的情况，图67(c)表示第二切变后的情况，图67(d)表示经调整成c/a=1.06的体心正方结构，图67(e)表示经过调整成体心立方 α-Fe的{011}α面上的原子排列情况。

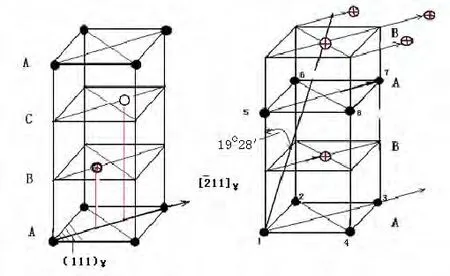
图65 K-S第一切变Fig.65 The first shear of K-S

图66 K-S第二切变Fig.66 The second shear of K-S

表1 γfcc→αbcc时主要晶格参数变化Table 1 The changes of main parameter of crystal lattice at γfcc→αbcc

5.2.1.2 西山切变模型

1934年，西山善次研究了Fe-Ni(34% ～37%Ni)合金的马氏体相变，发现西山关系。并且提出一个切变模型，被称为西山模型。此模型的第一次切变与K-S模型相同，也是在{111}γ晶面上，沿着［211］γ方向切变19°28'。但随后不进行K-S模型的第二次切变，而是直接进行晶格参数调整，如使［211］γ轴收缩7.5%，［111］γ轴收缩1.9%，［110］γ轴膨胀13.3%，再使底面内角由60°调整到70°32'。经过这些调整，使其与实际的马氏体晶格相符。西山关系与 K-S 关系相差 5°16'［6］。

图67 K-S切变模型的平面投影Fig.67 The plane projection of K-S shear model

5.2.1.3 K-S 模型和西山模型的误区

两个模型通过晶格切变，力图得到了体心立方结构的马氏体，但问题较多:

1)惯习面不符合。按此模型，惯习面应为{111}γ，而实际上 Fe-C合金马氏体的惯习面有{557}γ、{225}γ、{259}γ;具有西山关系的 Fe-Ni(34% ～37%Ni)合金，其惯习面是{259}γ，而非{111}γ。

2)不能解释马氏体中孪晶、位错、层错等亚结构的形成，也不能解释浮凸现象。

3)不符合省能原则。该模型的第一、第二两次切变，是单晶体的晶格切变(当时还没有发现位错、孪晶缺陷)这种晶格切变消耗的切变能太大，相变驱动力不足以完成切变过程［40］。

4)按照K-S模型和西山模型，第一切变后，并没有改变晶格类型，如切变前的堆垛方式是ABCABCABC…….，切变后变为ABABAB………，相当于抽出了C层。而A层、B层上的原子排列仍然与母相fcc上的A层、B层相同。即按照塑性变形理论，单纯的切应变是不能改变晶格类型的。

5)按照K-S模型，第一、第二两次切变后并没有得到实际的马氏体晶格，还需要调整晶格参数。西山模型的切变与K-S模型的第一切变相同，但不进行第二切变，然后进行晶格参数调整。晶格参数的调整需要原子再位移，怎么位移?位移就要再耗能。这些模型均没有考虑。

6)设想若省略第一切变、第二切变，直接进行晶格参数调整，将所有晶格参数均调整为马氏体的晶格参数，就实现了晶格重构，变成了马氏体。何必要切变呢?而且切变耗能太大，热力学上不可能实现。

即使按照切变学说发生了晶格切变过程，切变也没有得到符合实际的真正的马氏体晶格参数。按照金属学原理，塑性变形不能改变晶格类型，因此这些模型均指出还需要晶格参数调整。奥氏体转变为马氏体本来就是晶格重构的过程，就是晶格参数调整的过程。因此切变是多余的动作，是臆造出来的。

面心立方的母相转变为体心立方的马氏体相，就是晶格重构的过程，即晶格参数调整的过程。这种调整是母相原子向新相热激活迁移过程，是新旧相自由焓差作用下的自发过程。切变徒劳无功，反而消耗了巨大的切变能。因此切变模型不可取。

5.2.2 马氏体相变的G-T模型

G-T模型也是一个具有代表性的经典模型。在1 949年A.B.Greninger和A.R.Troiano测得了Fe-22Ni-0.8C合金单相奥氏体转变为马氏体，惯习面为{259}γ，其位向关系接近K-S关系，称为G-T关系，实际上是偏离K-S关系1°～2°，即:

{110}α'//{111}γ差1°

＜111＞α'//＜110＞γ差2°

据此G-T关系，他们以均匀切变和非均匀切变合成的方式，提出了G-T模型。指出可以在主切变的基础上沿着“马氏体”一定的晶面进行第二次切变。沿着惯习面的第一次切变为主切变，是均匀切变，而第二次切变是非均匀切变。如图68所示。

物体的应变分为均匀应变和非均匀应变两类。均匀应变是指系统内每一个基本单元，如每个晶胞发生的应变量等于宏观应变量。如热膨胀即是常见的均匀应变。从晶格的角度讲，均匀应变总是晶格类型的改变或晶格参数的变化。非均匀应变就是系统内各部分应变量不同，如金属的塑性变形在微观上是不均匀的。

图6 8(a)均匀切变和(b)非均匀切变Fig.68 (a)homogeneous shear and(b)non homogeneous shear

从图68可见，为了获得宏观切变角θ，可以采用均匀切变的方式，也可以采用非均匀切变的方式。非均匀切变可以通过δ和s的调整，采用滑移的方式或孪生的方式均可以达到目的。但δ值要比晶格常数大得多时，非均匀应变不改变晶格类型及参数。

图69是G-T模型的示意图，其中图69(a)表示以惯习面(中脊面)为基准的均匀切变，即主切变。图69(b)表示二次切变(滑移)的发生面，以及切变后外形的变化。二次切变是在经过主切变的“马氏体”中沿着{211}α晶面，在［111］α方向反复地进行滑移。

图69 G-T模型示意图Fig.69 Sketch map of G-T model

按照G-T模型，当非均匀切变区间距(δ)小于一定数值时，配以适当的切变量(s)，二次切变发生宏观为θ的切变。如果从图69的K方向看去，二次切变的情形如图70所示，θ为12°～13°，δ有十几个原子层厚。

(a)滑移;(b)孪生图70 二次切变(a)sliding;(b)hemitropism Fig.70 The secondary shear

完成G-T模型两次切变后，并没有完全达到实际马氏体晶体的要求，为了与实际的马氏体晶体相符，尚需作晶格参数调整。

G-T模型存在的问题是:

1)与惯习面不符，如该合金的惯习面实际是(225)γ，而非(259)γ。与小于1.4%C 的钢中马氏体的惯习面也不相符。

2)虽然预示马氏体中出现位错和孪晶，但是马氏体中的孪晶是相变孪晶，不是形变孪晶;是相变位错，不是形变位错。因此该模型不能解释马氏体中复杂的缠结位错、精细孪晶、层错形成的实际成因。也不能解释钢中马氏体的正方度。

3)两次切变没有得到真正的马氏体晶格，切变后仍然需要晶格参数调整，需要原子的再移动。

4)切变能量消耗太大，缺乏热力学可能性。

G-T模型的切应变动作是晶体在外力作用下的滑移和孪生，金属塑性变形不能改变晶格类型，因此将塑性变形的滑移和孪生应用于相变过程是不妥当的，马氏体中的位错和孪晶是相变过程中形成的，是相变位错和相变孪晶，不是形变造成的，二者不能混淆。

G-T模型完成两次切变消耗了巨大的切变能。遗憾的是切变后并没有得到实际的马氏体晶格，仍需进行晶格参数调整，才能与实际的马氏体晶格参数相同。这实际上是需原子再移动，再耗能，在已经消耗切变能量基础上还需要追加晶格参数调整的能耗。

总之，G-T模型沿袭了K-S、西山模型同样的错误，因此也是不可取的。

值得注意的是:Ti-5Mo合金中，成分与结构相同的母相形成的α马氏体，为六方结构，惯习面接近{344}β，但是没有亚结构，无亚结构的马氏体虽然少见，但也是马氏体相变。没有位错，也没有孪晶，还需要按G-T模型进行切变吗?还需要滑移或孪生吗?更应当注意的是:至今研究发现，不仅在有色金属的马氏体中存在层错亚结构，在低碳钢、高碳钢、铁基合金马氏体中普遍存在层错亚结构，而层错马氏体的形成不能用位错滑移或孪生等切变机制解释。可见切变模型是与实际马氏体相变无关的学说，是错误的。