构建物理模型 表露已知条件 求解物理问题＊

赵诗华 朱 琴 杨吉旺 张 飞

（1.中国矿业大学（北京）理学院，北京 100083；2.北京市昌平第二中学，北京 102208）

有不少物理问题，貌似已知条件不够，实际上只需要通过构建物理模型（或者物理过程），表露出已知条件，就能求解相关物理问题.

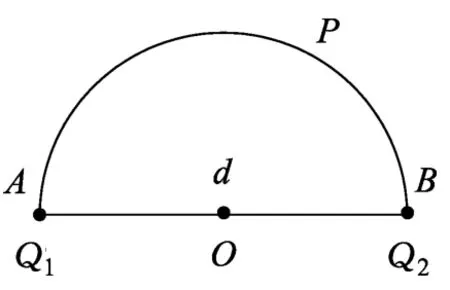
图1

例1.正点电荷Q1和Q2分别置于A、B两点，Q1＝Q，Q2＝4Q，相距为d，现以d为直径作半圆，如图1所示.试求在此半圆上电势最低点P的位置（用∠PAB表示）.

解析：对带电的质点，根据功能关系，仅电场力做功条件下，其动能Ek，电势能Ep电相互转化，总量守恒，即Ek＋Ep电＝恒量，所以动能最大处，对应电势能最小，电势能最小处，即为电势最低点.因此求解此题需构建一个只有电场力做功的物理模型.

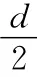
图2

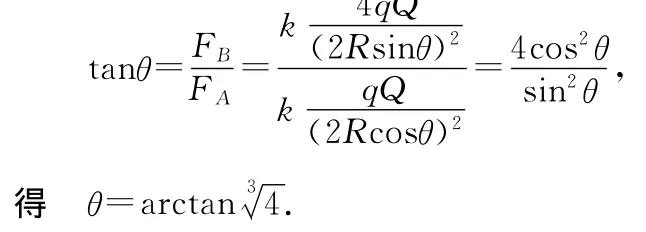
例2.如图3，椭圆半长轴为a，半短轴为b，焦距为2c，求4个顶点A、B、C、D的曲率半径.

解析：本题可以通过数学方法和物理方法求解.数学方法是，由椭圆方程对x求一阶导数和二阶导数，然后代入到曲率圆半径公式中即可求得曲率半径.物理方法是构建一个物理模型运用已知物理规律求解.

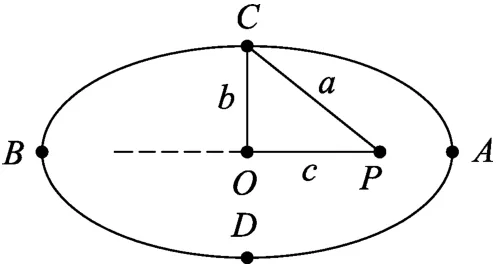
图3

该题可以建立地球绕太阳椭圆轨道运动的物理过程来求解.设地球质量为m，太阳质量为M位于焦点P点，设地球位于椭圆轨道的A、B、C点速度为vA、vB、vC，如图4.地球在A点时，由牛顿第二定律得

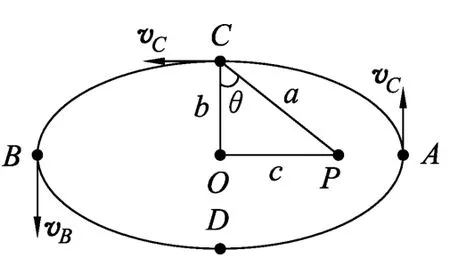
图4

由机械能守恒定律得

由开普勒第二定律得

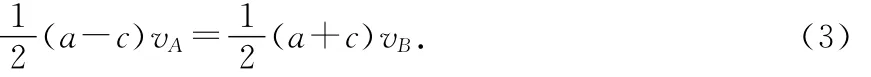
联列（1）～（3）式得

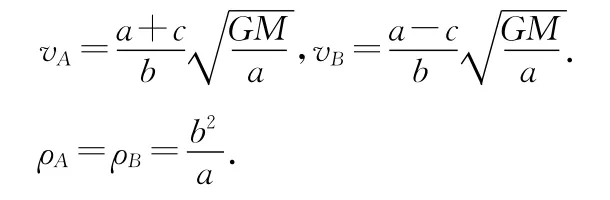
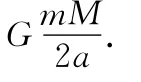
地球在C点时，由牛顿第二定律得

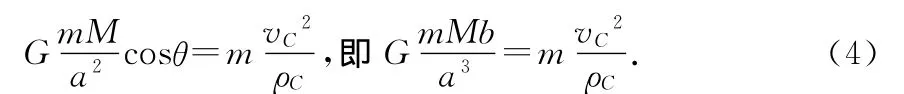
由机械能守恒定律得

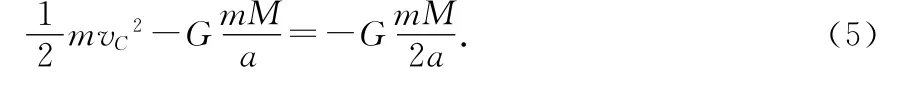
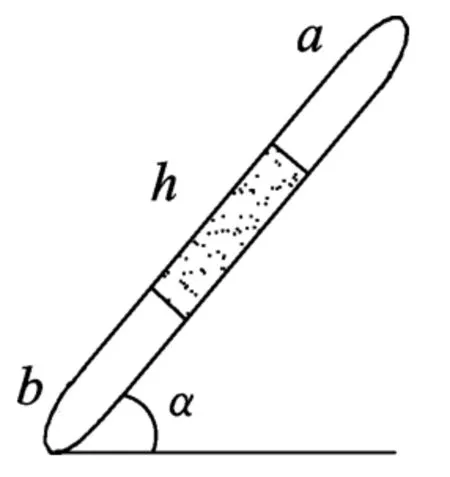
图5

例3.两端封闭的玻璃管内，有一段水银柱将管内气体分为两部分，玻璃管与水平面成α角，如图5.将玻璃管整体浸入较热的水中，重新达到平衡.试论证水银柱的位置是否变化？如何变化？

解析：此题同样要构建一物理过程来求解.假设水银柱不动，两部分气体分别做等容过程变化，求出两部分气体压强差的变化，从而判定水银柱的运动情况.

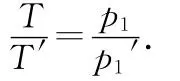
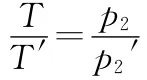
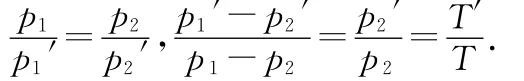
例4.有一水池的实际深度为h，垂直于水面往下看，水池底的视深为多少？已知水的折射率为n.

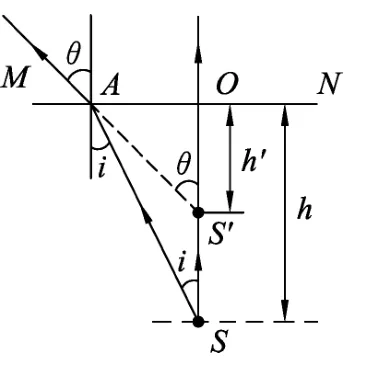
图6

解析：此题需要构建光路折射过程求解.如图6，在水池底构建一点光源S，在由点光源S发出的光线中选取一条垂直水面MN的光线，由水面O点垂直射出，因观察者在S正上方，故另一条光线与SO成极小角度射向水面点A，由A点射到空气中.因入射角i极小，故折射角θ也极小，进入人眼的两条折射光线的反向延长线交于点S′，该点即为我们看到水池底点光源S的像，像点S′到水面的距离h′即为视深.由图6知

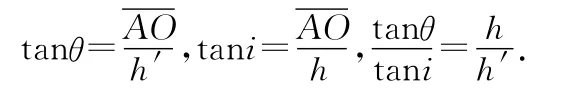
由于θ、i均极小，tanθ≈sinθ，tani≈sini，

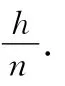
以上的例题可见，熟练掌握好物理基础知识以及知识间的相互联系，对于貌似已知条件不足的问题，能顺利地通过构建物理模型（或者物理过程）来求解.