麦克斯韦方程组及其边值关系独立性的讨论＊

张子珍 林 海 杨成全

（山西大同大学物理与电子科学学院，山西 大同 037009）

电磁场的普遍规律总结为麦克斯韦方程组.在两种介质的分界面上，表征电磁场的麦克斯韦方程组被相应的边值关系所取代.麦克斯韦方程组微分形式的4个式子是不独立的.在时谐电磁波传播时，边值关系的4个式子也不完全独立，而大部分教材只给出了不独立的结果，［1－4］没有加以证明.近年来，也有许多关于麦克斯韦方程组以及边值关系方面的论文，多数是讨论电磁场在分界面上发生突变的原因，对麦克斯韦方程组以及边值关系独立性分析的较少.［5－7］2005年，山东农业大学李慧娟教授对法向边值关系的不独立性作了证明.［8］2010年，华中师范大学物理学院汪德新教授在大学物理的文章［9］提供了一种边值关系不独立性的证明.李慧娟教授提出▽＝▽t＋▽n，在计算散度时，▽t＋▽n还可以理解，但计算旋度时，▽t，▽n分别代表什么？有些困惑.汪德新教授将麦克斯韦方程组的微分形式在分界面的长方体各表面上作了面积分.本文拟从平面波出发对两种绝缘介质的分界面上边值关系不独立性加以证明.

1 介质中麦克斯韦方程组的不独立性

介质中的麦克斯韦方程组为

2 时谐电磁波传播时麦克斯韦方程组的不独立性

在很多实际情况下，电磁波的激发源往往以大致确定的频率做正弦振荡，因而辐射出来电磁波也以相同的频率做正弦振荡.这种以一定频率做正弦振荡的波就是时谐电磁波.其电磁场对时间的依赖关系是E（x，t）＝E（x）e－iωt，B（x，t）＝B（x）e－iωt，即使不是单色波，也可以用傅里叶级数分解为不同频率的正弦波的叠加.线性均匀介质有D＝εE，B＝μH.麦克斯韦方程组变为

很显然，该方程组是不独立的，从（5）、（7）式可导出第（6）、（8）式.

3 边值关系的独立性分析

当电磁波在两种不同介质的分界面上传播时，麦克斯韦方程组被相应的边值关系所取代，两介质分界面上的边值关系如下

时谐电磁波传播时，边值关系的4个式子也是不独立的.下面从平面波出发对两种绝缘介质分界面上边值关系的不独立性加以证明.

在两种绝缘介质的分界面上边值关系为

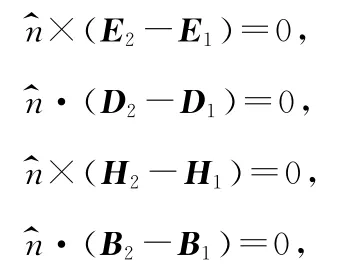
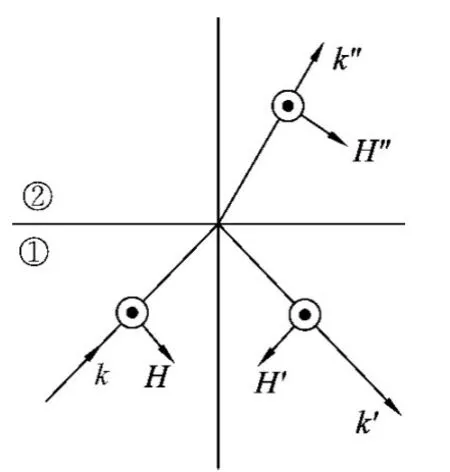
图1

第1种介质和第2种介质中传播的都 是 平 面 波，即E（r，t）＝E0ei（k·r－ωt），H（r，t）＝H0ei（k·r－ωt），分两种情况来考虑.

3.1 E⊥入射面

两边用单位法矢量点乘，得

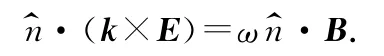
将此式运用在分界面附近的第1种介质与第2种介质中，并相减，得

E平行于界面，故得

即B2n－B1n＝0成立时，E2t－E1t＝0成立.也就是·（B2－B1）＝0成立时，×（E2－E1）＝0成立.

在图1中，D2n＝0，D1n＝0.

3.2 E∥入射面

如图2，可得

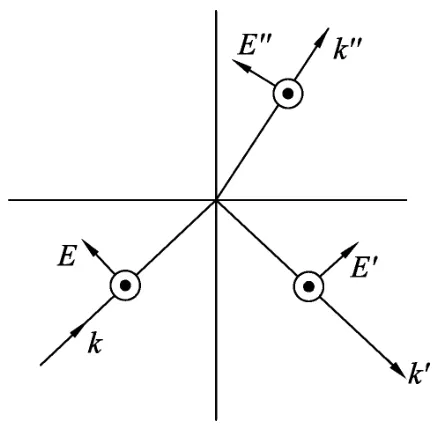
图2

将此式用到分界面处的两种介质中，并相减得

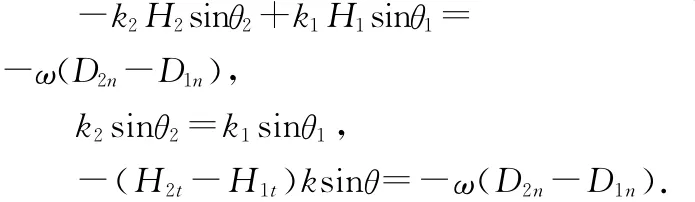
即D2n－D1n＝0成立时，H2t－H1t＝0成立.

也就是说·（D2－D1）＝0成立时×（H2－H1）＝0成立.

在图2中，B2n＝0，B1n＝0.

4 结束语

麦克斯韦方程组的微分形式是不独立的.边值关系也不完全独立.在时谐电磁波传播时，边值关系的4个式子只有两个是独立的，一般来说只考虑两个切向分量即可.

1 郭硕鸿.电动力学［M］.北京：高等教育出版社，2008.06.

2 杨世平，张波，李敬林等.电动力学［M］.北京：科学出版社，2010.02.

3 梁绍荣，王雪君.电动力学［M］.北京：北京师范大学出版社，1986.10.

4 蔡圣善，朱耘，徐建军.电动力学［M］.北京：高等教育出版社，1984.04.

5 江孟蜀.电磁场边值关系的物理起源探讨［J］.重庆工商大学学报，2005，22（1）：20－21.

6 黄凤.电磁场边值关系的讨论［J］.安庆师范学院学报，2012，18（2）：126－128.

7 夏从新，危书义.电磁场切向边值关系的讨论［J］.大学物理，2010，29（1）：21－22.

8 李慧娟.麦克斯韦方程和法向边界条件的非独立性［J］.山东农业大学学报，2005，36（2）：455－457.

9 汪德新.理想导体与均匀绝缘介质界面上边值关系独立性的讨论［J］.大学物理，2010，29（1）：34－35.