关于“时间和空间的相对性”的几个问答

谢礼平

（南京东山外国语学校，江苏 南京 211103）

在高中物理教科书选修3-4狭义相对论内容中，“时间和空间的相对性”是个重、难点，“长度的相对性”的理解是建立在对“同时的相对性”正确理解基础上的，“时间间隔的相对性”也是如此.从逻辑上讲，既然由“同时的相对性”引出了“长度的相对性”和“时间间隔的相对性”，那么，从这条线来叙述时间和空间的相对性就显得很自然，但教科书并不是严密、细致地按照这个思路描述.特别是“长度的相对性”这一内容，对高中生的理解来说有很高的跨度.其他关于狭义相对论的文献，大都单纯利用洛伦兹变换进行数学推导，这种陈述方式固然有其数学上的严密性，但缺乏对物理概念和规律的有效理解，学生难以理解其中的物理意义.这些给一部分学生的学习带来了困难，引起了许多“为什么？”，其中的一些问题，在教师中也易引起争论.本文意图由“同时的相对性”出发，循着狭义相对论的逻辑关系，以师生问答的形式来说明“时间和空间的相对性”.错误或不当之处，敬请指正.

生甲：老师，您在“同时的相对性”中有这样的描述：如图1所示，地面上的人同时看到A、B两处发出的闪光，他会断定：这样的情况下，车厢里面的人是先看到B′端发出的闪光，后看到A′端发出的闪光.我想问一下，这两个闪光到达车厢处人的时间差可以知道是多少吗？

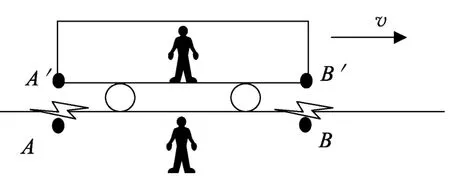
图1

师：这个问题提的很好，问到要害了，先不忙回答你的这个问题，可能其他同学还有相近的问题.

生乙：老师，您说的教科书第100页的图15.2-3所示的例子（参考图2所示），地面上的人在同时测量杆M、N两端，根据前面所讲的同时的相对性，车厢里的人认为，地面上的人是先测量了N端，后测量了M端，设其间隔为Δt，这期间杆已经相对地面向前运动了一段.所以，车厢里的人一定会认为地面测量杆的长度比自己的短，那么，短多少呢？我是这样理解：如果知道了车厢人认为Δt，杆相对地面向前运动的速度为v，那么，地面测量杆长的数值减小量Δl这样表示：Δl＝vΔt，如果车厢里的人测量的杆长为l0，那么，地面人测得的杆长为l，则l＝l0－Δl，您看可以吗？

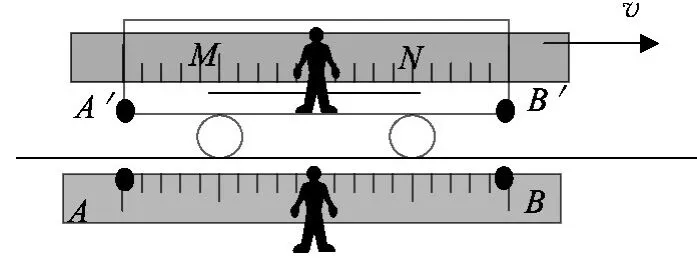
图2

师：请注意，这个长度l是车厢人认为地面人应该测得的杆的部分，这个问题我们稍后说明，除此之外，你是不是想问：怎么才能知道这个时间间隔Δt？

生乙：是的.

师：这就是和甲同学相似的问题了，别的同学还有问题吗？

生丙：老师，关于时间间隔的相对性问题，我看了些参考书，有这么个例子：如图3（a）所示，列车以速度v相对地面匀速行驶，车厢底面装有一光源O，紧靠它有一标准钟，该底面的正对面的车厢顶部装一平面镜M，可使向上发出的光脉冲原路返回，光速为c且不变，设车厢的高度为b，光脉冲在车厢往返过程中，车上的钟走过的时间为Δt′，但是地面的人观看，由于列车在前进，光线走的是锯齿形路径，如图3（b）所示，光线来回一次的时间为Δt，这是地面钟的时间间隔.

图3

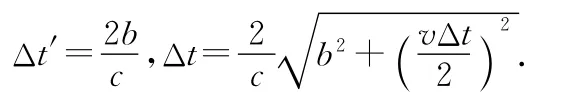
由此可得两个参考系时间间隔的关系为

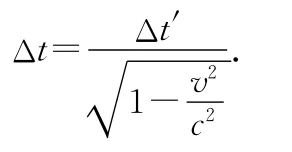
我的问题是：这个过程我看得懂，但我感觉莫名其妙，这个例子有一般性吗？为什么可以这样说明？您能帮我从另外一个途径说明时间间隔的相对性吗？

师：好的，很高兴你对相对论有这样浓厚的兴趣.从上面的几个问题可以看出，同学们在理解了同时的相对性之后，开始关心它们之间的定量关系了.这些问题实际上也就是寻找在两个参考系中时间的转换关系，有难度.我们先根据同时的相对性来说明某一事件的“时刻”和“位置”在两个参考系中的是如何转换的.下面借助于一个我们熟悉的物理情景来进行.如图4（a）所示，火车以速度v向右高速运动，当位于车厢中部的人与地面人位于同一水平位置时，分别以两人位置为原点建立一维空间坐标，并设此时为0时刻，此时在车厢的中部发出一个闪光，这个闪光会到达车厢右端B′处.对这个事件，根据我们在同时的相对性中形成的认识，车厢人和地面人会有不同的描述.设地面人认为这个事件为（x，t），而车厢人认为这个事件为（x′，t′），下面讨论它们间的关系.期望得到两个参考系时刻与位置转换关系式，你们看应该怎么开始？

图4

生甲：我感觉一头雾水，不过，我猜测，得先考虑两个参考系中各物理量的关系吧？

师：对，你的猜测非常好.那么它们到底哪些物理量有关系呢？又有什么关系？

生甲：如您在上节课所说，根据相对性原理和光速不变原理，在各自参考系中，物理规律不变，光速不变.至于别的，就得分析了.

师：很好，对于其他物理量如位置、时刻，我们就不能认为它们是相同的，得想办法找到它们间的关系.

生：……

师：情况也不是一筹莫展，如图4（b）所示，对地面人来说，B′距离他为ct，对于车厢人来说，地面人向左运动了vt′，车厢右端距离他为ct′，如甲同学刚才所说，它们间的关系不能理解成ct＝vt′＋ct′，但可以假设它们间有正比例关系，表示为ct＝k（vt′＋ct′）.

生甲：老师，要这么说的话，你在相对论两个假设的基础上，又添了一个假设哦.

师：是的，以后你会知道，这叫“时间、空间的均匀性以及空间的各向同性”假设；你很严谨，学习相对论需要这样的严谨.

师：同理，我们还可以得出，ct′＝k（ct－vt）.与上式相比较，其比例系数认为相等，理由是在各自的参考系中观察，它们是等价的.如此，就可以推导两参考系时刻t和t′、位置x和x′之间的关系了.

生乙：我整理一下，

师：可以看出，要定量确定两参考系事件发生的位置x、x′和时刻t、t′之间的关系，关键是要确定常数k.

生乙：哦，是的，由（1）、（2）、（3）式可得

由（1）、（2）、（4）式可得

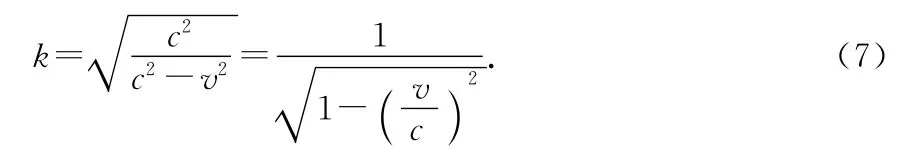
为了得到时刻和位置的关系，将（7）式代入（3）、（4）式，求解x、x′、t和t′，可得

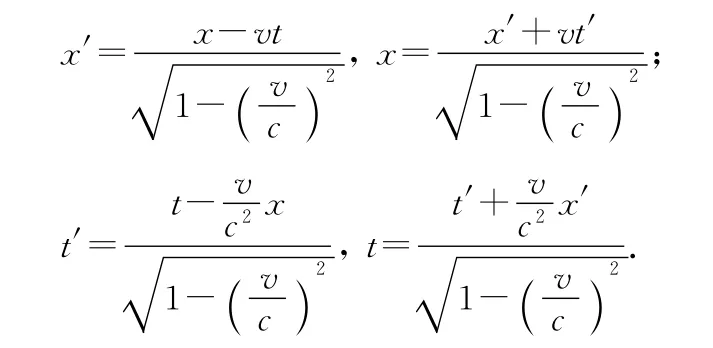
生丙：老师，这样的推导过程，我觉得比较自然了，但这几个公式的物理意义是什么？它们能解决刚才我提出的问题吗？

师：首先，它们可帮助我们确定在车厢中发生的一个事件，车厢人与地面人对此不同描述以及它们间的关系.由此就可确定两个事件的长度（位置间隔）在不同参考系之间的变换关系，也就是Δx′与Δx之间的关系.同理，还可确定两个事件发生的时间间隔在不同参考系之间的变换关系.其次，时间和空间不再各自独立地存在，两者由于惯性参考系的相对运动而有机地结合在一起，时间、空间和物质运动之间的有密切的关系，这就是狭义相对论时空观.最后，值得一提的是，时间和空间的相对性只发生在运动方向上.在同时的相对性中已经说过，在垂直运动方向上，同时是一致的，因而在这些方向上，时间是同步的，长度也是一样的.

师：至于你提出的第二个问题，你可以引用上面的变换式

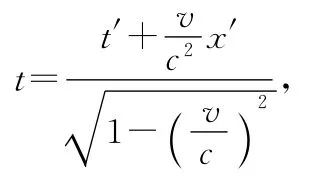
推导一下Δt和Δt′的关系.提示：在车厢参考系中，发出光脉冲和接受光脉冲是在同一个位置，即Δx′＝0，这也是选用这个变换式进行计算的原因.甲同学第一个提出的问题，实际是求Δt′.你知道吗？

生甲：嗯，问题条件是Δt＝0，Δx′为车厢自身长度，那么选择公式

就可解决它.公式

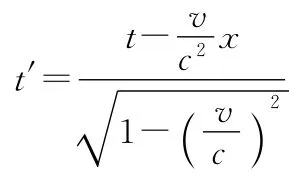
有点麻烦，因为需要确定Δx，应该比车厢本身长度短点.

生乙：老师，我前面问到的长度的收缩，根据这些变换式，能得到吗？

师：对照图2所示的例子，车厢人测量车厢内杆的长度为l0，地面人的测量必须要同时对准杆的两端才行（车厢人测量杆长是不需要同时的，只要与尺子两端对齐，读出两个位置的刻度值即可），即tN＝tM，车厢人是怎么看待地面人的测量的呢？根据同时的相对性，车厢人认为地面人先对准了N点，后对准了M点，也就是说车厢人认为地面人对准M点的时刻后发生，即tM′＞tN′，在这个时间差Δt′内，杆向前移动了一段距离，数学表述是

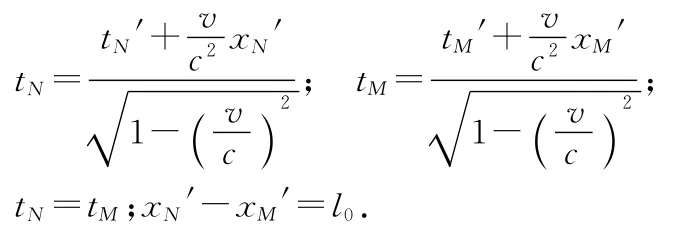
可得

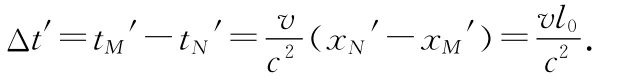
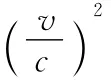
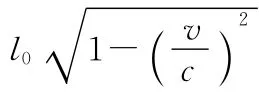
师：L是指车厢人认为地面人所测得的杆的部分，车厢人可不认为地面人的测量数据仅仅是少了一部分杆长，地面上的任何相对于火车运动方向上的尺寸全都收缩了，也即，车厢人还看到地面人所用的尺子也收缩了，对此，车厢人是这么看的：地面的尺子高速向左运动，两端为A和B，车厢尺子两端A′和B′同时与其对齐，即必须有tA′＝tB′，故我们用代换

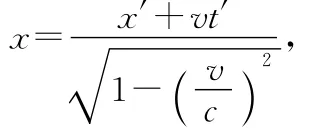
可以得到

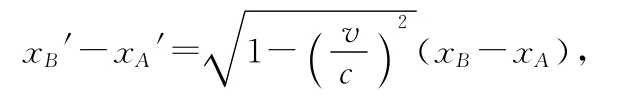
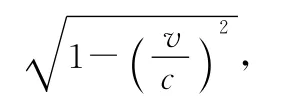
地面测量值就应该是

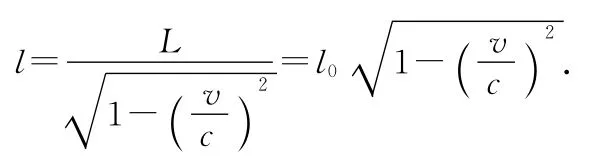
生甲：要这么费劲啊，地面人直接到车厢上来测量不就行了吗？

师：这样的话，他测量到的就是原车厢人测量杆的长度，但我们的目标是测量一个相对于测量者运动杆的长度，所以就比较“费劲”.另外，地面人测量值你也可用公式

得到，此处有Δt＝0，Δx′＝l0.

生甲：车厢人认为的地面人的测量结果，还是相对论理论上的结论，这需要实验的验证，是吧？

师：很好，是的.

1 赵凯华，罗蔚茵.新概念物理教程，力学（第2版）［M］.北京：高等教育出版社，2012.

2 张之翔.对长度收缩的另一种看法［J］.大学物理，2005（10）：13－14.

3 邱会明.洛伦兹变换的推导及对其悖论的解释［J］.中学教学参考，2012（2）：62.

4 谢礼平.关于“同时的相对性”的几个问答［J］.物理教师，2014（5）：18.