应用基于核序列的区间灰数模型预测地下水位动态
陈 勤
(三峡大学科技学院,湖北 宜昌 443002)
地下水位动态是地下水动态最主要的指标,对地下水动态进行预测是正确认识地下水资源形成及其性质最有效的方法之一[1]。有许多学者对地下水位动态进行了预测,常见的预测方法包括回归分析、时间序列分析、有限差分法。文献[2-3]应用灰色GM(1,1)模型对地下水位动态进行了模拟和预测,结果令人满意。但目前的研究成果大部分以“实数”为灰色建模前提,而以“灰数”为建模对象预测地下水位动态的文献尚少。本文探讨采用区间灰数Verhulst模型对地下水位动态进行预测,证明该模型的可行性和实用性。
1 灰色Verhulst模型
设原始非负序列 X(0)={x(0)(1),x(0)(2),…x(0)(n)}的一阶累加生成序列:

Z(1)为 X(1)的紧邻均值生成序列:
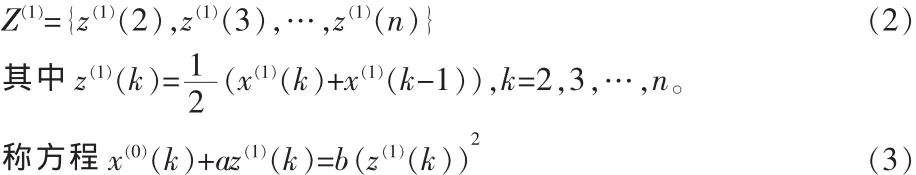
为灰色Verhulst模型。
根据式(1)利用最小二乘法,估计出参数a、b的值,得:
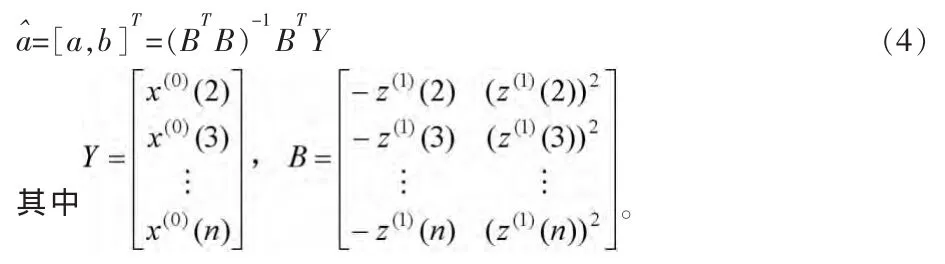
为灰色Verhulst模型的白化方程,也称影子方程。
设B,Y,a^如上所述,则灰色Verhulst模型的白化方程式(5)的解为:

灰色Verhulst模型的时间响应式为:

2 区间灰数Verhulst模型
定义1 既有下界ak,又有上界bk的灰数称为区间灰数,记作⊗k∈,其中 ak<bk。
定义2 在区间灰数⊗k缺乏取值分布信息的情况下,若⊗k为连续灰数,则称为区间灰数⊗k的核。
定义 3 由区间灰数⊗k∈[ak,bk](k=1,2,…,n)构成的序列称为区间灰数序列,记作 X(⊗)={⊗1,⊗2,…,⊗n};在区间灰数序列 X(⊗)中,根据定义 1,由每个区间灰数⊗k的核⊗~k所构成的序列称为 X(⊗)的核序列 X(⊗~),记作。
定义4[4]区间灰数⊗k的上界bk与下界ak的差值称为区间灰数⊗k的信息域或区间域,记为dk=bk-ak。区间灰数序列X(⊗)中所有灰元的信息域dk所构成的序列称作X(⊗)的信息域序列,记作Xd=
。 区间灰数⊗^ (tk+1)预测值的信息域
定理 1 设⊗k为连续灰数,且,又为灰数的核,为灰数的信息域,则有:

区间灰数序列的Verhulst模型建立如下:

其中,Z(1)为的紧邻均值生成序列。
利用最小二乘法,估计出参数a,b的值,得:
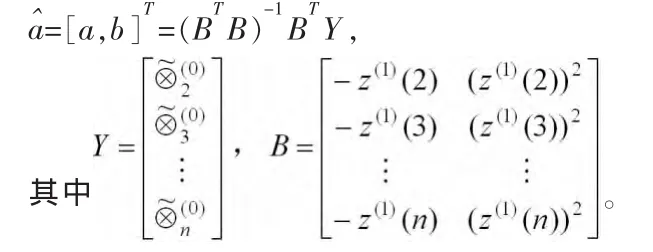
区间灰数的Verhulst模型为:
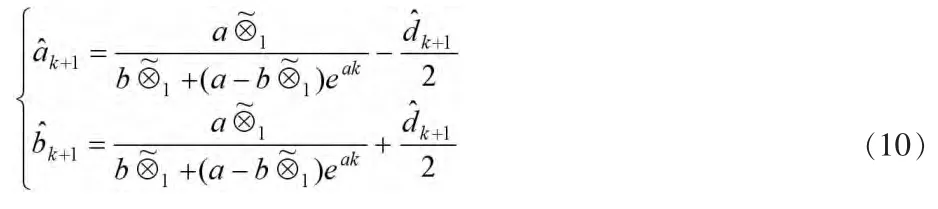
3 应用分析
下面通过对某盆地下游湖区站点地下水位埋深建立区间灰数Verhulst模型,验证该模型在解决实际问题时的可行性和实用性。

表1 某盆地下游湖区站点地下水位观测结果的区间灰数值
由表 1,可得区间灰数序列 X(⊗)={[18.06,18.40],[18.43,18.75],… [29.01,29.25]}, 根据定义 2 和定义 3,X (⊗) 的核序列{18.23,18.59,19.24,19.91,22.48,27.45,28.59,28.72,29.13}。
图1表明核序列表现出近S形特征,符合Verhulst模型的建模条件,可以对其建立Verhulst模型。计算模型参数,得a=-0.1406,b=-0.0034,由式(9)可得核序列的灰色Verhulst模型为:

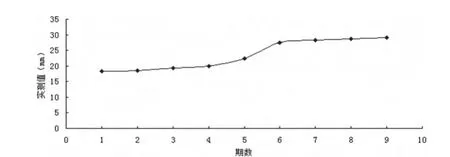
图1 核序列的近似S形特征

表2 某盆地下游湖区站点地下水位预测值
信息域由定义 4确定,d^k+1=d1∨d2∨…d9=0.82,由式(10)得:

经计算,核序列Verhulst模型的平均相对误差接近二级,可用于预测,见表2。
4 结论
基于核序列的区间灰数Verhulst模型应用于地下水位动态的预测,具有运算方便、易于检验等优点,验证了该模型的有效性和实用性,满足了灰色系统理论中越来越常见的区间灰数序列预测的需要。
[1]陈葆仁,洪再吉.地下水动态及其预测[M].北京:科学出版社,1988.
[2]富飞.灰色GM(1,1)模型在地下水位动态预测中的应用[J].地下水,2014(1).
[3]杨建飞,刘俊民,陈琳.基于灰色残差模型的灌区地下水最小埋深预测[J].人民黄河,2011(7).
[4]杨德岭,刘思峰,曾波.基于核和信息域的区间灰数Verhulst模型[J].控制与决策,2013(2).

