应力释放技术识别在役钢筋混凝土构件内力(I)——方法研究

鲁 亮 李 鸿 刘纪军

(1.同济大学结构工程与防灾研究所，上海200092;2.上海市机电设计研究院有限公司，上海200040)

1 引 言

我国城镇现有存量建筑总面积超过200亿平方米，由于设计、施工、寿命期等各种原因，有15%以上的建筑需要检测、鉴定与加固。在西方发达国家，建筑维修和加固费用约占其土建总投资的50%。既有建筑、桥梁等混凝土结构的安全性评估中，混凝土结构的受力状态是一个十分重要的评估内容。目前钢筋混凝土结构的安全性评估主要以分析计算为主［1］，辅以静载试验和材料强度检测结果，所建立的数值分析模型是处于理想状态的，没有充分考虑影响构件内力状态的不利因素，比如施工带来的尺寸偏差、外加荷载分布的不均匀性、材料特性在整个结构内分布的均匀性、结构的变形状态等。用处于理想状态的分析模型计算得到的构件内力比实际内力偏大或偏小，依据计算结果进行结构加固不能保证结构的抗震承载力安全，所以需要寻找一种现场实测构件内力的方法。构件表面应力释放法是一种值得探讨的现场实测方法，采用应力释放法测试混凝土表面工作应力，抽样测试结果可以与计算结果进行比较，并可以用来对整个结构的内力计算结果进行修正，最终得到符合实际的构件内力分布［2］。

表面应力释放法广泛应用于钢构件表面残余应力的测试，已有相关测试规范和标准，是一种比较成熟的测试技术。表面应力释放法用于测试混凝土表面工作应力尚有技术和理论上障碍，已有学者进行了相关研究［3］，但是研究成果离工程应用尚有一定距离。本文就应力释放技术用于测试混凝土构件内力的基本原理做理论阐述。

2 应力释放法测试在役构件表面应力

应力释放法是在构件表面钻一个小孔或开一根槽，使得孔边或槽边应力得以释放，通过应变电测的方法得到释放应变后反推测点表面原有应力的方法。应力释放的方法有很多种，常用的有钻孔法、盲孔法、环孔法、开槽法等。钻孔法和盲孔法是两种常用的应力释放方法，该方法最早是由德国学者Mathar于1934年提出［4］，后经Soete［5］等学者发展完善而形成系统理论。1981年美国材料与试验协会将盲孔法纳入ASTM标准E837-81［6］，1992年中国船舶工业总公司也将其制定为残余应力测试的中国船舶行业标准CB 3395-92［7］。此两种方法主要用于金属材料表面应力的测试。由于混凝土材料是非匀质材料，研究表明用钻孔法或盲孔法得到的测试结果离散性很大，所以研究人员尝试采用环孔法和开槽法测试混凝土表面应力。

2.1 环孔法

环孔法是由Milbred于1951年提出来的，其基本原理是对有初始约束应力的测试构件，采用机械切割的方法在测点的周围切割一圈，解除测点周围的应力约束，圈内的应力逐步被释放。在圈内贴上应变计，测得释放的应变，即可算出表面的应力大小。该种方法原理比较简单，国内有学者采用此方法在混凝土构件应力测试方面做了相关研究。翁冠群［8］利用MSC/NASTRAN有限元软件得出应力释放至零点的环孔深度与环孔直径的数值关系，指出100 mm外径的环形钻孔其深度在30～35 mm之间时应力逐渐释放至零，并将环孔法用于桥梁预应力损失的检测中，同时指出33 mm可以作为合适的开孔深度。刘永淼［9］采用混凝土取芯机开环孔实现应力解除，在试验室完成了既有混凝土构件正应力测量试验。

环孔法操作简单、易行，缺点在浇筑构件时需预埋导线，否则采集释放数据时在布线方面存在困难，故此方法可用于试验室科学研究，不易在实际工程中推广使用。

2.2 开槽法

开槽法是由环孔法发展而来。该方法用四条长槽解除测点约束，该处的应力即被释放，原应力场失去平衡，这时测点周围将产生一定量的释放应变(其大小与释放应力是相对的)，并使原应力场达到新的平衡，形成新的应力场和应变场。测出释放应变Δε，即可利用相应公式计算出初始测试点的应力。对于图1所示应变计测得的释放应变，其应变计算公式为［10］

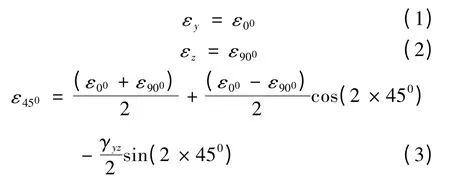
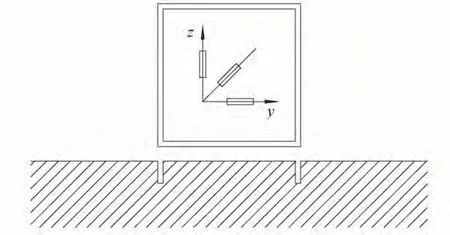
图1 开槽法的应变计粘贴方式Fig.1 Strain gauges paste way of grooving method

由于测量γyz比较困难，通常的做法是测定三个方向的线应变，由这三个方向的线应变，反解出γyz:

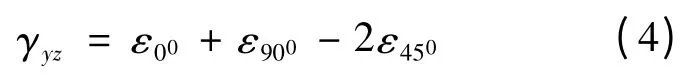
在求得测点的应变后，利用平面应力状态时的胡克定律，求得测点的应力:

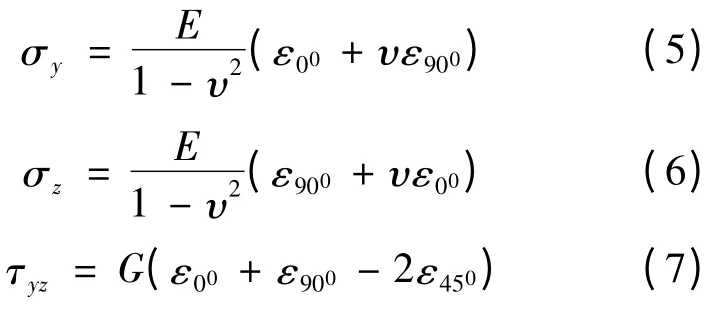
式中，E，ν，G分别为被测材料的弹性模量、泊松比和剪切模量。

从上面推导可知，工作应力测试的结果主要与两个因素有关，第一个因素是材料属性，第二个因素是电阻应变片的测量值。

应用应变电测法可以测出以上释放应变值，此值是否是构件表面原有应变释放至零的应变值，有待进一步试验或数值分析研究。此释放应变值与槽距、槽宽、槽深等因素有关，同时在应变测试过程中会受到振动扰动、温度变化、混凝土浸水等的影响，也有待进一步探讨。

国内有学者采用此种方法在混凝土构件正应力测试方面做了相关研究工作。沈旭凯［11］通过对5根混凝土柱进行开槽法应力释放研究，指出采用开槽法进行应力释放可以得到与环孔法一样的效果;王柏生等［12］采用切割两条长槽的方式释放混凝土构件的正应力，通过有限元软件分析了工作应力随开槽深度的变化规律，与环孔法进行了比较，得到了正应力完全释放的开槽深度;并且在分析了各种影响因素后，就开槽引起的扰动应变展开试验研究，据此估计检测时的扰动应变，并进行了验证性试验，消除了检测结果中的扰动应变，取得了满意的结果。

3 既有钢筋混凝土构件内力识别基本理论

建筑结构混凝土构件的基本形式有梁、柱、板、墙四种，四种构件形式截面内力分量的数量不同，墙主要有面内剪力和弯矩，板主要有面内轴力和面外弯矩，而梁、柱最多有轴力、双横向剪力、双横向弯矩和扭矩六个内力分量，下面以一个含钢筋截面的混凝土柱为例，见图2，推导在内力作用下产生于构件表面中点处的正应变和剪应变公式，再由测试得到的释放应变值反推构件截面内力值，以证明表面应力释放技术的可行性。

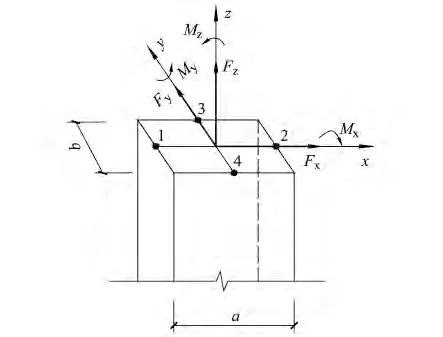
图2 矩形截面构件受力简图Fig.2 Force diagram of rectangular section member

3.1 钢筋混凝土矩形截面构件在轴力、弯矩作用下的应力表达式

在图2所示轴力Fz、作用下，截面四边中点1、2、3、4处仅产生正应力，如下:

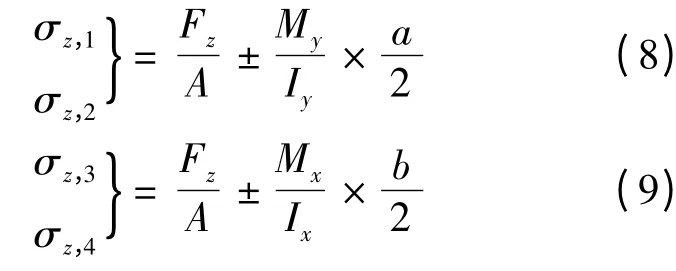
式中 a、b——截面边长;

3.2 均质材料矩形截面构件在扭矩作用下的剪应力表达式

扭矩作用下含钢筋截面的剪应力公式推导相对复杂，先从匀质材料开始，最后考虑用修正的方法得到含钢筋截面的剪应力表达式。由于非圆截面构件扭转时截面将发生翘曲，作为材料力学一维简化理论之基础的平截面假定不再适用，所以非圆截面构件的扭转问题要用二维弹性力学方法来推导。

矩形截面构件受扭矩Mz作用，如图3所示，其剪应力表达式为［13］

式中，G为材料的剪切模量，

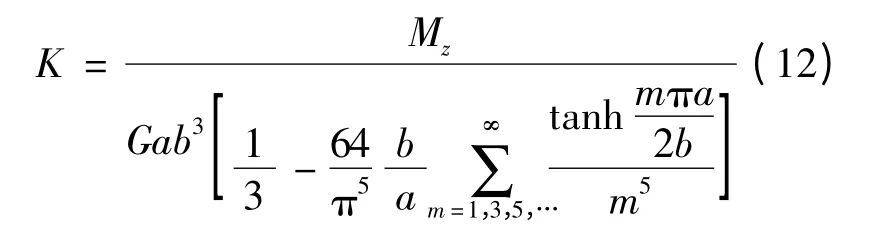
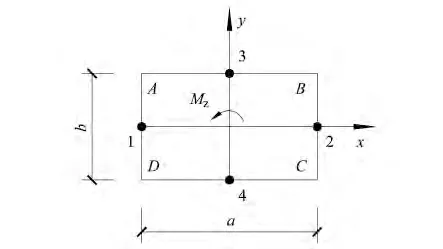
图3 矩形截面构件受扭Fig.3 Rectangular section member subjected to torsion

令式(10)中y=±b/2，得到AB、CD边的剪应力表达式:

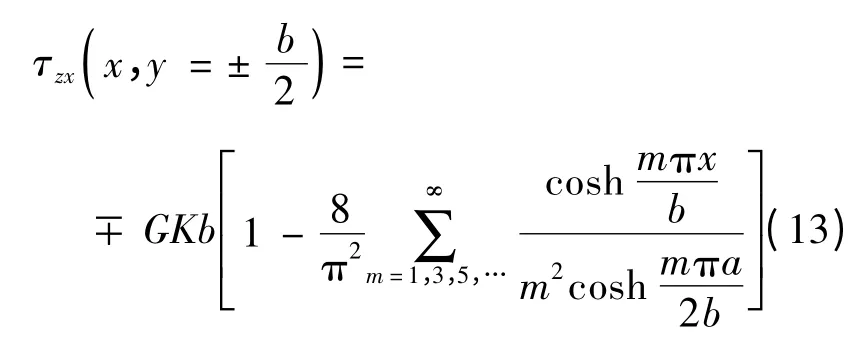
令式(11)中x=±a/2，得到BC、AD边的剪应力表达式:

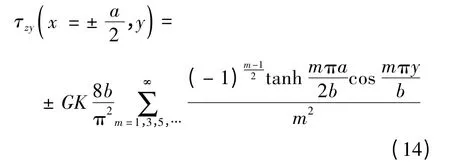
最大应力发生在长边中点处，令式(10)中x=0，y=±b/2，得到点3处和点4处的应力值，也即最大应力值:

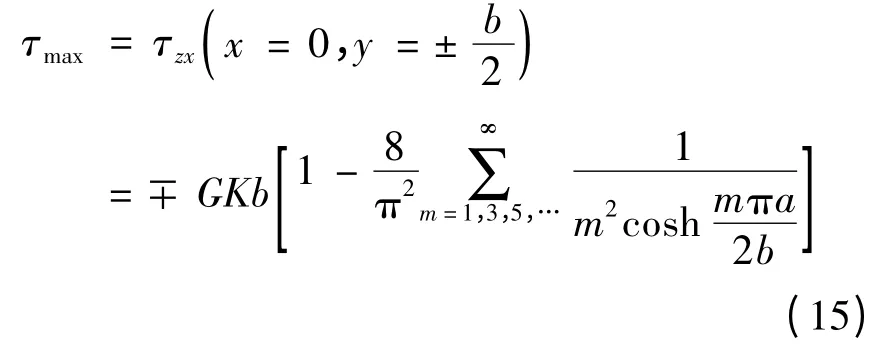
短边的最大剪应力发生在短边中点处，令式(11)中x=±a/2，y=0，得到点1处和点2处的剪应力值:

实际应用中，记

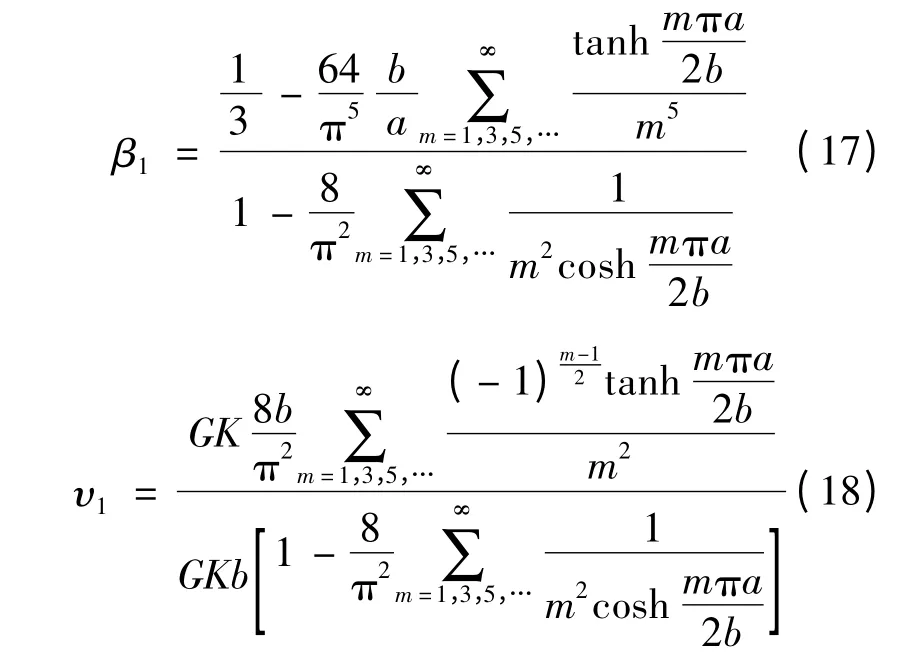
则式(15)、式(16)简化为

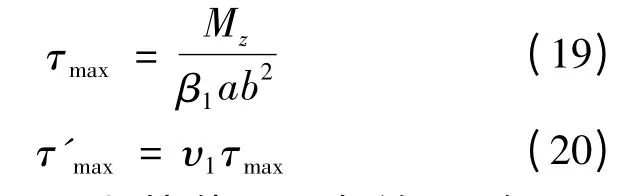
则因子β1，υ1只与比值a/b有关，两个因子的计算示例如表1所示。

表1 矩形截面构件受纯扭时的系数β1和υ1Table 1 Factorβ1 andυ1 of rectangular section members under the action of pure torsion

弹性力学的分析结果表明，矩形截面构件在扭转时，其横截面上的剪应力分布具有以下特点:

(1)截面周边各点处的剪应力方向与周边相切，且截面顶点处的剪应力为0;

(2)最大剪应力发生在长边中点处，而短边中点处的剪应力则为该边上剪应力的最大值;

(3)截面中心与顶点的连线上，剪应力先增大后减小。

剪应力分布如图4所示［14］，最大剪应力τmax和短边中点处剪应力可根据式(19)、式(20)计算得到。

3.3 均质材料矩形截面构件在剪力作用下的剪应力表达式

材料力学中的剪应力公式适用于狭长矩形截面构件，当不满足这一条件时，用于推导剪应力公式的两个假设不再成立(两个假设内容:假设矩形截面上剪应力方向和剪力方向相同;假设截面上剪应力沿厚度是均匀分布的)。弹性力学给出了适用于一般矩形截面构件的剪应力公式，受力如图5的构件截面的弹性力学解为［15］

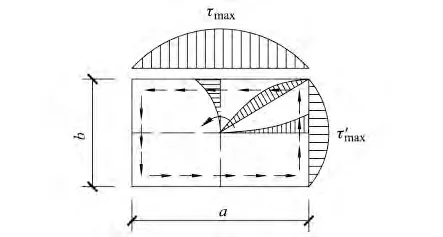
图4 矩形截面构件受扭时剪应力分布Fig.4 Shear stress distribution of rectangular section members subjected to torsion

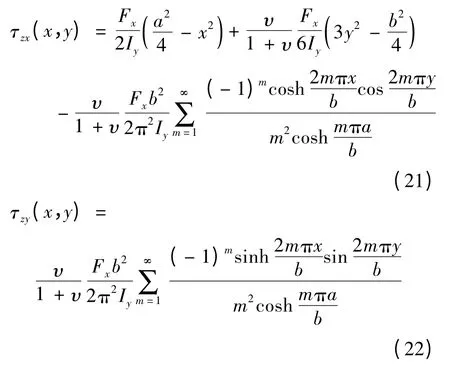
图5 矩形截面构件受剪Fig.5 Rectangular section members subjected to shear

式(21)第一项为基本部分，是狭长矩形截面构件剪应力的解式，经过第二、三两项的修正适用于一般的矩形截面构件。弹性力学计算表明，当a/b≥2时，第二、三两项所占比重很小，取第一项即可满足工程精度的需要，其退化为材料力学矩形截面构件剪应力公式;当不满足a/b≥2时，式(21)中第二、三两项所占比重不能忽略。

令式(21)中x=0，y=±b/2，得到点3处和点4处剪应力值，即最大剪应力值:

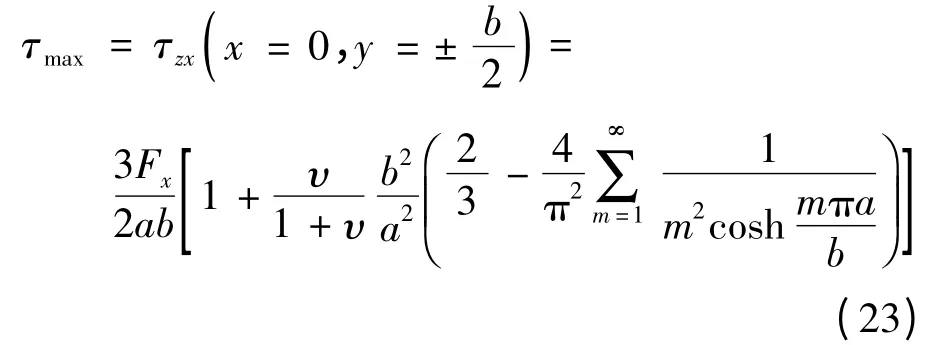
令式(22)中x=±a/2，y=0，得到点1处和点2处剪应力值:

实际运用中，令

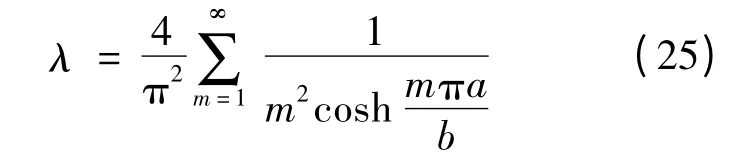
则式(23)可以简化为

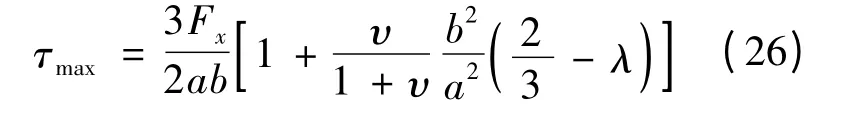
为方便应用，将对应于不同高宽比a/b的λ制成表格，如表2所示。

表2 矩形截面构件剪应力系数λTable 2 Shear stress factorλof rectangular section members

上面讨论的是外力F平行于x轴的情况。当外力F平行于y轴时，可类似地导出截面内应力计算公式;当外力F通过弯曲中心，但不平行于形心轴x或y时，把F沿x轴和y轴分解成Fx和Fy，分别计算两个平面弯曲问题，然后叠加;当外力F不通过弯曲中心时则出现弯扭耦合变形，这时可先把F平移到弯曲中心上，按斜弯曲处理，然后再叠加由F对弯曲中心的力矩所引起的扭转应力。

3.4 钢筋混凝土矩形截面构件在扭矩、剪力作用下的应力表达式

钢筋混凝土矩形截面构件受扭时，在弹性阶段钢筋与混凝土变形协调，整个截面的抗扭分为钢筋抗扭和混凝土抗扭两部分。根据匀质材料矩形截面构件扭矩作用下剪应力公式(19)，扭矩作用下钢筋混凝土矩形截面构件在弹性阶段可如式(29)的方式近似考虑钢筋的抗扭贡献。

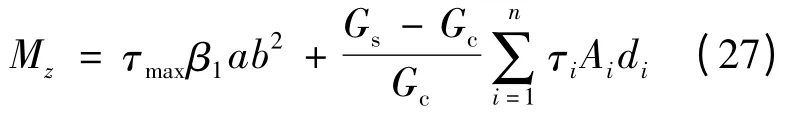
式中，Gs为钢筋剪切模量;Gc为混凝土剪切模量;n为钢筋的根数;τi为扭矩作用于匀质材料矩形截面构件时第i根钢筋形心位置的剪应力(以下称之为钢筋的抗扭名义剪应力);Ai为第i根钢筋的面积;di为第i根钢筋形心到截面形心的距离。

假设第i根钢筋的位置(xi，yi)，此钢筋两个方向的抗扭名义剪应力为τzx(xi，yi)和τzy(xi，yi)，则:

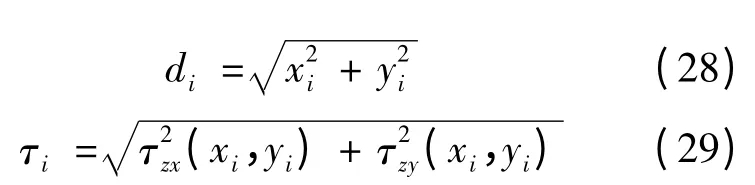
式中，τzx(xi，yi)，τzy(xi，yi)按式(10)、式(11)计算。

定义

在截面长宽比确定的情况下，ηi仅与钢筋所处的位置有关，称之为钢筋的抗扭位置系数，且式(27)简化为

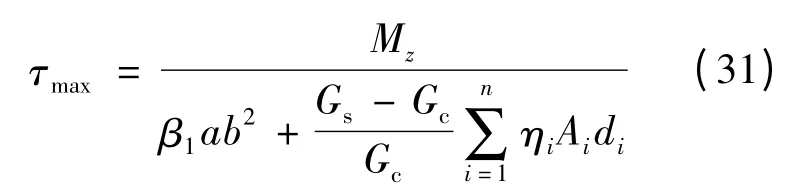
由匀质材料矩形截面构件剪力作用下剪应力公式(26)，采用同样方法考虑剪力作用下钢筋混凝土矩形截面构件钢筋的抗剪贡献，如下式所示:

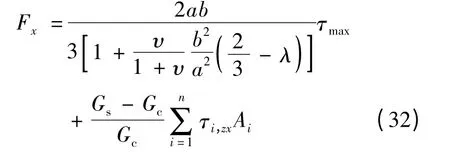
式中，τi，zx为剪力作用于匀质材料构件时第i根钢筋形心位置x方向的剪应力(以下称为钢筋的抗剪名义剪应力)，按式(19)计算。

定义

在截面长宽比确定的情况下，λi仅与钢筋所处位置有关，称为钢筋的抗剪位置系数，且式(32)简化为

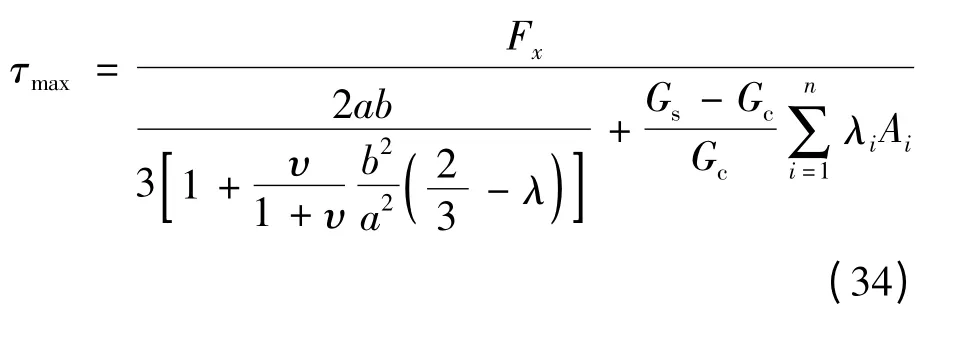
钢筋的抗扭位置系数ηi和抗剪位置系数λi数值根据以上相关公式计算即可。例如，一个长为a=500 mm、宽为b的矩形截面，钢筋位置及编号如图6所示，钢筋直径为20 mm，保护层厚度为30 mm，钢筋的抗扭位置系数和抗剪位置系数计算结果分别见表3、表4。

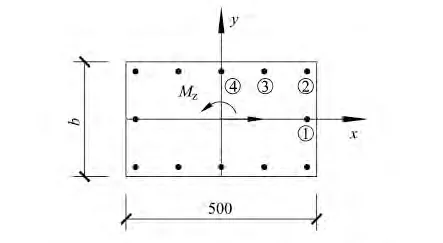
图6 矩形截面钢筋位置Fig.6 Steel bar position of rectangular section members

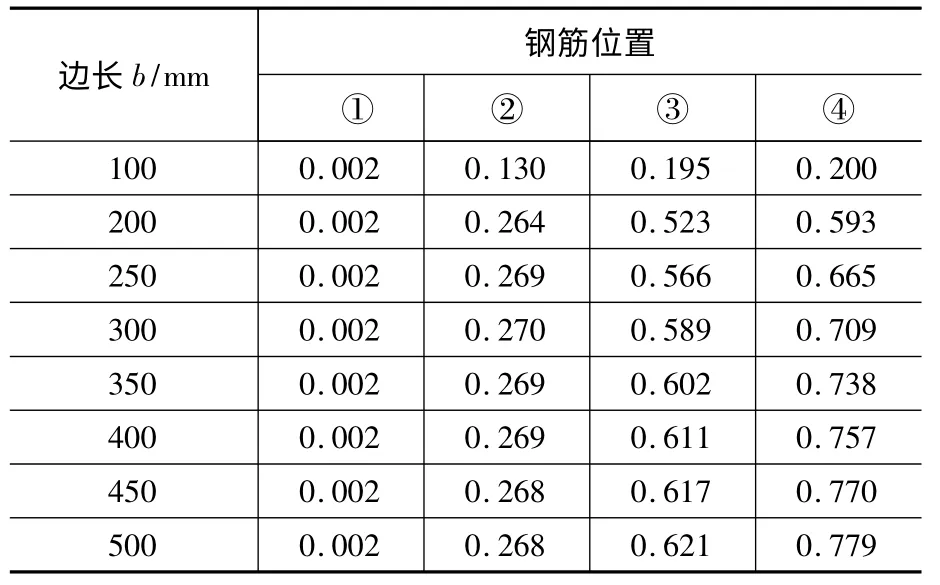
表3 钢筋抗扭位置系数ηiTable 3 Position factorηi of steel bar subjected to torsion

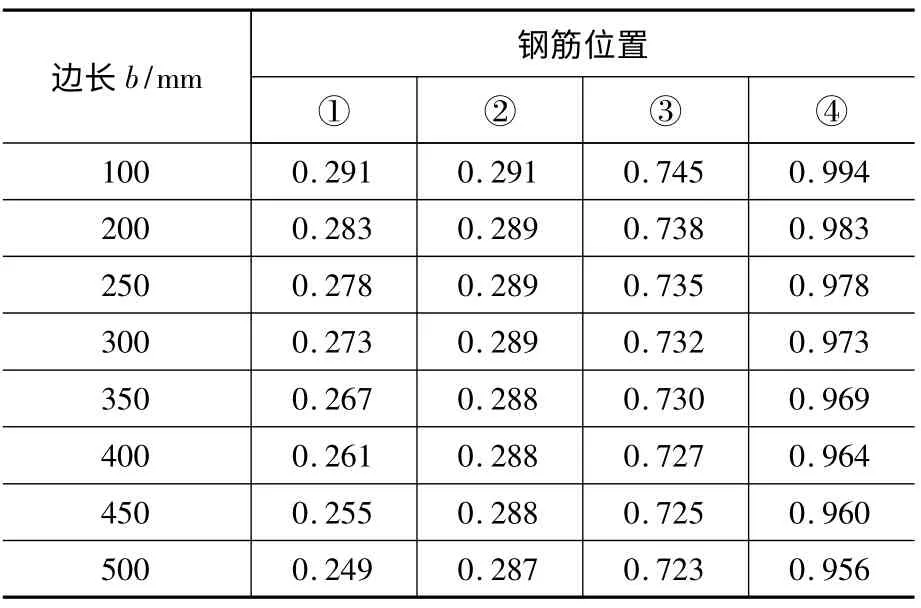
表4 钢筋抗剪位置系数λiTable 4 Position factorλi of steel bar subjected to shear

在小变形条件下，利用叠加原理写出图2截面中点1、2、3、4的剪应力表达式如下:

3.5 钢筋混凝土矩形截面构件内力识别

联立式(8)、式(9)中任意三个即可求得Fz;Mx和My，如联立前三个求得:

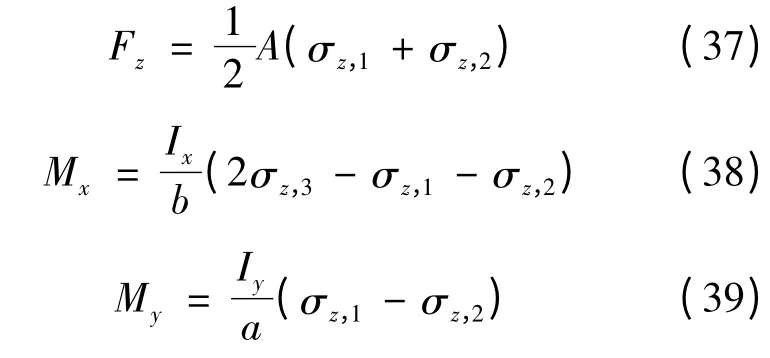
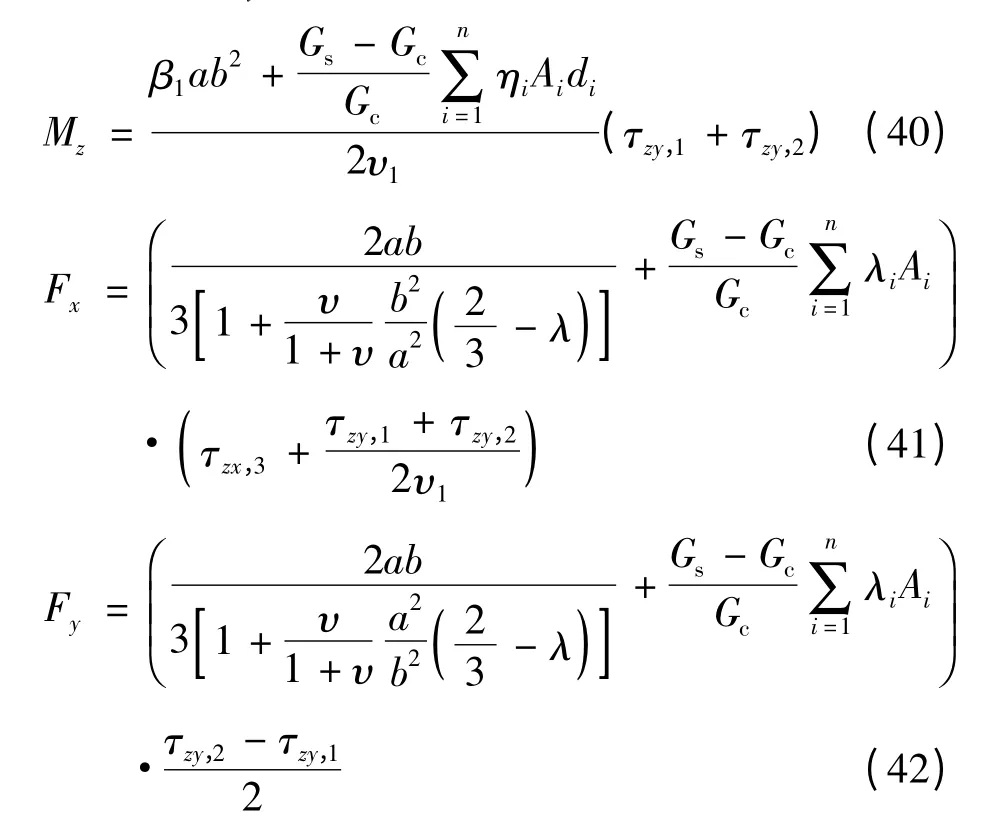
联立式(35)、式(36)中任意三个即可求得Mz、Fx和Fy，如联立前三个求得:

以上公式中的应力由应变花测得的应变通过式(5)—式(7)求得;β1，υ1查表1得到，λ查表2得到，ηi查表3得到，λi查表4得到;a为矩形截面构件的长边，b为矩形截面构件的短边，di，x，di，y分别为第i根钢筋到相应中性轴的距离。

由上面的推导可以看出，只要由应力释放法得到图2截面上1—4点中任意三点的表面应力，即可以计算出该截面的所有内力分量。

4 结 语

介绍采用应力释放技术测试钢筋混凝土构件表面应力的基本方法。理论推导了构件截面各内力分量作用下截面各边中点处的正应力和剪应力，证明了只要测试出一个矩形截面三个边中点处的正应变和剪应变值，就可以识别出截面内力。

［1］ 刘纪军，鲁亮，王辉.应力释放法识别既有钢筋混凝土构件工作应力的有限元分析［C］.第20届全国结构工程学术会议论文集Ⅰ，2011:366-371.Liu Jijun，Lu Liang，Wang Hui.Finite element analysis on the working internal forces in existing RC member by stress-release method［C］.Proceedings of the Twentieth National Conference on Structural EngineeringⅠ，2011:366-371.(in Chinese)

［2］ 刘纪军.应力释放法识别既有钢筋混凝土构件内力试验研究与分析［D］.上海:同济大学，2012.Liu Jijun.Analytical and experimental study on internal forces measurement in existing reinforced concrete members by stress-release method［D］.Shanghai:Tongji University，2012.(in Chinese)

［3］ 时蓓玲，吴锋，孙穆.既有混凝土结构现存应力测试方法研究［J］.水运工程，2011，449(1):131-135.Shi Beiling，Wu Feng，Sun Mu.On the testing method for the existing stress of concrete structures［J］.Port and Waterway Engineering，2011，449(1):131-135.(in Chinese)

［4］ Mathar J.Determination of initial stresses by measuring the deformations around drilled holes［J］.Trans.ASME，1934，4:249-254.

［5］ Soete W，Van Crombrugge R.An industrial method for the determination of residual stresses［J］.Proc.SESA，1950，8(1)，17-26.

［6］ ASTM International E837 Standard test method for determining residual stresses by the hole-drilling strain gage method［S］.West Conshohocken，PA，USA:ASTM，2002.

［7］ 中国船舶工业总公司.CB 3395—92残余应力测试方法钻孔应变释放法［S］.北京:中国标准出版社，1992.China State Shipbuilding Corporation.CB 3395—92 Residual stress determination method hole-drillingstrain-release method［S］.Beijing:Standards Press of China，1992.(in Chinese)

［8］ 翁冠群.桥梁预力损失检测技术及安全评估［C］.2001年全国公路桥梁维修与加固技术研讨会，2001.Weng Guanqun.Prestress-lossing detection technology and security assessments of bridges［C］.The highway bridge repair and strengthen technical seminar，2001.(in Chinese)

［9］ 刘永淼.环孔法测试混凝土工作应力试验研究［D］.杭州:浙江大学，2006.Liu Yongmiao.Experimental research on the working stress measurement of concrete by the ring-hole method［D］.Hangzhou:Zhejiang University，2006.(in Chinese)

［10］ 宋子康，蔡文安.材料力学［M］.上海:同济大学出版社，1998.Song Zikang，Cai Wenan.Mechanic of materials［M］.Shanghai:Tongji University Press，1998.(in Chinese)

［11］ 沈旭凯.开槽法测试混凝土工作应力试验研究［D］.杭州:浙江大学，2006.Shen Xukai.The testing and research on the working stress measurement of concrete by the grooving method［D］.Hangzhou:Zhejiang university，2006.(in Chinese)

［12］ 王柏生，沈旭凯，林湘祁.开槽法测试混凝土工作应力的试验研究［J］.浙江大学学报(工学版)，2010，44(9):1754-1759.Wang Baisheng，Shen Xukai，Lin Xiangqi.Experimental study on working stress measurement of concrete by grooving method［J］.Journal of Zhejiang University(Engineering Science)，2010，44(9):1754-1759.(in Chinese)

［13］ 徐芝纶.弹性力学［M］.北京:高等教育出版社，1990.Xu Zhilun.Elastic mechanics［M］.Beijing:Highher Education Press，1990.(in Chinese)

［14］ 殷之霖，张誉，王振东.抗扭［M］.北京:中国铁道出版社，1990.Yin Zhilin，Zhang Yu，Wang Zhendong.Torsion［M］.Beijing:China Railway Press，1990.(in Chinese)

［15］ 陆明万，罗雪福.弹性理论基础［M］.北京:清华大学出版社，2001.Lu Mingwan，Luo Xuefu.Basic theory of elasticity［M］.Beijing:Tsinghua University Press，2001.(in Chinese)